Primary Maths Dictionary for Kids and Parents: A Guide To The Mathematical Terms Used In KS1 And KS2

Bet you never thought you’d need a maths dictionary for kids when your child started school! But as parents the maths words that your children have to contend with in school may be quite different from those you learnt and used in your primary education.

Throughout their time studying maths in primary school, both at KS1 and KS2, your child will be introduced a huge number of maths vocabulary, much of which may seem baffling – both to them and to you.

This primary school maths dictionary for kids and their parents is, we hope, the solution to any questions and confusion. It’s an A to Z maths glossary of meanings for all those words and phrases you’re not sure about from acute angles through to word problems.

It is by no means a comprehensive list of every mathematical term that could come up throughout your child’s school life (as that would be too overwhelming), but it includes the key ones they will need to form solid foundations in primary maths and onto secondary school and GCSE maths.

The importance of spoken mathematical language

When children struggle to articulate their thoughts, it is usually a sign that they do not understand the topic they in discussing in great depth and this can often be the case in maths.

This quote taken from the Department for Education reflects the importance of mathematical language amongst children:

“The national curriculum for mathematics reflects the importance of spoken language in pupils’ development across the whole curriculum – cognitively, socially and linguistically. The quality and variety of language that pupils hear and speak are key factors in developing their mathematical vocabulary and presenting a mathematical justification, argument or proof.”

National Curriculum in England, Department for Education, 2013

When children use spoken language in maths in a productive manner, it allows them to evaluate their learning, support their peers, challenge the status quo, justify their own answers and most importantly ask questions!

Using a wide range of maths vocabulary can help children to make links across not only different areas of maths, but also throughout real life situations. One example of this could be in the supermarket, when they would realise, thanks to their range of vocabulary, that a 50% off sticker means the same as half price.

Mathematical vocabulary appears in more places than you would think, and that is why it is very important that your child is confident in their ability to articulate about all things mathematical!

How you can encourage a wider range of mathematical language in your child

There are a number of ways you can encourage your child to enhance their mathematical vocabulary and they include:

• Getting them to read and test themselves with our primary school maths glossary;
• Asking them open ended questions. No more “Do you know the answer to this question?” and more “What do you think the answer to this question is?”;
• Playing some word based maths games;
• Reading outside the world of maths as many children’s books will incorporate elements of maths in a fun and engaging way. ‘One is a Snail, Ten is a Crab’ is a great example of this.

---

#

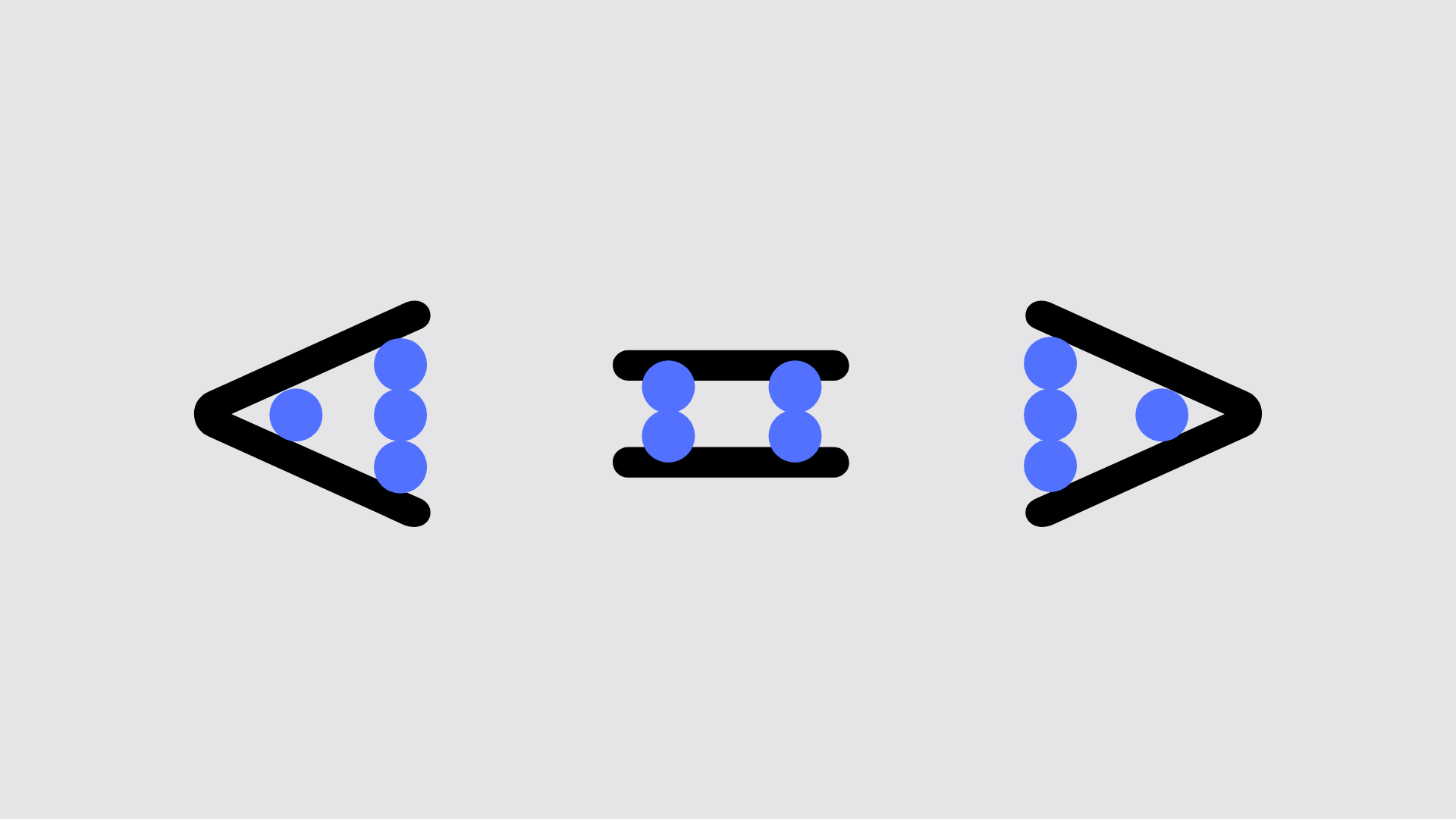
< and >

< and > are symbols representing one number being ‘greater than’ or ‘less than’ another.

For example 16 > 8 or 8 < 16 says that 16 is greater than 8 and 8 is less than 16.

12-hour and 24-hour clock

The 12-hour clock goes from 1 am in the morning to 12 noon and from 1 pm in the afternoon to 12 midnight. This is known as ‘analogue’ time.

The 24-hour clock goes from 00:00 (midnight) to 23:59 (one minute to midnight). This is known as ‘digital’ time.

Read more: What is the 12 hour and 24 hour clock

2D shapes

A 2D shape is any flat or ‘two-dimensional’ shape, such as a square, circle or triangle.

3D shapes

A 3D shape is ‘three-dimensional’ and has volume, for an example a cube (cardboard box), pyramid or cylinder (tube).

Read more: 2D shapes, 3D shapes and properties of shapes

A

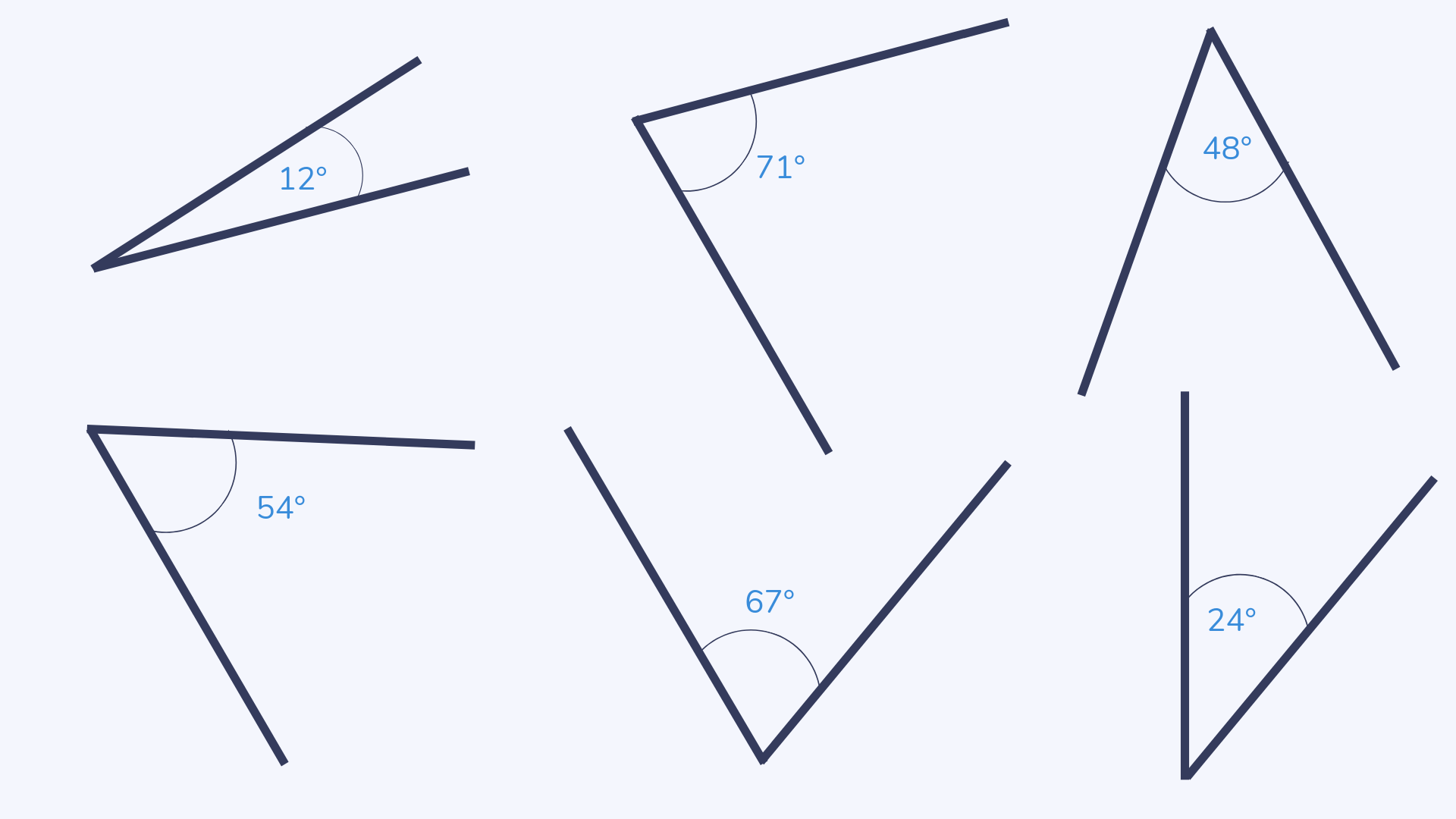
Acute angle

An acute angle is any angle less than 90°.

Algebra

In algebra, letters and symbols are used to represent numbers in equations or formulae.

For example, if w = 3, what is 6w + 7?

Analogue and digital clocks

An analogue clock is a clock with the numbers 1 to 12 around the outside and two hands, one short hand that represents hours and one long hand that represents minutes.

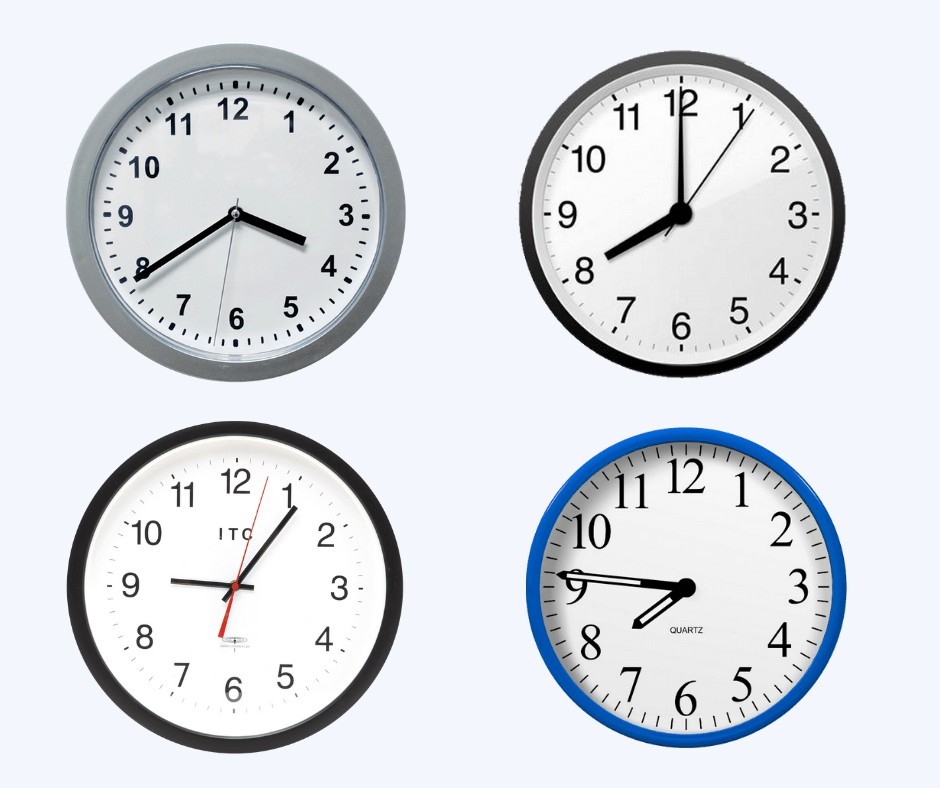
A digital clock uses 24-hour time and always has four digits.

For example, 15:30 is half-past three in the afternoon on a digital clock.

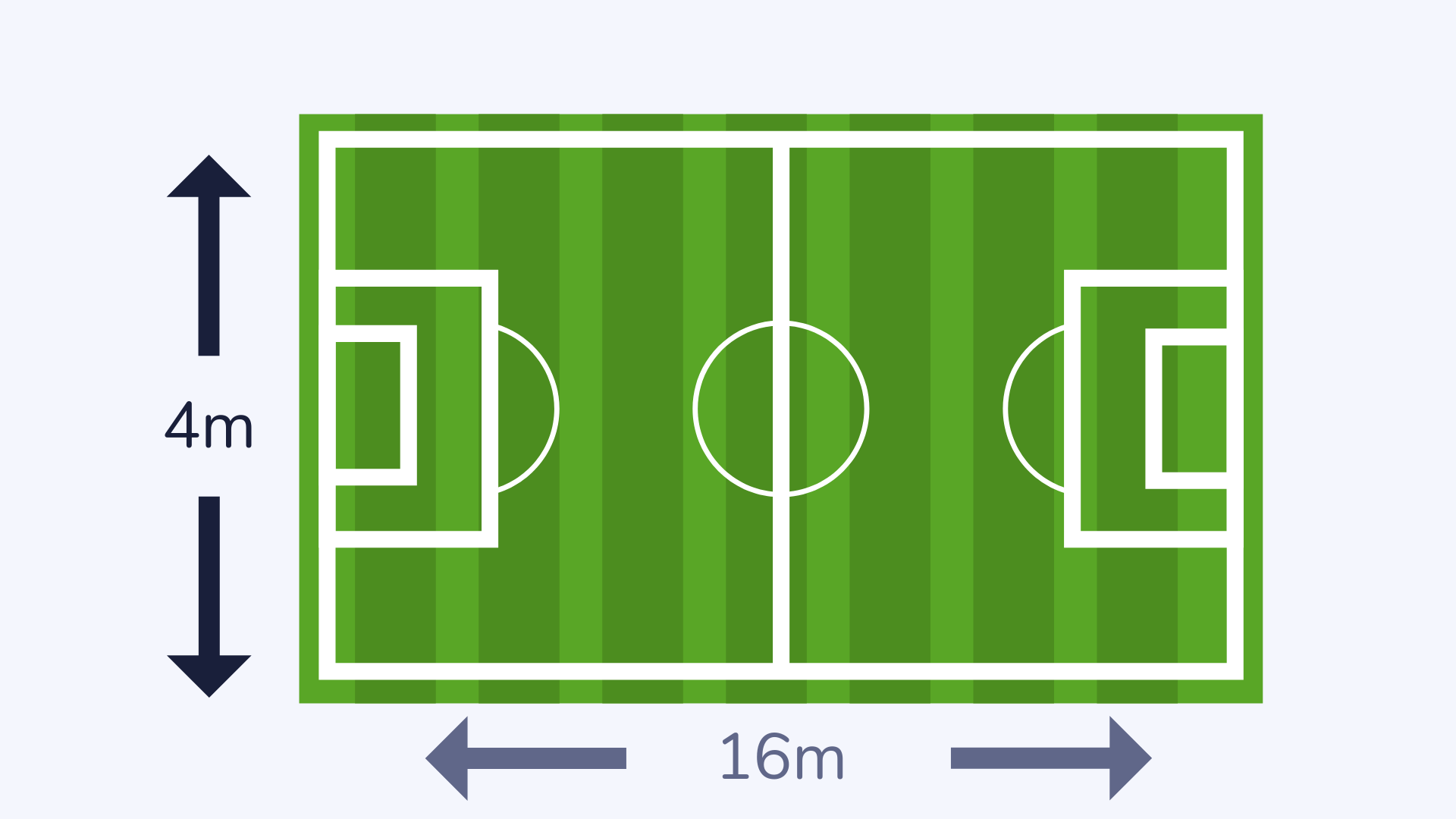
Area

The area of a shape, surface, piece of land etc. means the amount of space it takes up.

For example, a rectangular football field has an area of 64m² or 64 squared metres.

Array

An array is a pictorial representation of a calculation, using rows of dots, to help children understand multiplication and times tables.

Arrow cards

Arrow cards are a maths tool useful for explaining place value and how to partition numbers (separate them into ones, tens, hundreds etc).

Ascending order

To ascend means to go up, so numbers given in ascending order are going from smallest to largest.

For example, 1, 2, 3, 4, 5, 6 are numbers in ascending order.

Associative property

The associative property says that when we add or multiply numbers, it doesn’t matter how we group them (which we calculate first).

For example, (7 + 5) + 3 = 7 + (5 + 3) or (4 x 5) x 2 = 4 x (5 x 2)

Average

The average of a set of numbers is found by adding all the numbers together and dividing by how many numbers there are.

For example, the average of 12, 10, 8 and 6 is 9 because (12 + 10 + 8 + 6 = 36 ÷ 4).

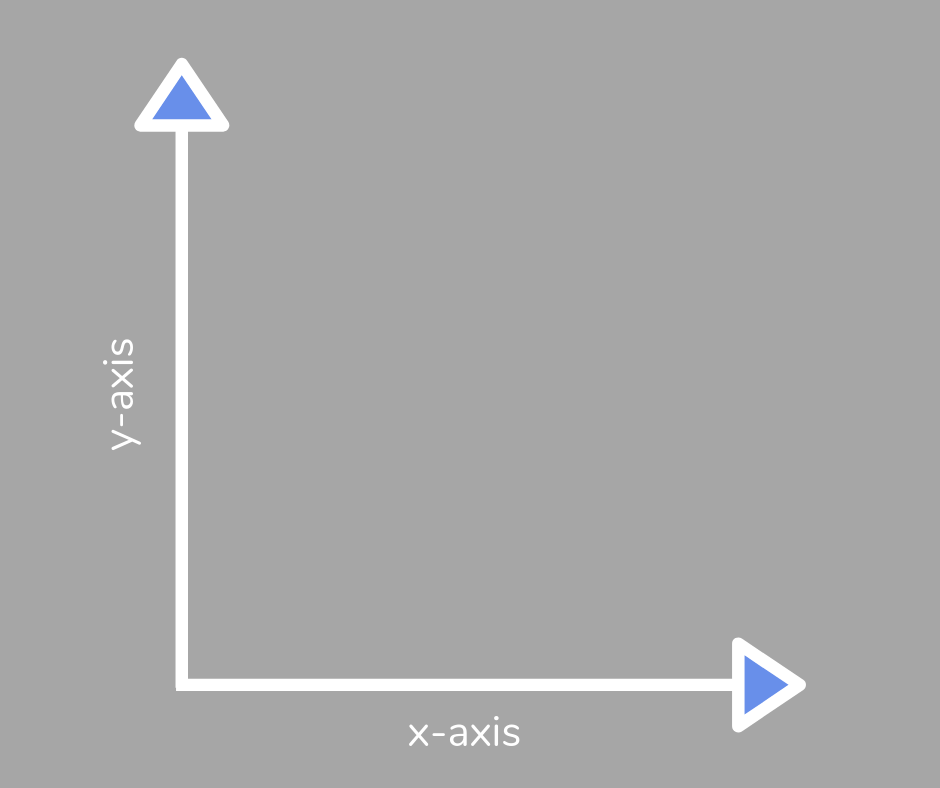
Axes

The axes of a graph or chart are the horizontal and vertical lines that create it, often known as the x-axis and y-axis.

B

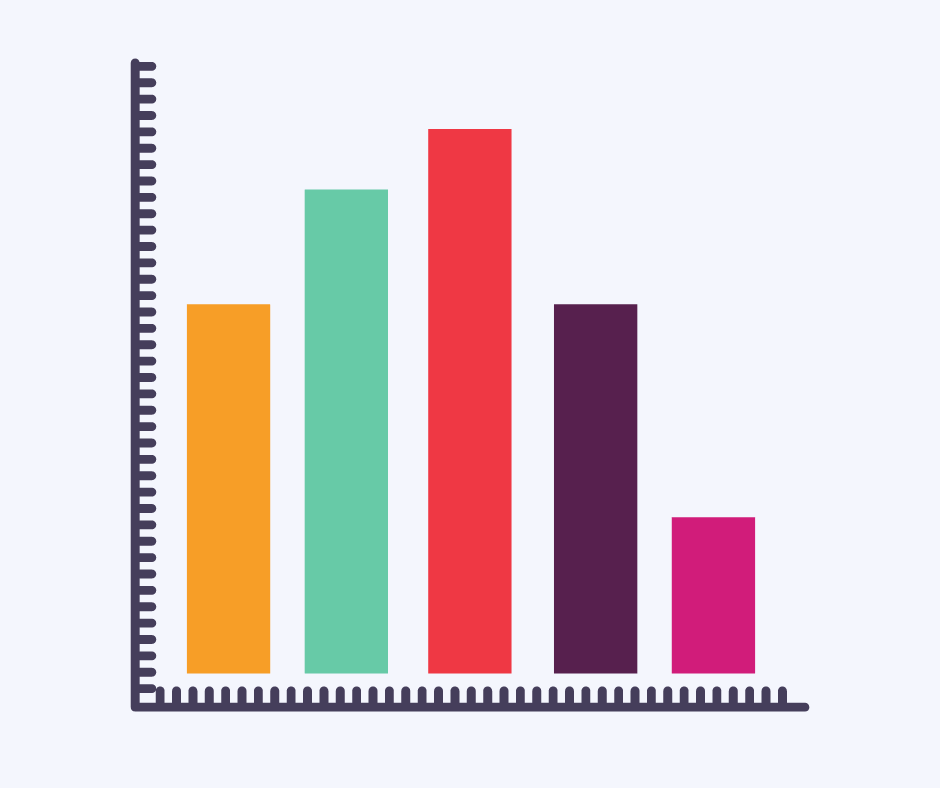
Bar chart

A bar chart is a form of graph that displays information using rectangular bars of different heights, according to their numerical value.

Bar model

A bar model is a method that uses diagrams of rectangular bars to represent maths problems in a visual way, making them easier for children to see which operation to use to work out a calculation. Younger children may use cubes to physically represent this.

Read more: What is a bar model

Block graph

A block graph is a simpler version of a bar chart, but using blocks to represent the data, with each block worth 1 unit.

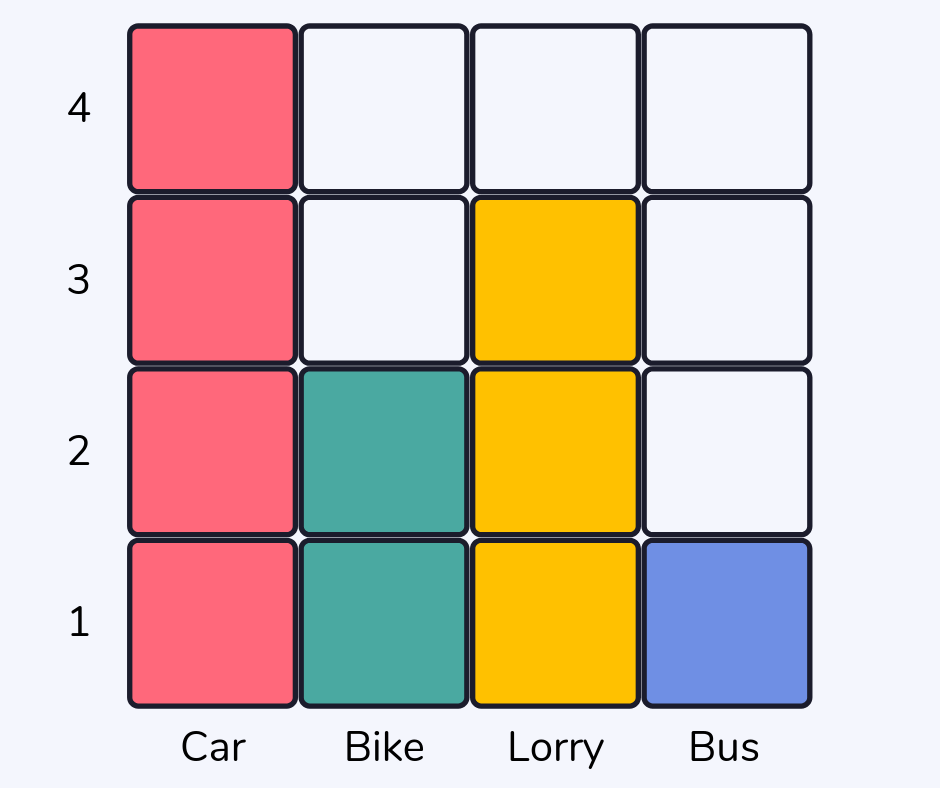
BODMAS

BODMAS is a rule for the order to work out calculations with mixed operations. It stands for Brackets, Orders, Division, Multiplication, Addition, Subtraction and is sometimes seen as BIDMAS (Brackets, Indices, Division, Multiplication, Addition, Subtraction) or even PEMDAS (Parentheses, Exponents, Multiplication/Division, Addition/Subtraction)

Read more: What is BODMAS?

Bridging through 10

Bridging through 10 is a way of adding numbers greater than 10 in your head.

For example, to add 8 + 7, you add 2 (from the 7) to get 10, then add the remaining 5 to get 15.

Bus stop method

The ‘bus stop’ method or short division is a way of dividing numbers with two or more digits by one or two digit numbers.

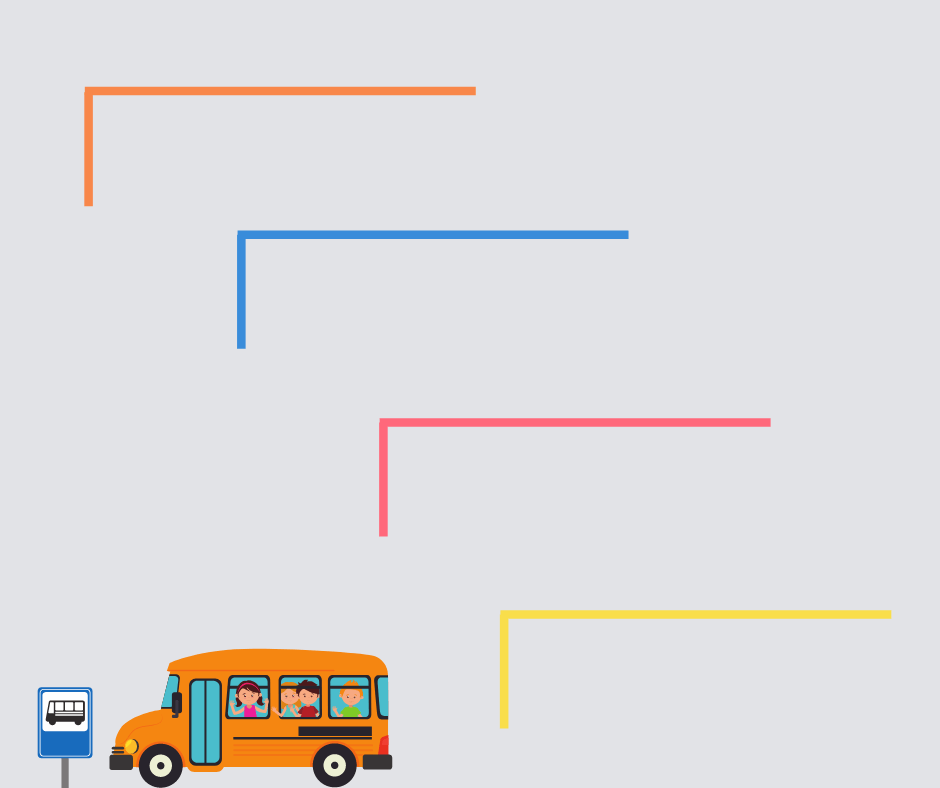
Read more: What is bus stop method

C

Capacity

The capacity of a container is how much that container can hold, measured using units such as litres, millilitres, pints etc.

Cardinal numbers

A cardinal number tells you how many of something there are; they refer to a set of objects. For example, there are three marbles in my hand. This is in contrast to an ordinal number which tells you the position of something in a list, for example first, second, third.

Carroll diagram

A Carroll diagram is a way of organising information and grouping according to what criteria it fits into.

For example, which shape has 6 sides and 1 line of symmetry?

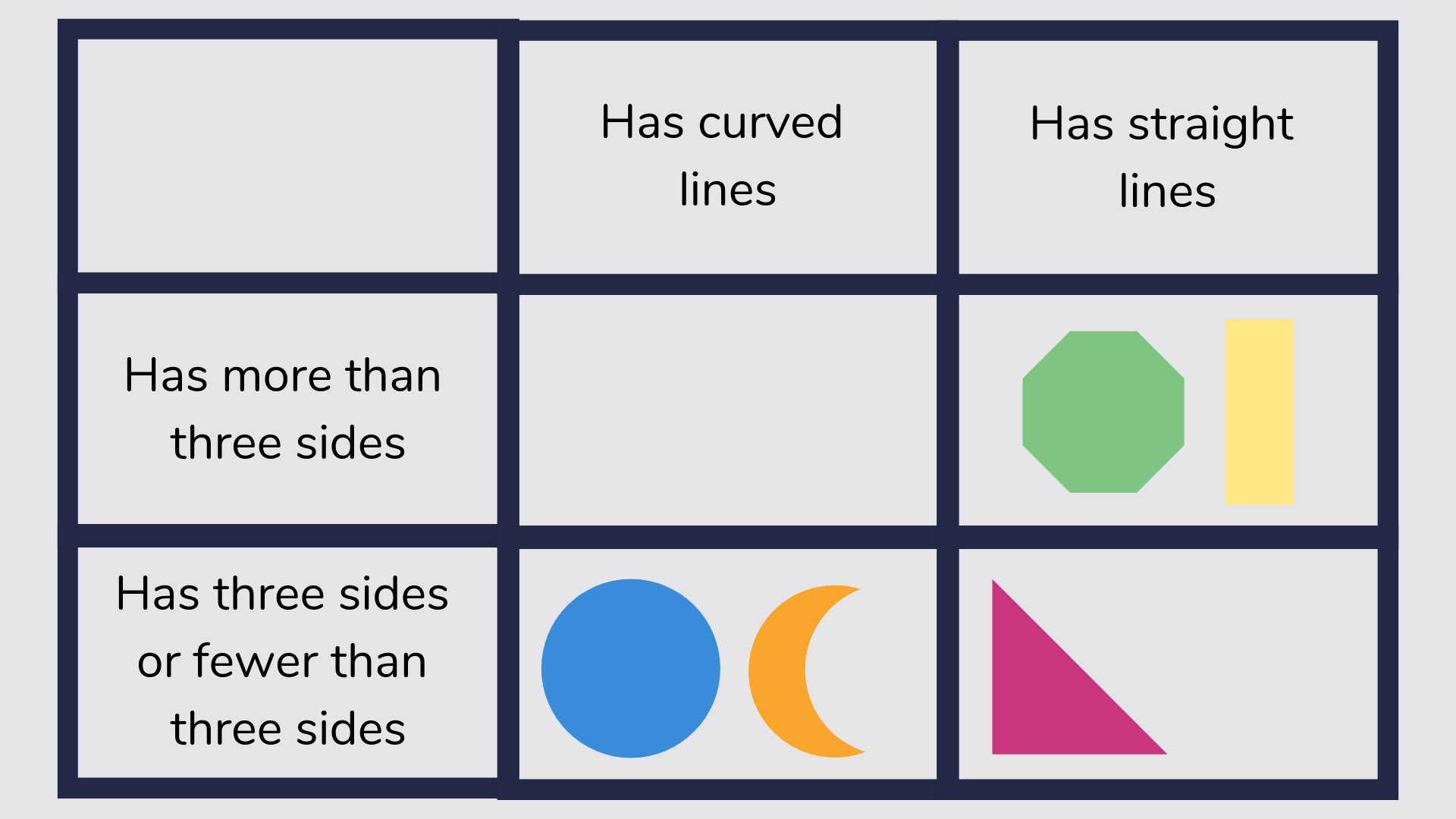
Read more: What Is A Carroll Diagram?

Circle

A circle is a simple curved 2D shape, with 1 edge, no corners and infinite lines of symmetry.

Circumference

The circumference is the length around the edge of a circle.

Clockwise and anti-clockwise

To move in a clockwise direction means moving in the same direction as the hands on a clock. If something moves in the opposite direction to the hands of a clock, it is moving in an anticlockwise direction.

Coordinates

The coordinates of a shape or object refer to where on a map or graph they are, by looking at the two axes and recording the numbers they are at. These can be taught with the phrase “along the corridor and up/down the stairs” to refer to looking at the x-axis first then looking at the y-axis.

Read more: What are coordinates?

Column method

The column method is way to solve addition and subtraction calculations, that sometimes involve ‘exchanging’ amounts from one column to the next (which in the past has been called ‘carrying’ and ‘borrowing’). The numbers are written on top of each other, with the correct digits in each column (e.g. hundreds, tens, ones).

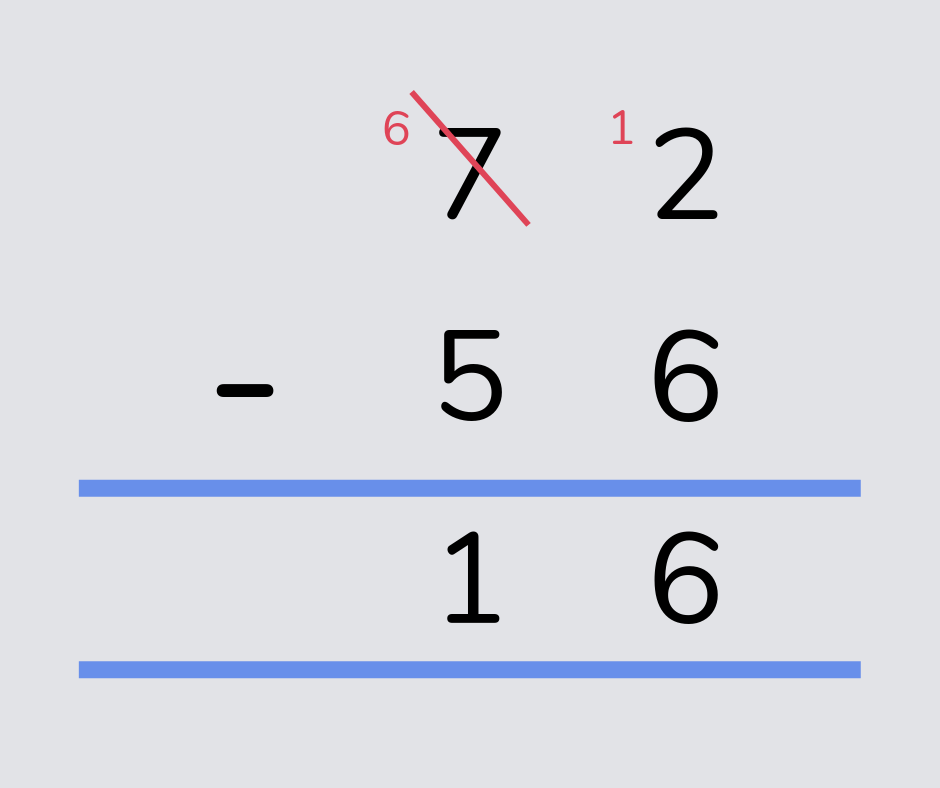
Read more:

• What is column subtraction?
• What is column addition?

Commutative property

The commutative property states that addition and multiplication calculations can be carried out with the numbers in any order, whereas for subtraction and division, the numbers must be in a particular order.

For example, 8 x 9 = 72 or 9 x 8 = 72

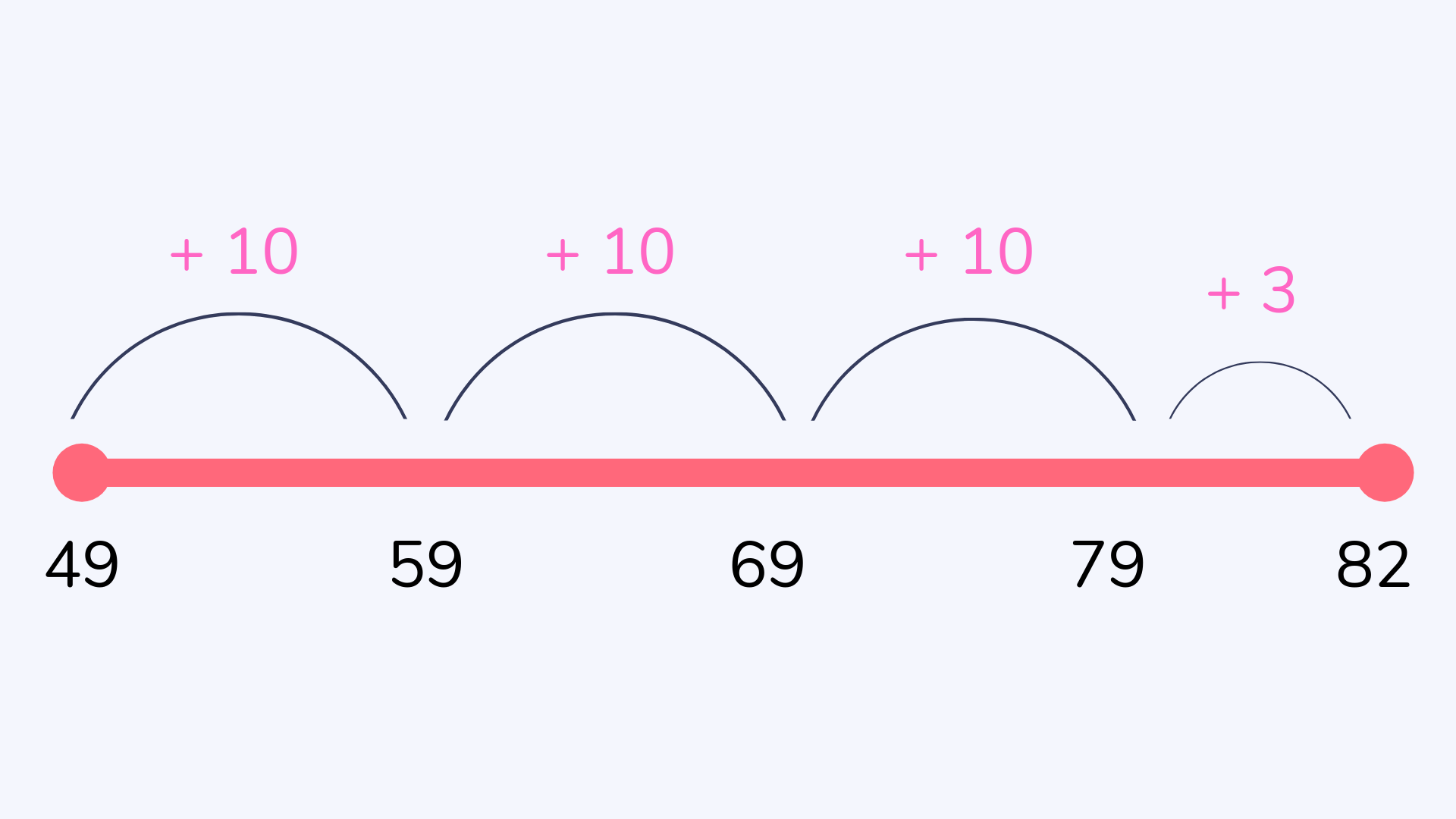
Complementary addition (subtraction on a number line or the jump strategy)

Complementary addition is a method for subtraction that involves using a number line to jump from the smaller number to the bigger number and counting the number of jumps. This method is useful in KS1 for teaching children to ‘find the difference’ between two numbers.

Concrete, Pictorial, Abstract approach (CPA)

The concrete, pictorial, abstract approach is a way of teaching mathematical concepts and theories in various stages, in order to help children fully understand and master what they are learning.
The concrete stage involves using items, models and objects, giving children a chance to be ‘hands-on’.

For example, children may solve a problem adding groups of toys together using real toys, or they may manipulate buttons, Lego, etc when working out fractions of amounts. At school, there are a variety of concrete resources specially designed for maths, such as place value counters, dienes, rekenreks, and numicon.

The pictorial stage uses visual representations of concrete objects to model problems, encouraging children to make connections between the physical object and the picture that represents the object.

For example, children may use drawing of toys to solve a problem adding toys.

The abstract stage uses symbols, such as numbers or mathematical symbols (+, -, x, =) to model problems. Children will need to master the concrete and pictorial stages before moving onto the abstract stage.

Converting into same units

When you convert measurements into the same units, you understand that the same length, weight or capacity can be shown in different units of measurement.

For example, a bottle of water can be measured in litres or millilitres and there are 1000ml in 1L.

Cube numbers

A cube number is the result of when a number is multiplied by itself three times. When writing cube numbers, we write a small three above the number, e.g. 3 x 3 x 3 or 3³ = 27

Read more: What are cube numbers?

D

Data handling

Data handling is another term for statistics, meaning how we collect, display and interpret data or information, such as the most popular flavour of ice cream in a class, using tables, tally charts, pictograms, block diagrams, bar charts, line graphs and pie charts.

Decimal

A decimal is a number that contains tenths, hundredths, thousandths etc, with a decimal point between the ones and tenths. Money is often used to teach decimals.

For example, 3.4, 2.18, £56.99

If you are interested in other ways to teach your child about money, take a look at our blog. 

Degrees

We use degrees as the unit of measurement for measuring angles, usually symbolised with a small circle above the number. For example, a right angle is 90° (90 degrees).

Denominator

A denominator is the name for the bottom number in a fraction. For example, in the fraction 4/10, 10 is the denominator.

Descending order

Descending order means to go from the largest number to the smallest and is the opposite of ascending order.

For example, 90, 80, 70, 60, 50 are numbers in descending order.

Diagonal

A diagonal is a line joining two opposite corners of a square, rectangle or other shape.

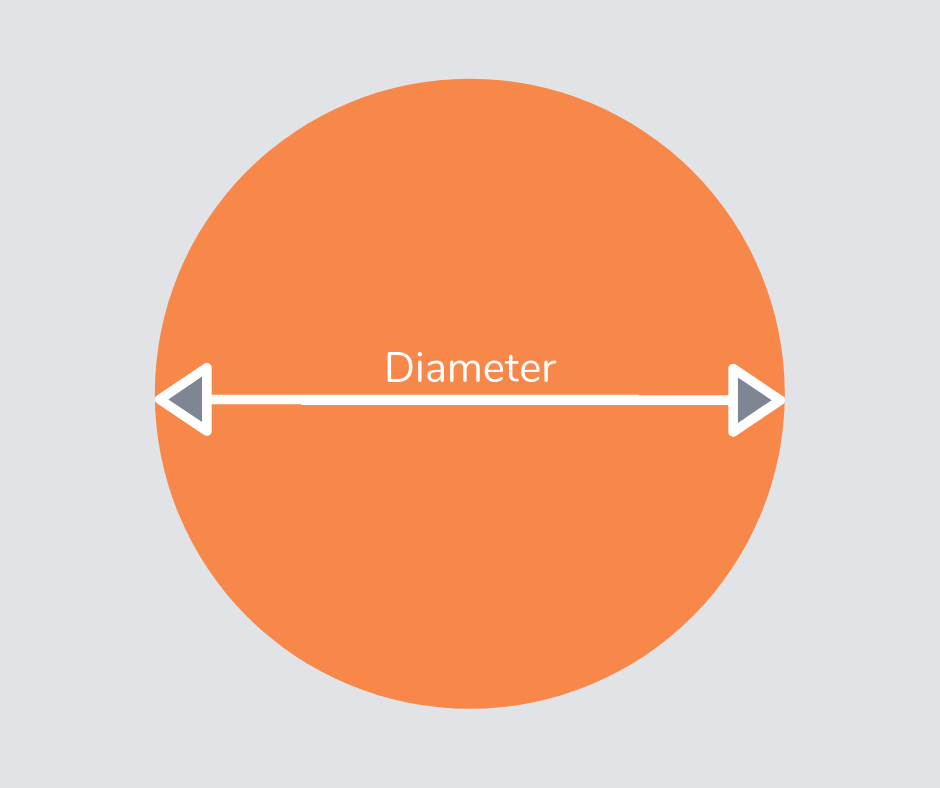
Diameter

The diameter is a straight line going from one side of a circle to another, through the centre.

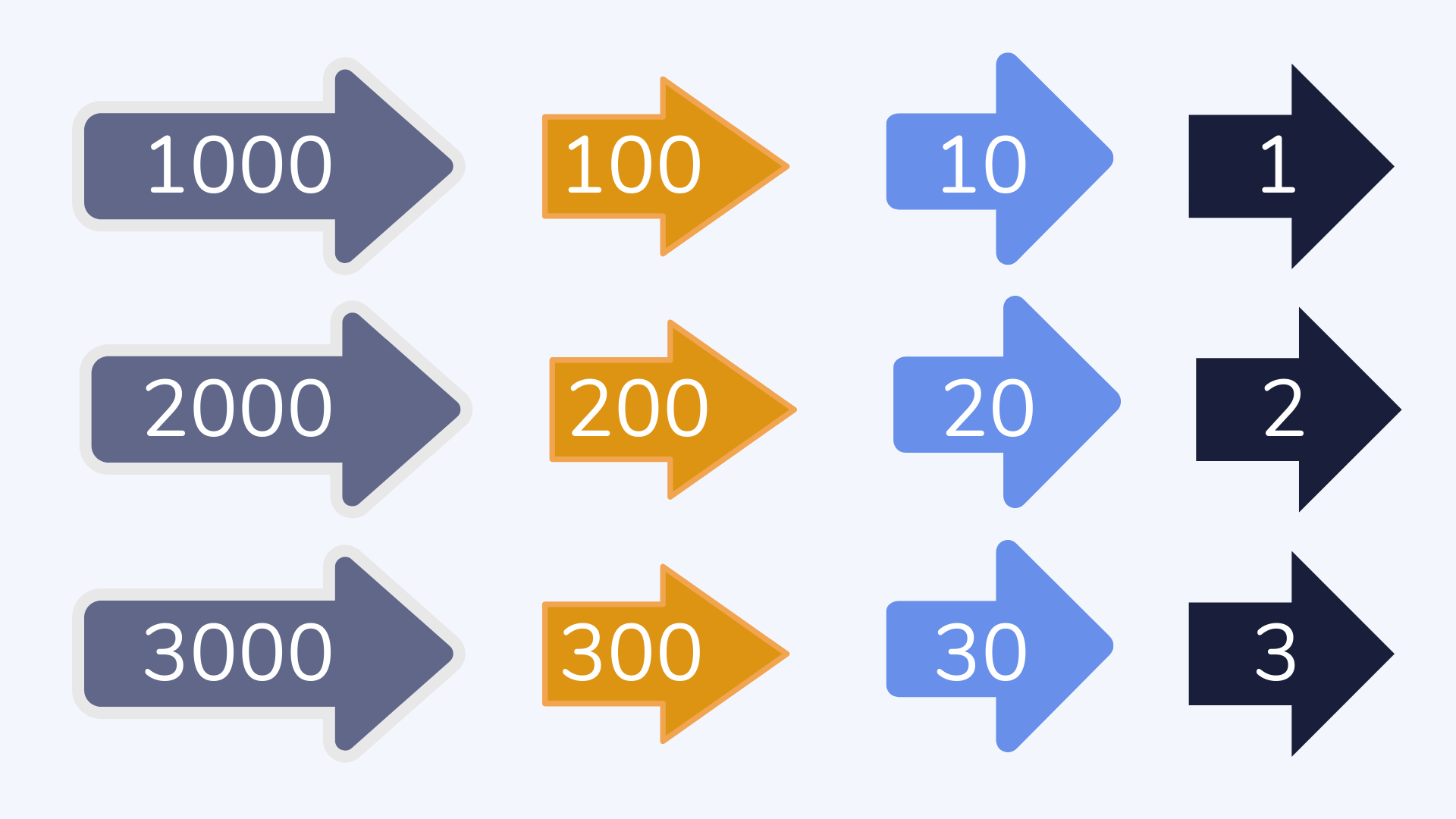
Dienes

Dienes are coloured plastic or wooden blocks that are used to represent numbers. They are usually used to represent 1000, 100, 10 and 1. Dienes allow teachers and students to represent numbers visually.

Distributive property

The distributive property states that multiplying a number by a group of numbers added together is the same as doing each multiplication separately.

For example, 5 x (2 x 6) = 5 x 2 + 5 x 6

Dividend

The dividend is the number that you are about to share out.

Divisor

The divisor is the number of times you need to share out your dividend.

Division facts

Division facts are the division calculations related to times tables.

For example, 50 ÷ 5 = 10 and 25 ÷ 5 = 5 are division facts related to the 5 times table.

Read more: Division For Kids: Short and Long Division Explained

E

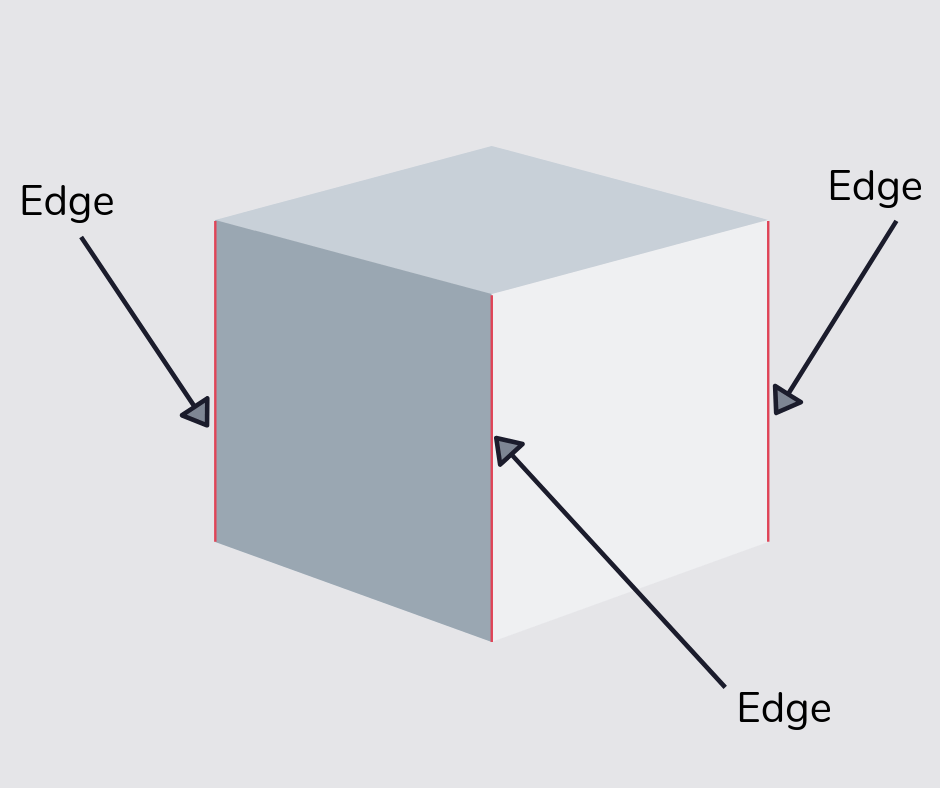
Edge

An edge is the name for lines created when two faces in a 3D shape meet.

Equation

An equation is another name for a number sentence where both sides equal the other.

For example, 12 – 5 = 3 + 4

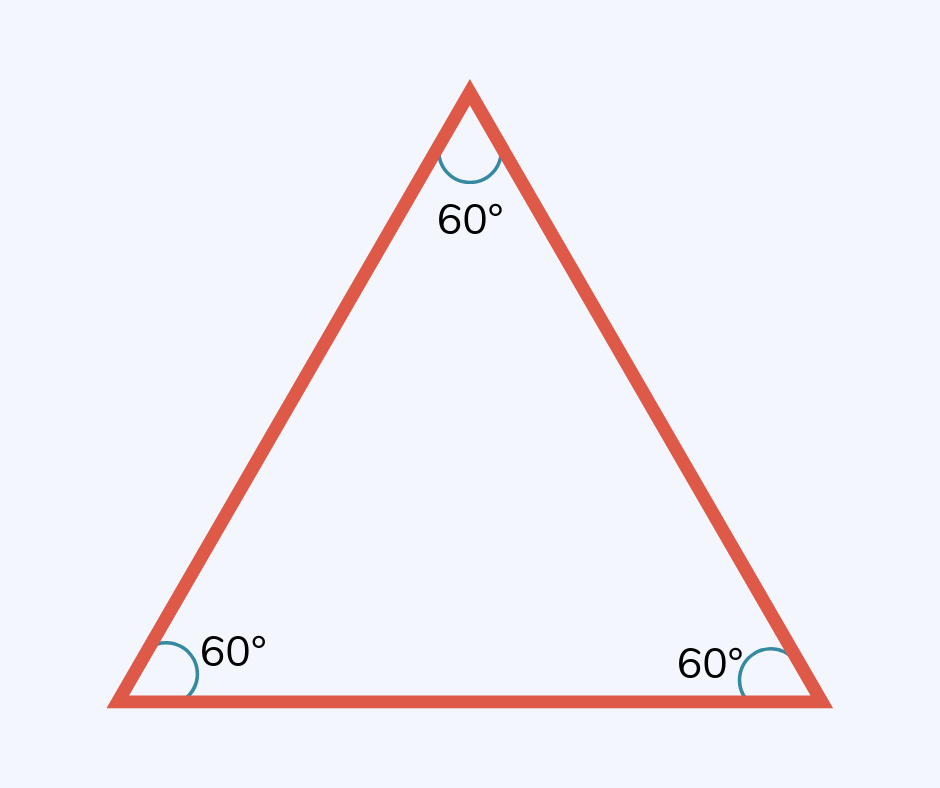
Equilateral Triangle

An equilateral triangle is a triangle with three equal sides and three equal angles.

Equivalent fractions

An equivalent fraction is one that is equal in terms of size to another, but written using different numbers. For example, ½ is equivalent to 4/8 and 7/14.

Read more: What are equivalent fractions?

Estimate

To estimate is to make a clever guess to the answer of a question, by roughly calculating the value. For example, children estimated the length of the playground to be 100 metres.

Expanded notation

Expanded notation means to write a number showing the value of each digit, with each digit being multiplied by its matching place value (ones, tens, hundreds etc).

For example, 352 = 3 x 100 + 5 x 10 + 2 x 1.

F

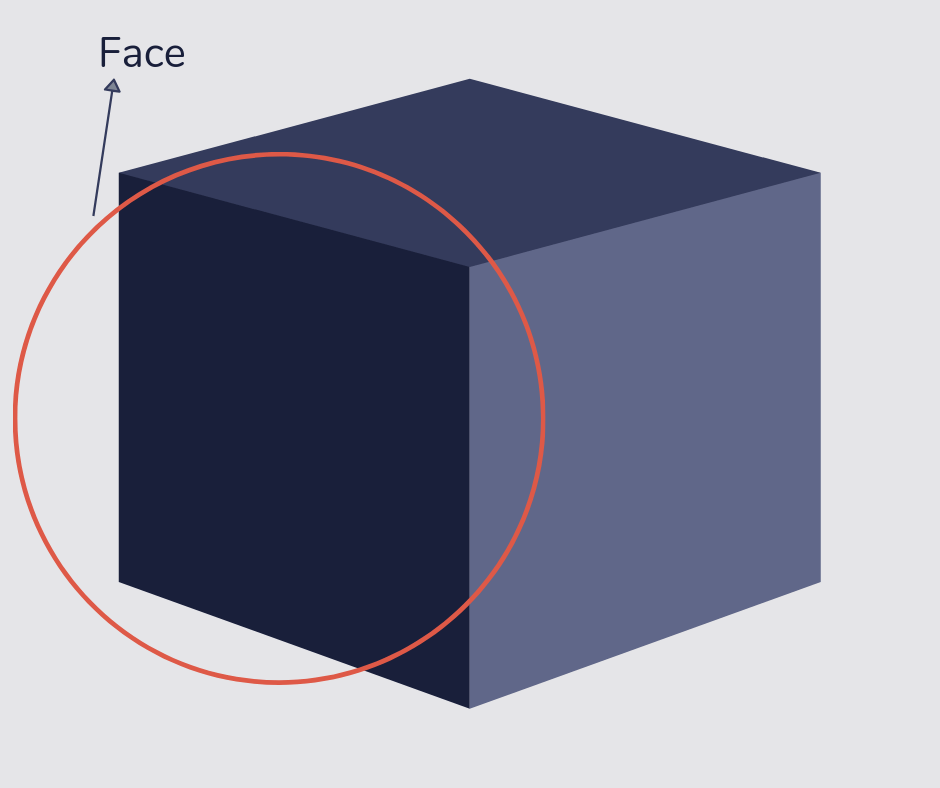
Face

A face is the flat part of a 3D shape.

Factor

A factor is a number that can divide exactly into another number.

For example, 2, 3, 4 and 6 are all factors of 12, as 12 can be divided into them exactly.

Factors and multiples are usually taught together and children often get the two confused. Read more about the difference between factors and multiples.

Finding the difference between two numbers

Finding the difference between two numbers is the same as subtracting a smaller number from a larger number. This method is usually taught using a number line, counting the jumps from one number to another.

Formula

A formula is a group of numbers and maths symbols that show how to work something out. At primary school, children will encounter formulae for finding the area and perimeter of 2D shapes and for finding the volume of 3D shapes.

G

Geometry

Geometry is the branch of maths where children learn about the properties, measurements, position and relationships of points, lines, angles and shapes.

Grid method

The grid method is a way for working out multiplication calculations, especially with larger numbers, involving partitioning the numbers, multiplying each part and adding the totals.

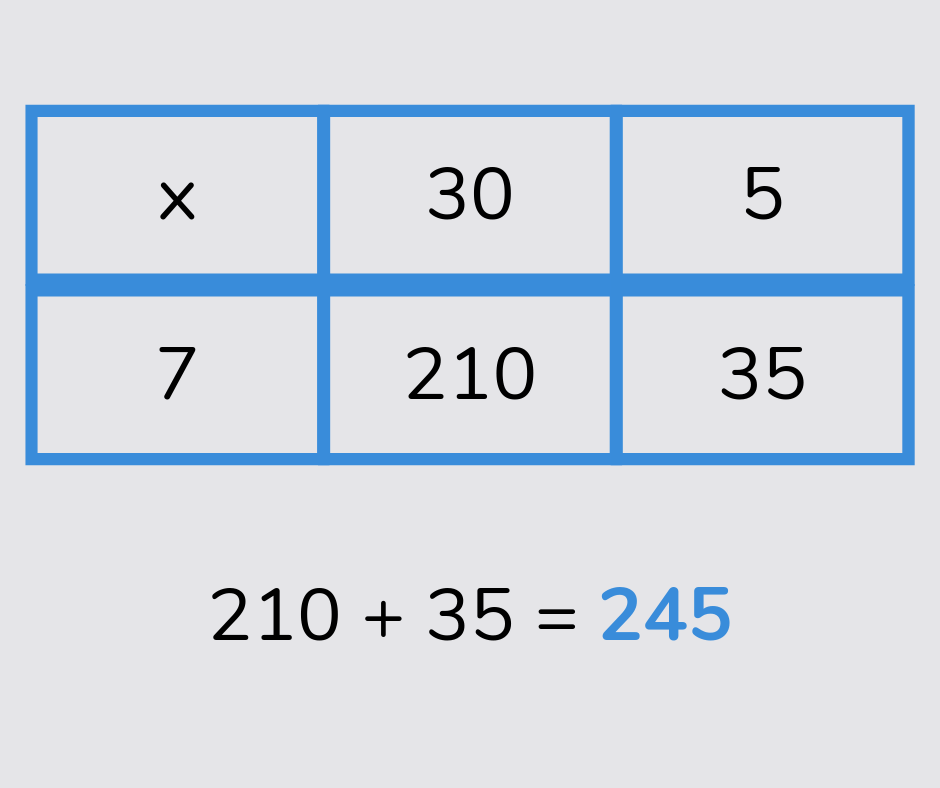
H

Highest common factor

The highest common factor is the largest whole number which is a factor of two or more numbers.

For example, 6 is the highest common factor of 12 and 18.

Read more: What is the highest common factor?

Horizontal

A horizontal line is one that goes from left to right and vice versa.

I

Imperial units

Imperial units are units of measurement that were used in the UK before the metric system was introduced. Children, especially from Year 5 on, will be taught how to convert from, for example, miles to kilometres.

Improper fraction

An improper fraction is one where the numerator is larger than the denominator and is also known as a ‘top-heavy’ fraction. For example, 11/4, 6/2 and 21/5 are all improper fractions.

Read more: What Is An Improper Fraction

Investigation

A mathematical investigation allows children to apply the skills and knowledge they’ve learnt to solve problems, which may have more than one way to work them out and more than one answer.

Integer

An integer is simply a whole number, either positive or negative. For example, 8, -23, 502 and -1000 are all integers.

Inverse operation

An inverse operation is another way of saying an opposite operation, which can often be used to check calculations are correct. For example, addition and subtraction are inverse operations, as are multiplication and division.

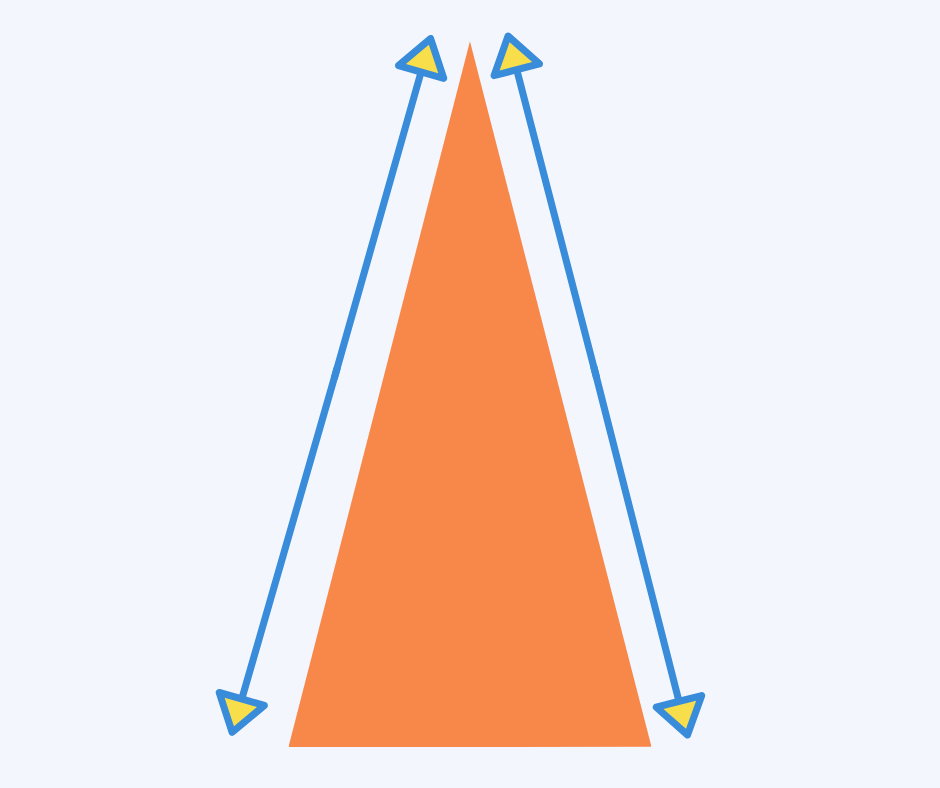
Isosceles triangle

An isosceles triangle is one with two equal sides and two equal angles.

J

Jump

A move made when practising addition or subtraction – forwards or backwards respectively – on a number line.

K

Kite

A quadrilateral (four-sided shape) with two pairs of adjacent (next-door) sides that are congruent (equal in length). The diagonals of a kite are perpendicular (meet at a right angle).

L

Length

The length of an object is how long or short something is, and is usually measured in metric units such as centimetres, metres and kilometres.

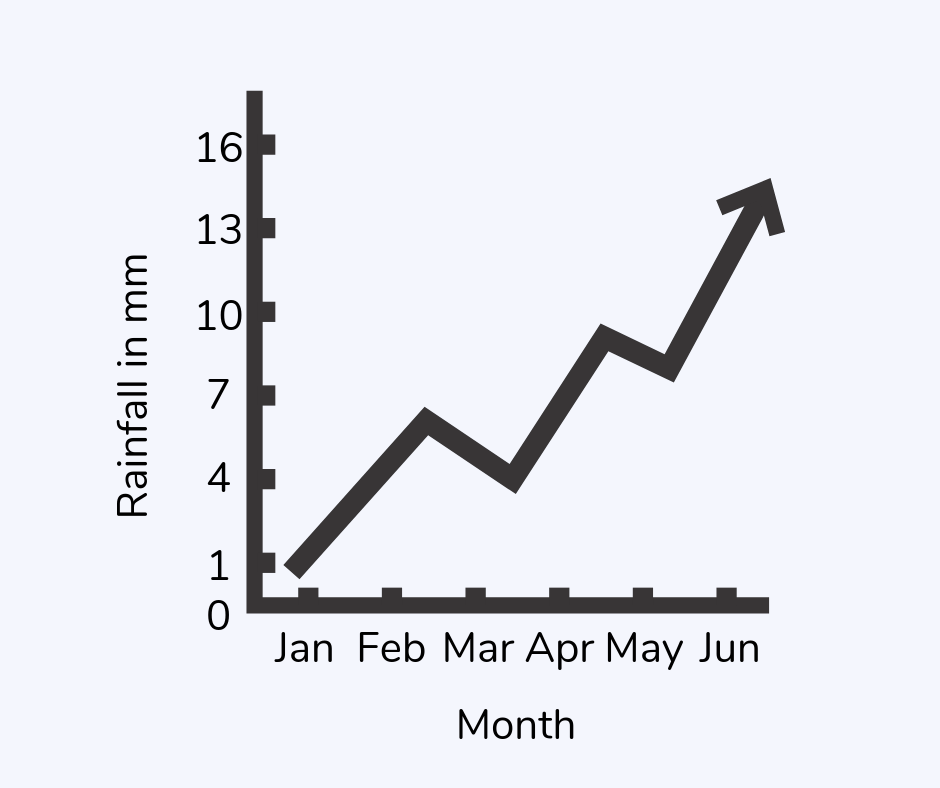
Line graph

A line graph is one where a line connects points, showing how values change over time.

For example, a line graph might show the amount of rainfall over six months.

Long division

Long division is a written method showing how to divide larger numbers (such as three or four-digit numbers) by other large numbers. Children will move onto long division in KS2, once they’ve mastered short division.

Long multiplication

Long multiplication, which is sometimes known as column multiplication, is a way of multiplying larger numbers together. Just like column addition and subtraction, the numbers are put in columns according to their place value. 

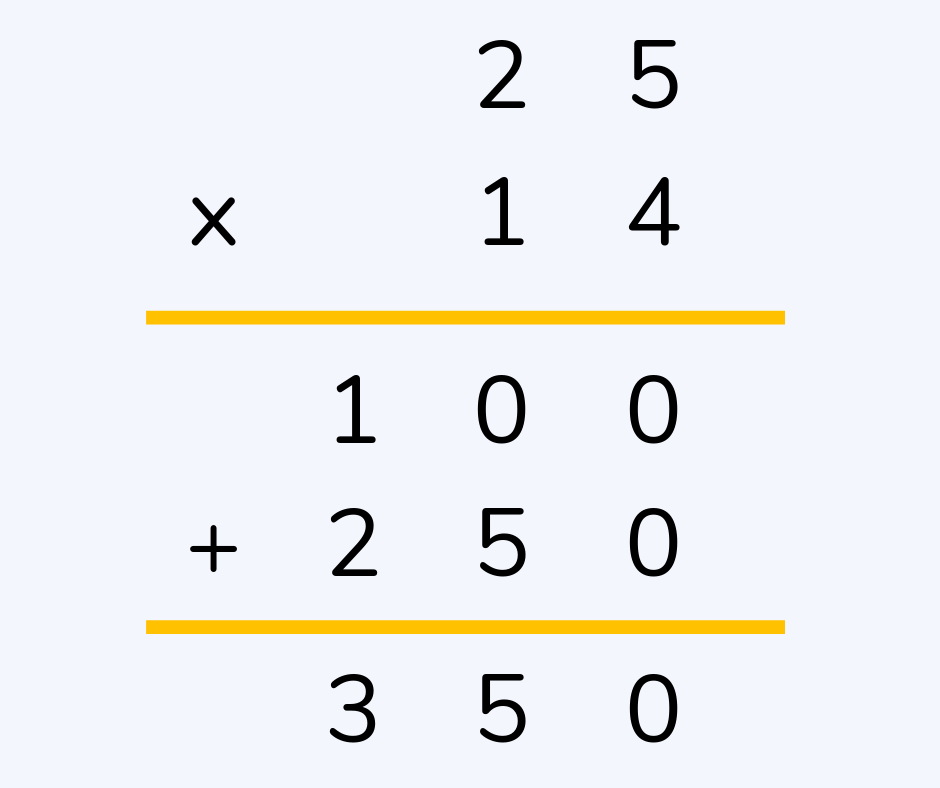
Read more: What is long multiplication?

Lowest common denominator

The lowest common denominator of two or more fractions is the smallest number that can be exactly divided by each denominator.

For example, 12 is the lowest common denominator of ½, ⅓ and ¼.

Lowest common multiple

The lowest common multiple is the smallest number which is a multiple of two or more numbers.

For example, the lowest common multiple of 4 and 5 is 20.

Read more: What is the lowest common multiple?

M

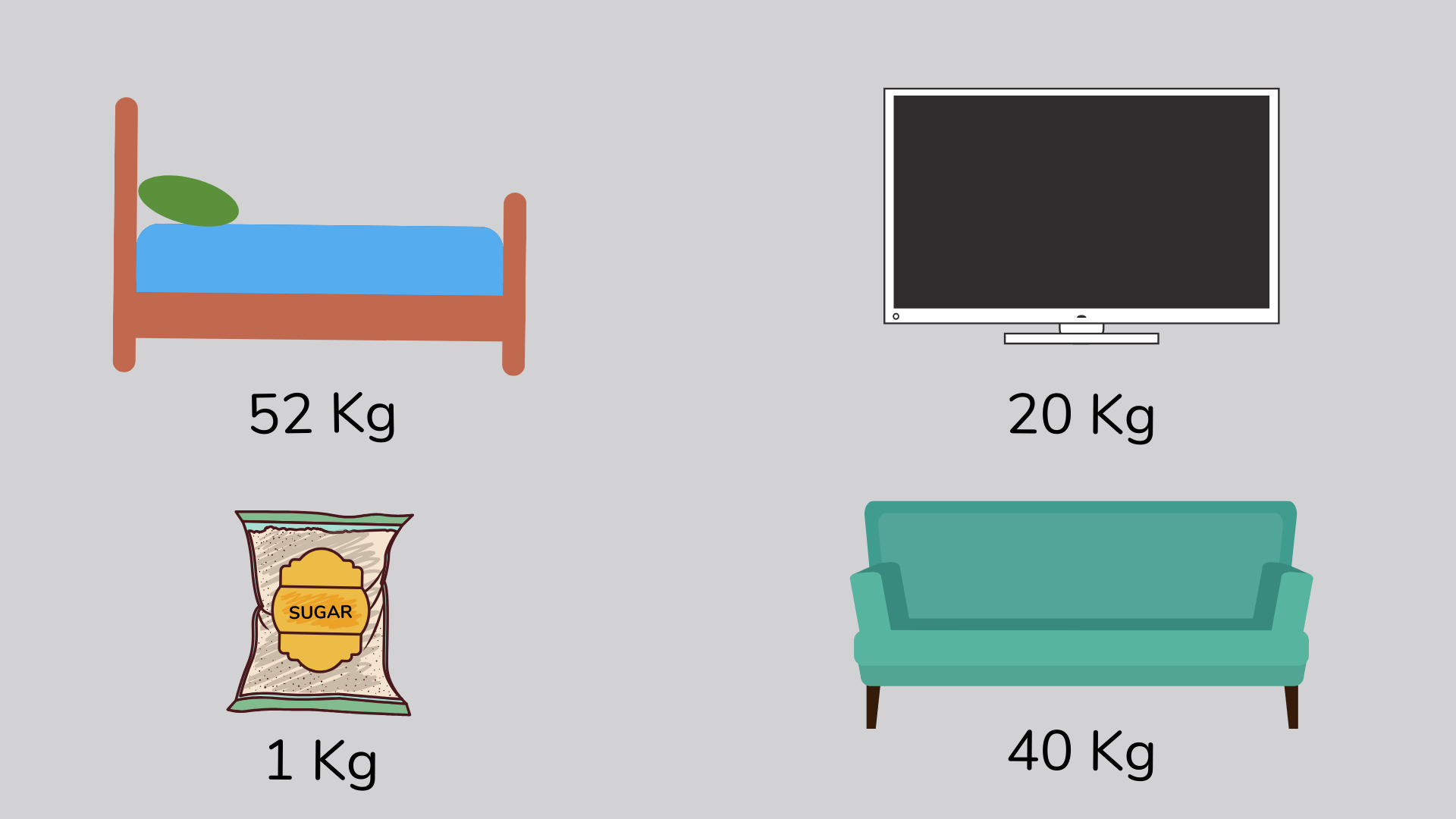
Mass

The mass of an object is how much it weighs and is usually measured in grams and kilograms.

For example, the mass of a bag of sugar is 1 kilogram.

Mastery

Having mastery in a maths topic means that children not only understand how to work out problems, but can also explain how they worked it out and apply their knowledge to more complicated word problems and investigations.

Mean

Mean is another word for average, and is found by adding a set of values and dividing the total by the number of values in the set.

For example, the mean of 2, 4, 5, 7 and 12 is 6 because (2 + 4 + 5 + 7 + 12 = 30 ÷ 5 = 6)

Read more: What Is Mean In Maths?

Median

The median of a set of numbers is the middle number in that list. The numbers in the list must first be sorted into ascending order, then children can find the median number.

For example, the median of 1, 2, 3, 4, 5, 6, 7 is 4.

Metacognition

Metacognition means to be aware of and analyse your thoughts and learning processes in order to make necessary changes to your learning behaviour. Techniques such as modelling problems and getting children to ask questions about their work are ways of improving their metacognition. 

Metric units

Metric units are units of measurement that are common around the world and are based on the metric system. For example, grams, centimetres, litres and seconds are all examples of metric units.

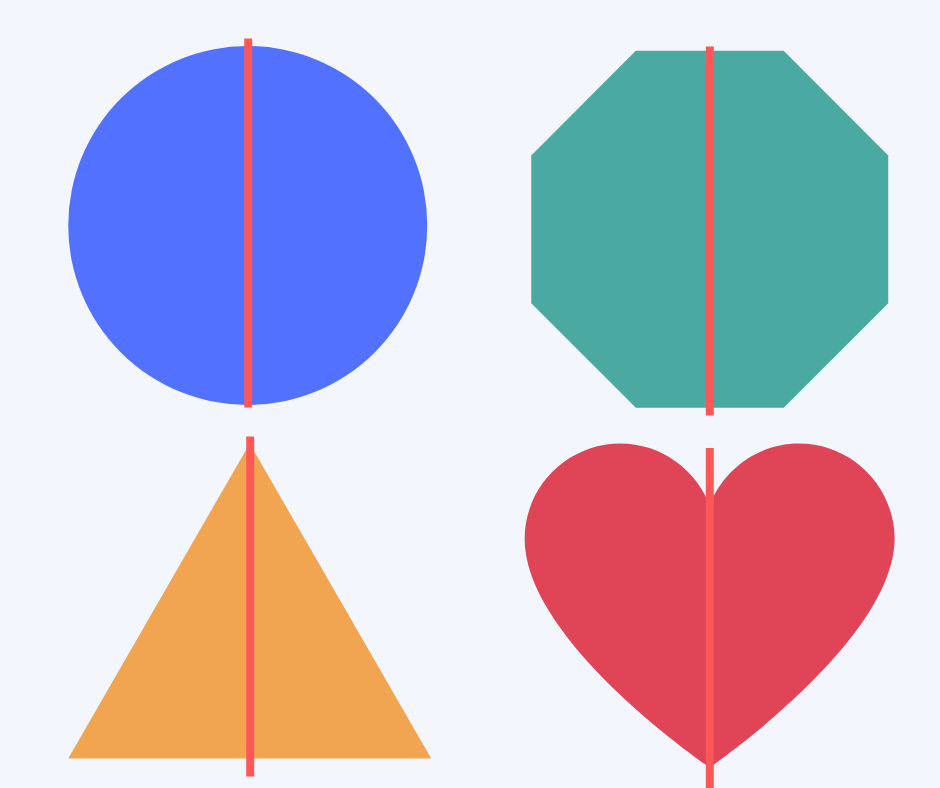
Mirror line

A mirror line is a line that can be drawn through the centre of a shape or picture to show that both sides are exactly the same.

Mixed number

A mixed number is one with both a whole number and a fraction. For example, 8 ⅔ and 5 10⁄12 are mixed numbers.

Read more: What is a Mixed Number?

Mode

The mode of a set of numbers is the one that appears most often. For example, the mode of 2, 3, 4, 5, 5, 6, 7 is 5.

Multiple

A multiple is the result of multiplying one integer by another. Multiples of a number are those in that numbers times table. For example, multiples of 7 include 14, 35, 49 and 84.

Multiple and factors are usually taught together and children often get confused. Read more about the difference between factors and multiples.

N

Negative numbers

A negative number is any number lower than 0 and is commonly taught using temperatures. For example, -2, -14, -67.

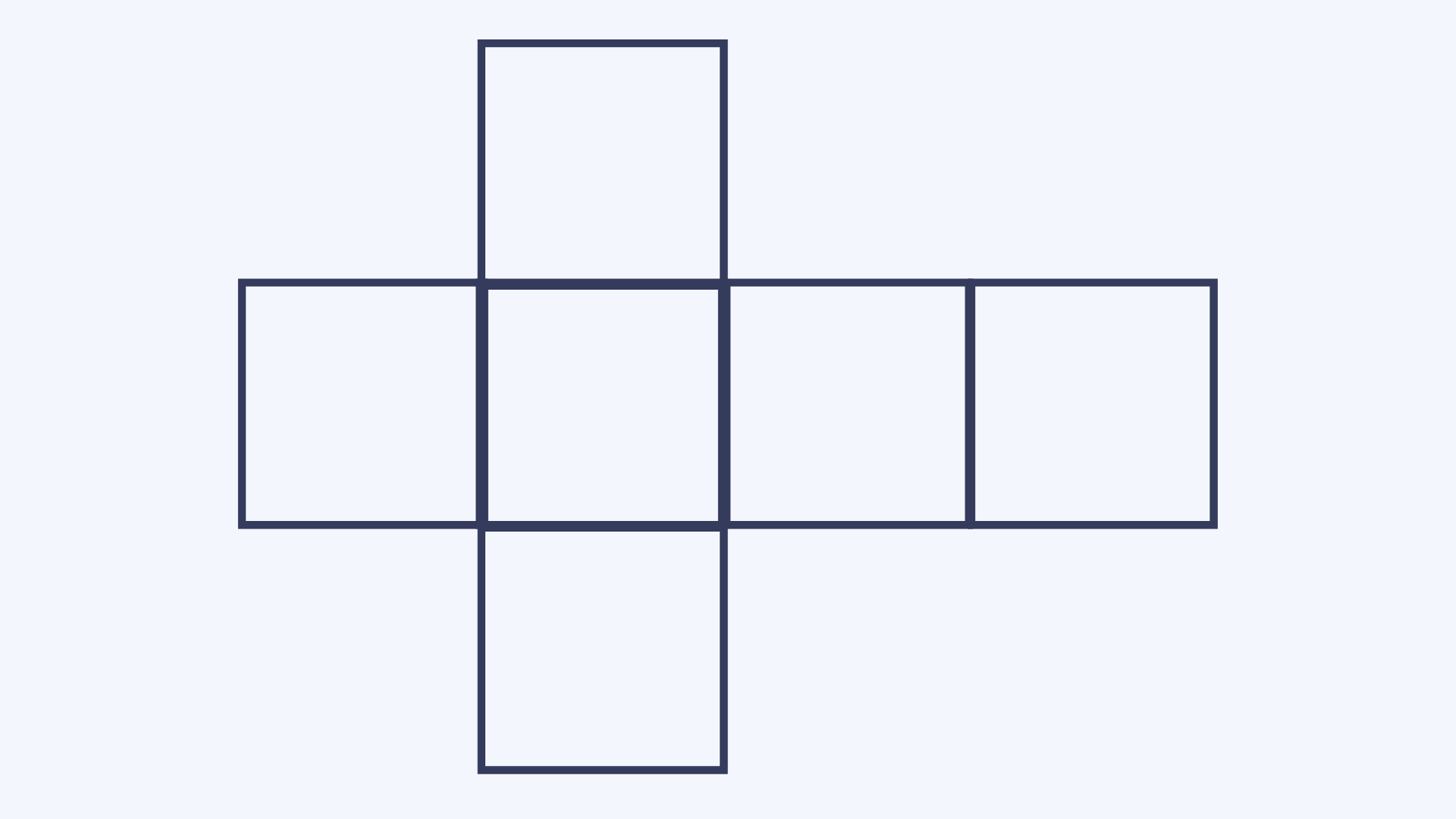
Net

A net is the flat outline of a 3D shape, before it is folded together.

Number bonds

Number bonds are pairs of numbers that add together to make a given number. For example, 2 + 8 and 4 + 6 are number bonds to 10, whereas 43 + 57 and 81 + 19 are number bonds to 100.

Read this: What are number bonds?

Number facts

Number facts are simple addition, subtraction, multiplication and division calculations that children should be able to mentally recall easily. For example, 50 + 50 = 100 or 2 x 2 = 4 are number facts.

Number line and number ladder

A number line is a horizontal line, with numbers going up the bottom of the line. The numbers will typically increase in size and the space between the numbers doesn’t usually matter. Number lines are especially used in Key Stage 1 to teach number bonds and adding using jumping.

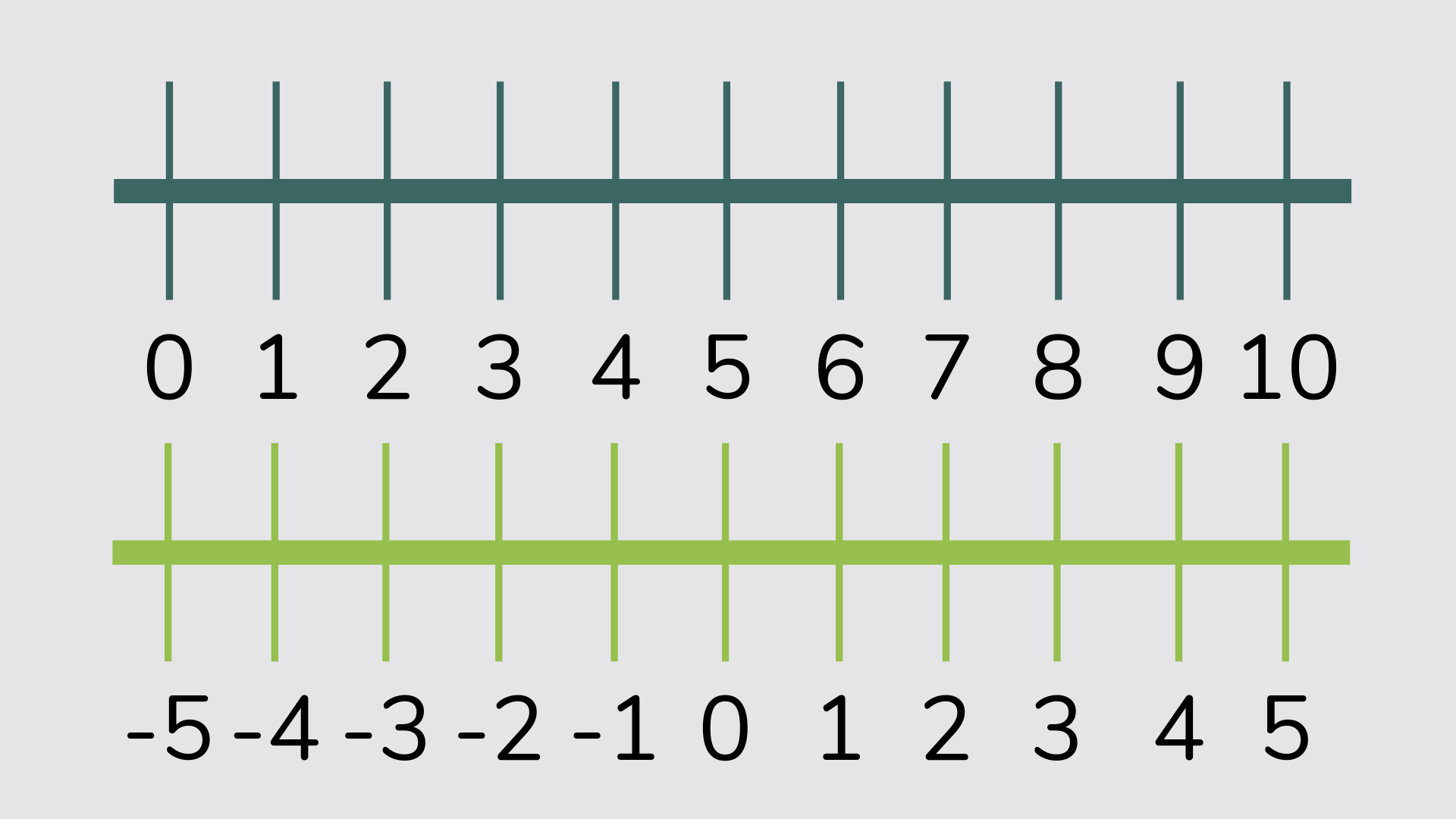
A number ladder is a number line drawn vertically.

Number sentence

A number sentence is how a calculation is written, using numbers and symbols. For example, 5 + 7 = 12 is an addition number sentence.

Read this: What is a number sentence?

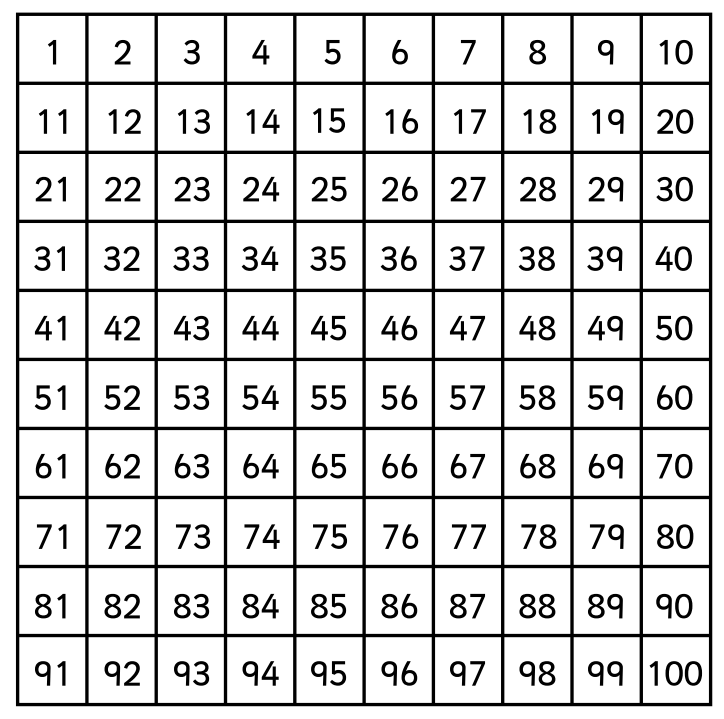
Number square

A number square is a maths aid used in primary schools, showing numbers in order from 0 up to, for example, 20 or 100. Number squares are useful for helping with counting and seeing patterns in number sequences.

Numerator

A numerator is the name for the top number in a fraction. For example, in the fraction ⅝, 5 is the numerator.

O

Obtuse angle

An obtuse angle is any angle that measures between 90° and 180°.

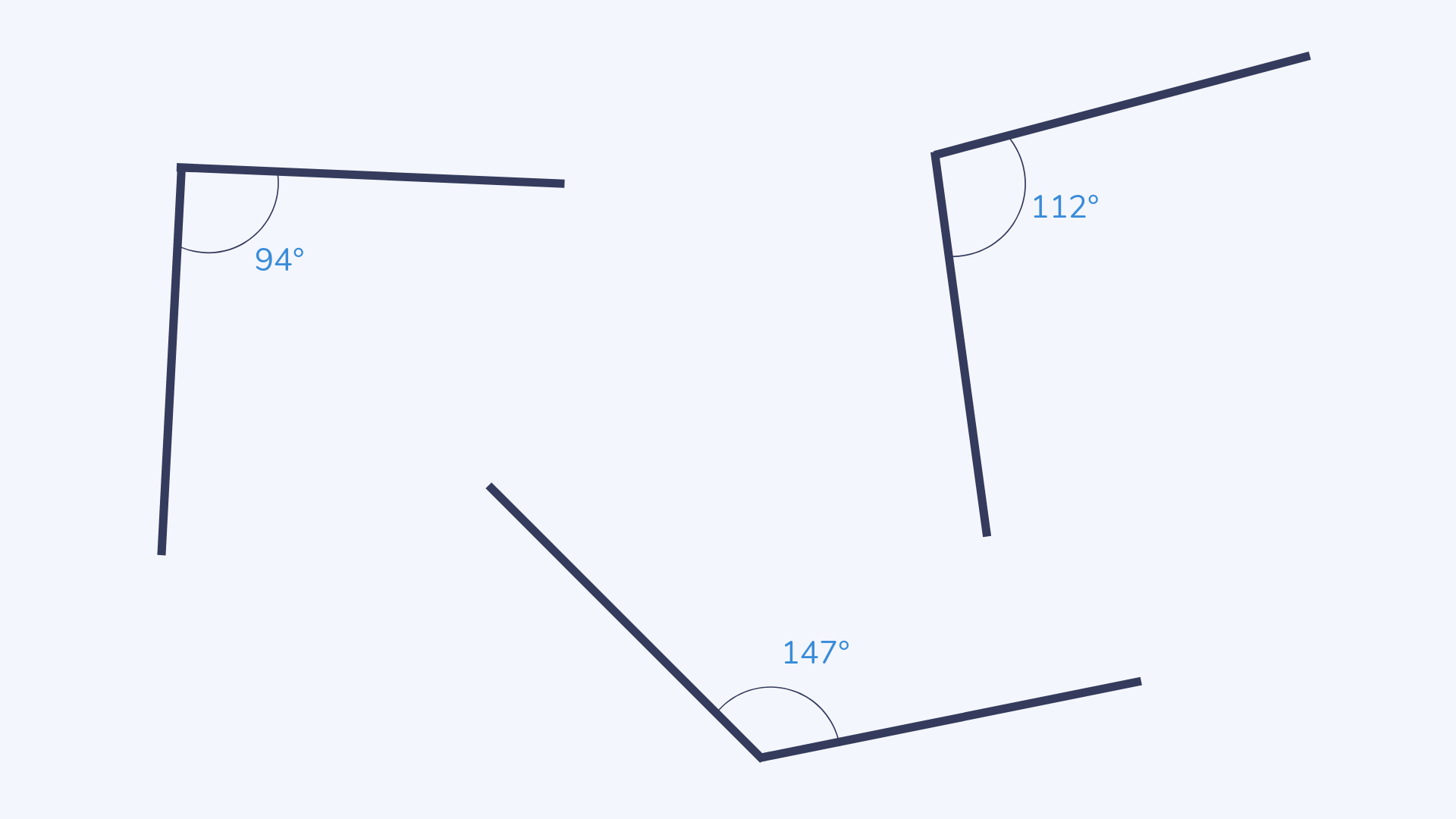
Odd and even numbers

An even number is any number that can be divided into two equal groups and always end in 0, 2, 4, 6 and 8.

An odd number is any number that can’t be divided into two equal groups and always end in 1, 3, 5, 7 and 9.

Operation

In maths, the four types of operation are addition, subtraction, multiplication and division.

In year 6, pupils are taught the order of operations, which is the order in which the four mathematical operations should be completed when there is more than one in a number sentence together.

Ordinal numbers

An ordinal number tells us what position something is in a list, often taught using dates or the results of races. For example, Ben finished in 1st place, Chris in 2nd and Alex in 3rd. The contrast of this is a cardinal number.

P

Parallel

A parallel line is a straight line that always stays the same distance from another line and never meets. Shapes are often used to teach parallel lines. For example, a square has two pairs of parallel lines.

Partitioning

To partition a number means to separate a number into separate parts (ones, tens, hundreds, thousands etc). Partitioning makes understanding place value easier and is also used when using column methods or grid methods.

For example, 5246 can be partitioned into 5 thousands, 2 hundreds, 4 tens and 6 ones or 5000 + 200 + 40 + 6.

Read more: What is partitioning?

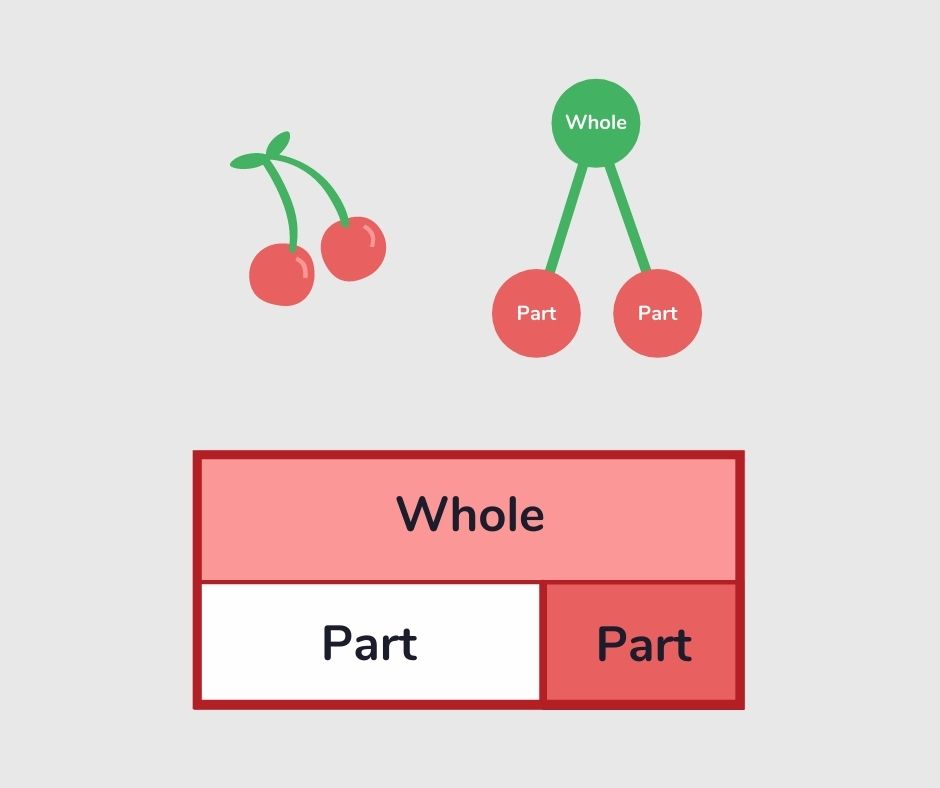
Part whole model

A part whole model is a way of representing a number and its composite parts. It is a good way to show the relationship between numbers, and the method uses partitioning. The two main ways part whole model is used are in bar modelling and cherry diagrams.

Read more: What is part whole model?

Percentage

Percentage means ‘out of 100’ and is used to show a number or ratio expressed as a fraction of 100. Children often use percentages when talking about sales in shops. For example, this £80 jacket had 20% off in the Christmas sale.

Perimeter

The perimeter is the distance around a 2D shape and is often taught using the example of fences around a field or garden.

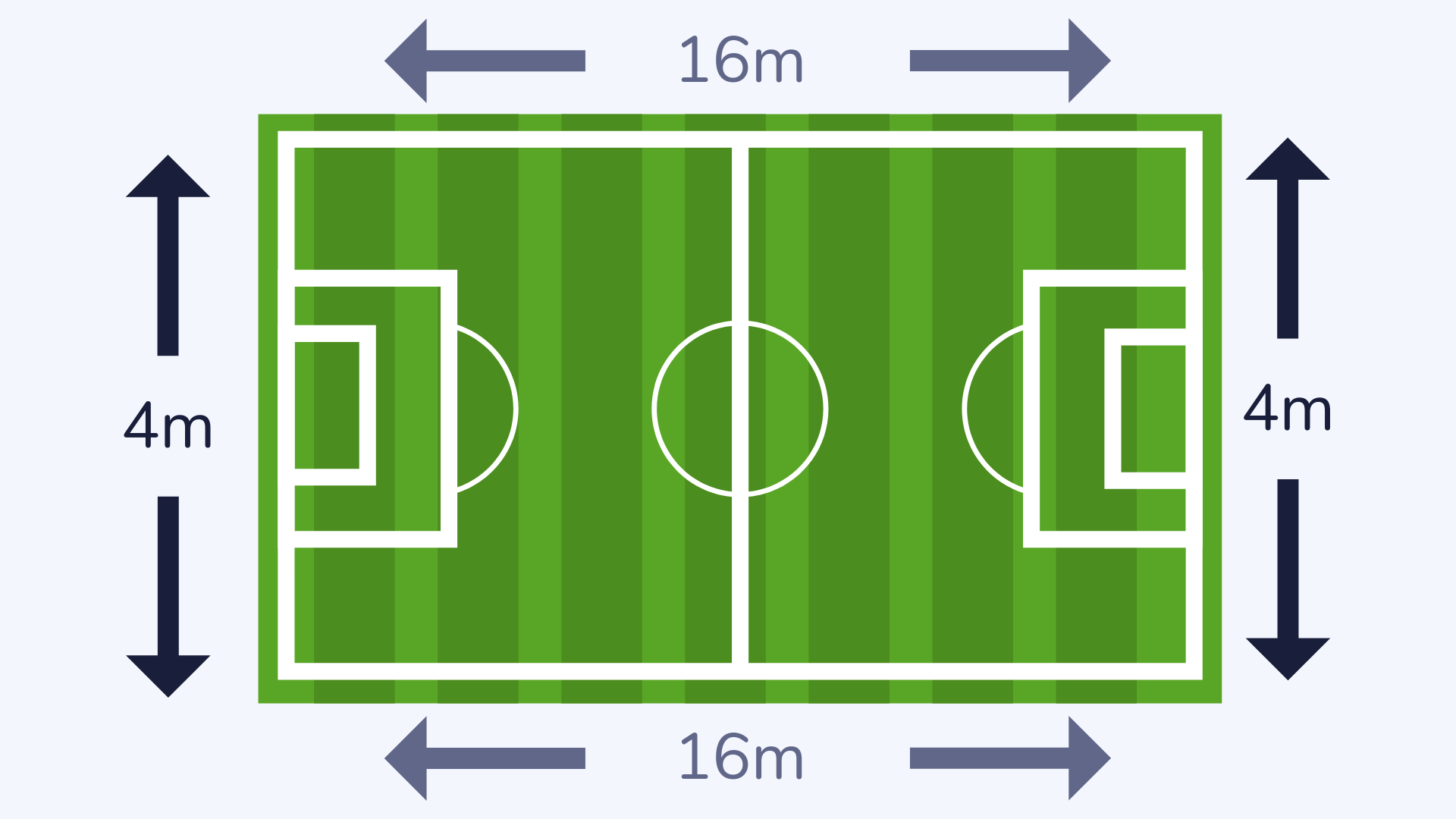
Read more: What is the perimeter?

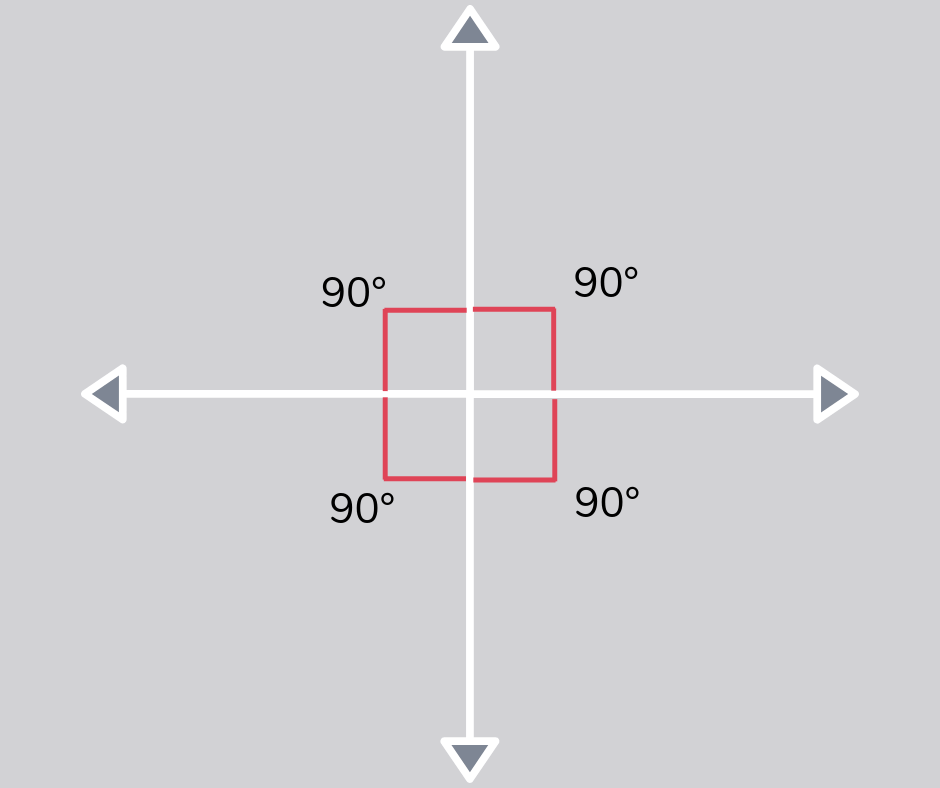
Perpendicular

Perpendicular lines are two lines that meet to create a right angle, often seen in shapes.

Pictogram

A pictogram is a type of graph that uses pictures to represent information. These are often taught in Key Stage 1 before moving onto block charts and bar charts.

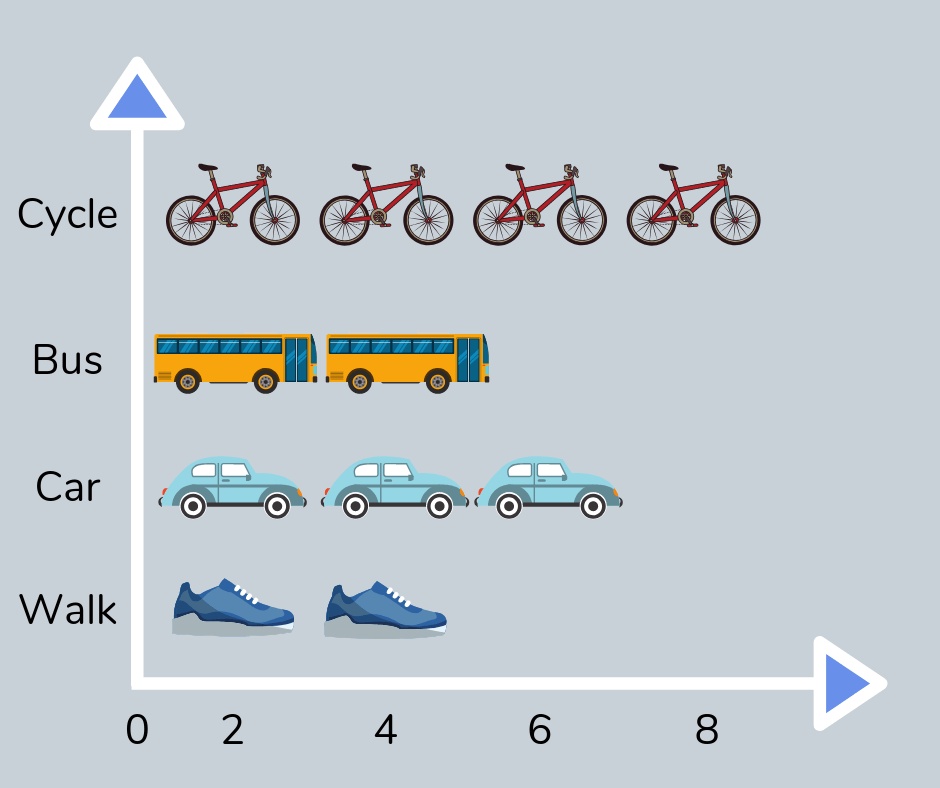
Pie chart

A pie chart is a circular chart divided into sections, representing different values, which can be fractions, decimals, percentages or angles.

Place value

The place value of a number is how much each digit in the number represents.

For example, the place value of 157 is 1 hundred, 5 tens and 7 ones.

Read more: What is place value?
Try this: Place value grid to make at home

Polygon

A polygon is any 2D shape with straight, closed sides. Any shapes with open or curved sides are not polygons. For example, triangles, squares and parallelograms are polygons, but circles and ovals are not.

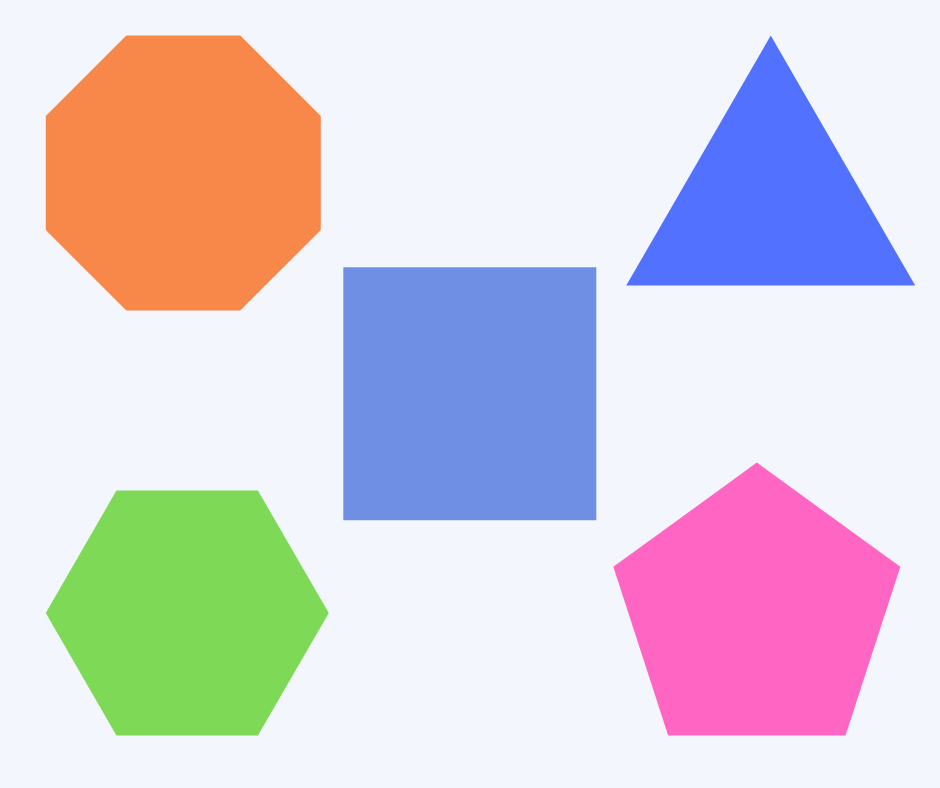
Prime number

A prime number is any number greater than 1 that can only be divided equally by itself and 1. For example, 5, 7, 11 and 13 are prime numbers.

Read more:

• What is a prime number?
• What are composite numbers?

Prism

A prism is a 3D shape with two identical flat sides and ends. Cubes and cuboids are examples of prisms.

Probability, chance and likelihood

Probability is the study of how likely or how big a chance there is that something will happen. It can be described in words, fractions, percentages or ratios. For example, there is a 20% chance of rain tomorrow.

Product

A product of two numbers is the name for the answer to a multiplication calculation.

For example, 35 is the product of 5 x 7.

Proportion

A proportion is a portion or part of a whole, and is often taught alongside ratio.

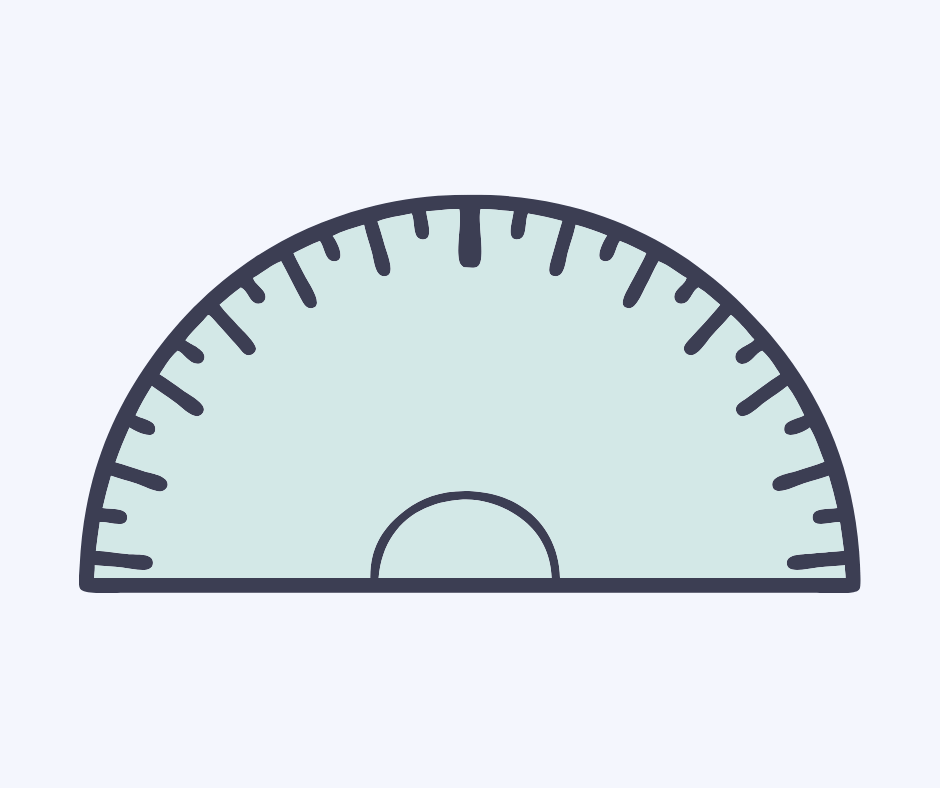
Protractor

A protractor is an instrument used to measure angles.

Pyramid

A pyramid is a 3D shape with triangular sides that join at a point, with a polygon base.

Q

Quadrilateral

A quadrilateral is any 2D shape with four sides, including a square, rhombus, kite and trapezium.

R

Radius

The radius is the distance from the centre of a circle to its circumference and is half the diameter.

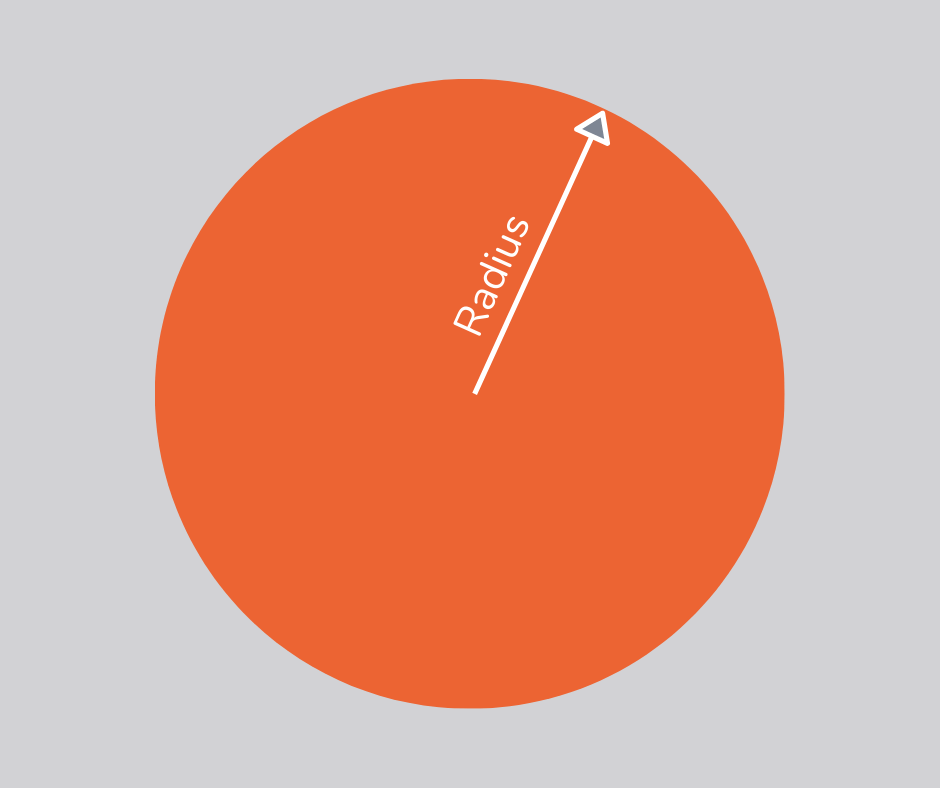
Range

The range of a set of numbers is the difference between the smallest and largest numbers in the set.

For example, in the set of numbers 50 to 60, the range is 10.

Ratio

A ratio is used to compare values, showing the relative value of one to another. It is taught using real-life examples, such as comparing the number of boys to girls in class. For example, the ratio of boys to girls was 2:1, meaning there are two boys for every one girl.

Reflection of shapes

A reflection of a shape is a drawing of a shape reflected in a mirror line, with the reflection on the other side of the line but facing in the opposite direction.

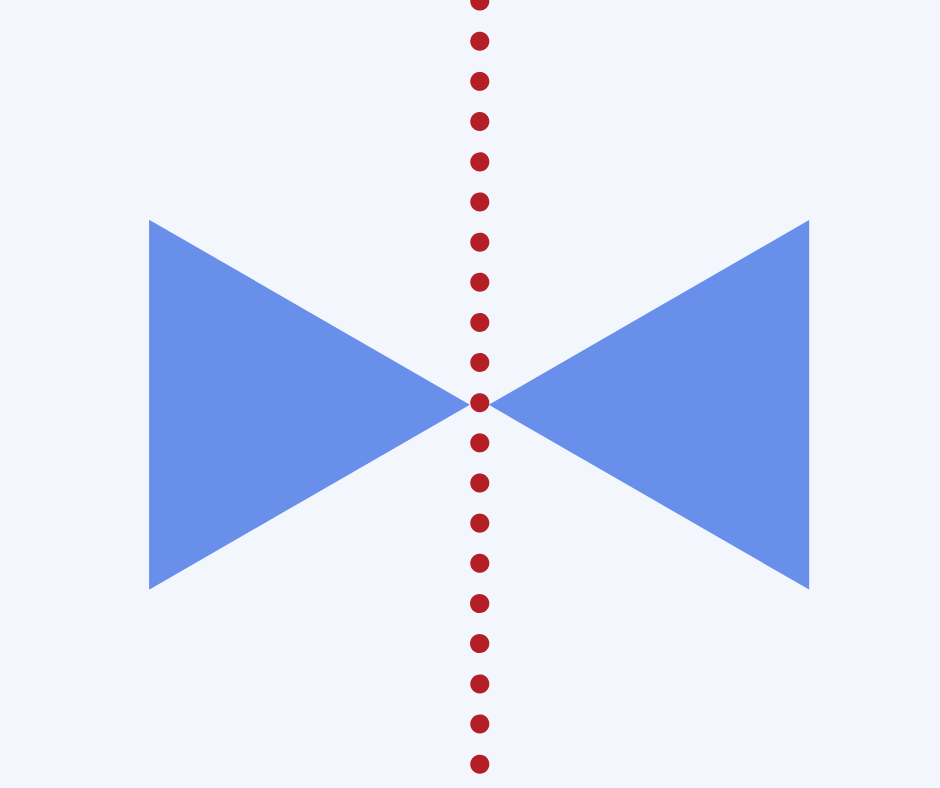
Reflective symmetry

Reflective symmetry is a type of transformation, looking at when a shape or pattern is reflected in a mirror or line of symmetry. The reflected shape should be exactly the same size and distance from the mirror line as the original.

Reflex angle

A reflex angle is any angle between 180° and 360°.

Regular and irregular shapes

A regular shape is one where all the sides and interior angles are equal, whereas an irregular shape has sides and angles of different lengths and sizes.

Read more: What are regular and irregular shapes?

Rekenrek

A rekenrek is a counting frame, similar to an abacus. It has ten beads on each row, five white and five red which supports the development of number sense.

Read more about rekenreks here.

Right angle

A right angle is an angle that measures 90°. It is also known as a quarter turn, as it is ¼ of a full turn, which measures 360°.

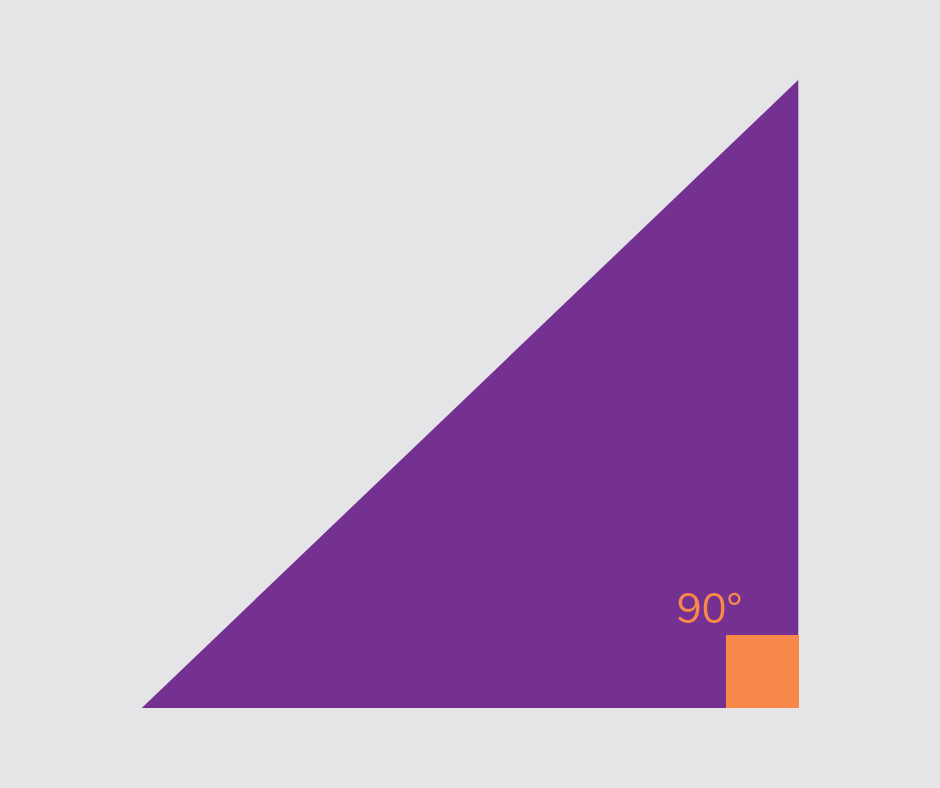
Right-angled triangle

A right-angled triangle is a 2D shape with three sides and one angle that measures 90°.

Roman numerals

Roman numerals are the numbers used in ancient Rome, with letters from the Latin alphabet representing certain numbers. They are commonly taught using years. For example, V = 5, X = 10, C = 100, M = 1000, so 1066 is MLXVI.

Rotation of shapes

A rotation of a shape is when a shape is moved around a fixed point, either clockwise or anticlockwise and by a certain number of degrees. However, the shape doesn’t change size.

Rotational symmetry

Rotational symmetry is a type of transformation, where a shape is turned around a central point, without changing its size.

Rounding numbers

To round a number means to adjust it up or down to a number that makes calculating with it easier. Numbers are usually rounded up to the nearest 10, 100 or 1000, with decimals being rounded to the nearest whole number, tenth or hundredth. There is a rule that if a digit is 4 or less it rounds down and if it is 5 or more it rounds up.

For example, 426 rounds to 430 to the nearest 10, but 400 to the nearest 100.

Repeated addition

Repeated addition is a technique used to teach multiplication in Key Stage 1, where children add ‘lots’ of numbers together.

For example, 3 ‘lots’ of 5 is 5 + 5 + 5 as well as 3 x 5.

S

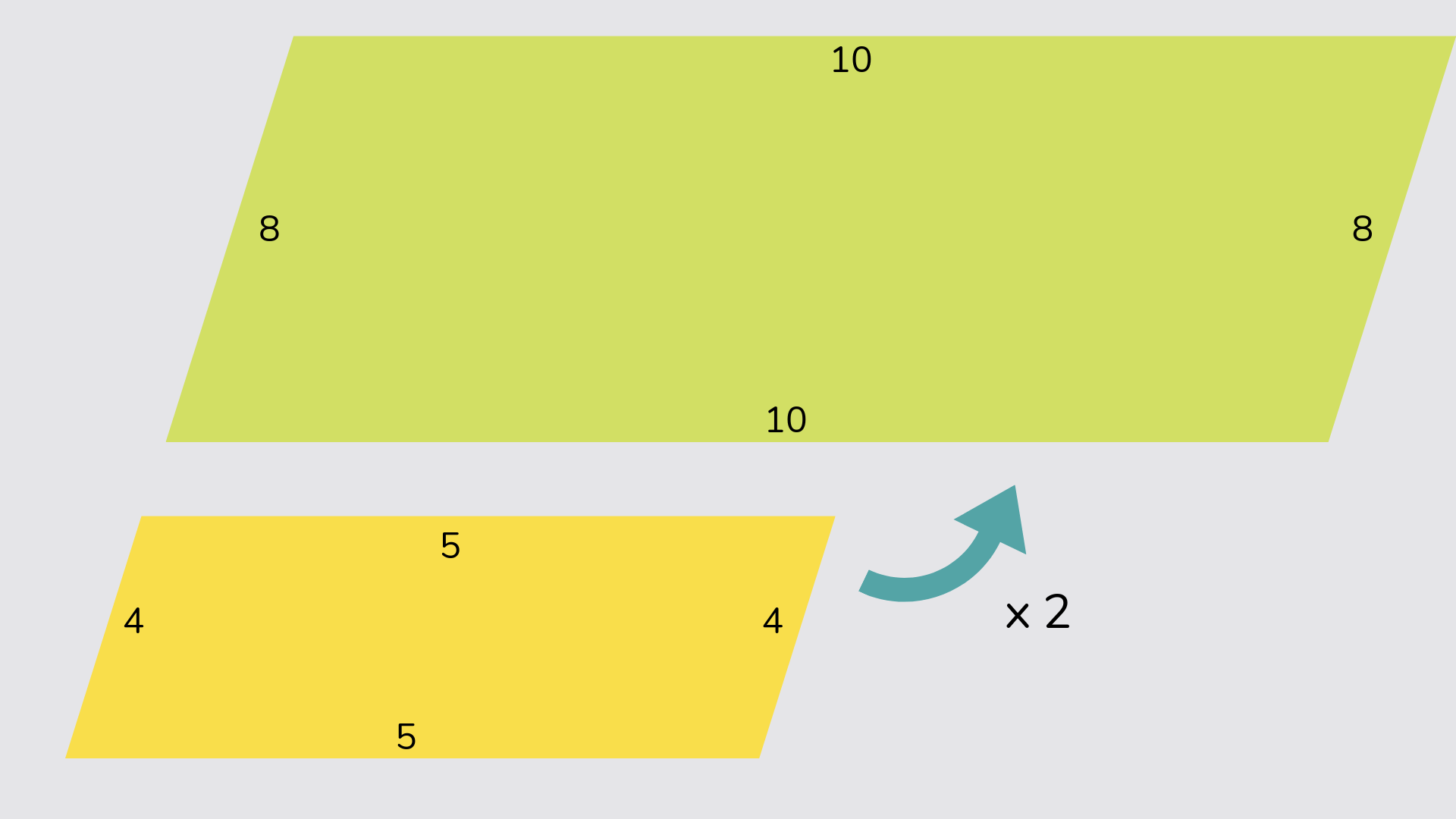
Scale factor

A scale factor is used when we increase or decrease a 2D shape in size, so we make the shape larger or smaller depending on the scale factor. For example, this shape has been increased by a scale factor of 2.

Scalene triangle

A scalene triangle is a 2D three-sided shape where all the sides and angles are unequal.

Shared between

‘Shared between’ is a phrase used when introducing division, to show how a set of objects can be ‘shared’ into equal sized groups.

Simplifying fractions

To simplify a fraction means to reduce it to its lowest form, by dividing the numerator and denominator by the same number. For example 8/10 can be simplified to ⅘ by dividing both the numerator and denominator by 2.

Square numbers and Square roots

A square number is the result of multiplying a number by itself. When writing this, we write a small two next to and above the number. For example, 7² = 7 x 7 = 49.

Read more: What is a square number?

Standard and non-standard units

Standard units are the units of measurement we normally use to indicate the length, mass or capacity of an object. For example, centimetres, metres, grams, kilograms, millilitres and litres.

Non-standard units are used by when introducing measurement in KS1, for example the length of a pencil or hand spans.

Sum

A sum of two numbers is another name for the result of an addition calculation. For example, the sum of 15 and 23 is 38.

Symmetry

When a picture or shape is the same on both sides, we call it ‘symmetrical’, and this can be shown by drawing a line of symmetry through the centre and seeing if both sides are the same.

Read this: What is a line of symmetry?

T

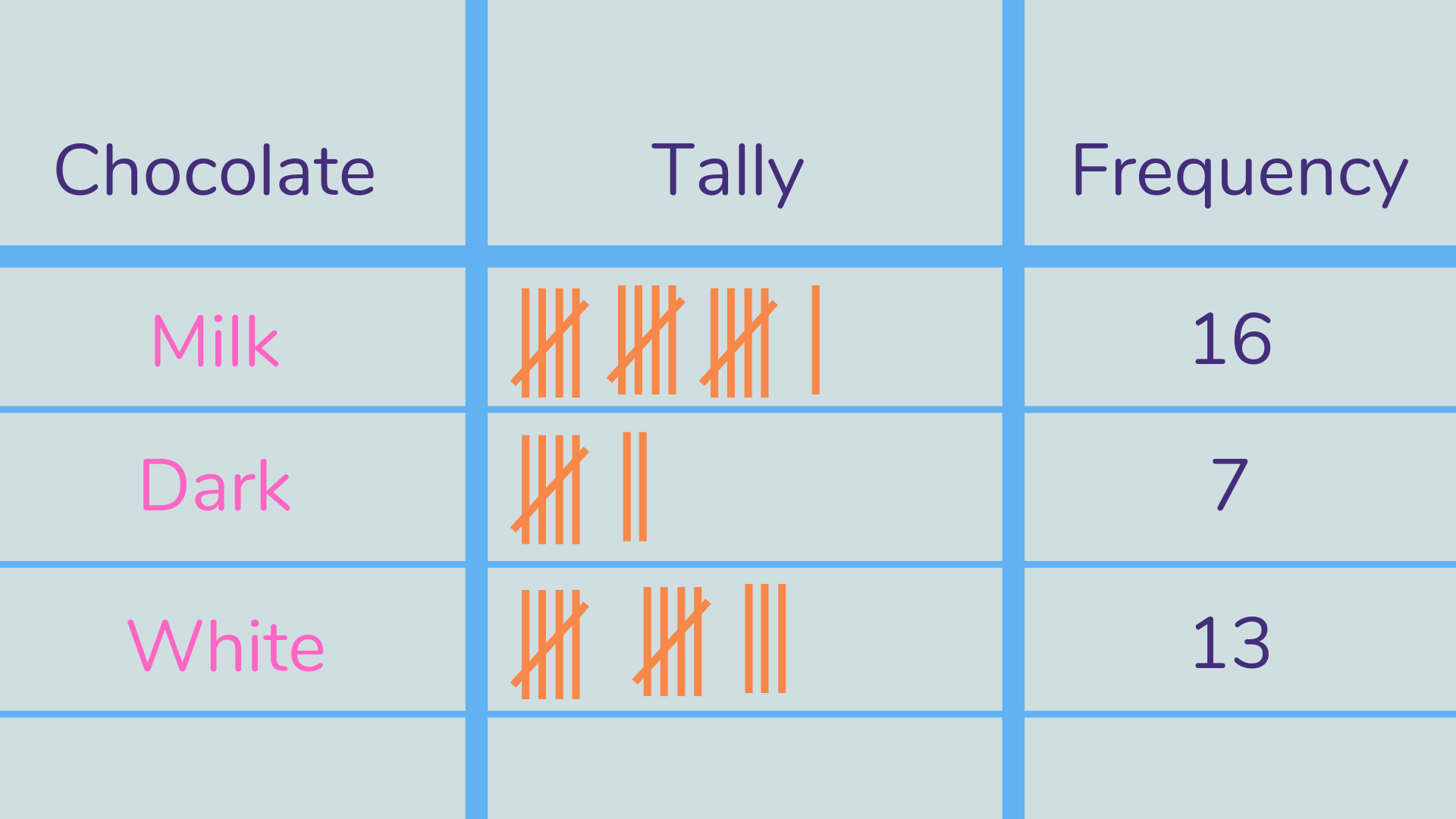
Tally chart

A tally chart uses marks instead of numbers to represent information. One vertical mark is used to represent each one unit, with five being shown as a fifth line crossed through the first four lines.

Tessellation

When shapes fit together exactly with no gaps, we call this Tessellation. An example of this in real life are floor tiles.

Time intervals

A time interval is the length of time between two times. For example, the time interval between 1:15 and 1:45 is 30 minutes.

Translation of shapes

Translation is a type of transformation, where a shape is moved into a new position, without being changed in any way.

Triangle

A triangle is a 2D shape with three sides, angles and corners.

Triangular number

A triangular number is a number that can make a triangular dot pattern.For example, 1 + 2 = 3, 2 + 3 = 5, 3 + 5 = 8, 5 + 8 = 13 etc.

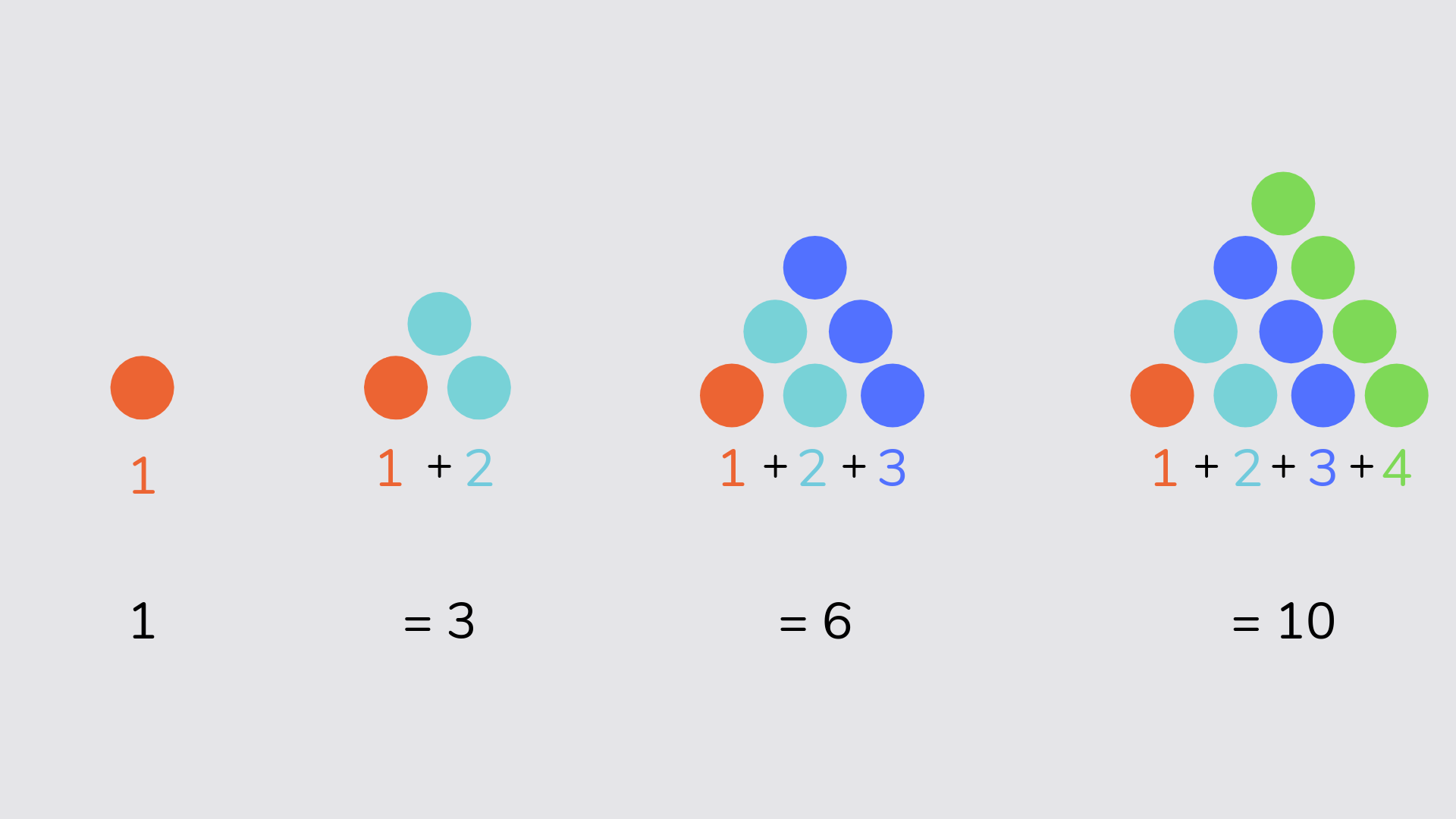
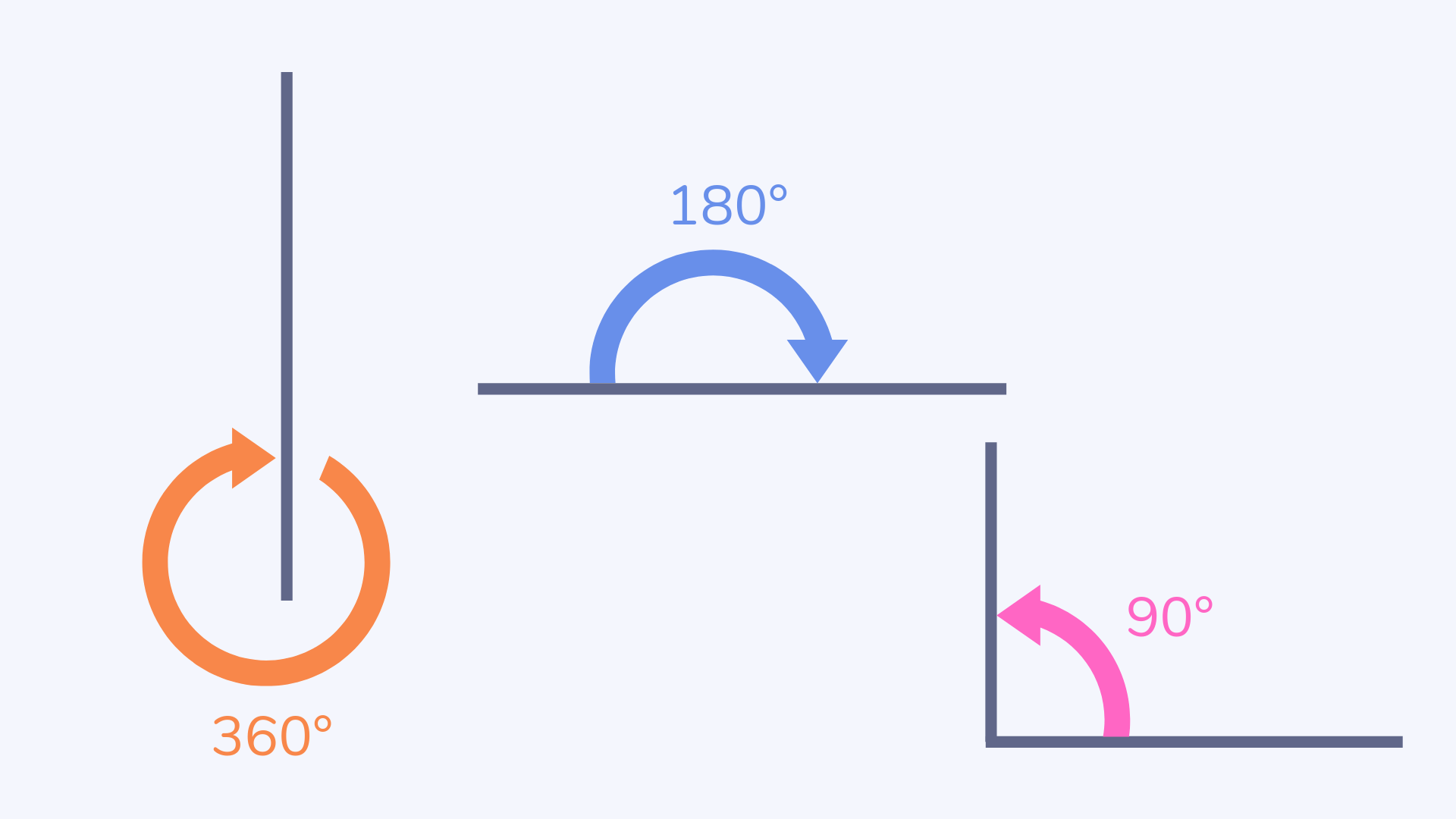
Turns

Turns are a movement in a circle, with a quarter turn being the same as 90°, a half turn as 180° and a full turn as 360°, either clockwise or anticlockwise.

Two-step and multi-step problems

A two-step problem is a word problem which needs two calculations to solve it. A multi-step problem requires more than two calculations to solve it.

Read more: Two step word problems and multi step word problems?

U

Unit and non-unit fractions

A unit fraction is any fraction with 1 as the numerator, whereas a non-unit fraction is any fraction with a number greater than 1 as the numerator. For example, ⅙ is a unit fraction, whereas 2/6 is a non-unit fraction.

Read this: What is a unit fraction?

Read more: What is a non-unit fraction?

V

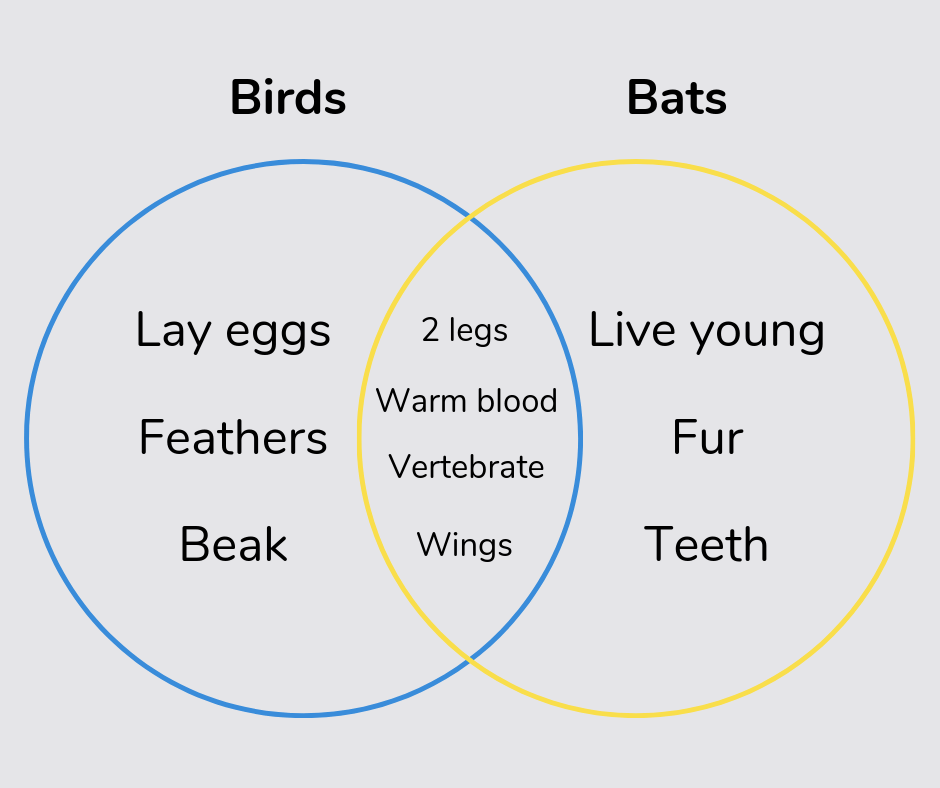
Venn diagram

A Venn diagram is a visual way of sorting different objects or numbers into overlapping circles with different rules, with anything in the overlapping part sharing both rules.

Read this: What is a venn diagram?

Variation

In primary maths, there are two types of variation, conceptual and procedural variation.

Conceptual variation means looking at a maths idea in various representations. For example, showing a number using multilink, diennes block, hundred square or partitioned, to explain place value.

Procedural variation is used to support a child’s deeper understanding of a maths process by extending a problem by varying the number, varying the processes to solve a problem or varying the problems by applying the same method to a group of similar problems.

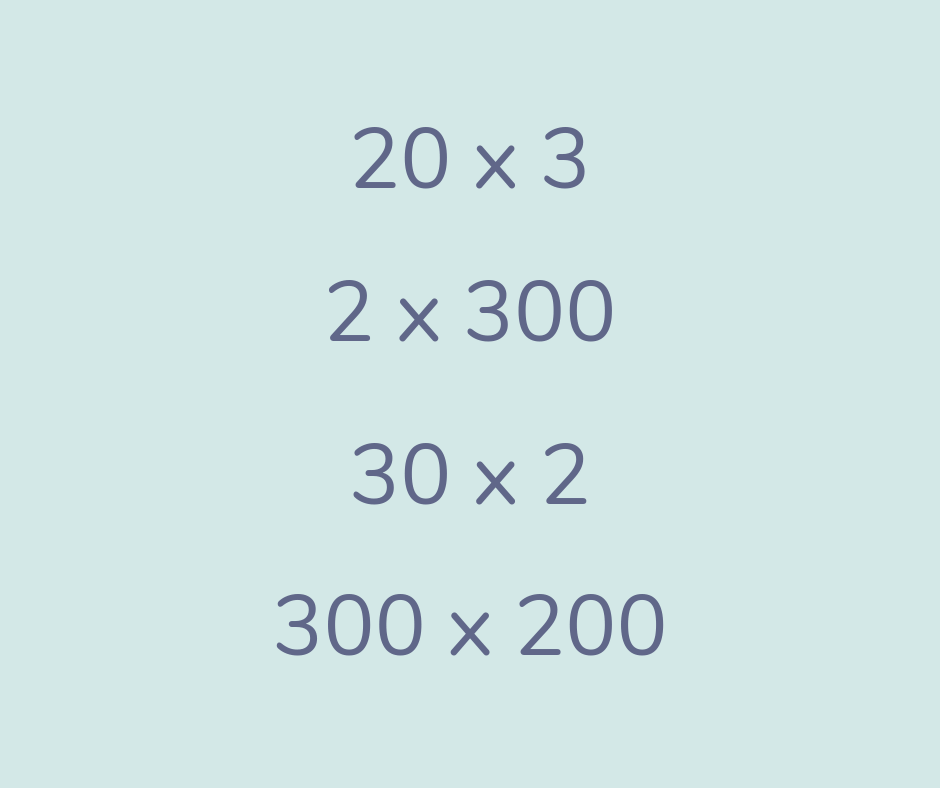
Vertex/vertices

Vertex is another name for a corner of a 2D shape or the points where edges in a 3D shape meet.

Vertical

A vertical line runs up and down, from top to bottom.

Volume

The volume is the amount of space an object occupies, especially 3D shapes. Children will learn the formula for finding the volume of a shape, which is the length x width x height, with the answer having units with a cube number, for example cm³.

W

Word problem or story problem

A word problem or a story problem is a real-life situation where a maths calculation is needed to solve a problem. For example, ‘If half a class of children have pets and there are 36 children in the class, how many have pets?’

Read this: Word Problems Explained

X

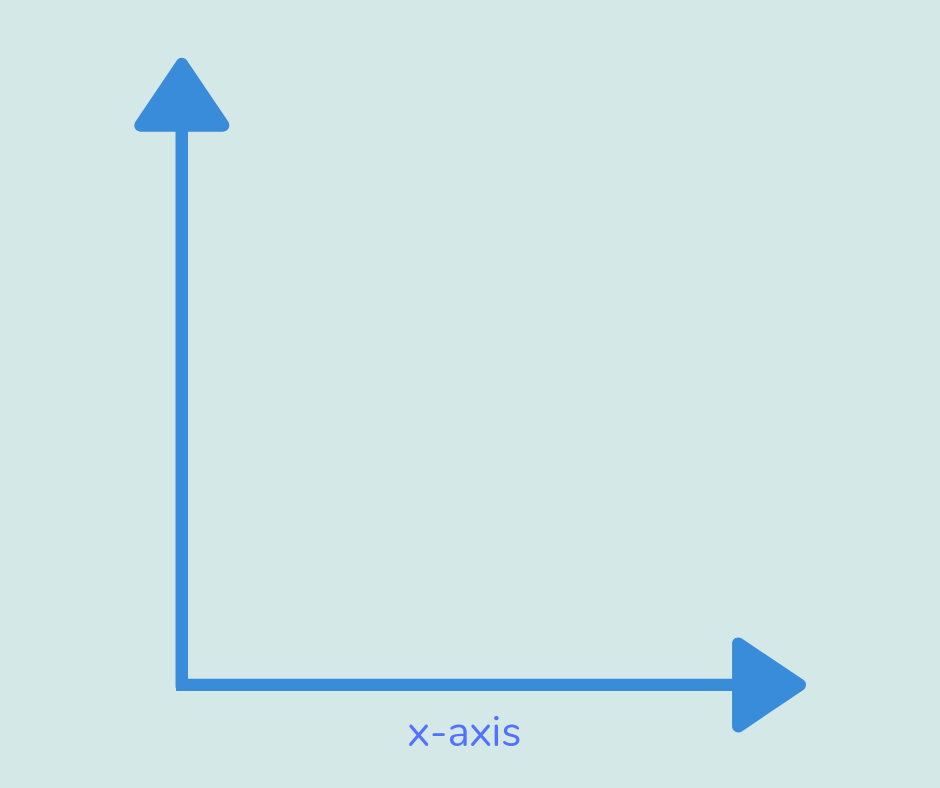
X-axis

The x-axis is the horizontal axis on a graph, along which we find the x-coordinate (by going ‘along the corridor’).

Y

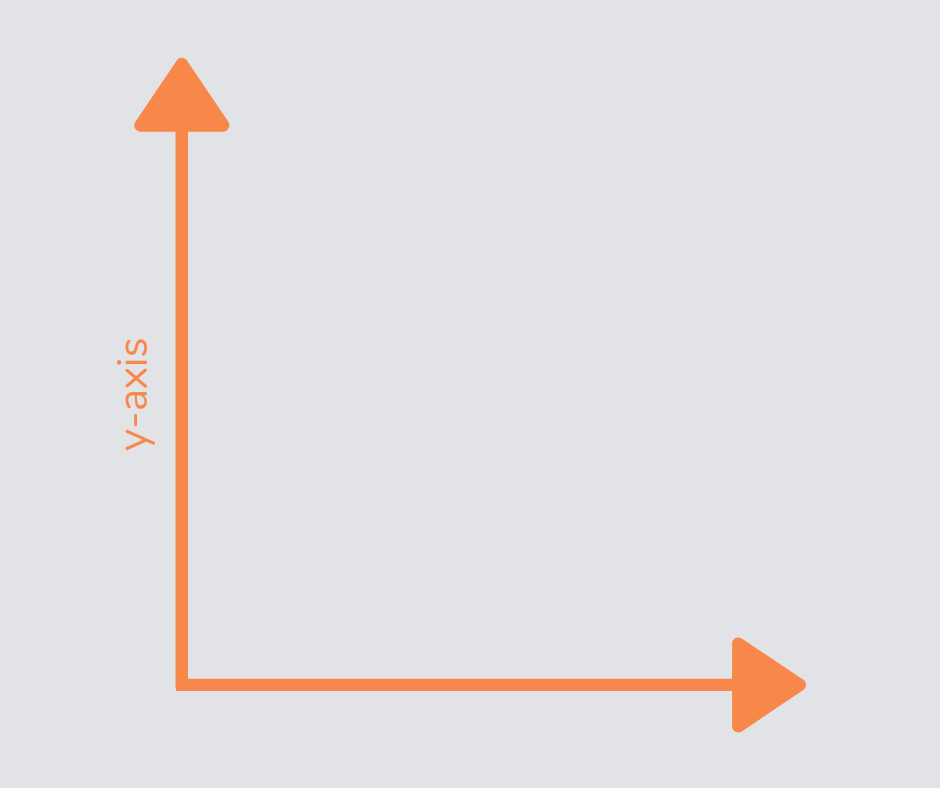
Y-axis

The y-axis is the vertical axis on a graph, along which we find the y-coordinate (by going ‘up the stairs’).

Z

Zero

Zero is a placeholder between +1 and -1, it has no value but changes the value of other numbers. For example, in the number 703 it changes the number 73 to the much larger 703.

---

In our primary maths dictionary for parents we’ve tried to include as much of the maths terminology your child will be learning at KS2 as possible, but we know that we may have missed something!

If that is the case then let us know which numeracy based terms we have missed, and we’ll be more than happy to add them to this A to Z maths dictionary!