What Is Mean In Maths And How Can You Calculate An Average? Explained For Primary School

Find out what the definition of mean and average are, when they are taught in school, and how you can help children to understand mean and average as part of their maths learning at home.

What is mean?

Mean is a type of average used to calculate an average of a given data set.

To find the mean average value or arithmetic mean of your data, you must first add up all the numbers. Then you need to divide this sum of the values by the number of data points (or total number of numbers).

There are also other types of mean, such as ‘sample mean’, ‘geometric mean’, and ‘harmonic mean’ that use the sum of the numbers of a dataset to calculate the average value.

However, using the mean is not the only way to find the average of a data set. There are other types of averages or measures of central tendency, including:

• The median – which is also known as the middle number or middle value
• The mode – or modal number is the data value which occurs the most
• The range – which is the difference between the smallest value and highest value

Mean maths examples

Visualising mean

Mean is often taught and explained through abstract methods as soon as students in Year 6 are capable of manipulating the required numbers needed to find the mean or average amount. However, it is important that students understand what is happening when they are finding the mean of a data set.

The pictures below show just that.

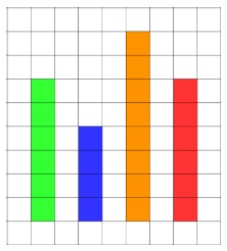
If this represented a data set of points scored by four teams in a game, we could find the mean by adding up all the data points and dividing the sum by the number of data points in total. While this reaches the answer of a single number, it does not provide a conceptual understanding of what is happening to that data.

Before getting students to carry out an algorithm, it would be better to demonstrate to them what is happening when they carry out this process.

By finding the mean, we want to find the average points scored in a game across all teams. The way to do this would be to see if we can get all data points to the same height by manipulating the data (when doing this with a class, I would get them to make these representations physically with cubes or counters).

Read more: Concrete Pictorial Abstract

We can see that by removing two orange cubes and placing them on top of the blue cubes, then all data points would have the same value.

This is demonstrated in the next picture.

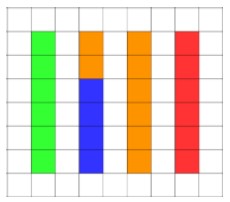
With all data the same height, we can see that the mean average is the size of each part when a quantity is shared equally.

How do you calculate mean?

To find the mean, you first need a set of values. This can be obtained by any means, but it is more meaningful when it can be related to your class. Here’s a frequency table containing discrete data (rather than grouped data) with no outliers.

Name	Number of books read
Fred	5
Harry	4
George	1
Dudley	2
Ron	5
Arthur	3
Ginny	8
Albus	4

As mentioned earlier, to find the mean average value, you must first add up all the given set of data points and divide the sum by the total number of values. This means that students will need to first find the total number of books read by the class.

As they are in Year 6, I would encourage them to use their mental arithmetic skills to find the total by looking to make number bonds that they are comfortable with. Going in ascending order, 5, 4 and 1 make a number bond to 10.

2, 5 and 3 make a number bond to 10.

8 and 4 make 12, so this gives a total of 32.

The next step would be to divide 32 by the number of values that are in the (bimodal) data set. As there are 8 students, 32 would have to be divided by 8. Students should be able to use their multiplication facts (8 × 4 = 32) to know that 32 divided by 8 would give 4. This would make the mean value of the set of numbers above 4.

When do children learn about mean and average in school?

Whilst studying statistics, students in Year 6 will be expected to learn how ‘to calculate and interpret the mean as an average’. Year 6 students have always had to work out the mean as an average, but before the amended national curriculum in 2014 came into effect, students also had to work out the median mode and range. The 2014 curriculum amendments only made it mandatory to teach mean.

Read more: Teaching Statistics And Data Handling KS2

How do mean and average relate to other areas of maths?

Finding the mean can improve the fluency of addition skills when having to add up a number of data sets, and can encourage students to use mental maths methods to do these additions. Students can also find more complex averages from fractions and decimals as well as data sets with both positive numbers and negative numbers. Likewise, it can help students practice seeing division as the inverse of multiplication.

Read more: What Is Fluency In Maths & How Do Schools Develop It?

How do mean and average link to real life?

Finding the mean is just one of the ways that people find averages out of a set of data. The Office for National Statistics uses mean to find the average age of the population. Any role that involves looking at data will likely use the mean to help draw conclusions from the data.

Mean maths worked examples

Let’s go through some step-by-step worked examples for calculating the mean in maths.

1. Find the mean.

Name	Number of detentions in a year
Fred	18
Harry	35
George	21
Ron	26

To find the mean, first, add all the data sets.

To solve this, we need to add the list of numbers, 18, 35, 21 and 26. This is 100.

Next, we divide by the number of data sets. As this data is for 4 people, the number of data sets is 4. This means we need to divide 100 by 4. This is 25.

2. Find the mean.

Name	Number of merits
Fred	45
Harry	37
George	43
Ron	46
Ginny	54

To find the mean, first, add all the data sets.

To solve this, we need to add 45, 37, 43, 46 and 54. This is 225.

Next, we divide by the number of data sets. As this data is for 5 people, the number of data sets is 5. This means we need to divide 225 by 5. We can do this by partitioning 225 into 200 and 25. 25 divided by 5 is 5 and 200 divided by 5 is 40. When these are added together, you get 45.

The mean number of merits is 45.

Mean maths practice questions

1. Use a concrete manipulative to share these quantities out equally.

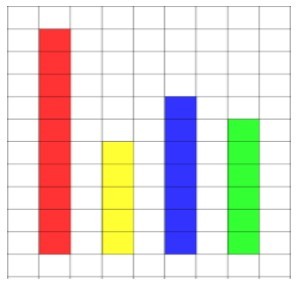
Answer: Each row should have 7 blocks.

2. Complete this sentence stem:

To find the mean, first ______ all the data sets and then ______ by the ______ of data sets.

Answer: To find the mean, first add all the data sets and then divide by the number of data sets.

3. Find the mean.

Name	Number of books read
Fred	7
Harry	4
George	2
Dudley	4
Ron	3

Answer: The mean is 4.

4. Joshua has tried to find the mean. Can you spot his mistake?

Pig 1	Pig 2	Pig 3
54kg	55kg	59kg

54 + 55 + 59 = 168kg

168 ÷ 6 = 28

The mean weight is 28kg.

Answer: Joshua’s mistake is that he divided by 6 and not 3.

5. Find the mean.

Name	Number of cookies eaten
Trevor	25
Pritesh	32
Janice	28
Moe	35
Sue	30

Answer: 126

Wondering how to explain other key maths vocabulary to your children? Check out our Primary Maths Dictionary and take a look at What Are Mean Median Mode Range?