Mental maths at KS1 and KS2 and how you can develop the skills children need

Mental maths is a crucial skill that children develop throughout KS1, KS2 and beyond. Here are some suggestions on how you can teach it most effectively. 

What is mental maths

Mental maths is the ability to work out calculations in your head (not just addition sums). It means being able to give an answer to a question without having to write down every step of the calculation, although making the odd note is acceptable. Good mental maths skills in primary school generally show that a child has grasped what numbers represent, can spot patterns, and has developed excellent fluency and recall.

Fluency and mental maths 

We most commonly associate mental maths with mental calculation, but this may also bring connotations of rote learning and parroting known facts with little conceptual understanding. However, our fluency in mental maths relies on a firm and thorough understanding of number concepts and a flexibility with numbers which goes well beyond memorisation.

Memorisation may play a part in elements such as times table recall and number bonds, but these must be laid on top of firm foundations in the number system. An understanding of place value, partitioning, doubling and halving, form the basis of mathematical fluency and accuracy. 

Mental maths at primary school follows a clear progression

Mental maths requirements for each year group through Key Stages 1 and 2, build on each other. From number bonds to 20, through to cubed numbers, with incremental steps along the way. 

Maths concepts are introduced gradually and may start with physical representations using manipulatives (also known as concrete examples). Then children move to pictorial/visual representations of numbers and operations (such as bar modelling and number lines). Once this understanding is grasped we move to the symbols used for numbers and operations (the abstract) and it is the abstract element which we apply most commonly to mental maths calculations. However, this abstract understanding of number is built over time and may be revisited starting with the physical use of manipulatives as each new concept is introduced. 

In a lesson you may go through all phases – from physical representation through to practise of the symbols in formal written calculations – and gradually move to the manipulatives being available to students who need it.

In a lesson on addition, for example, you may ask some children to count beads out in front of the class, then show the counting while using a counting stick, and then move to children counting out beads themselves, drawing those onto their sheets of paper, and then adding the numbers and addition sign. 

Some children will not need to use the physical beads for their written part of the lesson, where other children may choose to keep that step while they practise. 

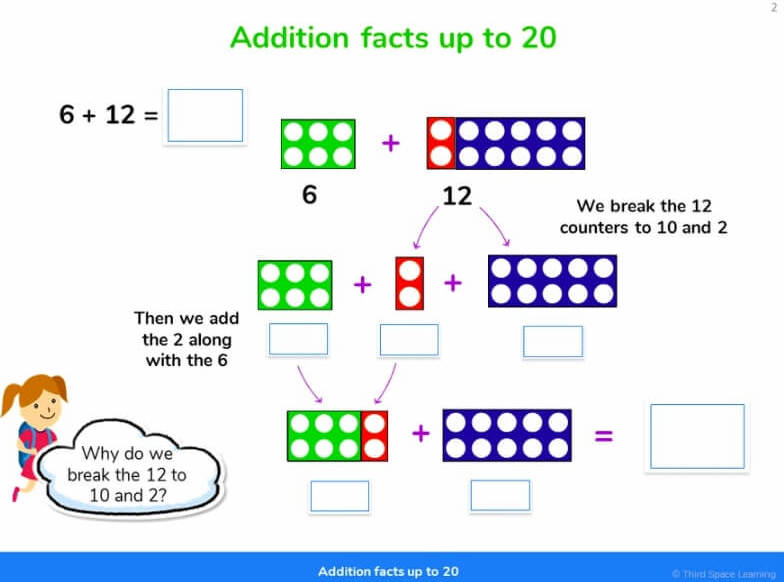
Why we need to teach mental maths and number facts

Children are unlikely to work out for themselves, the short cuts and mental devices that we have for making mental calculations less taxing. Therefore, we need to actively teach these mental maths strategies, together with the series of number facts, that will be needed for rapid recall each year in primary school. 

Each child may find they are recalling the number facts mentally at different stages of each new concept learnt, but opportunities to assess a child’s mental maths strategies can present at any stage. 

When learning addition a child may jump straight from adding together beads on the floor, to adding those numbers mentally in their head and then recalling those facts when opportunities to apply those known facts arise.

For other children they may not be able to recall the number association until they have progressed to writing the numbers down to remember the repeated number facts. 

Read more: 

• Mental Maths Strategies
• Mental Maths Questions 
• Number Facts 

Mental maths in the national curriculum 

Mental arithmetic is a key element of the Year 6 SATs, particularly for the SATs Arithmetic Paper 1. 

However, it is also expected in the Year 2 SATs, as without some good recall of known number facts most children will run out of time to complete the tests. 

The national curriculum for Years 1 and 2 states that “the principal focus of mathematics teaching in key stage 1 is to ensure that pupils develop confidence and mental fluency with whole numbers, counting and place value. This should involve working with numerals, words and the four operations, including with practical resources (for example, concrete objects and measuring tools)”.

What you should know about teaching mental maths topic by topic 

Mental maths skills within place value

Place value is a vital element of mathematical understanding without which pupils struggle to build fluency and accuracy. It can take a lot of time and repetition in Years 1 and 2, to ensure the firm foundations needed for maths in Key Stage 2. Place value is how we learn to partition numbers, understand the true value of each digit in a number, and how we can solve many larger number problems mentally. Knowing, for example, that 24 + 17 = 20 + 10 + 4 + 7, can help us to work out that problem quickly in our heads without needing to use a formal written columnar method. 

When using written columnar methods, our understanding of place value, alongside good mental maths skills, help us to calculate each column accurately and ensure our answer is correct. Our mental math skills can also help us to check if the answer is likely to be right. For example if I worked out 19 x 21 and had an answer around 400, I could estimate that is likely to be correct as I can round each number to 20 and I know 2 x 2 = 4. 

Known number facts – a combination of number bonds and learnt multiplication tables – help us to mentally calculate large numbers. An understanding of place value is vital in helping us to be flexible with the numbers without ending up with an answer which is wildly off mark. 

In KS1 children start to grasp the concept of place value for 2 digit numbers, and should be able to recall and apply number bonds to 20. Recall in these formative years can be developed using maths games and targeted maths questions, as well as through more formal teaching methods. 

In Year 3 pupils are taught place value to 3 digits: hundreds, tens and ones. And by Year 6 children are expected to understand place value all the way up to 10 000 000. You can see from the difference in those four years that any misconceptions around place value earlier on will cause much bigger issues as those numbers increase in value. 

An understanding of multiplying and dividing by 10, using such resources as our Place Value Concertina, also helps pupils to understand the value as the number of digits increases/decreases. Base 10 and Cuisenaire rods are also popular manipulatives which help with the concrete representation of much larger numbers – adding beads together is fine for single and even small 2-digit numbers but gets rather unwieldy when dealing with 3-digit numbers and beyond!

Mental maths skills within addition and subtraction

The first building blocks of addition and subtraction will usually start in the Early Years classroom, although they may start very informally. Even before school starts, 2 and 3 year-old children also gain an understanding of addition and subtraction through ‘more’ and ‘less.’ “Please may I have more apple juice?”, “Why have I got less than my brother?” and so on!

Such questions lead to the early introduction of counting on and counting backwards; starting with one more and one less. Children will then, in class, be offered bowls of counters, or objects such as toy cars, and encouraged to count them out of the bowl. This will build their 1:1 association as well as repeated practise of counting forwards and backwards.

Alongside this, teachers often show a pictorial representation – this may be a counting stick or string of beads or could be a visual representation of these. This move from physical objects in the hand, to a pictorial representation, is working towards children doing their own visual representation by drawing counters onto paper, before they start writing numbers and using the symbolic representation. 

While children are working on this move from physical to symbolic representation of maths number facts, it is possible to also introduce some repetition of number bond facts. This often starts with repetition of numbers bonds to five, then ten, then 20. 

By the end of Year 2, in the maths SATs, pupils are expected to be able to rapidly recall number bonds to 20, so having regular opportunities to repeat them both in lessons and as separate recall practice, will build fluency. Throughout primary school it is important that known facts are regularly repeated and practised, or children will lose their fluency in those early foundation facts quite quickly as new facts are introduced. 

There is no longer a specific mental maths test in Year 6 SATs but there are questions throughout the arithmetic papers in Year 2 and Year 6, which will rely on rapid recall of number facts in order to answer all the questions in the time given. These learnt facts will also then be applied when tackling columnar written methods to speed up the process.

Mental maths skills within multiplication and division

At the end of Year 4 children will take an online statutory times tables test to check their rapid recall of multiplication tables from 1-12. The foundations for this start in Year 1 and 2 where they will begin by doubling numbers. By the end of Year 2, students should know the 1, 2, 5 and 10 times tables. This includes not just the recall of them by rote but also the application of the facts. They will also be doing halving of numbers and begin their understanding that double is the opposite of halving a number or cake.

These skills can be practised through practical tasks such as baking as children can apply their double knowledge to simple elements such as how many eggs you need. It is important that this starts with single digit numbers as a sudden jump to trying to calculate double 220g of flour might be a leap! But they will be used to counting on in 10s so this could be practise for counting on, in increments of 10g of flour at a time, using a measuring spoon, for example. 

The inverse relationship between multiplication and division is not usually explicitly taught until Year 3 but through doubling and halving children will have some idea of this in Key Stage 1. 

In Year 3 children also need to learn the 3, 4 and 8 times tables. There will be elements of this which require some rote learning or at least rote practice to give them fast recall skills. You may try a range of mental maths games as well as regular mental maths questions to help them to apply those facts so that the connections between the rote repetition and the understanding of the numbers is firmly entwined. 

In class it is helpful to revisit physical object representation when introducing multiplication and division as they will need to see the objects as groups, and may practise ‘sharing’ among friends or dividing up resources such as pencils for each table. How many pencils do we have? How many children sit on each table? If we share the pencils equally to each table will everyone get one? Will there be any spare? 

All these questions can form part of not just a maths lesson but an opportunity to get some maths application practice when handing out pencils for a different subject too. It is vital in Key Stage 2 that children keep building on their application of maths to real world examples as then they will not seem as abstract when such questions are in a SATs paper later on. 

Mental maths skills within fractions and decimals

Children should understand, before decimal places and fractions are introduced, the true value of numbers. It is the understanding of what is being represented, both by single digits and columns of place value, that children can grasp working with numbers in a variety of ways.

If children have grasped that sharing something into five groups is division and represents breaking down a number into smaller chunks/groups, they can then apply that to their understanding of decimals and fractions. Finding a fifth of a number, for example, is akin to sharing something between five people. So a fifth of a cake, or a fifth of 20 sweets, can all be treated in the same way as standard division.

Physical representation may be used again and showing in Base 10, for example, that a ten is made up of ten ones, which can then be divided into 2 groups of five, and that those two groups of five still make ten, will help to visualise that as ½ of ten. Modelling that relationship with physical and pictorial representations on the board, or when working with small groups, will strengthen their ability to do the same mentally and can build children’s fluency with numbers. 

How mental maths skills influence children’s problem solving

It is vital that children are given many opportunities to apply their mathematical skills to a range of problems. These may involve word problems which relate to real world scenarios such as paying for items at a shop and working out the change you are due. Mental maths practice often comes naturally in these scenarios, as well as being very useful for reducing the working memory required to complete the problem solving. 

Problem solving where children do not have good mental recall of number facts can be detrimental to their confidence, but inversely when they feel confident with their known facts this can help them hugely with solving something they thought was too hard. A range of low threshold, high ceiling type tasks (where there are many possibilities but some ways of solving the problem will be more efficient) can help children to explore more complex problem solving, such as all possibilities problems. 

Children should also be approaching word problems in a variety of ways so some problem solving may be asked verbally or included in role play, such as a shop set up in the classroom or the home corner in a continuous provision environment. Questions such as “How many items can we buy? And how much will it cost?” can help children to practise their number association and addition facts. 

The complexity of problem solving will increase as children gain confidence and should always give them a chance to recall from everything they have learnt so far across all four operations, and in line with the National Curriculum expectations of the year group. National curriculum progression year by year is based on a ‘typical’ development but if there are any number facts which have not been retained or which individuals are struggling with, it is important that reasoning and problem solving does not exacerbate any misconceptions or affect a pupil’s confidence.

How to teach the key number facts and mental strategies year by year 

Mental maths year 1 

In Year 1 children should be able to recall one more and one less than any given number, although there is no requirement to specifically test any such skill formally at this stage. You would hope they are starting to recall some number facts such as the bonds to 5 or even 10, but they may still be using a lot of visual representation through to Year 3 to support their maths.

Mental maths year 2 

In Year 2 children are expected to know their number bonds to 20 and to recall them and apply them to simple word problems. In the KS1 SATs tests there will still be a lot of visual representation as they will often not be able to read a lot of text independently yet, so we do not want their maths to be hampered by their reading. By the end of Year 2 they should also be able to recall times tables facts for the 1, 2, 5, and 10 times tables. 

Read more: Mental Maths Year 2

Mental maths year 3 

In Year 3 children will learn the 3, 4 and 8 times tables and then be able to use multiples of 2, 3, 4, 5, 8, 10, 50 and 100. They should be able to apply their place value knowledge to partition larger numbers and then apply their number bonds and times tables knowledge to questions involving these multiples. They should be adding and subtracting up to 3-digit numbers and hundreds, using formal written methods but also applying their mental maths skills to these calculations for the sake of fluency and speed. 

Read more: Mental Maths Year 3

Mental maths year 4 

In Year 4 pupils will learn the 7, 9, 11, and 12 times tables and be expected to rapidly recall all maths facts in the 1-12 multiplication tables ready for the times tables test at the end of the year. They will also be multiplying by 25 and 1,000. They will be using negative numbers and counting backwards through zero with increasing fluency. Written methods will start including 4-digit numbers and their mental maths skills will be vital to ensure they are able to check the accuracy of their answers by applying inverse operations. 

Read more: Mental Maths Year 4

Mental maths year 5 

In Year 5 children will be working with numbers to 1,000,000 which makes their place value knowledge even more crucial. Mental maths skills and recall of times tables, addition and subtraction facts will help them to calculate increasingly difficult problems. They will continue to partition and also become more flexible with their preferences when working out problems mentally.

Read more: Mental Maths Year 5

Mental maths year 6 

In Year 6 children will be working with numbers to 10,000,000. Pupils should be able to apply their multiplication tables, and other known number facts to a wide range of reasoning and multi-step problems. They should be able to easily move between the four operations and calculate many steps in their head. They may use jottings to help them with larger numbers, to jot down answers to each step or within a step when partitioning for example. But they are not always using formal written methods which can take up valuable time in a test situation. 

Read more: Mental Maths Year 6

How to know when a child is secure enough to move on?

Supporting understanding 

As you move through the introduction of different maths facts and concepts across the four operations, applying them in a variety of ways teachers should spot the children who may know through memorisation, but are less able to be flexible with numbers. In this case, they may need additional support or intervention to deepen their understanding. This can mean going back to physical or visual representation of those numbers before then building up the recall through maths problems which check their mental arithmetic skills. 

Likewise look for children who seem to understand the concepts during a specific lesson – i.e. you are teaching subtraction and using manipulatives, they are able to work out the answers on some maths worksheets but cannot quickly recall many facts mentally. 

These children may need additional help and are showing that something has not ‘clicked’ in terms of their full understanding and/or fluency with number facts taught so far. It may be that they have misconceptions or that their working memory is hampered by slow recall which needs more repetition and practice.

Children who can recall easily and seem confident on single digit numbers, but then struggle with calculating two-digit numbers may lack security in place value. If they are easily recalling times tables but really struggling to use this in formal written methods it should be clear then that place value is an issue if their answers are wildly off the mark. 

Signs your mental maths is on track 

Children who are confident and secure in their maths knowledge, to the expected level in each year group, are able to make connections easily and apply their maths knowledge to a range of questions. You will also notice these students start to ‘play’ with numbers and operations. They are able to explain how they found an answer and can show you that they can check their answer by using the inverse operation. 

Early intervention is key to ensuring that children do not hit stumbling blocks with maths, and to ensure they are building their maths repertoire over time, ready for Year 6 SATs and moving to secondary school. 

Regular mental maths test question practice, and some regular low stakes written tests to assess their recently taught maths skills alongside recall from previous learning, can help to keep checking for understanding. Gap analysis of the commonly incorrect questions can feed directly into teaching so that whole class intervention is also swift. Individuals and groups can also then be given extra support or tuition as needed.

At Third Space Learning, we understand that students have different gaps in their understanding, and learn at different speeds. That’s why our one-to-one online maths tuition is tailored individually to each child’s needs, helping them to build fluency and confidence in maths. Our weekly sessions provide students with opportunities to grow their understanding of number facts and apply them across a range of questions. 

Ahead with mental maths

Crucial to the development of your pupils’ mental maths skills is your confidence that you know what to teach at each stage of their maths journey and why. Hopefully this article and those on mental maths strategies and teaching mental maths by year group, can provide you with a few straightforward tips and resources to help you to make a world of difference in children’s outcomes.