What Is Numicon? Explained For Primary School Teachers, Parents And Pupils

Numicon shapes have become a staple of the primary classroom, in part due to the popularity of the concrete pictorial abstract approach (CPA). They are an excellent multi sensory approach that supports early numeracy by helping pupils to understand the relative size of the numbers 1-10. 

However, Numicon shapes can also be used to represent numbers larger than ten. Although as a teaching resource they are a common sight, particularly in Key Stage 1, they are much more versatile approach to maths manipulatives than a lot of teachers give them credit for.

In this blog, we will explore Numicon and a variety of different topics that they can be used to teach right from Early Years through to upper Key Stage 2.

What is Numicon?

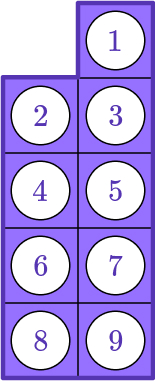
Numicon is a teaching resource developed by Oxford University Press that comprises a number of plastic shapes that represent the numbers 1-10 and are relative in size to one another. 

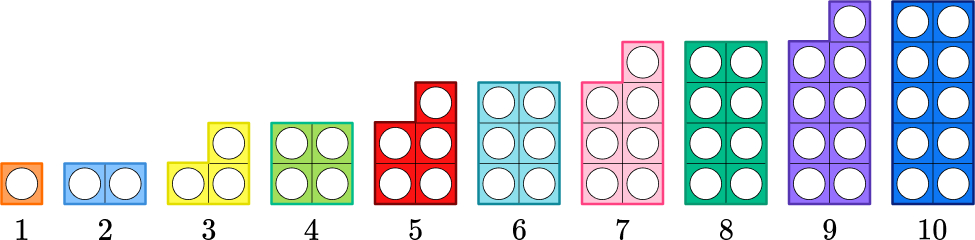
As you can see from this image, the Numicon 2 is the same size as two Numicon 1 pieces, and so on. This allows pupils to understand the relationships between numbers.

A full teaching pack of Numicon may come with a number of different items:

• Numicon Shapes: the plastic shapes as shown above which represent the numbers 1-10.
• Numicon Baseboard: a pegboard that the Numicon shapes can fit on to – the holes on the shapes fit into the pegs.
• Numicon Baseboard Overlays: picture cards that fit onto the baseboard to help children to form different numbers.
• Numicon Pegs: small coloured close-ended beads which fit onto the pegs in the baseboard to help children to ensure they count the Numicon correctly.
• Numicon Number Line: a traditional number line but with Numicon shapes pictured alongside the numerals.

How does Numicon work?

Numicon gives pupils an idea of what the value of each number looks like and that when we count in ones, the number gets bigger by the same amount each time. 

In the case of Numicon, we add an additional hole every time. It appeals to children’s visual understanding and their sense of pattern.

Numbers are a very abstract concept and, as such, pupils can often feel overwhelmed when first learning maths. This can lead to anxiety around the subject throughout their lives. 

By having a physical material that they can hold and manipulate, pupils are more likely to be able to make the connections that allow them to work with numbers in an abstract form.

This is the basis of the concrete pictorial abstract approach – pupils work with a concrete (physical) object, before making this into a pictorial (drawn) representation and then moving onto the abstract form (numerals and calculations).

Generally, pupils will go through four stages with Numicon in order to master number and the concepts that they are being taught:

• Pattern: pupils find patterns or similarities and differences in the shapes.
• Ordering: ordering the shapes from largest to smallest and smallest to largest.
• Counting: counting each hole one by one – this gives the pupil a knowledge of what each piece represents
• Early calculating: using the pieces to perform simple calculations e.g. putting a two and a three together and seeing that this is the same shape as (therefore equal to) the five.

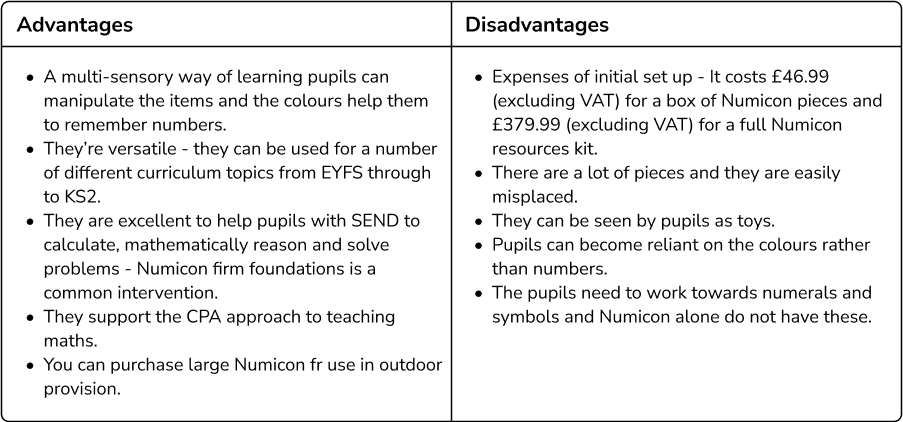
Advantages and disadvantages of Numicon

While there are several advantages to using Numicon as a teaching tool in primary schools, there are also some potential disadvantages to consider.

How to use Numicon in the classroom

To maximise the benefits of Numicon as a teaching tool, it’s important to understand how to utilise it effectively in the classroom and prepare worksheets in advance to incorporate it into your lesson plans.

1. Numicon for number recognition

It is a good idea to introduce Numicon to pupils for the first time when you begin introducing numbers to them in early years. As many EYFS teachers take each number individually, you can introduce each Numicon piece at the same time. 

Using Numicon alongside other concrete maths resources such as tens frames, number lines and counting apparatus, such as dienes, can help pupils to develop a firm understanding of numbers and an array of tools to help them when reasoning and problem solving. 

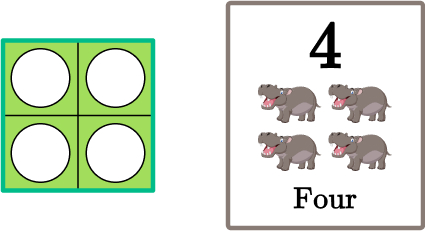
One Numicon activity that can be done to help support number recognition among pupils is to provide them with a range of Numicon pieces along with number flashcards.

The pupils simply have to match the Numicon with the number it represents. 

2. Numicon for learning to count

There are two common ways that young children can use Numicon to learn to count.

The first is simply to place a Numicon shape on the baseboard and use the Numicon pegs to fill each hole, counting using one to one correspondence as they do. 

When done under the supervision of an adult, this can confirm that a child is counting in sequence.

The second is ordering the pieces from smallest to largest. 

Once children have done this, they have made their own number line and can add the numbers underneath with flashcards or, if they are outside, use playground chalk.

3. Numicon for place value

Numicon can be very helpful for pupils exploring numbers above ten. 

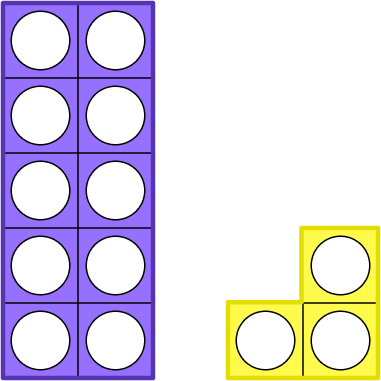
Here, we have created the number 13 using Numicon shapes. The pupil is likely to be familiar with counting to thirteen and can happily tell you this. They may also be able to write 13 in numerals. 

However, what does the ‘1’ represent in the number 13? From this representation, they can see that there is a ten and a three, therefore the 1 must represent 10 and not only 1.

In English, the numbers 13-19 are not ‘ten’ numbers but ‘teen’ numbers. By using a representation such as the one above with Numicon, pupils can understand what that means.

4. Numicon for addition

Numicon shapes can help pupils to learn to add by allowing them to place two shapes together and then either count the holes or compare with the other shapes to find the answer. 

This can be particularly helpful when pupils cross the tens boundary.

If we take 7+5:

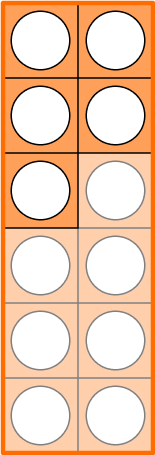
Initially, the pupil has taken a Numicon 7 and a Numicon 5 and placed them together to create a rectangle – this is encouraged with Numicon because the shapes are either rectangle or rectilinear with one odd piece. 

From this point, the pupil could place the Numicon in this arrangement on a baseboard and use pegs to count the total. 

Alternatively, they could just count the holes by pointing into each one.

However, pupils should be encouraged to move onto finding out the answer using a combination of a Numicon 10 and another shape. Usually, pupils would line the Numicon on top of one another to check that the two representations are equal. However, they can also show this side-by-side:

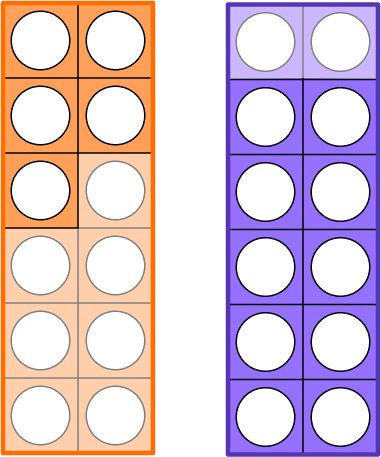
Here, they can see that 7+5 is the same as 10+2 which by this point they are likely to know is equal to 12.

5. Numicon for subtraction

Like addition, Numicon is an excellent resource for early subtraction too. It is also a great tool to help pupils to subtract crossing the tens boundary. 

As pupils have often had a lot of practice in making numbers above ten at this point, the initial starting point should be familiar with them – they simply use the Numicon shapes to make the number. 

For example, 13-5:

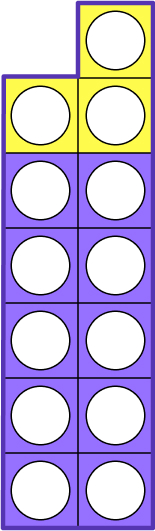
The pupil would first use a ten and a three to represent the number 13.

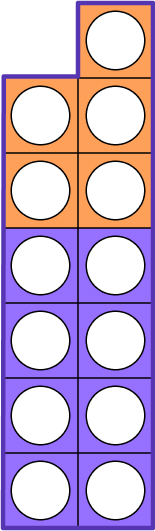
They would then take the five piece and place it on top of their number. At this point, try to encourage pupils to line up the odd pieces where relevant to help them to see the patterns being made. 

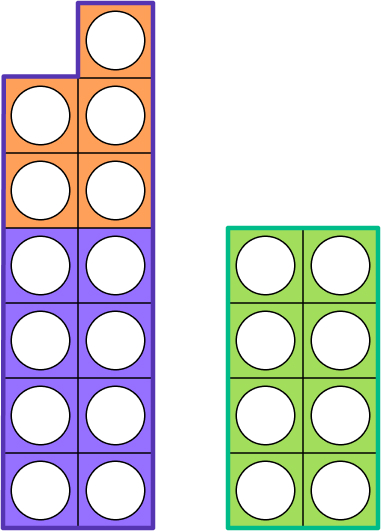
They can then either count the holes left on their original shape (as this would be 3D, they would easily tell the difference by its thickness) or find the shape that fits into the space on the original and subitise from there.

Read more: What Is Subitising?

6. Numicon for number bonds

In a similar way, pupils can use stacking to find the different ways to make number bonds for all numbers up to 10. 

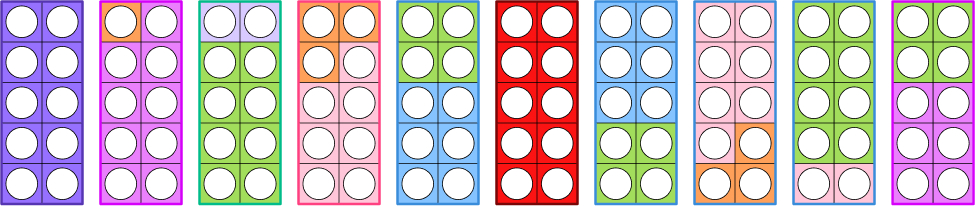
In the example above, the pupil has been investigating number bonds to 10. They have initially chosen a Numicon 10 as their base example. 

They have then used two pieces of Numicon to recreate the same shape. A natural progression from this for pupils who find this easy would be to then try to find number bonds with three addends. 

7. Numicon for times tables

As Numicon is excellent for creating patterns and numbers in different ways, it is great for helping pupils to find the multiples of a given number and therefore to learn their times tables. This is an excellent use of Numicon for Year 2 (2, 5 and 10 times tables), Year 3 (3, 4 and 6 times tables) and Year 4 (6, 7, 9, 11 and 12 times tables).

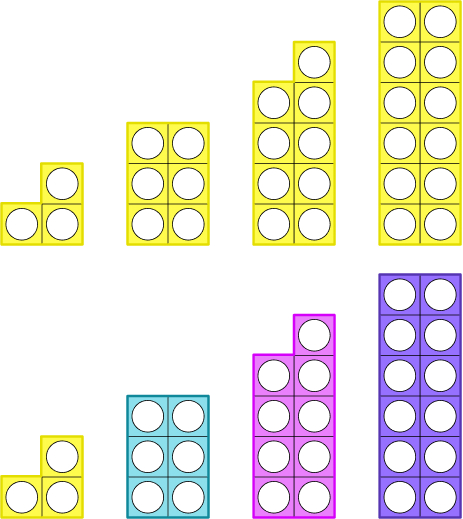
In this example, pupils are exploring the three times table. 

In the top row, they have used Numicon 3 pieces to create shapes representing 1×3, 2×3, 3×3 and 4×3. They have then found the corresponding piece of Numicon and placed it in the second row to find the multiples of three: 3, 6, 9 and 12. 

This helps pupils to understand why 2×3 is equal to six as they can visually see the two sets of three being placed together and this being the same shape as the Numicon 6.

8. Numicon for fractions

As mentioned previously, each square and hole on a piece of Numicon is of an equal size. This therefore makes Numicon a good resource for making fractions.

Initially when introducing fractions, pupils can use the Numicon shapes to represent the denominator of the fraction and then place pegs into the holes to show the numerator, therefore ‘filling in’ the fraction that is given.

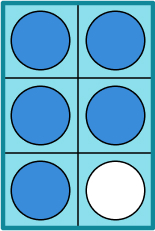
\frac{5}{6} is represented here with the Numicon 6 showing the denominator and the pegs representing the numerator.

This then leads on to being able to think about making a whole. In the example above, if the whole is 6/6 as represented by the Numicon shape, and \frac{5}{6} is represented by the pegs in the shape, then to complete this must be the number of holes without a peg – \frac{1}{6} . 

This can lead onto the calculation \frac{5}{6} + \frac{1}{6} = \frac{6}{6} (or 1)

Children can also add fractions with the same denominator using Numicon, even crossing to numbers larger than 1 from year 4.

Here, the children have been tasked with the calculation \frac{3}{5} + \frac{4}{5} .

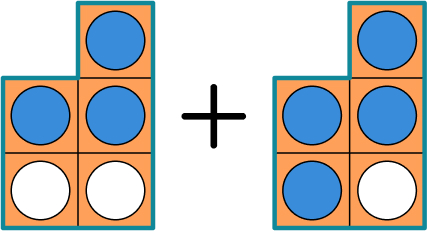
First, they have created both fractions as described above, using the Numicon shapes as the denominator and the pegs to represent the numerator. 

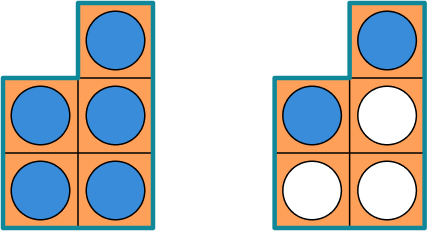
By then moving the pegs to complete the first Numicon shape, they can see that the answer has 1 whole and 2 extra fifths, therefore \frac{3}{5} + \frac{4}{5} =1 \frac{2}{5} .

9. Numicon for geometry and measurement

Numicon has also been found to be useful for measurement and geometry.

In Early Years, children can use Numicon (or any other manipulative resource) as a non-standard unit of measurement and compare the length or height of items to these. This is an excellent way to encourage children to use language such as bigger, smaller, taller and shorter. 

When introducing perimeter to year 3 children, it can be helpful to use Numicon initially as they are comfortable with it as a manipulative and therefore they have one less part of the maths to worry about. 

As the squares are clear on a Numicon shape, it can be easy to count around the edge to find the perimeter.

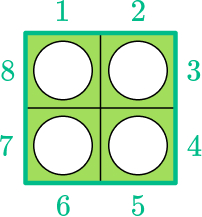
Here, the child has found out that this square has a perimeter of 8 squares. When they are comfortable with this, they can then think about working out the length of each side and adding them together:

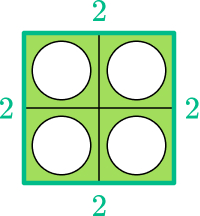
Here they can see that each side of the shape is 2 squares in length, therefore the perimeter is 2+2+2+2=8 squares. Some children may then be able to theorise that for a square, you only need to measure one side and multiply the answer by 4. This could be an excellent area for investigation.

Exactly the same process could be followed for rectilinear shapes in Year 4.

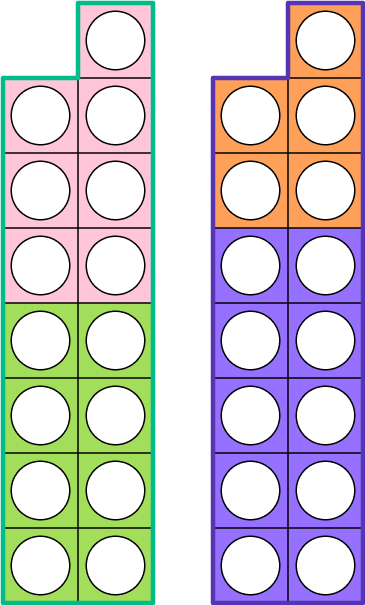
In Year 4, children also learn to measure area for the first time and they only need to learn to ‘find the area of rectilinear shapes by counting squares.’ This means that Numicon lends itself perfectly to this part of the curriculum. The children simply have to count the squares (or the holes) of the Numicon to find out the area.

This means that they can then investigate different shapes with the same area by using several Numicon pieces to make them.

When do children use Numicon in school?

Children often use Numicon during EYFS and Key Stage 1. 

However, as seen above, there are definite benefits to using Numicon when introducing new mathematical concepts to learners at KS2. The fact that they are familiar with Numicon from KS1 means that they can focus on their new maths skills rather than the manipulative that is being used.

Numicon worked examples

1. 8+7

Here the child has used a Numicon 8 and a Numicon 7 and placed them together to create a new shape, making sure the odd one is at the top. They have then used a ten and a five together to make the same shape. Therefore, they can see that the answer is 15.

2. How many different ways can you make 4?

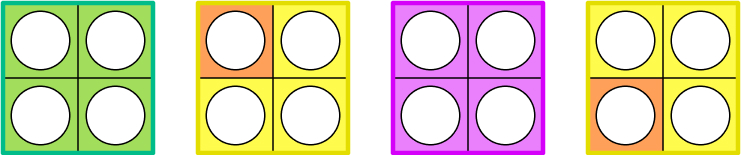
The child has taken a 4 piece and used two of the other pieces to make a shape that matches. However, you may see some of the more confident mathematicians beginning to use more than two shapes:

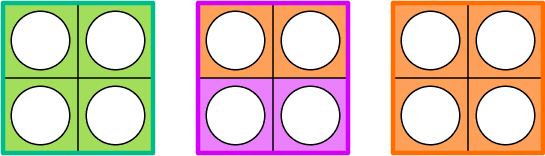
3. What is the perimeter of this shape in squares?

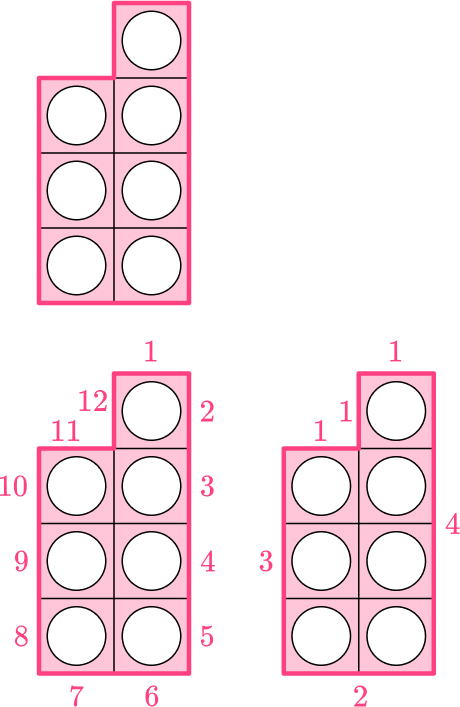
Children have two options for this question. Either they can go with the image on the left and just count each square to find the perimeter of 12 squares. Alternatively, they can measure each side separately and use addition (1+4+2+3+1+1) to also get the answer of 12 squares.

Numicon practice questions

Activity sheets are a popular format for presenting Numicon practice questions, as they allow children to work independently or in small groups to practise their skills.

1. How many different ways can you make the number 7 using Numicon?

Answer: 6+1, 5+2, 4+3, 3+4, 2+5, 1+6. 

Children may then explore with more than two pieces for which there are many answers.

2. 16-9

Answer: 7

3. Find all of the multiples of 4 to 40 using Numicon.

Answer: 4, 8, 12, 16, 20, 24, 28, 32, 36, 40

4. 4/7 + 6/7

Answer: 10/7 or 1 3/7

5. What is the perimeter of this rectangle in squares?

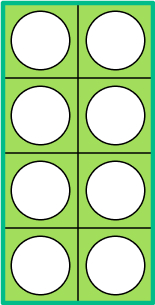
Answer: 12 squares.

Looking for more information on concrete resources for the primary classroom?

• Rekenrek
• Hundred square
• Number square