Fractions For Kids: A Comprehensive Guide For Primary School
When it comes to teaching fractions for kids at school or at home, it’s a topic that children will probably struggle with most. With words like numerator, improper, vinculum and others making their way into homework and school reports, sometimes even the number of terms relating to fractions for kids can all seem a little overwhelming for parents and teachers.
Knowing how to teach children fractions at home can just be difficult. But having taught in schools and in homes, we’ve been there and done it and can reassure you now – there is a way through, you just have to take it step by step with practice fraction questions.
- Fractions in a nutshell
- What do children need to know about fractions in KS1 and KS2?
- How to help teach children fractions in KS1
- How to help teach children fractions in Year 1
- How to help teach children fractions in Year 2
- How to help teach children fractions in KS2
- How to help teach children fractions in Year 3
- How to help teach children fractions in Year 4
- How to help teach children fractions in Year 5
- How to help teach children fractions in Year 6
Fractions in a nutshell
We understand that fractions can be frustrating for everyone, so here’s everything you need to know about them in brief!
Understanding and Comparing Fractions Worksheets
Download these FREE understanding and comparing fractions worksheets for Year 3 pupils, intended to help pupils independently practise what they've been learning.
Download Free Now!What is a fraction?
A fraction is a part of a whole. Fractions are used to represent smaller pieces (or parts) of a whole.
The parts might make up one thing, or more than one thing. Either way, altogether, they make up what’s called a whole. You can have a fraction of a number for example 2/3 or 9 or a fraction of an amount for example 2/3 of a pizza.
It’s important to note that a whole can mean more than one thing. It’s useful to think of a sweet shop as an analogy. For sharing a singular whole amount, you can think of a chocolate bar, a cake bar, or muffin. For grouping an amount into fractional parts, you can imagine a bag of sweets – there are lots of sweets in the bag, but you need all of them to make up the whole bag.

Unlimited primary maths tutoring with Skye, the voice-based AI maths tutor.
Built on the same principles, pedagogy and curriculum as our traditional tutoring but with more flexibility, reach and lower cost.
Join the schools already helping hundreds of primary pupils nationwide with Skye’s one to one maths tutoring
Watch Skye in actionWhat is a child friendly definition of a fraction?
A simple definition of a fraction for children is:
A fraction is any part of a group, number or whole.
What are the parts of a fraction?
A fraction has three parts. They are:
The numerator which is the number above the bar.
The denominator which is the number below the bar.
The vinculum which is the bar separating the two numbers.
What is a unit fraction?
A unit fraction with 1 as its numerator (top number), and a whole number for the denominator (bottom number).
Read more: What is a unit fraction
What is a non-unit fraction?
A non-unit fraction is a fraction with a number greater than one as its numerator (top number) and a whole number for the denominator (bottom number).
Read more: What is a non unit fraction
Using objects to visualise fractions
When you’re starting out with teaching children fractions, objects or pictures of objects are a great way to understand how they work.
Start with concrete items, like food or counters – you can use pasta pieces or dried beans in place of counters – then draw them as pictures.
Once you’ve got this down, you can move onto using rational numbers (the fancy name for fractions) to represent them. Learning fractions in this order makes it easier to work out fractions of natural numbers later on.
The most important thing to remember when you’re dealing with fractions is to go slow.
There’s so much information to process! Even if something seems easy, take the extra time to really understand the basic concepts behind fractions. It will make life a lot easier when you come to more complex problems that involve converting between fractions, decimals and percentages later on.
Examples of fractions in everyday life
- Splitting a bill at a restaurant into halves, thirds or quarters
- Working out price comparisons in the supermarket when something is half price
- Figuring out amounts in the kitchen, for example a recipe could serve 10 people but there are only 4 eating, and this means you’ll need fractions to figure out the correct amount
- Adding up monetary amounts
- Looking at time! Half an hour and quarter past are both common things to hear where time is concerned!
Why are fractions so tricky in primary school maths?
In the first years of school, you learn how numbers work. You learn how to count, and that the number 1 is equal to one object, 2 is equal to two objects, and so on.
You learn that when you count up, the numbers have more value. And then, just when you think you’ve got the hang of numbers, you learn that there are other types of numbers out there, like fractions.
As a child, you are still making sense of the world. So when you learn a set of rules (like how to count with positive whole numbers), you hold onto them. The problem? When you come across things that don’t fit the rules, it’s much harder to understand.
Positive whole numbers (like 1, 2 or 65) are simple. They gain more value as they go up, and they always mean the same thing (1 always means 1, and 2 always means 2). They are also known as natural numbers. Fractions are known as rational numbers, and they follow different rules.
To cut a long story short, understanding how to do fractions can be tricky for primary school children.
Fractions don’t always mean the same thing. ½ of a cake is not the same as ½ of three cakes, or ½ of a bag of 12 sweets! That’s the first hurdle – the value of a fraction changes depending on how big the numerator (top number) is. Secondly, if the bottom number (the denominator) in a fraction gets bigger, the value decreases. On top of all of that, names for fractions don’t always sound like the number they represent, like an eighth for ⅛ or a quarter for ¼.
More support for maths at home is available:
What do children need to know about fractions in KS1 and KS2?
With fractions for kids changing from year to year throughout primary school, there is a lot to cover in the blog, but to help you out we’ve broken it down on a year by year basis.
How to help teach children fractions in KS1
In KS1 almost the most important thing you can support children with is their understanding that a fraction is a part of a whole. And a unit fraction is an equal part of a whole. If they can grasp this, they can move forward.
How to help teach children fractions in Year 1
When it comes to fractions, Year 1 is all about getting to grips with the basics.
Fractions for a 5 or 6 year old is about how to use objects to find simple fractions like ½ and ¼. The good news is that you can have a lot of fun with fractions at this age!
Get creative when helping them work out fractions
When demonstrating sharing into halves or quarters, it is vitally important to show something being shared into equal parts. By doing this children will be able to visualise what is happening when you are creating the fraction, and it will help with their understanding.
Playdough is a great place to start when helping children to work out fractions at a young age, as it is malleable and easy to adapt into different fractions.
However, a firm favourite in primary classrooms is using food to represent fractions, and this is what you can do with your child at dinner time if pizza is on the menu!
Remember to emphasise the importance of every slice of pizza being of equal size.

This is a simple visual representation of a fraction, and you can adapt it to try it with ¼ too.
You can use any food that’s easy to dede up, but make sure to use the language of fractions while you do this (halves, quarters and divide).
The numbers children will be working with for Year 1 fractions
In Year 1, children will largely be focused on the numbers 0-20, but they may also work on some specific larger numbers that are easy to tackle at this age. For example, they may be able to tell you that half of 100 is 50, or that one quarter of 100 is 25.
How to help teach children fractions in Year 2
In Year 2, there’s a firm focus on finding fractions of lengths, shapes and sets of objects.
Fractions for a 6 or 7 year old involves continuing use of physical items to help them visualise fractions, so now is a good chance to crack out the counters (or a suitable replacement) for some easy practice!
They’ll also learn that some fractions are equivalent too – for example, 2/4 is the same as ½, or 2/6 is the same as ⅓.
Here’s how to explain it simply using counters (pasta or dried beans are a suitable replacement from the cupboard).

To help children fully figure out equivalent fractions, point them out wherever you can, (especially ½ and 2/4 at this stage) as this continued repetition will help them to practise until they perfect their knowledge.
Another easy way to practise is to shade in different fractions of shapes, like this:
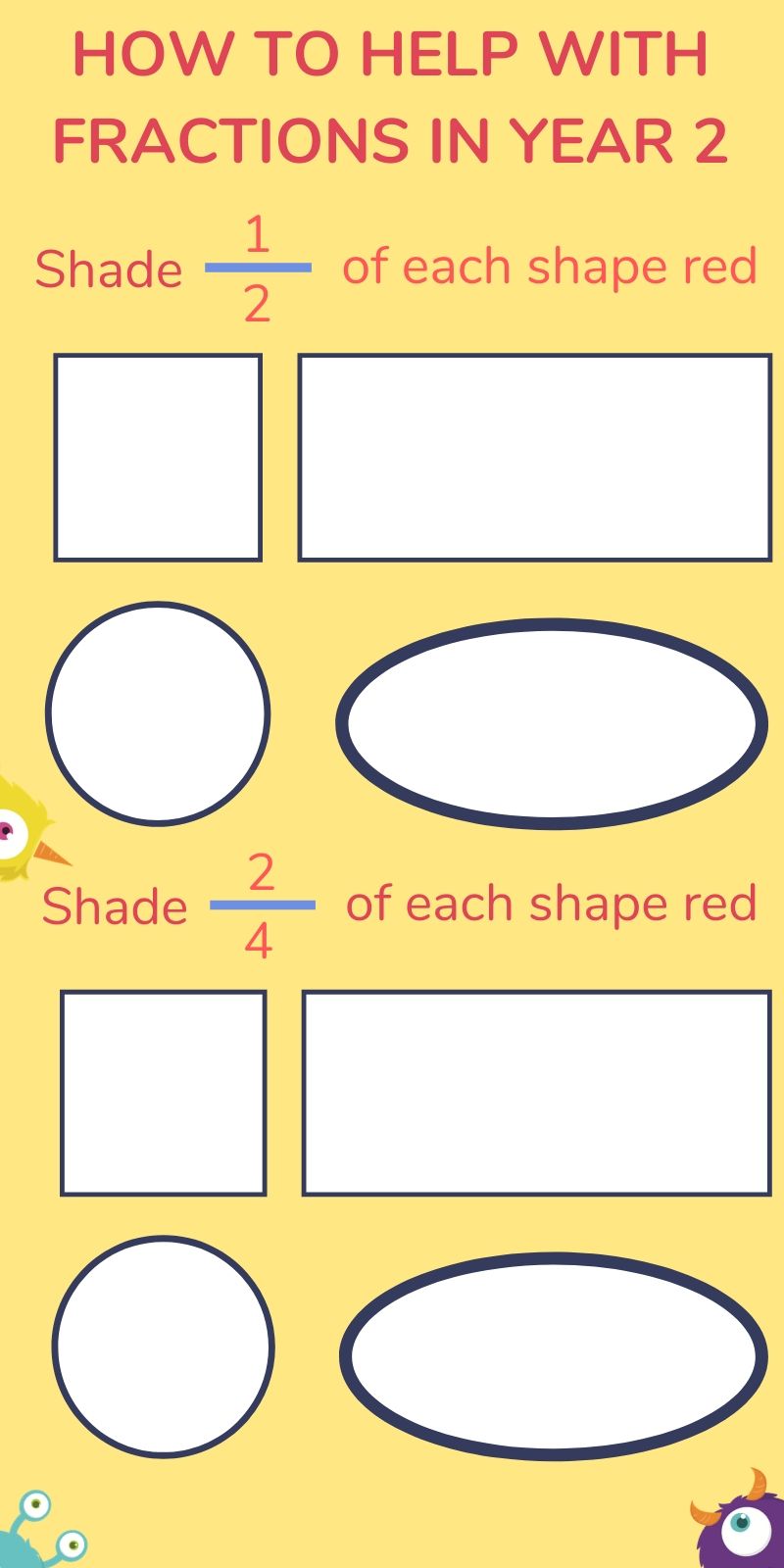
This simple, yet visual method is a great way for children to work on their fractions in Year 2.
How to help teach children fractions in KS2
KS2 is the time when fractions can get slightly tougher for children, but with all of the help on offer below, you won’t have any trouble helping them learn all about fractions at home!
How to help teach children fractions in Year 3
Fractions for 7 and 8 year old kids in Year 3 involves them starting to move away from using objects to understand fractions.
They will still use some visual aids when working with fractions, but there is more of a focus on understanding how to write fractions as rational numbers (the form you are used to seeing them in) too.
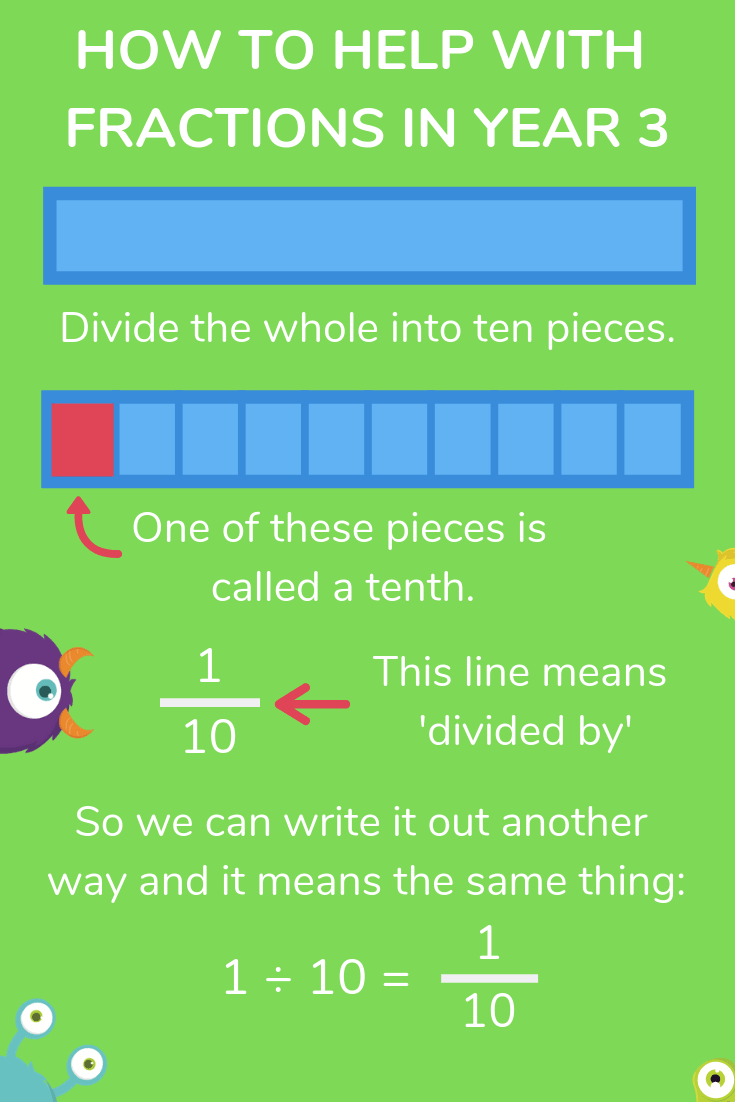
Side note… the division symbol looks like ➗ as it shows a fraction bar (or – its proper name – a vinculum) with a dot above and below it; the top dot signifies a missing numerator and the bottom dot represents a missing denominator. The division symbol itself is a constant reminder of the link between fractions and division!
Equivalent fractions in Year 3
At this age, children also need to know a few equivalent fractions with small denominators, and be able to put them in order.
Equivalent fractions is a real leap for many children, and most teachers find it a real stumbling block for many children in their classes.
However, there are three sure-fire ways of helping children understand how to do equivalent fractions in Year 3, and you can see them below!
Equivalent fraction playdough
This is a simple, yet very effective activity that can help children to visualise equivalent fractions in a way that they will understand.
How to run the activity
- Give children three evenly sized balls of playdough.
- Get them to break one ball down into halves, another into quarters and the third into eight evenly sized pieces.
- Now, use a scale – preferably a balance scale – to show that the half is equal to two quarters and four eighths. (Also, that a quarter is equal to two eighths, and that three quarters is equivalent to six eighths.)
- You could get them to reform the three original balls of playdough, breaking them down into three, six and nine equal pieces. Again, you can demonstrate that a third is equal to two sixths and three ninths, and that two thirds are the same as four sixths and six ninths.
Equivalent fraction paper strips
All you need for this activity is a sheet of paper, some scissors, and a bit of patience when it comes to cutting the strips!
How to run the activity
- Firstly, cut some strips of paper. They must be paper strips of equal length.
- Fold the first strip in half.
Fold the second strip into quarters.
Fold the third strip into six equal parts or sixths.
Fold a fourth strip into eight equal parts or eighths.
Finally, fold a strip into twelve. - Next, work with your child to label the strips, so each part on the first strip has ½ written on each part, the second strip is labelled with ¼s, and so on. Now, you / they can show that a half is equal to two quarters, three sixths, four eighths, and six twelfths.
You can then show that a quarter is equal to two eighths and three-twelfths.
You could repeat the process again, folding equal length paper strips into three, six, nine and twelve, showing that two sixths, three ninths and four twelfths are equal to a third.
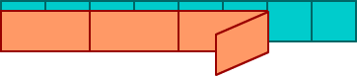
Using the strips you’ve made, you can do the same for ¾ and ⅔ too! You’re off to the races!
Comparing, and adding & subtracting fractions in Year 3
Of course, the value of a fraction depends on the numerator (the top number) and the denominator (the bottom number).
Fortunately, in Year 3, you only need to compare fractions with the same denominator, which makes things easier.
When the denominators are different, there are a few more steps to follow, which we’ll explain later on in this blog.
You’ll be pleased to hear that adding and subtracting fractions isn’t too scary in Year 3.
As the denominators are the same at this point, you just add the numerators, like this:
¼ + 2/4 = ¾
Which can be shown using paper strips again:

The principle is the same for subtraction in Year 3.
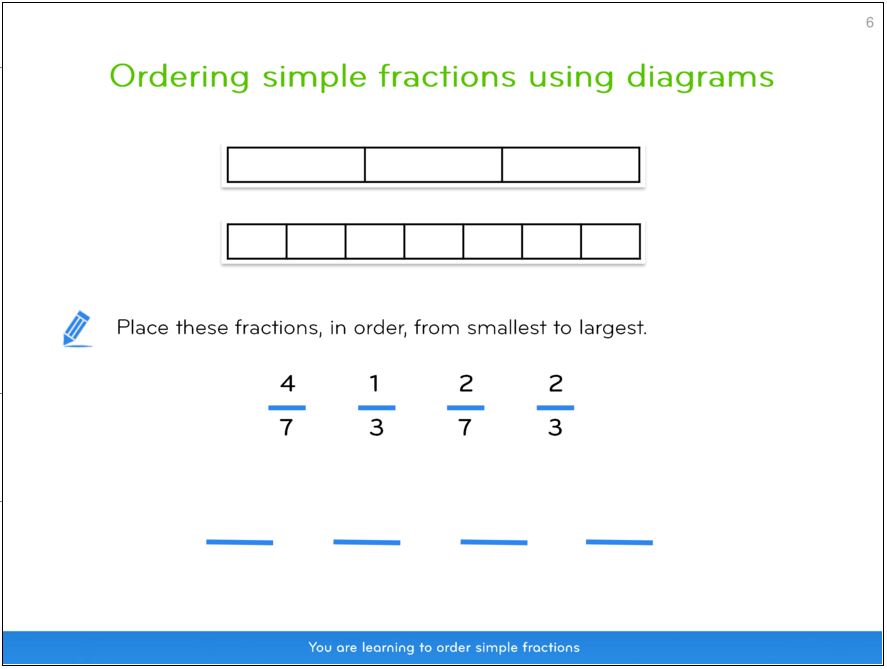
How to help teach children fractions in Year 4
In Year 4, children should be beginning to understand the basics of how to do fractions, and they will have more of a focus on using abstract fractions.
It’s likely that they won’t be using as many counters and other physical learning resources, although it is still important to weave these into their learning, meaning you shouldn’t stop practising with them at home!
Fractions for 8 and 9 year olds is about nailing the basics before everything gets a lot more complicated in year 5.
By the end of Year 4, children will need to know how to:
- Count up and down in tenths and hundredths
- Work out fractions of amounts
- Add and subtract fractions (same denominator)
- Recognise quite a few common equivalent fractions and decimals.
Fractions word problems in Year 4
At this point in primary school, word problems become more common, usually involving measurement units, like mm, cm, m, km and g and kg, and money.
Working out fractions of amounts is much easier if you use bars to represent the different parts.
Take for example the question of:
What is 1/6th of 1200m?
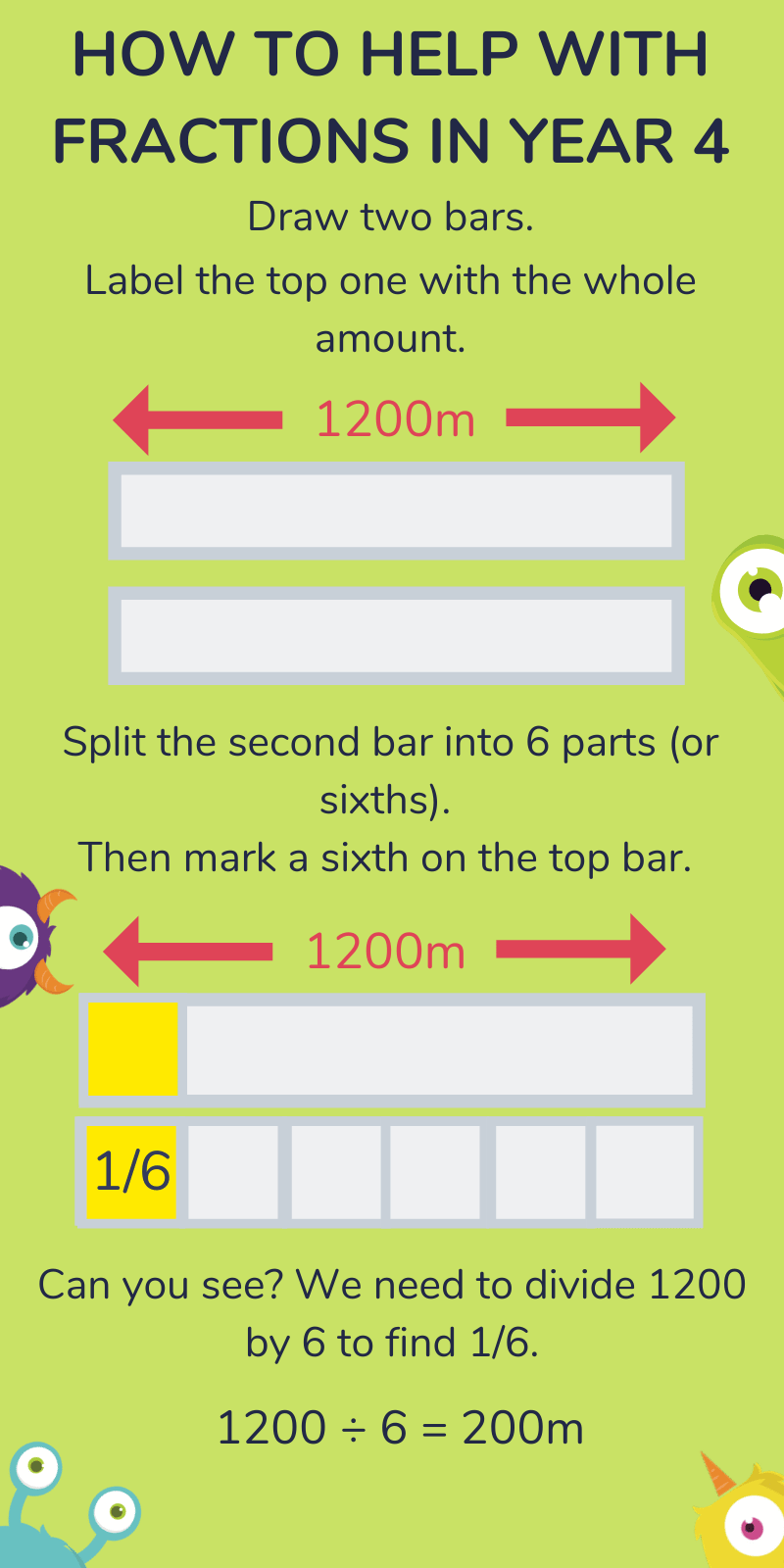
If you wanted to work out 2/6 of 1200m, you’d just multiply the answer for 1/6 by 2. For 3/6, you’d multiply it by 3.
Bars work really well for learners who like to see things laid out visually. They can be used for other areas of maths too – ranging from division, multiplication, addition and subtraction to ratio and proportion – not just fractions!
Equivalent fractions in Year 4
The word equivalent just means the same as.
In Year 4, children need to know the decimals (numbers with decimal points) that correspond to simple fractions.
You can work them out manually (by dividing the numerator by the denominator), but it’s a good idea to memorise the common ones so you can access them quickly.
| Fraction | Decimal |
| ½ | 0.5 (or 0.50 – the value is the same) |
| ¼ | 0.25 |
| ¾ | 0.75 |
How to help teach children fractions in Year 5
Year 5 is probably the most challenging year for fraction learning, and unfortunately other than hard work, there is not an easy way for 9 ad 10 year olds to learn their fractions this year.
But if you really know the concept behind fractions (that they’re parts of a whole and they have different rules to natural numbers), then you’ll be fine.
The reason that Year 5 can be tricky is that there’s very little concrete representation, A.K.A most of the pictures and items used to represent fractions are now gone!
Your child will start to add and subtract fractions with different denominators, which means there are a few more steps involved.
The language used can be challenging too.
Make sure to use words like denominator, numerator, divide, compare, order, improper fraction and mixed number often to keep key vocabulary fresh in children’s minds, as this will stand them in good stead for the work they will be doing throughout Year 5.
Comparing and ordering fractions in Year 5
Comparing and ordering fractions with the same denominators is relatively simple.
However, in Year 5, you need to know how to compare and order fractions with different denominators.

Most schools will not use the calculator strategy though, as calculators are not used in the Year 6 SATs (also known as the End of KS2 Assessments).
If children are struggling to grasp the concept of comparing fractions with different denominators though, the calculator is a good place to start.
Calculator free way to work out ordering fractions
The process of ordering fractions without a calculator may take a little longer for children to get to grips with, but it is something they will need to know in Year 5.
The image below demonstrates how to work out ordering fractions if you don’t have a calculator.
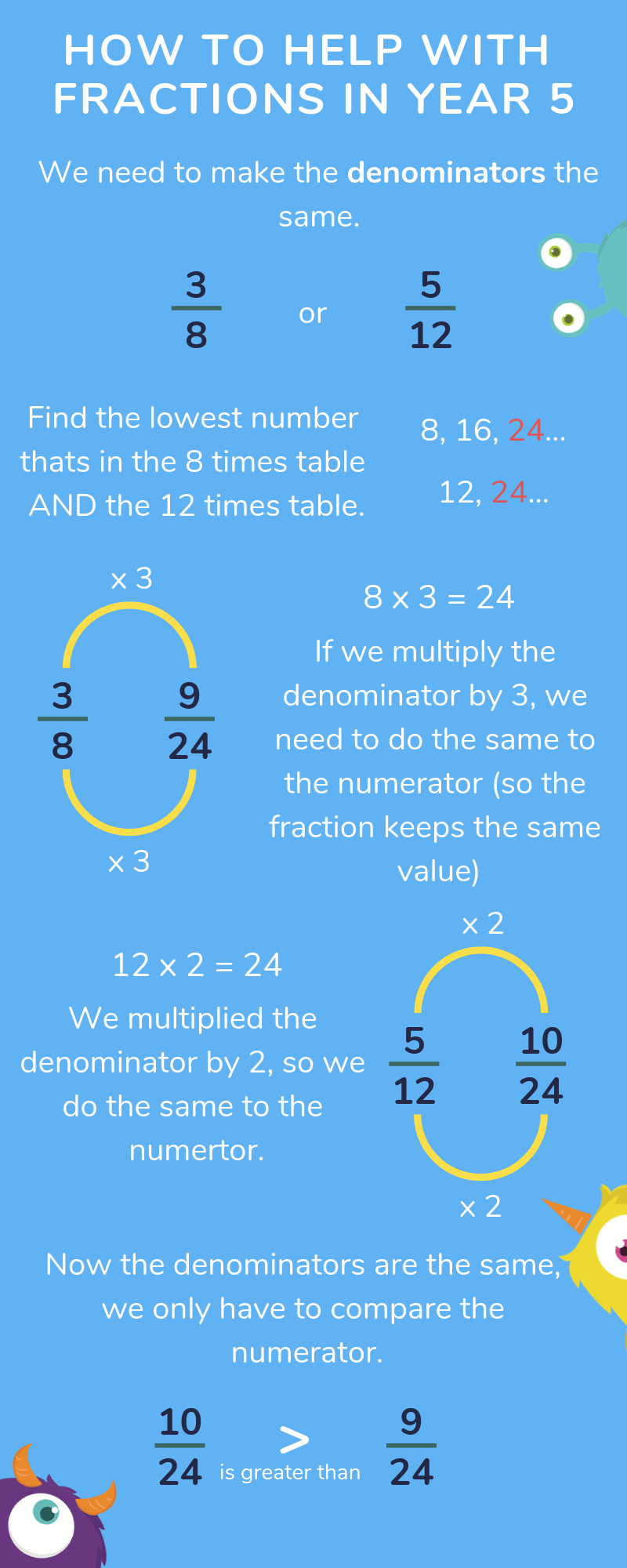
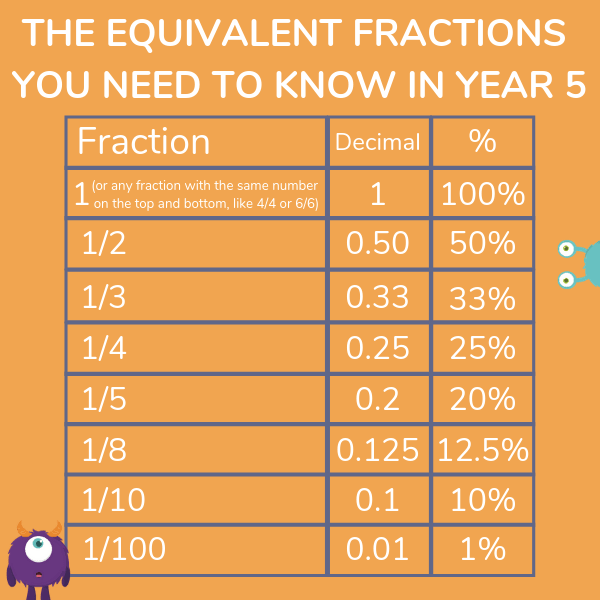
Ordering fractions can be made much quicker if you know your equivalent decimals and percentages.
Here are the equivalents you need to know in Year 5.
Mixed numbers and improper fractions in Year 5
When you have a whole number and a fraction side by side, like 1 ½ , it’s called a mixed number. You can convert this into a fraction, but the numerator will be bigger than the denominator. In this case 3/2. This is called an improper fraction (you may also hear it being called a top-heavy fraction).
Understanding how to do improper fractions is something that is important in Year 5, and it is something that you can help your child to do.

Adding and subtracting of fractions in Year 5
Another skill children will learn in Year 5 is how to add and subtract fractions.
Adding and subtracting fractions with the same denominator is simple as you just add the numerators and keep the denominators the same.
⅛ + ⅜ = 48
But, when the fractions have different denominators,they need to be made the same before you go any further.
Year 5 is a good time to get used to finding common denominators (making the bottom number the same) as in Year 6, much of the fractions work your child will do relies on their ability to do this.
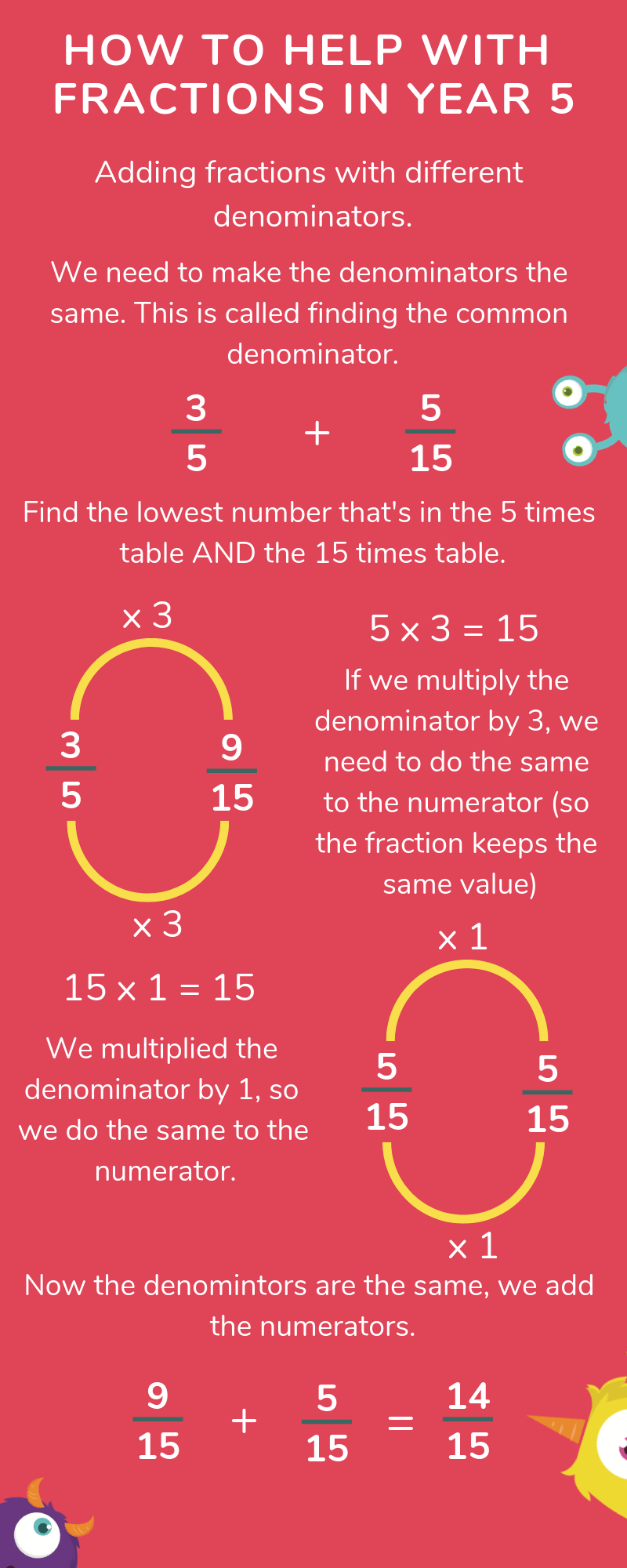
Multiplying proper fractions by fractions in Year 5
Having learned an awful lot about fractions already by Year 5, knowing how to times (multiply) fractions is relatively simple compared to all the other processes your child has learned by this stage.
You just multiply the numerators then multiply the denominators, like this:
2/4 x 3/5 = 6/20
Multiplying fractions by whole numbers in Year 5
When you’re asked to multiply a whole number by a fraction, it looks a little bit confusing to a Year 5 child. For example:
3 x 3/4
To overcome this daunting problem, you could begin by returning back to paper strips, like so:



Here it is important to remember that the denominator remains the same. If that is proving a stumbling block, you can roll out every maths teacher’s best friend: pizza.
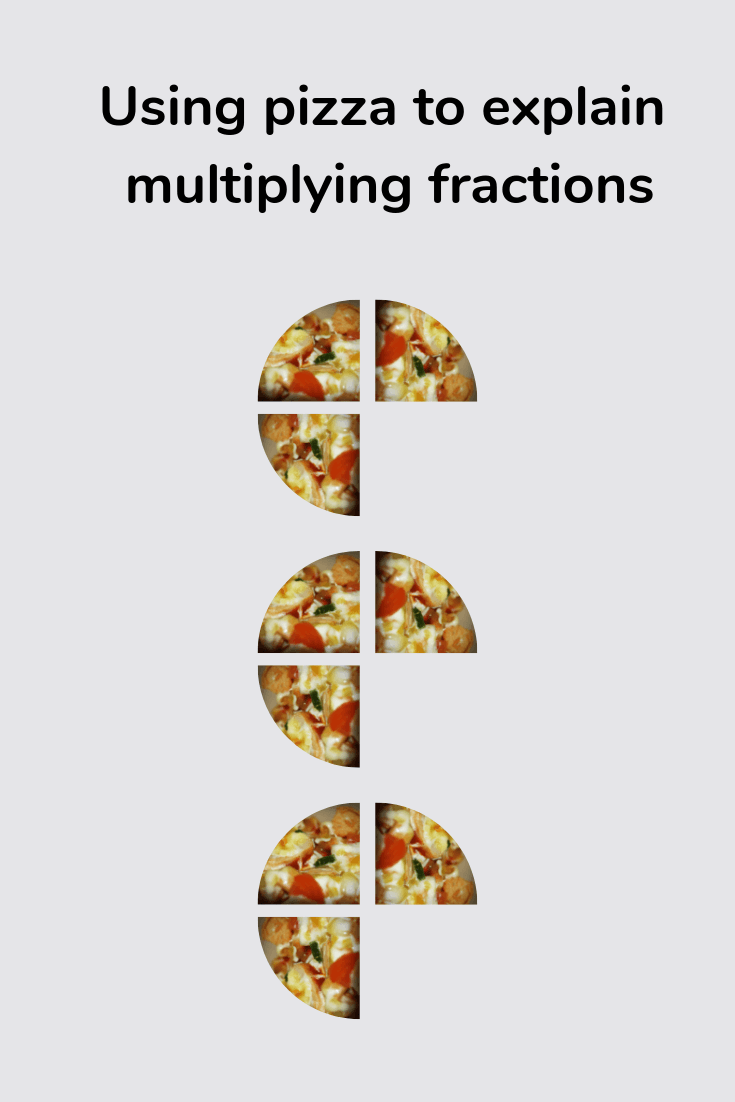
But if you remember one simple fact, it’s a lot easier.
Any whole number can be made into a fraction by giving it a denominator of 1.
3 = 3/1
That’s because 3/1is the same as 3 ÷ 1, which is 3.
The resulting equation is much easier to solve. Just multiply the numerators together, and then the denominators together.
3/1 x 3/4= 9/4
How to help teach children fractions in Year 6
By Year 6, children will have covered most of the fraction material they’ll need in primary school maths.
Although there are one or two new processes to learn, it’s important to revise the basics this year in time for the KS2 SATs in May – they always seem to come around much quicker than you’d expect!
One of the most important things to ensure children are confident with is making different the denominators are the same, as if this is the case they’ll feel a lot more sure of their abilities within the next chapter of fraction work.
It’s easy to feel overwhelmed by fractions in Year 6, but there are still things you can do to help children overcome any fractions frustration! For instance, allowing children to apply fractions to real-life scenarios such as fraction games can help break down the process by making it more interactive.
How to simplify fractions in Year 6
A new requirement in Year 6 is to write fractions in their simplest form.
This just means that we use the lowest possible numbers when we work out our fractions.
We do this to keep things simple – it stops us from ending up with fractions made up of huge numbers (which can be confusing).
Learning how to simplify fractions is another area which highlights the importance of children mastering their times tables.
For example, even though we know that 2/4 is a perfectly acceptable fraction, we simplify it to 1/2 to keep things easy (using our knowledge of the 2 times table and, consequently, halving).

You can make simplifying fractions easy by practising finding the highest common factors of pairs of numbers.
A great technique for finding factors are factor rainbows, an example of which can be seen below.
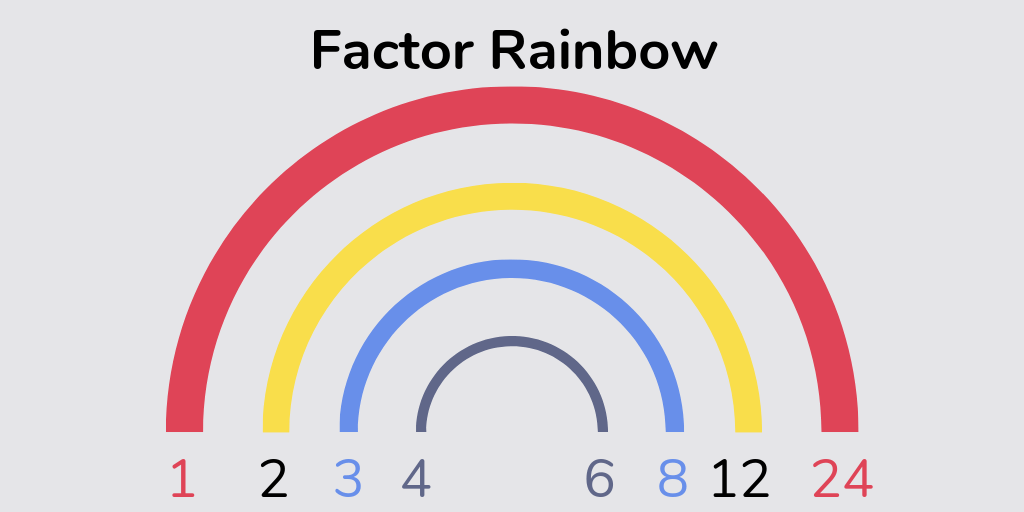
How to divide proper fractions by whole numbers in Year 6
Learning how to divide fractions is a simple process, as long as you remember that when you’re using whole numbers in a fraction problem, you can put that number over 1 to make it a fraction too, like this:
3 = 3/1
So if you’re solving a problem like 3 ¾ , turn the 3 into a fraction first.
3/1 / 3/4
Next, flip over the second fraction (turning it into its reciprocal) and change the operation to multiplication.
3/1 x 4/3
Now it’s a simple multiplication problem, just multiply the numerators and the denominators to find your answer.
3/1 x 4/3= 12/3
Don’t forget to simplify the answer! In this case, the answer will be a mixed number.
12/3= 12 / 3 = 4
Fractions, decimals and percentages in Year 6
Fractions, decimals, and percentages all represent parts, or pieces, of a whole so it’s not surprising that they’re closely related.
It’s good to know how to get from one to the other, especially when you’re ordering or comparing amounts.
Children should get to know the more common equivalents by heart (see table above) – and learn the strategies for finding common percentages.
For example, to find 1% they must divide the amount by 100, or divide the amount by 10 and the result of this division calculation by 10 again.
Converting fractions for KS2 SATs in Year 6
By the end of Year 6, children will need to know how to convert fractions into decimals and decimals into percentages.
Converting fractions into decimals
Divide the numerator by the denominator.
If they do not know their equivalences or if it is a more obscure fraction (which it is unlikely to be), they should revert to using short division (otherwise known as bus-stop division).
Converting decimals into percentages
Multiply the decimal by 100. For example, 0.79 would become 79%.
Converting percentages into decimals
Divide the percentage by 100. So, 87% would become 0.87.
Converting percentages into fractions
Put the percentage amount over 100 (e.g. 75% = 75/100), then simplify it – in this case ¾ .
Although there are written methods for converting decimals back into fractions, at this stage it’s best to focus on what’s required for the curriculum in primary school maths and for the most part simple equivalences like 0.25 being ¼ will be all that is required (knowing the eighths is helpful too such as 0.375 being the same as three-eighths).
It’s worth also reading this article on comparing fractions decimals and percentages.
Fractions in reasoning and problem solving in Year 6
In Year 6, there are two papers (Paper 2 and 3) that children will have to take as part of their SATs.
These papers are about problem solving and reasoning. Fractions will appear in Paper 1 (arithmetic) too, but they tend to be a little trickier when they’re in context.
Get children to have a go at the following SATs questions to get a feel for the kind of word problems that come up.
Follow these steps to help make them a little easier:
- Read the whole question. Check how many marks there are.
- Read the question again, circling any important information (this could be words that give you a clue to the operation needed, like halve, share etc.).
- Decide which operation you need to use (addition, subtraction, multiplication or division) and if you need to take more than one step to solve it.
- Use the operations and steps you decided on.
- Double check the answer. Does it make sense in the context of the question?
Example SATs fractions questions for Year 6
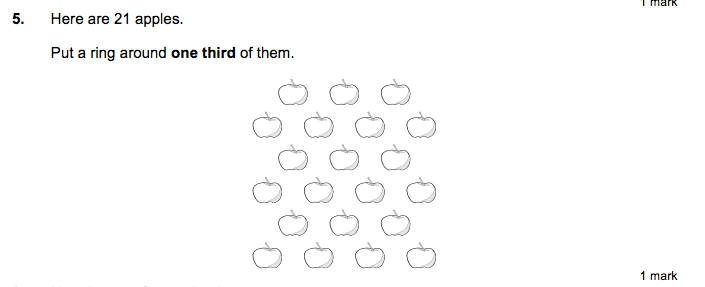
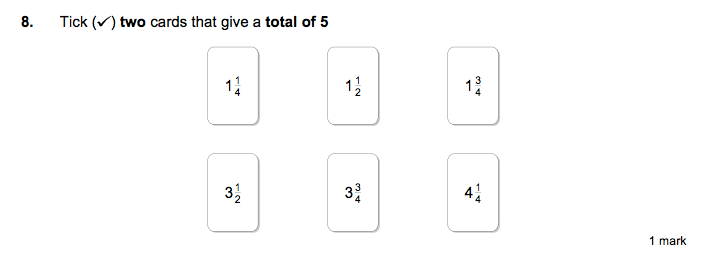
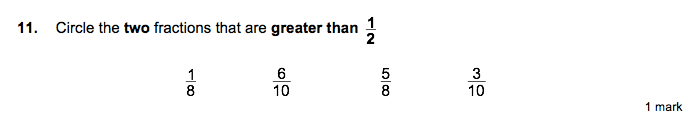
DO YOU HAVE STUDENTS WHO NEED MORE SUPPORT IN MATHS?
Skye – our AI maths tutor built by teachers – gives students personalised one-to-one lessons that address learning gaps and build confidence.
Since 2013 we’ve taught over 2 million hours of maths lessons to more than 170,000 students to help them become fluent, able mathematicians.
Explore our AI maths tutoring or find out about a primary school maths tutor for your school.