What Is A Numerator And Denominator? Explained For Primary School Teachers & Pupils

Fractions are prevalent throughout the primary maths curriculum, and understanding the numerator and denominator is vital. Children in Key Stage 2 are required to explore fractions in complex ways, so will need a foundational understanding of the different parts of a fraction.

We’ll be covering the basics around what the numerator and denominator are, with worked examples and practice questions to test your pupils’ understanding of fractions.

What is a numerator and denominator?

The numerator and denominator are the names of the two numerical parts of the fraction, above and below the dividing line respectively. 

The denominator of a fraction (bottom number) represents the total number of equal parts the whole has been split into; the numerator of a fraction (top number) represents how many of those equal pieces we have. 

For example, in the fraction \frac{2}{3} , the denominator is 3 (indicating that the whole has been split into three equal parts) and the numerator is 2 (indicating that we have two of those three parts).

As a fraction is another way of representing a division. This means that the numerator (top part) is the dividend, the denominator (bottom part) is the divisor, and the fraction itself is the quotient. 

For example, \frac{3}{4} is another notation for 3 ÷ 4 (the answer to which is \frac{3}{4} ).

Numerator and denominator examples

Fractions with a numerator of five: \frac{5}{7} , five tenths, five out of nine, \frac{5}{3}

Fractions with a denominator of five: \frac{1}{5} , three fifths, two out of five, \frac{7}{5}

Fractions with a numerator of one (e.g. \frac{1}{6} ) are called unit fractions. Fractions with a numerator of above one (e.g. \frac{2}{8} ) are called non-unit fractions. 

Fractions where the numerator is lower than the denominator (e.g. \frac{3}{5} ) are called proper fractions. Improper fractions are a type of fraction where the numerator is higher than the denominator (e.g. \frac{9}{7} ).

When do children learn about the numerator and denominator in the national curriculum?

Whilst the term ‘numerator’ doesn’t actually appear in the National Curriculum, it is almost certainly assumed that it will be taught alongside the term ‘denominator’, which is introduced in Year 3. It is then regularly referred to throughout the Key Stage 2 maths curriculum.

In Year 3, pupils should be taught to:

• Recognise, find, and write fractions of a discrete set of objects: unit fractions and non-unit fractions with small denominators.

• Recognise and use fractions as numbers: unit fractions and non-unit fractions with small denominators.

• Recognise and show, using diagrams, equivalent fractions with small denominators.

• Add and subtract fractions with the same denominator within one whole [for example, \frac{5}{7} + \frac{1}{7} = \frac{6}{7} ].

• Compare and order unit fractions, and fractions with the same denominators

• Solve problems that involve all of the above.

In Year 4, pupils should be taught to add and subtract fractions with the same denominator.

In Year 5, pupils should be taught to:

• Compare and order fractions whose denominators are all multiples of the same number.

• Add and subtract fractions with the same denominator and denominators that are multiples of the same number.

• Recognise the percent symbol (%) and understand that percent relates to ‘number of parts per hundred’, and write percentages as a fraction with denominator 100, and as a decimal.

• Solve problems which require knowing percentage and decimal equivalents of \frac{1}{2}, \frac{1}{4}, \frac{1}{5}, \frac{2}{5}, and \frac{4}{5} and those fractions with a denominator of a multiple of 10 or 25.

In Year 6, pupils should be taught to add and subtract fractions with different denominators and mixed numbers, using the concept of equivalent fractions.

How does the numerator and denominator relate to other areas of maths?

Children will need a good understanding of numerators and denominators to help them manipulate fractions in all the ways required by the curriculum, such as adding fractions, subtracting fractions (which you will need a common denominator to do so). 

It will help them learn the process of how to multiply fractions and how to divide fractions, how to simplify fractions, and also with ordering, converting, and comparing fractions. 

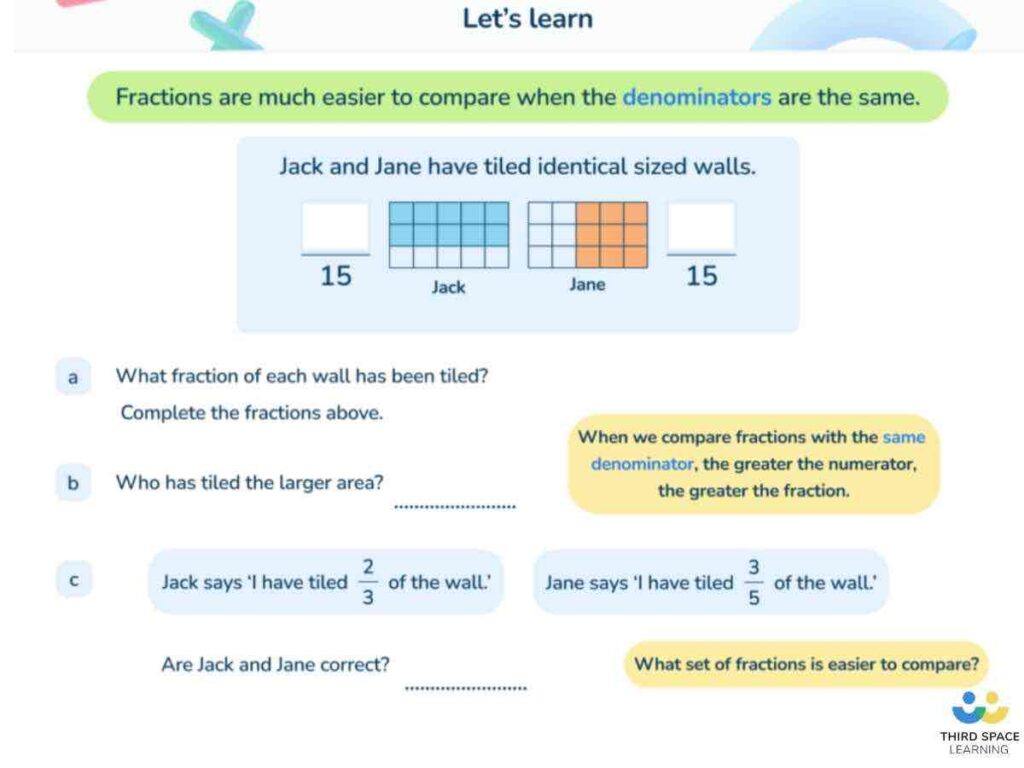
Numerator and denominators in real life

Whilst the terms themselves are unlikely to be used in real-life scenarios, fractions are used regularly in everyday life, For example:

• Splitting a bill (in halves for two people; eighths for eight people, etc).

• Working out discounts (half price, \frac{1}{3} off, etc).

• Altering recipes (e.g. using a recipe for 4 people but only cooking for 3, so adjusting the measurements by finding three quarters of each amount).

Worked examples for the numerator and denominator

1. Ben has 9 sweets and gives away 7 of them. What fraction of sweets does he have left?
   The total number of equal parts here is 9. This then becomes the denominator of the fraction. As he has given away 7, he has 2 left. This becomes the numerator as it represents the number of equal parts we have. The answer is \frac{2}{9} .

2. What fraction of this grid is shaded black?
   
   

   

   
   The total number of equal parts here is 10, which becomes the denominator. 3 of those equal parts are shaded - this becomes the numerator. The answer is \frac{3}{10} .

3. Each diagram is split into equal sections. Shade \frac{3}{4} of each diagram.
   
   

   

   
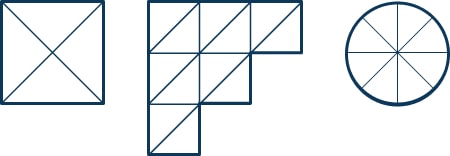
   To find \frac{3}{4} , a shape must first be split into 4 equal parts (the denominator). 3 of those equal parts (the numerator) can then be shaded.
   Shape 1: this is already split into 4 equal sections, so any 3 can be shaded.
   Shape 2: this shape is split into 12 equal sections. Once divided into 4 equal parts, there would be 3 in each one. 3 equal parts of those 3 are 9, so any 9 can be shaded.
   Shape 3: this shape is split into 8 equal sections. Once divided into 4 equal parts, there would be 2 in each one. 3 equal parts of those 2 is 6, so any 6 can be shaded.
   
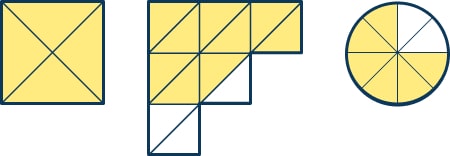
   Example answers could be:

Practice questions and answers

1. There are seven days in a week. What fraction of a week is the weekend?
   \frac{2}{7}

2. Here are some shapes made of squares. A fraction of each shape is shaded.
   Match each shape to its equivalent fraction.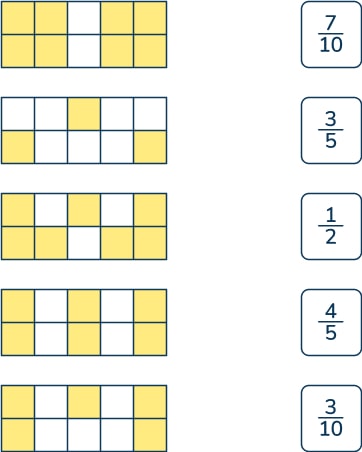
   
   

   

   
   Shape 1: \frac{4}{5}
   Shape 2: \frac{3}{10}
   Shape 3: \frac{7}{10}
   Shape 4: \frac{3}{5}
   Shape 5: \frac{1}{2}

3. In a class of 30 children, 14 are girls. What fraction are boys?
   \frac{16}{30} or \frac{8}{15}

4. Shade more triangles on this shape so that \frac{1}{3} is shaded.
   
   

   

   
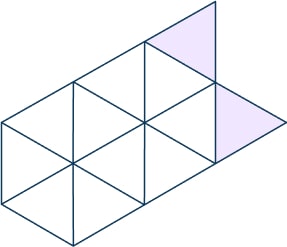
   Any two other triangles shaded, for example: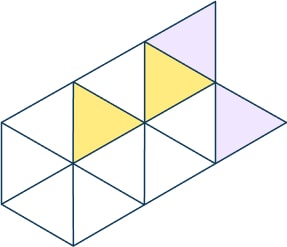
   
   

   

5. A bag contains red, green, and blue counters. Ahmed chooses 10 counters. \frac{3}{10} are red and 2 are green. What fraction are blue?
   \frac{5}{10} or \frac{1}{2}

Frequently asked questions