Teaching Percentages KS2: A Guide For Primary School Teachers From Year 3 To Year 6
Percentages in KS2 maths are part of a greater ‘connected’ set of topics, extending the knowledge of proportions pupils gain from working with fractions and decimals in earlier years.
This post will show you what that extension looks like in years 5 and 6, what your pupils should be able to do before moving on, and finally offer some practical suggestions as to how some objectives could be taught in the classroom.
Note: It’s recommended you read this article on teaching fractions at KS2 first.
What are percentages?
A percentage is a proportion of a whole number, expressed as a value out of a hundred. For example, 4 is one tenth of 40, or 10%. Percentages incorporate aspects of many other maths topics such as place value, fractions, especially equivalent fractions and decimal numbers.
They are typically encountered late in Key Stage 2 – Year 5 – alongside other more complex topics such as algebra and volume.
Percentages KS1
Though percentages are only explicitly mentioned in the curriculum from Year 5 onwards, much of the foundation of this unit begins in KS1 when students look at simple fractions.
Students may not know it yet, but all the work they have done with fractions can transfer to when they learn percentages in Year 5.
Percentages KS2
Percentages as a way of expressing proportion
Within the notes and guidance of the Year 5 curriculum is a crucial statement that, if missed by the teacher, can hinder this transferability and application of knowledge of fractions to percentages:
‘Pupils should be taught throughout that percentages, decimals and fractions are different ways of expressing proportions.’
From personal experience, it is when this link is not explicitly made that students see percentages as something ‘different’ rather than as merely another way of expressing proportions.
A consistent link in the models and manipulatives that students used when initially learning about fractions to their learning of percentages plays a crucial role in illuminating the link between the two mathematical concepts, and might be a good maths CPD topic.
What does percentage mean?
Percentage means ‘out of one hundred’.
When teaching a new concept, particularly one with unfamiliar vocabulary, I have always found it easier to start the unit by breaking down the word into something far more familiar to them.
When looking at the morphology of ‘percent’, we can see that it is made from two morphemes, ‘per’ and ‘cent’ and it is here we can draw on students’ prior knowledge in order to make connections to the new learning. They will already be familiar with other words that contain the morpheme ‘cent’ such as century (100 years), centimetre (one hundredth of a metre) and centipede (insect with supposedly 100 legs, though this is not true).
Here, we can draw out that the commonality between the words is ‘100’. So, when students are told that the morpheme ‘per’ means out of and cent means ‘one hundred’, they are able to see that percent means ‘out of 100.’ This is a form of proportion.
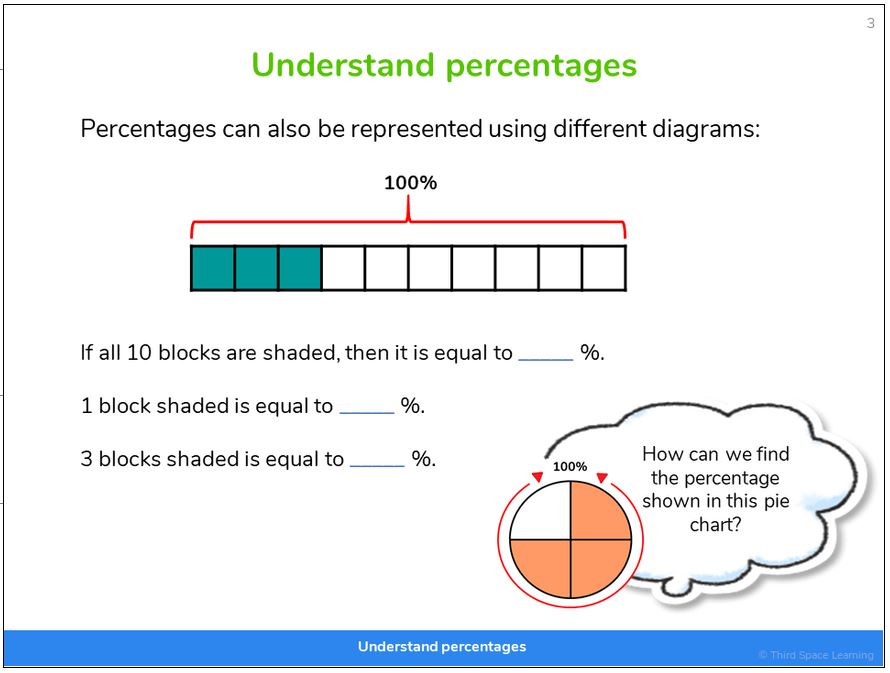
in this slide from Third Space Learning’s online interventions
The models and mathematical imagery that we use when teaching percentages should mirror those that we use for fractions.
Because students should have looked at the relationship between fractions and decimals before percentages, they should already have some mental models with which they can apply already to this unit of work.
Fractions, Decimals and Percentages Diagnostic Quiz
Work out which parts of percentages and its related topics your pupils have gaps in with this free diagnostic quiz.
Download Free Now!Percentages Year 5
In the National Curriculum for maths in England, for each area of maths outlined, there is both a statutory requirement and a non-statutory requirement. The statutory requirements in KS2 maths are as follows:
Year 5 pupils should be taught to:
- Recognise the per cent symbol (%) and understand that per cent relates to ‘number of parts per hundred’, and write percentages as a fraction with denominator 100, and as a decimal
- Solve problems which require knowing percentage and decimal equivalents of 1/2 , 1/4 , 1/5, 2/5 and 4/5 and those fractions with a denominator of a multiple of 10 or 25.
* The statements regarding percentages come from the fractions section of the National Curriculum. All statements that do not specifically mention percentages have been removed.
Non-statutory notes and guidance:
- Pupils should be taught throughout that percentages, decimals and fractions are different ways of expressing proportions.
- Pupils should make connections between percentages, fractions and decimals (for example, 100% represents a whole quantity and 1% is 1/100, 50% is 50/100, 25% is 25/100) and relate this to finding ‘fractions of’.
Percentages activities Year 5
For this lesson, I will look at the objective ‘solve problems which require knowing percentage and decimal equivalents of 1/2 , 1/4 , 1/5, 2/5 and 4/5 and those fractions with a denominator of a multiple of 10 or 25.’
It is here that it worth remembering that these are outcomes and not lesson objectives themselves. It is therefore desirable to break this objective down into smaller steps.
I will therefore look at how I would get students to recognise decimal and percentage equivalents as this is required before students can then solve problem with this knowledge.
When introducing percentages, I would first explain the morphology of the word as per the previous section. Next, I would draw out the relationship between percentages and fractions using the exact models as were used in a previous blog that looked at fractions.
This is not because of any inherit laziness on my part for coming up with some wonderous ideas of teaching percentages but rather because it draws on what the students know already and will make the work as accessible to everyone.
Before this, I ensure that students understand that when we talk about having 100%, what we mean is having one-whole. This would be demonstrated through showing complete or incomplete pictures of objects projected onto an interactive whiteboard where students would have to identify if 100% of the object is being shown.
After that, I would draw out the similarities between percentages and fractions using the same models that the students would have encountered when using Cuisenaire rods to learn about fractions.
Explain to students that purple rod is equal to 100% or one-whole.

You could ask students to find half the purple rod.
They will quickly identify that the red rod is half of the purple rod and place it as below, underneath the purple. They will do this even quicker than when they were asked to do it when covering fractions.
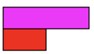
Here we can get students to think about the relationship between the red and the purple rod in terms of percentages. It will not take students long to realise that the red rod would represent 50% of the purple rod.
Ask them to find the other half of purple. Without difficulty students will be able to find another red rod and place it down. Here students will be able to see the two lots of 50% make 100%. At this point students will begin recognising the connection between two 1/2 making one-whole.
Ask them to find half of the red rod. By now they should be able to do this with ease.
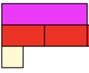
You can then use targeted questioning to ensure that students recognise that the white rod represents 1/4 of the purple rod – which represents 25%. You could then add additional white cubes to the train highlighting its value as a percentage and a fraction of the original purple rod.
This process would then be repeated with a yellow rod representing 100% so that students could look at the relationship with 5ths which they would have learnt in Year 5 when studying fractions.
I would also show how 5ths can be represented when an orange rod is used to represent 100%.
This is so students can think about what is the same and what is different about the two models
Percentages word problems Year 5
A typical word problem for Year 5 would be to apply their new learning into a meaningful and realistic context. For example:
There are 180 children in a school. 30% have milk every day. How many children do not have milk?
Here students would be required to draw on their understanding of bar models and, to a certain extent, their ability to properly comprehend the problem as it is the remaining 70% that must be given as the answer, not the 30% that the students may calculate first.
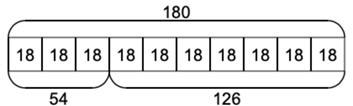
Answer: 126 pupils do not have milk every day.
Percentages: reasoning and problem solving Year 5
A typical reasoning question that students would be expected to solve would be the following:
Chris says that 75% is equal to 7.5
Lloyd says that 75% is equal to 0.75.
Explain who is correct.
This question assesses students’ understanding of converting between percentages and decimals, particularly if students are trying to use tricks or shortcuts to answer the question or simply rushing through.
Lloyd is correct and to show this students may draw diagrams showing that 75% is equal to 0.75 or explain that as 100% is in relation to a whole, which would be 1.0 and 7.5 is greater than 1, the answer must be 0.75.
Percentages Year 6
- Recall and use equivalences between simple fractions, decimals and percentages, including in different contexts.
- Solve problems involving the calculation of percentages [for example, of measures, and such as 15% of 360] and the use of percentages for comparison
Non-statutory notes and guidance:
- Pupils link percentages or 360° to calculating angles of pie charts.
Percentages activities Year 6
This lesson idea will focus on looking at the objective ‘Solve problems involving the calculation of percentages [for example, of measures, and such as 15% of 360] and the use of percentages for comparison.’
Again, this objective is an outcome, therefore it is highly probable that in order for students to be successful it is necessary to break this objective down even further. As such, this lesson idea will look at finding percentages of amounts.
As echoed through this post, while the context of the problems may be new to the students, the underlying mathematics and arithmetic needed for students to succeed should be well within a students’ grasp.
Prior to this lesson, I would have taught the other objective from Year 6 so students will be familiar with equivalent percentages, fractions and decimals. The reason for this is that if students know these equivalences off by heart, then they can relate this back to when they learnt fractions of amounts. Thus, 25% of 200 becomes 1/4 of 200.
Students should know that to find 1/4 we share something into 4 equal groups and by Year 6, I would expect most of the students to know that this is 50. The bar can thus be completed as the following:
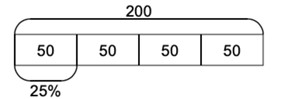
Students can then see that 25% is equal to 50.
For the first lesson of percentages of amount, I would guide students through finding 1%, 10%, 25%, 50% and 75%. I would make sure that I taught 25%, 50% and 75% first as this will prevent students developing the misconception that you divide the whole by the number in the percentage to find the percentage as is the case when you try to find 10%.
As students have seen already that this is not the case for 25%, 50% and 75%, this misconception would be unlikely to develop. Below are the bar models that I would use to demonstrate each percentage. When teaching, I will always be making the link to their understanding of fractions and decimals to link this learning with prior learning.
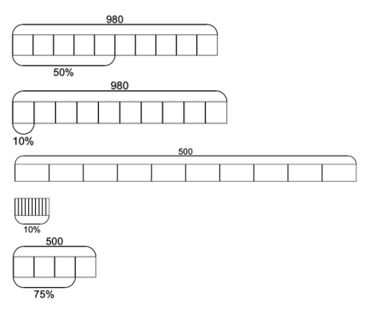
Once students are confident with finding these percentages of amounts, then we can look at partitioning the percentage of amounts into manageable chunks for numbers where the percentage has a value greater than zero in the ones, e.g. 35% which is demonstrated below.

Here, students can partition 35 into three groups of 10 and one group of 5 before calculating the percentage value for each part and adding the totals together.
At the initial stage of this, I get students to add both the percentage value and the value of the whole so that they can see the percentage equalling 35%.
Percentages word problems Year 6
A typical problem that students would be expected to solve would be the following:
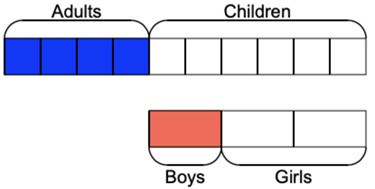
At a restaurant 4/10 of the diners were adults. The rest of the diners were children. Of the children, there were half as many boys than there were girls. Give the percentage of boys and girls at the restaurant.
Here, using the bar model would be appropriate to show the mathematics.
Students should be familiar enough with bar models to draw the above. Where they may struggle is with the part that says, ‘there were half as many boys than there were girls.’
A common misconception to arise here is that students will simply halve the parts in the model that make up the children and get the answer that 30% of the diners are girls and 30% of the diners are girls.
This is of course not true. To counter this misconception, it is best to ‘bring down’ the section of the bar that is related to only the children.
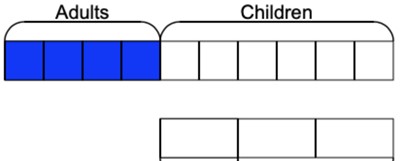
Model this to the students. The use of a dotted arrow indicates that the bars are one of the same and not a comparison of each other. Note how they are of the same length but purposefully only containing three parts with each part being equal to two parts of the bar above it.
This is to help bring out the mathematics of the ‘half as many boys as girls’ part of the question. I would be explicit in that this section is still representative of 60% of all diners.
Here we can see that each part in the bottom bar is worth 20% and so we can use this to help us solve the rest of the problem. We are therefore looking for a way to partition 60 in such a way that one part is half of the other part.
As we know that each part is worth 20% students should be able to see that the remaining two parts are equal to 40%. As 20 is half of 40, this fulfils the criteria. When we add this to the mode, we end up with the following:
Percentages: reasoning and problem solving Year 6
Once a method has been taught to students, they very often over rely on the use of that method to the detriment of other mathematical thinking. For example, it is not too uncommon in the classroom, when students are asked to work out 90% of a number, they will often fall back into dividing the whole by 10 and then proceed to multiply that result by 9.
Of course, this is a perfectly legitimate way of solving such a problem, but is this the most efficient and mathematical way to solve such a problem? I think not.
Having found what 10% of the whole was, all the students then had to do was take the value of 10% from the whole away from the whole to find 90%. This is where open tasks such as the ones below are helpful for students as it provides them with the space and freedom to think mathematically.
How many ways can you find 60% of 300?
Here there are a myriad of ways for students to get thinking of all the different ways that they can think of to make 60%. As ever, it is the rich conversations that you have with pupils during and after such activities that can illuminate and deepen there mathematical thinking.
Percentage is a complex topic, but one closely aligned with previous learning. Hopefully this post has given you some good ideas to help your pupils approach it with confidence, no matter which KS2 year they are in!
DO YOU HAVE PUPILS WHO NEED MORE SUPPORT IN MATHS?
Every week Third Space Learning’s specialist primary maths tutors support thousands of students across hundreds of schools with weekly online 1 to 1 maths lessons designed to plug gaps and boost progress.
Since 2013 these personalised one to one lessons have helped over 150,000 primary and secondary students become more confident, able mathematicians.
Learn about the scaffolded lesson content or request a personalised quote for your school to speak to us about your school’s needs and how we can help.