How To Add Fractions: Step By Step Guide For Primary School Teachers & Pupils

Children are introduced to fractions from KS1, but won’t be taught about how to add fractions until KS2. This can be quite a complex procedure, especially with fractions that have different denominators.

Here you’ll find our step-by-step guide on how to add fractions, with worked examples and practice problems to use with your pupils. This will help you to break down the process of teaching KS2 fractions, and apply this to other topics that involve comparing fractions, decimals, and percentages.

How to add fractions: what does it mean?

Just like adding integers, adding fractions means finding the total, or sum, of two or more fractions. 

When do pupils learn about how to add fractions?

Pupils aren’t expected to learn the process of fraction addition until Key Stage 2. In Years 3 and 4, children learn to add fractions with the same denominator. In Years 5 and 6, children learn to add fractions with different denominators.

The National Curriculum states that pupils should be taught to:

• Year 3: learn how to add and how to subtract fractions with the same denominator within one whole [for example, \frac{5}{7} + \frac{1}{7} = \frac{6}{7} ].
• Year 4: add and subtract fractions with the same denominator.
• Year 5: add and subtract fractions with the same denominator and denominators that are multiples of the same number.
• Year 6: add and subtract fractions with different denominators and mixed numbers, looking at the type of fraction: equivalent fractions.

How to add fractions: step by step guide

To introduce children to adding fractions in lower Key Stage 2, children are first taught to add fractions with the same denominator, or ‘like denominators’. This is because they need only calculate with the numerators (when the denominators are the same, the fraction sizes are the same). 

How to add fractions with the same denominator

When the denominators of two fractions are the same, we can add and subtract these from each other as parts of a whole.

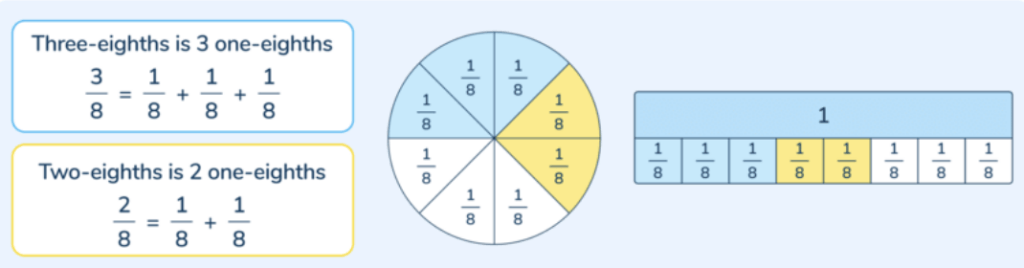
Using these diagrams, we can see that:

• \frac{3}{8} + \frac{2}{8} = \frac{5}{8}

• \frac{2}{8} + \frac{3}{8} = \frac{5}{8}

• \frac{5}{8} - \frac{2}{8} = \frac{3}{8}

• \frac{5}{8} + \frac{3}{8} = \frac{2}{8}

It may be helpful to write these number sentences on the board with the denominators as words and the numerators as digits, to avoid the misconception that the denominators need adding as well (for example, “3 eighths + 2 eighths = 5 eighths”, etc.)

How to add fractions with different denominators

In Upper Key Stage 2, children are taught to add fractions with different denominators, or ‘unlike denominators’. Fractions with different denominators are often called unlike fractions.

This is firstly taught using fractions with related denominators (where both denominators are multiples of the same number), then later in Year 6 with unrelated denominators.

When adding or subtracting fractions, the denominators need to be the same. Let’s look at a pair of fractions where one denominator is a multiple of another. Using diagrams, we can add the fractions:

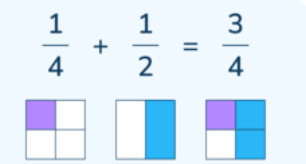
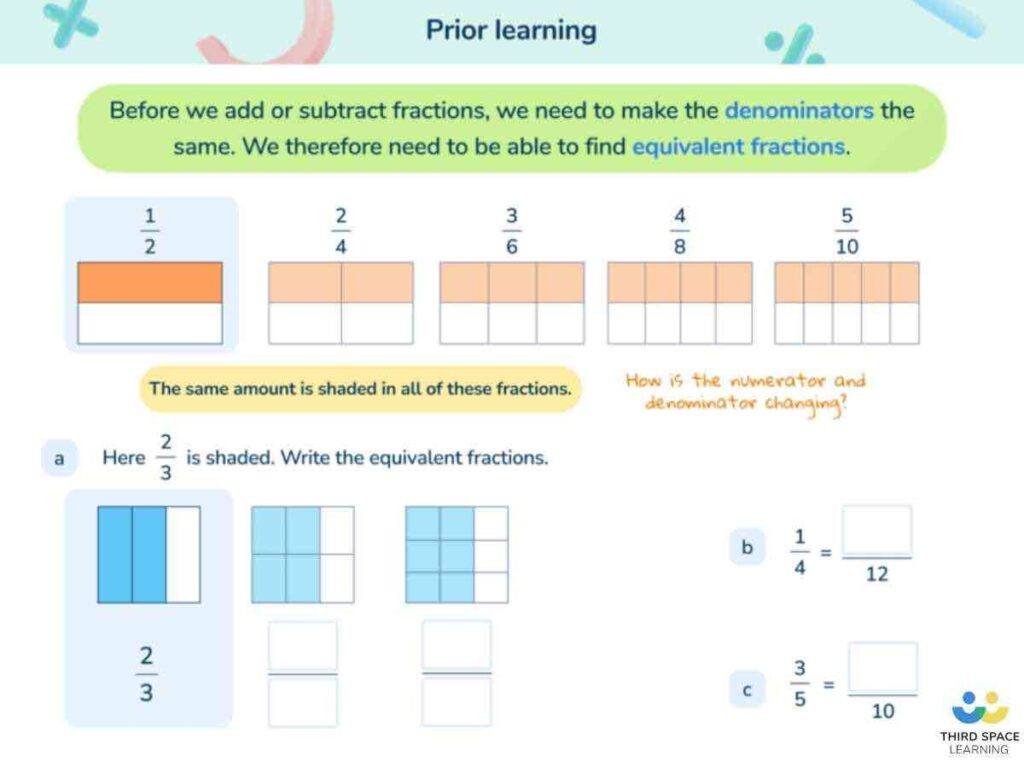
Without diagrams, we can add them by finding a common denominator (a common denominator is when two or more fractions have the same denominator).

To find a common denominator, we need to find the Lowest Common Multiple (LCM) of the denominators (any common multiple will work, but the LCM is more efficient). We should then find equivalent fractions with this new denominator.

\frac{1}{2} is equivalent to \frac{2}{4} , so we can now add the numerators: \frac{1}{4} + \frac{2}{4} = \frac{3}{4}

This is an example of adding related fractions because 4 and 2 are multiples of the same number. To add unrelated fractions, the method is the same.

Let’s try \frac{1}{3} + \frac{2}{5} using the same steps as above:

Step 1: Find a common denominator: the LCM of 3 and 5 is 15

Step 2: Find equivalent fractions using the new denominator: \frac{1}{3} = \frac{5}{15} and \frac{2}{5} = \frac{6}{15}

Step 3: Add the numerators: \frac{5}{15} + \frac{6}{15} = \frac{11}{15}

How to add fractions with whole numbers

In Year 6, children are taught to add mixed numbers (sometimes known as mixed fractions). This can be done by partitioning the mixed numbers into whole numbers and fractions, adding the fractions by following the same method as above, and then recombining the parts. For example, with 1\frac{1}{2} + 1\frac{1}{3} :

1. Partition the mixed numbers: 1 + \frac{1}{2} + 1 + \frac{1}{3}

2. Find a common denominator for the fractions: the LCM of 2 and 3 is 6

3. Find equivalent fractions using the new denominator: \frac{1}{2} = \frac{3}{6} and \frac{1}{3} = \frac{2}{6}

4. Add the numerators: \frac{3}{6} + \frac{2}{6} = \frac{5}{6}

5. Recombine the parts: 1 + 1 + \frac{5}{6} = 2\frac{5}{6}

Sometimes, the fractions might equal an improper fraction when added. In this case, convert it to a mixed number and add it together with the whole number parts. 

For example, 1\frac{1}{2} + 1\frac{2}{3} = 1 + \frac{1}{2} + 1 + \frac{2}{3} = 1 + 1 + \frac{3}{6} + \frac{4}{6} = 2 + \frac{7}{6} = 2 + 1\frac{1}{6} = 3\frac{1}{6} .

How to add fractions: worked examples

1. \frac{3}{4} + \frac{7}{12} =
    
   1. Find a common denominator: the LCM of 4 and 12 is 12 (some people may choose a larger denominator, such as 24 or 48 - this will still give you the correct answer but you will need to know how to simplify fractions so you can simplify this at the end)
    2. Find equivalent fractions using the new denominator: \frac{3}{4} = \frac{9}{12} and the second fraction is already in twelfths
     3. Add the numerators: \frac{9}{12} + \frac{7}{12} = \frac{16}{12} (as an improper fraction) or \frac{14}{12} (as a mixed number) or 1\frac{1}{3} (simplified)

2. Circle two cards that give a total of 5.
   
   

   

   
   
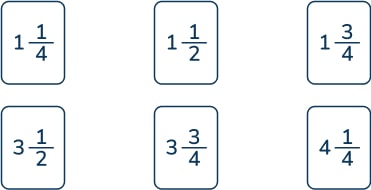
   We can rule out 4\frac{1}{4} (bottom right) as it would require a proper fraction to equal 5, and all these options are mixed numbers. This leaves both of the mixed number cards beginning with 3 (bottom left and middle) to match with a mixed number card beginning with 1 (any on the top row). There are two possible pairs for the answer: 3\frac{1}{2} + 1\frac{1}{2} , and 3\frac{3}{4} + 1\frac{1}{4} . A misconception might be that 1\frac{3}{4} + 4\frac{1}{4} = 5 because 1 + 4 = 5 and \frac{3}{4} + \frac{1}{4} are a number bond to 1.

3. A head teacher orders pizza for her staff. The lower school teachers eat 1\frac{2}{3} pizzas between them. The upper school teachers eat 2\frac{1}{5} pizzas between them. How many pizzas have been eaten altogether?
       
   1. Partition the mixed numbers: 1 + \frac{2}{3} + 2 + \frac{1}{5}
   2. Find a common denominator for the fractions: the LCM of 3 and 5 is 15
   3. Find equivalent fractions using the new denominator: \frac{2}{3} = \frac{10}{15} and \frac{1}{5} = \frac{3}{15}
   4. Add the numerators: \frac{10}{15} + \frac{3}{15} = \frac{13}{15}
   5. Recombine the parts: 1 + 2 + \frac{13}{15} , so the final answer is 3\frac{13}{15} pizzas

How to add fractions: practice questions

1. 2\frac{1}{6} + 3\frac{2}{5} = ?
   
   Answer: 5\frac{17}{30}

2. Use three of these fraction cards to complete the sum below.
   
   

   

   
   
   

   

   
   
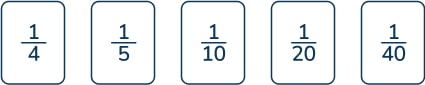
   Answer: {1}{4} + \frac{1}{5} + \frac{1}{20}

3. \frac{1}{3} + \frac{1}{4} + \frac{1}{6} = ?
   
   Answer: \frac{9}{12} or \frac{3}{4}

4. Some children are using ribbon for a DT project. One child cuts off \frac{2}{5} of the ribbon. Another cuts off 1/7 of the ribbon. How much of the ribbon do they have altogether?
   
   Answer: \frac{19}{35}

5. \frac{13}{12} + \frac{7}{6} = ?
   
   Answer: \frac{27}{12} or 2 \frac{3}{12} or 2 \frac{1}{4}

Further reading:

• How To Divide Fractions: Step By Step Guide
• 10 Fun Simple Fraction Games For KS1 And KS2
• What Is A Unit Fraction: Explained For Primary School
• How To Teach Fractions Key Stage 2: Maths Bootcamp

Frequently asked questions

Do you have pupils who need extra support in maths?
Every week Third Space Learning's maths specialist tutors support thousands of pupils across hundreds of schools with weekly online 1-to-1 lessons and maths interventions designed to plug gaps and boost progress.

Since 2013 we've helped over 150,000 primary and secondary school pupils become more confident, able mathematicians. Learn more or request a personalised quote for your school to speak to us about your school's needs and how we can help.