24 Fraction Questions And Answers To Test Fractions Knowledge And Skills From KS2 to GCSE
In this blog, we take a look at the sorts of skills pupils need to tackle fraction questions and fraction word problems, and then provide examples of the different sorts of fraction questions children are likely to encounter in KS2, KS3, and KS4.
Fractions key skills
Some of the key fractions skills that pupils will learn are:
- How to find a fraction of an amount
- How to add fractions and how to subtract fractions
- Fraction, decimal, and percentage conversions
Below we will touch on each of these skills and provide links to more detail and examples.
Fractions Intervention Pack
Try these lessons to help your pupils develop their knowledge and understanding of fractions.
Download Free Now!
How to find a fraction of an amount
To find a fraction of a value, we need to know how to multiply fractions and how to divide fractions. The process involves dividing the value by the denominator and then multiplying that answer by the numerator.
For example, find \cfrac{2}{5} \, of 30
First, we find \cfrac{1}{5} \, of 30, by dividing 30 by 5.
\cfrac{1}{5} \, of 30 = 30 \div 5 = 6
Next, we find \cfrac{2}{5} \, of 30 by multiplying the asnwer by 2.
\cfrac{2}{5} \, of 30 = 6 \times 2 = 12
Unlimited maths tutoring for primary schools with Skye, our AI tutor
Built on the same principles, pedagogy and curriculum as our traditional tutoring but with more flexibility, reach and lower cost.
Join the schools already helping hundreds of primary pupils nationwide with Skye’s one to one maths tutoring
Find out moreHow to add or subtract fractions with different denominators
To add and subtract fractions with different denominators, we need to rewrite the fractions with a common denominator. To do this, we look for the lowest common multiple (lcm) of the denominators.
Let’s look at an example: \cfrac{2}{5} + \cfrac{1}{4}
The lcm of 5 and 4 is 20, so we rewrite the fractions, using our knowledge of equivalent fractions, with a denominator of 20.
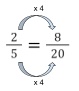
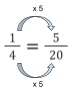
We can rewrite the first fraction as \cfrac{8}{20} \, and the second fraction as \cfrac{5}{20} \, .
Therefore \cfrac{2}{5} + \cfrac{1}{4}=\cfrac{8}{20}+\cfrac{5}{20}
Once we have the two fractions written with the same denominator, we can add the numerators. The denominator remains the same.
\cfrac{8}{20}+\cfrac{5}{20}=\cfrac{13}{20}
How to compare and convert fractions, decimals and percentages
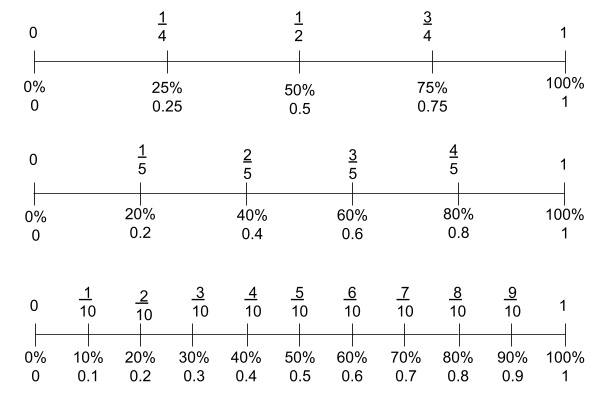
Fractions are one way of measuring parts of a whole. Percentages and decimals are other ways of measuring parts of a whole. Pupils will first learn about key equivalences between the most common fractions, decimals and percentages, such as halves, quarters, and tenths. Later, in KS3, they will then learn methods for converting between any fractions, decimals, and percentages.
Here are some helpful visuals for the most common fractions, decimals, and percentages:
Fraction questions
There are a variety of fraction questions that might be asked in KS2, KS3, and KS4. Here we focus on fraction word problems and problem-solving questions which often provide the greatest challenge to pupils at primary school and secondary school.
At KS2, using real-world problems together with concrete resources or maths manipulatives is one of the best ways to help pupils visualise and understand what they are being asked to do.
In KS3 and KS4, word problems and problem solving questions can encourage students to think more deeply about about the processes and steps involved in a question.
Fractions in KS2
At the beginning of KS2, pupils will have an understanding of basic fractions, such as \cfrac{1}{2}, \cfrac{1}{4}, and \cfrac{3}{4}.
They will be able to write a fraction and find a fraction of a shape or a quantity. Over the course of KS2, they will spend a significant amount of time developing their knowledge of fractions. By the end of KS2, pupils will have covered:
- Finding a fraction of a quantity
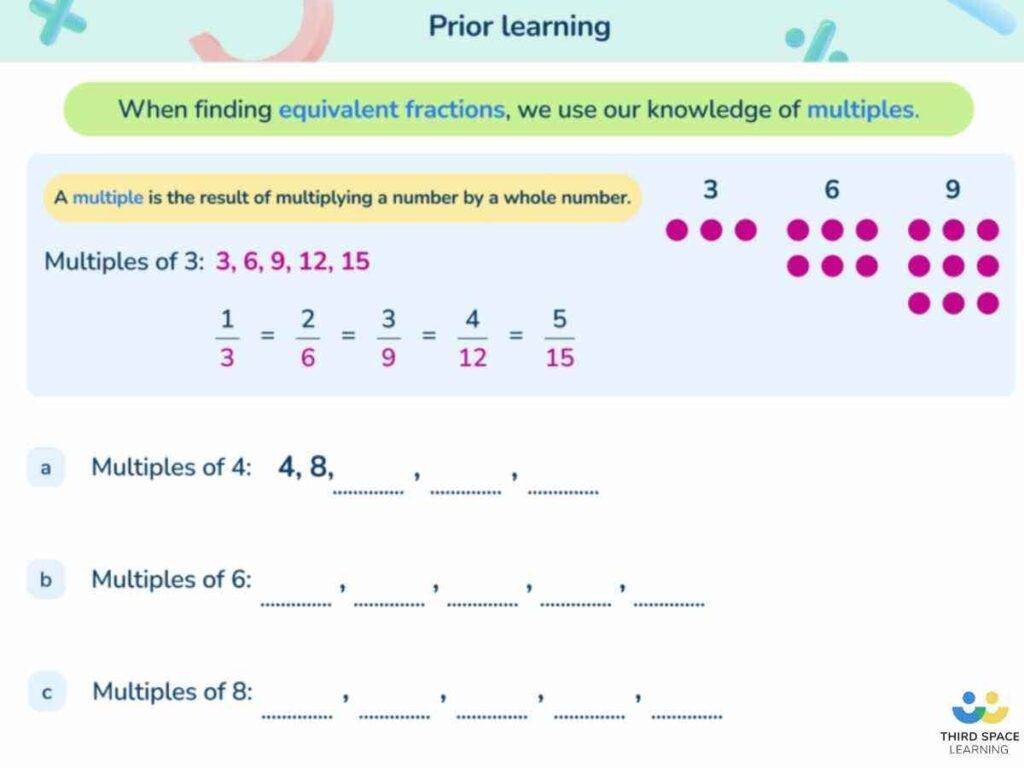
- Equivalent fractions
- Ordering and comparing fractions
- Adding and subtracting fractions with the same denominator
- Adding and subtracting fractions with different denominators
- Multiplying fractions and dividing fractions by whole numbers and fractions
- Improper fractions and mixed numbers (sometimes called mixed fractions)
- Equivalences between fractions, decimal and percentages
Find out more: KS2 fractions: a teacher’s guide
Read more:
- What Is A Unit Fraction: Explained For Primary School
- What Is An Improper Fraction: Explained For Primary School
- Fractions for Kids: A Comprehensive Guide
- How To Teach Fractions Key Stage 2: Maths Bootcamp
- Fraction games for KS1 and KS2
Lower KS2 fraction questions
1. Natalie had 20 sweets. She ate \cfrac{1}{4} \, of them.
How many sweets did Natalie eat?
\cfrac{1}{4} \, of 20 = 20 \div 4 = 5
2. Osian had some money. He gave \cfrac{1}{5} of the money to Ethan. He gave \cfrac{2}{5} of the money to Ffion. What fraction of the money did he give away in total?
He gave away \cfrac{1}{5}+\cfrac{2}{5}=\cfrac{3}{5}
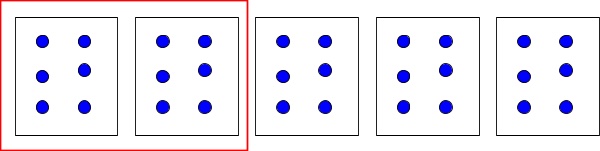
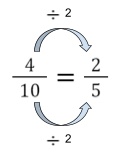
3. Choose the correct fraction to go in the box:
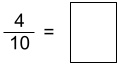
Upper KS2 fraction questions
4. There are 32 pupils in a class. \cfrac{3}{8} \, of the pupils are girls.
How many of the pupils are boys?
\cfrac{1}{8} \, of 32 = 32 \div 8 = 4
\cfrac{3}{8} \, of 32 = 4 \times 3=12, so there are 12 girls.
32-12=20, so there are 20 boys.
5. Which fraction is the odd one out?
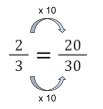
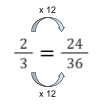
\cfrac{12}{13} \, is not equivalent to \cfrac{2}{3} \, so it is the odd one out.
6. Ben and Jacob both received the same amount of pocket money.
Ben spent \cfrac{3}{4} \, of his pocket money. Jacob spent \cfrac{13}{20} \, of his pocket money.
Choose the correct symbol to make this sentence correct.
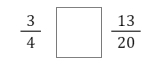
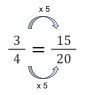
Therefore \cfrac{3}{4} > \cfrac{13}{20}
7. In a jug, there is \cfrac{2}{3} \, litre of juice.
Willow pours \cfrac{1}{5} \, litre of juice from the jug. What fraction of a litre is left in the jug?
\cfrac{2}{3}-\cfrac{1}{5} = \cfrac{10}{15}-\cfrac{3}{15} =\cfrac{7}{15}
8. Tim walked \cfrac{3}{7} \, of a mile each day, for 5 days.
How far did Tim walk in total?
5 \times \cfrac{3}{7} = \cfrac{15}{7} = 2 \cfrac{1}{7}
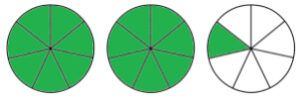
9. April got 12 questions wrong on a test.
This was \cfrac{2}{5} \, of the questions.
How many questions were on the test?
\begin{aligned} \cfrac{2}{5}&=12\\\\ \cfrac{1}{5}&=12 \div 2 = 6\\\\ \cfrac{5}{5}&=6 \times 5 = 30 \end{aligned}
Looking for more KS2 fraction questions?
These fraction worksheets provide lots more fraction questions, covering both basic elements and more complex problems. Answers are also included:
- Year 1 ready to go lessons and worksheets
- Year 2 tarsia find half worksheet
- Year 3 add fractions worksheet
- Year 4 extension questions fractions worksheet
- Year 5 subtract fractions worksheet
- Year 6 Ordering Fractions, Decimals and Percentages Worksheet
Fractions in KS3
In KS3, pupils develop their confidence in working with fractions. They practise all of the skills learnt at KS2 and learn to apply these to a variety of problems. Fractions will be learnt about as a topic in their own right, but will also be increasingly embedded into other areas of maths, such as algebra and geometry, as pupils progress through KS3.
Manipulating fractions questions
10. The ratio of men:women working in a company is 3:5. What fraction of the workers are men?
For every 3 men, there are 5 women. Therefore in a total of 8 people, there are 3 men. The fraction of the workers who are men is \cfrac{3}{8} \, .
11. Ellie says that \cfrac{14}{6}=2\cfrac{1}{3} \, .
Is Ellie correct?
Explain how you know.
Yes
No
We can’t tell
2 \cfrac{1}{3} \,= \cfrac{2 \times 3 +1}{3} \, = \cfrac{7}{3}
\cfrac{7}{3} = \cfrac{14}{6}
Finding a fraction of an amount questions
12. 2400 people attended a concert. \cfrac{3}{8} \, of the people were men.
\cfrac{5}{12} \, of the people were women. The rest of the people were children.
How many children were at the concert?
\cfrac{3}{8} \, of 2400
2400 \div 8 =300
300 \times 3=900
\cfrac{5}{12} \, of 2400
2400 \div 12 =200
200 \times 5=1000
2400-900-1000=500
13. In January the value of a house was £280000.
By August, the value of the house had decreased by \cfrac{1}{10} \, .
Find the value of the house in August.
\cfrac{1}{10} \, of 280000
280000 \div 10=28000
280000-28000=252000
Calculating with fractions and mixed numbers questions
14. Richard wants to calculate \cfrac{5}{8} \div \cfrac{4}{5} \, . Select the correct method.
15. Here is a signpost.
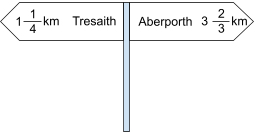
What is the distance from Tresaith to Aberporth?
\begin{aligned} 1\cfrac{1}{4} + 3\cfrac{2}{3} &= \cfrac{5}{4}+\cfrac{11}{3}\\\\ &= \cfrac{15}{12} +\frac{44}{12}\\\\ &=\cfrac{59}{12}\\\\ &=4\cfrac{11}{12} \end{aligned}
Fractions, decimals and percentages questions
16. Frank scored 32 out of 40 in a test. What percentage of the questions did Frank answer correctly?
\cfrac{32}{40}=\cfrac{8}{10}=80\%
17. Write 2.35 as an improper fraction.
Give your answer in its simplest form.
2.35= \cfrac{235}{100}
Simplifying \cfrac{235}{100} gives us \cfrac{47}{20}
Ensure you follow the instructions carefully and give your answer as an improper
fraction in its simplest form.
Fractions in KS4 and for GCSE
In KS4, students continue to develop their fluency in using fractions to solve problems and will be required to apply their knowledge of fractions within many different maths topics. GCSE maths papers, from all exam boards (including AQA, Edexcel and OCR) will, almost certainly, contain questions involving fractions.
These may appear as standard procedural questions, such as calculate 2\cfrac{1}{4} \times 3\cfrac{2}{3} \,. It is also likely that there will be questions from other areas of maths, such as algebra, geometry, and probability, which involve fractions.
Take a look at our GCSE maths guides on fractions:
- Adding and subtracting fractions
- Dividing fractions
- Fractions of amounts
- Fractions, decimals, and percentages
- Improper fraction to mixed number
GCSE fraction questions (Foundation)
18. Write these fractions in order of size, starting with the smallest.
\cfrac{2}{5} \hspace{.5cm} \cfrac{3}{8} \hspace{.5cm} \cfrac{3}{10} \hspace{.5cm} \cfrac{9}{20}
\cfrac{2}{5} \, =\cfrac{16}{40}
\cfrac{3}{8} \, =\cfrac{15}{40}
\cfrac{3}{10} \, =\cfrac{12}{40}
\cfrac{9}{20} \, =\cfrac{18}{40}
\cfrac{12}{40}, \, \cfrac{15}{40} , \, \cfrac{16}{40}, \, \cfrac{18}{40}
\cfrac{3}{10}, \, \cfrac{3}{8} , \, \cfrac{2}{5}, \, \cfrac{9}{20}
19. Work out the perimeter of this rectangle. Give your answer as a mixed number in its simplest form.
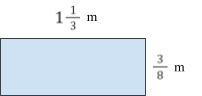
\begin{aligned} 1 \cfrac{1}{3} \, + 1 \cfrac{1}{3} \, + \cfrac{3}{8} \, + \cfrac{3}{8} &= \cfrac{4}{3} + \cfrac{4}{3} \, + \cfrac{3}{8} \, +\cfrac{3}{8}\\\\ &=\cfrac{32}{24} \, + \cfrac{32}{24} \, + \cfrac{9}{24} \, +\cfrac{9}{24}\\\\ &=\cfrac{82}{24}\\\\ &= \cfrac{41}{12}\\\\ &=3 \cfrac{5}{12} \end{aligned}
20. Here are the first three terms of a sequence:
\cfrac{2}{3}, \, \cfrac{4}{9}, \, \cfrac{8}{27}
The rule to find the next term in the sequence is multiply by \cfrac{2}{3} \, .
Find the 5th term in the sequence.
\cfrac{8}{27} \, \times \cfrac{2}{3} = \cfrac{16}{81}
\cfrac{16}{81} \, \times \cfrac{2}{3} = \cfrac{32}{243}
GCSE fraction questions (Higher)
21. On a farm, the ratio of white sheep:black sheep is 3 \, \text{:} \, 1.
\cfrac{2}{3} \, of the white sheep are ewes. \cfrac{2}{5} \, of the black sheep are ewes.
There are 144 ewes on the farm. How many sheep are there on the farm in total?
\cfrac{3}{4} \, of the sheep are white. \cfrac{2}{3} \, \times \cfrac{3}{4} \, = \cfrac{6}{12} \, of the sheep are white ewes.
\cfrac{1}{4} \, of the sheep are black. \cfrac{2}{5} \, \times \cfrac{1}{4} \, = \cfrac{2}{20} \, of the sheep are black ewes.
\cfrac{6}{12} \, +\cfrac{2}{20} \, =\cfrac{30}{60} \, +\cfrac{6}{60} \, =\cfrac{36}{60}
\cfrac{36}{60} \, of the sheep are ewes.
\cfrac{36}{60}=144
\cfrac{1}{60} \, =144 \div 36=4
\cfrac{60}{60} \, = 4 \times 60=240
22. Write \cfrac{3}{x-2}-\cfrac{5}{x+4} as a single fraction, in its simplest form.
\begin{aligned} \cfrac{3}{x-2}\,-\cfrac{5}{x+4} \, &=\cfrac{3(x+4)}{(x+4)(x-2)}\,-\cfrac{5(x-2)}{(x+4)(x-2)}\\\\ &=\cfrac{3x+12-(5x-10)}{(x+4)(x-2)}\\\\ &=\cfrac{-2x+2}{(x+4)(x-2)} \end{aligned}
23. Find the value of \cfrac{ab^{2}}{c} when a=-2, \, b=\cfrac{3}{8} \, and c=\cfrac{1}{4}.
Give your answer in its simplest form.
\begin{aligned} \cfrac{ab^{2}}{c} \, &=\cfrac{-2 \times (\cfrac{3}{8})^{2}}{\cfrac{1}{4}}\\\\ &=\cfrac{-2 \times \cfrac{9}{64}}{\cfrac{1}{4}}\\\\ &=\cfrac{-\cfrac{18}{64}}{\cfrac{1}{4}}\\\\ &=-\cfrac{18}{64} \, \times \cfrac{4}{1}\\\\ &=-\cfrac{72}{64}\\\\ &=-\cfrac{9}{8} \end{aligned}
24. Express 0.2\dot{8}\dot{1} as a fraction.
\begin{aligned} x&=0.281818181…\\\\ 10x&=2.81818181…\\\\ 1000x&=281.818181…\\\\ 990x&=279\\\\ x&=\cfrac{279}{990}\\\\ x&=\cfrac{31}{110} \end{aligned}
Looking for more KS3 and KS4 fraction questions?
These KS3 maths worksheets and GCSE maths worksheets provide lots more fraction questions with answers included:
- Subtracting Fractions Worksheet
- Fractions Decimals and Percentages Worksheet
- Equivalent Fractions Worksheet
- Fractions of Amounts Worksheet
- Mixed Numbers to Improper Fractions Worksheet
More GCSE fraction support
Third Space Learning’s free GCSE maths resource library contains detailed lessons with step-by-step instructions on how to solve fraction problems at secondary, as well as fraction worksheets with practice questions and more GCSE exam questions.
Fraction questions FAQs
A fraction of an amount at GCSE is when we are asked to find a certain fraction of an amount, for example \cfrac{3}{5} \, of 20.
To do this, we divide by the denominator and then multiply by the numerator.
20\div 5 = 4
4 \times 3 =12
So \cfrac{3}{5} of 20=12.
An example of a fraction is \cfrac{3}{10}. This is read as ‘three tenths’ and means thee out of every ten.
You may see different types of fractions:
Unit fractions have a numerator of 1, for example \cfrac{1}{8} \, .
Proper fractions have a numerator that is smaller than the denominator, for example \cfrac{3}{4} \, .
Improper fractions have a numerator that is greater than the denominator, for example \cfrac{5}{2} \, .
Mixed number fractions (mixed fractions) are made up of a whole number and a fraction, for example 2\cfrac{1}{3} \, .
When pupils learn how to simplify fractions we look for common factors of the numerator and the denominator. If there are common factors, we divide both the numerator and the denominator by the common factor to find an equivalent, simpler fraction. We continue doing this until there are no more common factors.
For example, simplify \cfrac{20}{40} \, .
10 is a common factor of 20 and 40. Dividing both 20 and 40 by 10 gives us \cfrac{2}{4} \, .
2 is a common factor of 2 and 4. Dividing both 2 and 4 by 2 gives us \cfrac{1}{2} \, .
There are no more common factors of 1 and 2, so we cannot simplify any further.
DO YOU HAVE PUPILS WHO NEED MORE SUPPORT IN MATHS?
Every week Third Space Learning’s specialist primary maths tutors support thousands of students across hundreds of schools with weekly online 1 to 1 maths lessons designed to plug gaps and boost progress.
Since 2013 these personalised one to one lessons have helped over 169,000 primary and secondary students become more confident, able mathematicians.
Learn about the scaffolded lesson content or request a personalised quote for your school to speak to us about your school’s needs and how we can help.
