How To Divide Fractions: Step By Step Guide For Primary School Teachers & Pupils

October 23, 2023 | 6 min read

Sophie Bartlett

Once pupils have learnt about multiplying, adding, and subtracting fractions, they are taught about how to divide fractions. This isn’t covered until year 6 as it is one of the most complex things pupils are required to do with fractions in primary school.

In this article, we’ll show you a step-by-step process on how to divide fractions, using visual diagrams to help you break down this topic for you and your pupils. Below you will also find practice fraction questions and worked examples with answers.

How to divide fractions: step by step

Dividing fractions by integers

When fractions are divided by integers (whole numbers), they become smaller. We can divide a fraction by a whole number using an equivalent multiplication calculation once pupils know how to multiply fractions. For example, multiplying by $\frac{1}{2}$ and dividing by 2 give the same result.

Download Fractions Intervention Pack

Download these fraction intervention questions to help your students feel confident on fractions.

Download Free Now!

Let’s look at $\frac{1}{2} ÷ 2$ .

$\frac{1}{4}$ of the rectangle is shaded.

Let’s divide each quarter into 2 equal parts. We now have 8 equal parts with only 1 shaded (half of the original quarter), so the final answer is $\frac{1}{8}$ .

$\frac{1}{4} ÷ 2$ is the same as $\frac{1}{2}$ of $\frac{1}{4}$ , or $\frac{1}{2} × \frac{1}{4}$ (because ‘of’ can mean multiply).

Let’s try $\frac{2}{5} ÷ 3$ .

Shade $\frac{2}{5}$ of the rectangle.

Divide each fifth into 3 equal parts. $\frac{2}{5} ÷ 3$ is the same as finding $\frac{1}{3}$ of $\frac{2}{5}$ .

how to divide fractions in 3 equal parts

Two parts out of 15 are shaded in dark green, so the answer is $\frac{2}{15}$ .

$\frac{2}{5} ÷ 3$ , or $\frac{1}{3}$ of $\frac{2}{5}$ , is the same as $\frac{1}{3} × \frac{2}{5}$ . To multiply fractions, we multiply the numerators and the denominators together. $\frac{1}{3} × \frac{2}{5} = \frac{2}{15}$ .

In essence, to divide by an integer, you can multiply by its reciprocal (the reciprocal being the number divided by 1). For example, dividing by 2 is the same as multiplying by $\frac{1}{2}$ ; dividing by 37 is the same as multiplying by $\frac{1}{37}$ , and so on.

Let’s look at why dividing by a fraction is the same as multiplying by its reciprocal.

To find $\frac{1}{3}$ ; of 12, we divide by 3.

$12 \div 3 = 4$ .

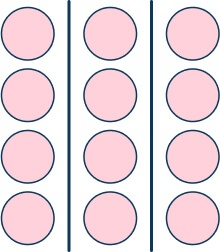
‘Of’ can mean multiply, so $\frac{1}{3}$ of $12 = \frac{1}{3} × 12 = \frac{1}{3} × \frac{12}{1} = \frac{12}{3} = 4$ .

Now think about $\frac{2}{5} ÷ 2$ .

If we represented this in a similar way to above, it would look like this: $\frac{2}{5}$ shaded (initially shaded in light green), then each fifth halved (shaded in dark green), so the answer is $\frac{2}{10}$ , or $\frac{1}{5}$ in its simplest form.

However, as the divisor is a factor of the numerator, we could also visualise this division like this: shading 2 fifths (initially in light green) and then finding half of that amount (in dark green), which is $\frac{1}{5}$ .

This second method (dividing the numerator by the divisor) can be used in any fraction division where the divisor is a factor of the numerator, as it skips an unnecessary step and removes the stage of knowing how to simplify fractions. For example:

$\frac{3}{7} ÷ 3 = \frac{1}{7}$ (which, using the first method, would be $\frac{3}{7} × \frac{1}{3} = \frac{3}{21} or \frac{1}{7}$ )

$\frac{8}{9} ÷ 2 = \frac{4}{9}$ (or $\frac{8}{9} × \frac{1}{2} = \frac{8}{18}$ or $\frac{4}{9}$ )

$\frac{15}{17} ÷ 5 = \frac{3}{17}$ (or $\frac{15}{17} × \frac{1}{5} = \frac{15}{85}$ or $\frac{3}{17}$ )

Dividing fractions by fractions

When fractions are divided by proper fractions (fractions smaller than 1), they become bigger. The answer could be an improper fraction (or mixed number) or an integer. We can divide a fraction by a fraction by using an equivalent multiplication calculation. For example, dividing by $\frac{1}{2}$ and multiplying by 2 give the same result.

Let’s see how this works.

\frac{1}{2} ÷ 4 = \frac{1}{8}

Dividing by $4$ is the same as multiplying by $\frac{1}{4}$ , or finding $\frac{1}{4}$ of.

\frac{1}{2} ÷ 2 = \frac{1}{4}

Dividing by $2$ is the same as multiplying by $\frac{1}{2}$ , or finding $\frac{1}{2}$ of.

\frac{1}{2} ÷ 1 = \frac{1}{2}

Dividing by $1$ is the same as multiplying by $1$ .

$\frac{1}{2} ÷ \frac{1}{2} = \frac{2}{2}$ , or $1$

Dividing by $\frac{1}{2}$ is the same as multiplying by 2.

$\frac{1}{2} ÷ \frac{1}{4} = \frac{4}{2}$ , or 2

Dividing by $\frac{1}{4}$ is the same as multiplying by 4.

$\frac{1}{2} ÷ \frac{1}{8} = \frac{8}{2}$ , or 4

Dividing by $\frac{1}{8}$ is the same as multiplying by 8.

Look at the pattern below: as the divisor halves, the quotient doubles.

32 \div 32 = 1

32 \div 16 = 2

32 \div 8 = 4

32 \div 4 = 8

32 \div 2 = 16

32 \div 1 = 32

This is true of any division calculation – see the sequence below (the same sequence represented in the bar models above).

\frac{1}{2} ÷ 4 = \frac{1}{8}

\frac{1}{2} ÷ 2 = \frac{1}{4}

\frac{1}{2} ÷ 1 = \frac{1}{2}

$\frac{1}{2} ÷ \frac{1}{2} = \frac{2}{2}$ , or 1

$\frac{1}{2} ÷ \frac{1}{4} = \frac{4}{2}$ , or 2

$\frac{1}{2} ÷ \frac{1}{8} = \frac{8}{2}$ , or 4

Similar to dividing by integers, to divide by a fraction you can multiply by the reciprocal of the second fraction (to find the reciprocal of a fraction, invert it – the reciprocal of $\frac{1}{3}$ is $\frac{3}{1}$ , which is the same as 3).

For example, dividing by $\frac{1}{2}$ is the same as multiplying by 2; dividing by $\frac{1}{37}$ is the same as multiplying by 37, and so on.

So $\frac{1}{2} ÷ \frac{1}{2}$ is the same as $\frac{1}{2} × 2$ , or $\frac{1}{2}$ of 2, which is $\frac{2}{2}$ , or 1.

$\frac{1}{2} ÷ \frac{1}{4}$ is the same as $\frac{1}{2} × 4$ , or $\frac{1}{2}$ of 4, which is $\frac{4}{2}$ , or 2.

A Third Space Learning online lesson on how to divide fractions. — A Third Space Learning online lesson on dividing fractions by using equivalent multiplication calculation.

How to divide fractions: tips for teachers

It’s often best to begin with dividing fractions where the divisor is a factor of the numerator; this is a good introduction to fraction divisions as pupils already know how to divide this way. Encourage your pupils to think about the denominator as a name for the fraction, rather than a value to be divided. For example, if calculating $\frac{3}{5} ÷ 3$ , start by writing “3 bananas ÷ 3”. Then swap out the word “bananas” for “fifths”, to become “3 fifths ÷ 3”. This should consolidate the idea that the denominator tells us about the size of the fraction, not the quantity we have.

Once your pupils have understood this step, then move onto examples where the divisor isn’t a factor of the numerator – for example, $\frac{2}{5} ÷ 3$ . Using bar models (as demonstrated above), show the pupils how divisions like this can be calculated.

If pupils don’t properly understand the process, they often end up dividing the wrong part of the fraction. For example, with $\frac{1}{6} ÷ 2$ , pupils may see that 6 can be divided by 2 and answer as $\frac{1}{3}$ . Or with $\frac{4}{8} ÷ 2$ , they may divide both the numerator and denominator and answer with $\frac{2}{4}$ .

Some teachers use ‘KCF’, or ‘Keep, Change, Flip’ to teach dividing fractions. This means you keep the first fraction the same, change the division sign to a multiplication sign, and then ‘flip’ the divisor (find the reciprocal). Whilst this does yield the correct answer, it is important that if you choose to use this ‘method’, it is only once pupils fully understand the process of dividing fractions – are they just working through an abstract checklist of instructions, or do they know why they’re doing what they’re doing?

Once pupils have mastered this of dividing fractions, they can apply it to fraction games and real-life examples to further consolidate their knowledge.

How to divide fractions examples

In this circle, each shaded part is $\frac{1}{5}$ of the area of the circle. The two white parts have equal areas. What fraction of the circle is one of the white areas?

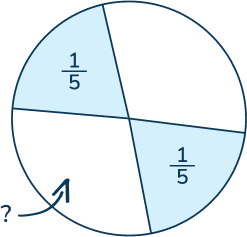
The shaded area totals $\frac{2}{5}$ , so the remaining white area must represent $\frac{3}{5}$ of the total. As they are equal sizes, to calculate the size of one white area, we must divide $\frac{3}{5}$ by 2. $\frac{3}{5} ÷ 2 = \frac{3}{5} × \frac{1}{2} = \frac{3}{10}$ .

$\frac{3}{4} ÷ ? = \frac{3}{12}$
If we think of this as a multiplication, it would read $\frac{3}{4} × ? = \frac{3}{12}$ . We know that to multiply fractions, we multiply both the numerators and the denominators, so in this number sentence, the missing fraction is $\frac{1}{3}$ , as $\frac{3}{4} × \frac{1}{3} = \frac{3}{12}$ . Multiplying by $\frac{1}{3}$ is the same as dividing by 3, so the missing number is 3.

3. Ben ate $\frac{1}{4}$ of a pizza. Four other pupils shared the remainder equally. What fraction of the pizza did each of the other pupils get?
If Ben ate $\frac{1}{4}$ , there is $\frac{3}{4}$ left. $\frac{3}{4}$ divided between 4 pupils is the same as $\frac{3}{4} × \frac{1}{4}$ , which is $\frac{3}{16}$ .

When do pupils learn to divide fractions?

Pupils aren’t expected to divide fractions until year 6, where they should be taught to “divide proper fractions by whole numbers [for example, $\frac{1}{3} ÷ 2 = \frac{1}{6}$ . Division of fractions by other fractions isn’t an expectation of primary school maths. When it comes to KS2 fractions, the national curriculum only requires that pupils be taught to divide fractions by integers.

How to divide fractions: practice questions

Anisa ate $\frac{1}{5}$ of a cake. Three of her friends shared the leftovers equally. What fraction of the cake did they each eat?
$\frac{4}{15}$

$\frac{?}{?} ÷ 5 = \frac{2}{13}$

$\frac{10}{13}$

Mrs Smith uses ⅔ of a roll of wrapping paper to wrap five presents of equal size. What fraction of the roll of wrapping paper does each present use?
$\frac{2}{15}$

$\frac{8}{9} ÷ 4 =$

$\frac{2}{9}$

In this rectangle, the shaded part is 1/8 of the area of the rectangle. The two white parts have equal areas. What fraction of the rectangle is one of the white areas?

$\frac{7}{16}$

Frequently asked questions

1. How do you divide and multiply fractions?

To divide a fraction by an integer, multiply the fraction by the reciprocal of the integer. For example, to divide $\frac{1}{3}$ by 2, calculate $\frac{1}{3} × \frac{1}{2}$ .
To multiply fractions, multiply the numerators and denominators. For example, $\frac{1}{3} × \frac{1}{2} = \frac{1}{6}$ because $1 \times 1$ (the numerators) $= 1$ , and $3 \times 2$ (the denominators) $= 6$ .

2. When you divide a fraction do you flip it?

To divide a fraction, we can find the reciprocal of the divisor and then multiply the first fraction by that reciprocal. When you ‘flip’ a fraction, you’re finding its reciprocal. For example, to find the reciprocal of $\frac{1}{2}$ , ‘flip’ it to become $\frac{2}{1}$ , or 2; to find the reciprocal of 3, or $\frac{3}{1}$ , ‘flip’ it to become $\frac{1}{31}$ .

3. Why can’t you divide fractions?

You can divide fractions! When you divide a fraction by an integer (whole number), it gets smaller. We are used to things getting smaller when they are divided. However, if you divide a fraction by another fraction, it gets bigger! This is so long as the second fraction is under 1 – also known as a proper fraction.

DO YOU HAVE PUPILS WHO NEED MORE SUPPORT IN MATHS?

Every week Third Space Learning’s specialist primary maths tutors support thousands of students across hundreds of schools with weekly online 1 to 1 maths lessons designed to plug gaps and boost progress.

Since 2013 these personalised one to one lessons have helped over 150,000 primary and secondary students become more confident, able mathematicians.

Learn about the scaffolded lesson content or request a personalised quote for your school to speak to us about your school’s needs and how we can help.