What Is A Mixed Number: Explained for Primary School
Mixed numbers and improper fractions are introduced once children are secure in their understanding of proper fractions (unit- and non-unit) in Upper KS2.
What is a mixed number?
A mixed number, sometimes also called a mixed fraction, is a combination of an integer (whole number) and fraction (part of a whole number).
Examples of mixed numbers
Mixed numbers can be written with or without ‘and’, e.g. 5 and ¾ or 5¾. The fractional part of the mixed number must be a proper fraction (less than one whole). In a proper fraction, the numerator (top number) is less than the denominator (bottom number), such as 3⁄7, or 11⁄15. A mixed number cannot be composed of an integer and an improper fraction (more than one whole), such as 5 and 5⁄4. This would have to be corrected to a mixed number – in this case, it would be 6 and ¼.
When do children learn about mixed numbers in the national curriculum?
Children first encounter mixed numbers in UKS2. In Year 5, pupils must “recognise mixed numbers and improper fractions and convert from one form to the other and write mathematical statements > 1 as a mixed number (for example, 2⁄5 + ⅘ = 6⁄5 = 1 and ⅕)” and “multiply proper fractions and mixed numbers by whole numbers, supported by materials and diagrams”.
Finally, in Year 6 maths lessons, pupils will be “adding and subtracting fractions with different denominators and mixed numbers, using the concept of equivalent fractions”.
How do mixed numbers relate to other areas of maths?
Mixed numbers often appear in measurement topics, requiring children to convert between units of measure. For example, children would be expected to know that 1½ litres is equivalent to 1,500ml, or that 2¾ hours = 165 minutes. Some mixed numbers may require simplifying, e.g. 4 2⁄4 = 4½. These types of measures will also sometimes be represented as decimals, such as 1.5 or 2.75, as children are expected to know fraction-decimal equivalents in UKS2.
How are mixed numbers used in real life?
Children should be shown how the maths they are learning is applicable in real-life contexts. Therefore, as previously mentioned, mixed numbers can be most commonly found in real-life when referring to units of measure, e.g. 1½ tablespoons, 1¾ hours, 5½ pizzas, etc.
Fractions Lessons Resource Pack
Download a free pack of worksheet on fractions, including questions on mixed numbers and word problems.
Download Free Now!3 worked examples for mixed number
1) Convert between mixed numbers and improper fractions
To convert an improper fraction to a mixed number, you’ll need to understand how to divide fractions. The process will involve dividing the numerator (in a division, this is also known as the dividend) by the denominator (also known as the divisor). The answer to this (also known as the quotient) becomes the whole number part; the remainder (if there is one) becomes the numerator; the denominator (which was the divisor) remains the same.
For example, to convert 23⁄5 to a mixed number, step-by-step:
- Divide 23 by 5.
- 5 fits into 23 4 whole times, so the whole number is 4.
- There is a remainder of 3, so the new numerator is 3 in the fraction part of the mixed number (the denominator remains the same as the original improper fraction). The answer is therefore 4⅗.
This can be much more clearly visualised with a diagram such as a bar model:
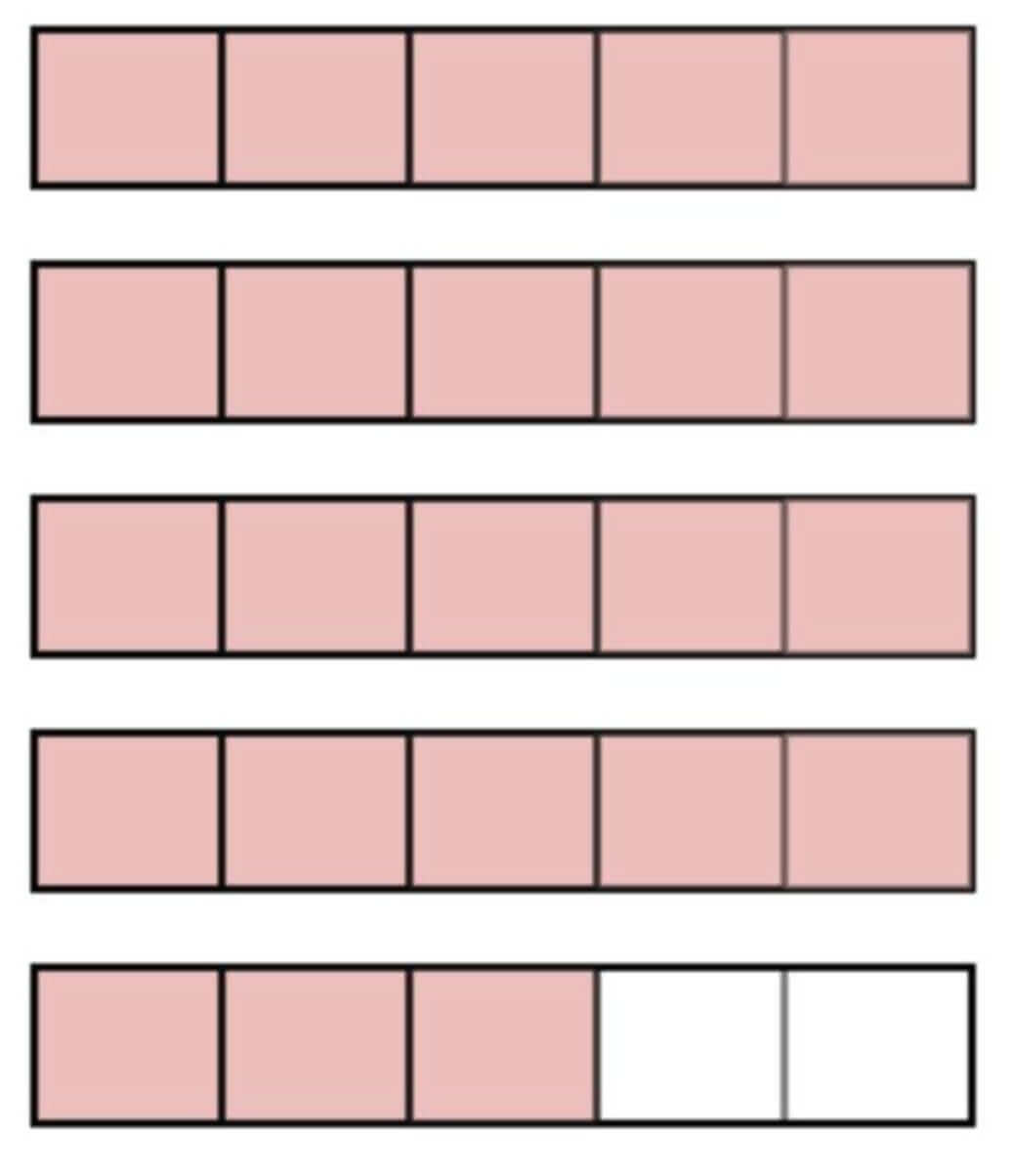
As shown above, twenty-three fifths can also be written as four wholes and three-fifths.
To convert a mixed number to an improper fraction, multiply the whole number by the denominator and add the numerator. The answer to this becomes the new numerator; the denominator remains the same.
For example, to convert 2⅔ to an improper fraction step-by-step:
- 2 (whole number) x 3 (denominator) = 6
- 6 + 2 (numerator) = 8 (the new numerator). The answer is therefore 8⁄3.
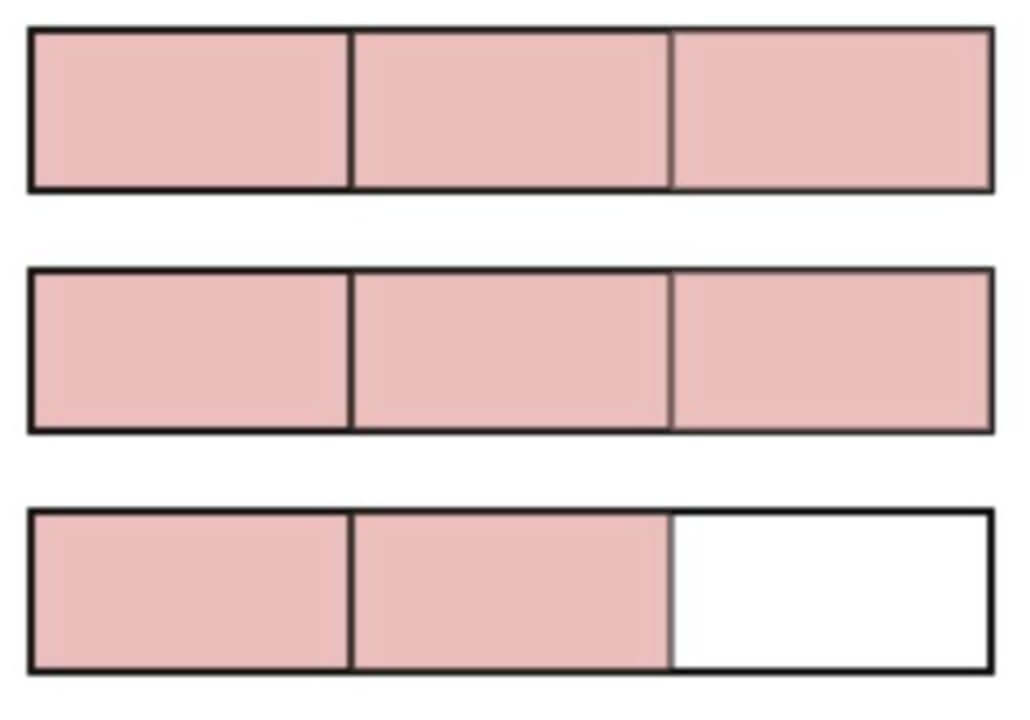
As shown above, two wholes and two-thirds can also be written as eight-thirds.
2) Add or subtract mixed numbers
Example 1: 1¼ + 1½ Example 2: 2⅓ – 1⅖
An addition or subtraction such as these can be approached in one of two ways:
- by first partitioning the mixed numbers into integers and proper fractions, calculating and then recombining, such as example 1 above: 1 + 1 = 2, ¼ + ½ = ¾, then 2 + ¾ = 2¾
- by first converting the mixed numbers into improper fractions, calculating and then converting back into mixed numbers if necessary, such as example 2 above: 2⅓ – 1⅖ = 7⁄3 – 7⁄5 = 35⁄15 – 21⁄15 = 14⁄15
Read more: How To Add Fractions: Step By Step Guide
3) Multiply mixed numbers by whole numbers
1⅓ x 5
As above, this can approached in one of two ways:
- by first partitioning the mixed number into an integer and proper fraction, calculating and then recombining: 1 x 5 = 5, ⅓ x 5 = 1⅔, 5 + 1⅔ = 6⅔
- by first converting the mixed number into an improper fraction, calculating and then converting back into a mixed number if necessary: 1⅓ = 4⁄3, 4⁄3 x 5 = 20⁄3 = 6⅔
5 mixed number practice questions and answers
- 2½ + 1⅗
Answer = 5⁄2 + 8⁄5 = 25⁄10 + 16⁄10 = 41⁄10 = 4 and 1⁄10 - 3 x 2⅖
Answer = 3 x 12⁄5 = 3⁄5 = 7⅕ - The length of a day on Earth is 24 hours. The length of a day on Mercury is 58⅔ times the length of a day on Earth. What is the length of a day on Mercury, in hours? (2018 SATs)
Answer: 24 x 58⅔ = 1,408 hours - Which improper fraction is equivalent to 6⅞?
67⁄8 48⁄8 62⁄8 55⁄8 76⁄8 (2018 SATs)
Answer: 55⁄8 - Potatoes cost £1.50 per kg and carrots cost £1.80 per kg. Jack buys 1½kg of potatoes and ½kg of carrots. How much change does he get from £5? (2019 SATs)
Answer: £1.50 x 1½ = £2.25, ½ of £1.80 = 90p, £2.25 + 90p = £3.15
Read more about adding, subtracting and and learning how to multiply fractions in this fractions for kids article.
Both are larger than one whole but are represented differently: an improper fraction has only a numerator and a denominator (the former of which is larger than the latter, e.g. 5⁄3, the equivalent of 1⅔); a mixed number has a whole number and a proper fraction (e.g. 1⅔, the equivalent of 5⁄3).
See the ‘worked examples’ section above
Read more: How to Teach Fractions: adding, subtracting, multiplying and dividing fractions.
For more explanations teaching primary maths topics, see our Primary Maths Dictionary
DO YOU HAVE PUPILS WHO NEED MORE SUPPORT IN MATHS?
Every week Third Space Learning’s specialist primary maths tutors support thousands of students across hundreds of schools with weekly online 1 to 1 maths lessons designed to plug gaps and boost progress.
Since 2013 these personalised one to one lessons have helped over 150,000 primary and secondary students become more confident, able mathematicians.
Learn about the scaffolded lesson content or request a personalised quote for your school to speak to us about your school’s needs and how we can help.