Teaching Decimals KS2: A Guide For Primary School Teachers From Year 4 To Year 6

Decimals in KS2 are a new topic to most primary school pupils. While they will have encountered some related topics like fractions, decimals themselves are a different way of looking at numbers than they are used to.

This blog will focus on decimals within the ‘Fractions (including decimals)’ section of the National Curriculum and provide tips and tricks for helping your pupils approach them with confidence.

Teaching Decimals KS2

Decimals are first mentioned explicitly in the National Curriculum at KS2, though it is not straightforward to work out when and how to teach decimals due to some contradictions and omissions within the guidance

For example, in Year 3 there is the mention of understanding tenths, but it is not made clear if this refers to just fractions or decimals as well. You will need to look at the non-statutory notes to see that it does refer to decimals. But as this is non-statutory does it need to be followed?

Further confusion is sown when, in the measurement part of the National Curriculum for Year 3, students are required to solve money problems involving £ and p. Of course, to do this successfully, the students need to be aware of not only tenths but hundredths, which is not a requirement until Year 4.

It is worth the Year 3 teacher bringing this to the attention of the maths lead in the school to highlight the discrepancy and come up with a plan that suits their school.

The Theory

Note: As there is such an overlap between decimals, place value and fractions, it is suggested that you look at those blogs to get a strong sense of the development of teaching decimals.
Place Value KS2
Fractions KS2

It should be clear from the outset that the principles behind the teaching of fractions and place value are the same as those for the teaching of decimals. The role of the teacher is to make the connection between these two areas explicit for students so that they can see that decimals are merely a continuation of these ideas and not something completely new.

It is by drawing the attention of pupils to these connections that we can drastically reduce the teaching time required to teach maths concepts and increase the chances of pupils achieving mastery. 

Decimals Year 3

In the National Curriculum for maths in England, for each area of maths outlined, there is both a statutory requirement and a non-statutory guidance. The statutory requirement in KS2 maths is as follows:

• Count up and down in tenths; recognise that tenths arise from dividing an object into 10 equal parts and in dividing one-digit numbers or quantities by 10 

Non-statutory notes and guidance: 

• Pupils connect tenths to place value, decimal measures and to division by 10. 

Decimals Lesson Ideas Year 3

As students only need to count up and down in tenths much of the practice can be done with a counting stick at the beginning of lessons or in Maths Meetings if you school uses those.

It is always worth some initial explicit teaching to begin with, however. Dienes blocks are a useful manipulative to do this as students will be familiar with them though you could also use Cuisenaire rods if students are familiar with those too.

Students will be quite comfortable with this block representing 10 and would have learnt about tenths in fractions.

We can tell students that when we want to discuss numbers between integers we can use fractions, but we can also use decimal numbers.

At this stage, I, as the teacher would count up in tenths as fractions to recap prior learning and get the students to do this afterwards. Each time adding a 1/10 block each time. 

Once the students have done this, I would then count again but use decimals. I may model this 2 or 3 times before giving students an opportunity to do so. They could count whole class first and then move to counting with a partner etc. 

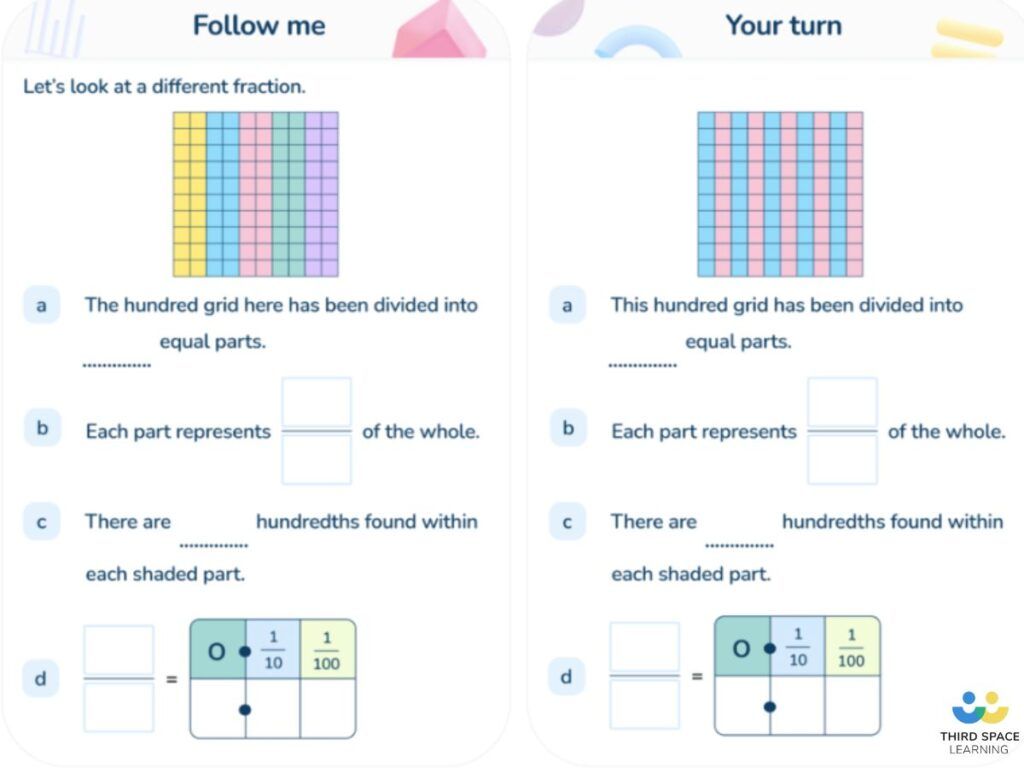
Once students have had some familiarity with counting up decimals up to 1 from zero, I would show them how we write a decimal number. I would use a place value chart with ones and tenths and explain that when we write a number that has digits to the right of the ones, we use a decimal point to show that we want to represent a number smaller than ones. 

Next, I would use a place value counter to show what a decimal looks like. Drawing attention to the fact that the zero represents the ones and the decimal point tells us that we are looking at numbers less than zero.

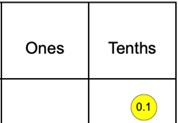
Continue building up with the students counting until you get to 0.9. At this point you could ask students what they think will happen with the addition of one more 0.9. Here they would need to transfer their knowledge of place value and from the counting earlier on in the lesson. 

Explain to students that the rules of place value do not alter and when the numeral 9 is represented then the next step is to go the following place value to the left.

Here students would get the opportunity to work in pairs counting forwards using place value grids and counters. They can be challenged by getting them to count backwards from 1 in steps of 0.1 or asking them to continue counting from a randomly chosen tenth.

It is also best to get students to practice using a range of manipulatives. Tens frames can provide a good mental model for counting in tenths.

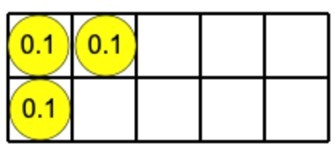
Counting sticks provide an additional model and are useful to support the counting of tenths quickly at some point during the lesson.

As an activity, I would want student to focus on the link between decimals and fractions and so getting student to complete a table where they need to write an image, write in words, write a fraction or write in decimals a given decimals number. 

Where possible, relate the counting up in decimals to real life context such as 10p’s in pounds or millimetres to cm etc.

This would then be something I would then repeat again as the start of other lessons to keep this knowledge fresh in the mind of the students.  

Decimals Word Problems Year 3

Jake and Jack are counting to 1 in tenths. Jack is counting in fractions and Jake is counting in decimals. Will they say 5/10 and 0.5 at the same time?

Here, students need to understand that 5/10 and 0.5 are equivalent to each other and so these would be said at the same time. 

Encourage students to write a number line in both fractions and decimals in tenths so that they can see this if they are struggling. 

Decimals: Reasoning and Problem Solving Year 4

A typical reasoning/ problem solving activity may look like the following:

A common error for students to make is that after 0.9 they say ‘zero point ten’ as they forget about the rules of place value. As we can see from the above, that mistake has been made. Students should be able to identify this error and explain, using their knowledge of place value, why this is incorrect. 

Decimals Year 4

In the National Curriculum for maths in England, for each area of maths outlined, there is both a statutory requirement and non-statutory guidance. The statutory requirement is as follows:

• Recognise and write decimal equivalents of any number of tenths or hundredths 
• Recognise and write decimal equivalents to 1/4, 1/2, 3/4 
• Find the effect of dividing a one- or two-digit number by 10 and 100, identifying the value of the digits in the answer as ones, tenths and hundredths 
• Round decimals with one decimal place to the nearest whole number 
• Compare numbers with the same number of decimal places up to two decimal places 
• Solve simple measure and money problems involving fractions and decimals to two decimal places. 

Non-statutory notes and guidance: 

• Pupils should connect hundredths to tenths and place value and decimal measure. 
• Pupils are taught throughout that decimals and fractions are different ways of expressing numbers and proportions. 
• Pupils’ understanding of the number system and decimal place value is extended at this stage to tenths and then hundredths. This includes relating the decimal notation to division of whole number by 10 and later 100. 
• They practise counting using simple fractions and decimals, both forwards and backwards. 
• Pupils learn decimal notation and the language associated with it, including in the context of measurements. They make comparisons and order decimal amounts and quantities that are expressed to the same number of decimal places. They should be able to represent numbers with one or two decimal places in several ways, such as on number lines. 

Decimals Activities Year 4

For this lesson I will focus on the objective ‘recognise and write decimal equivalents to 1/4, 1/2, 3/4.’

Students should be familiar with these fractions from work across KS1 and Year 3. As mentioned in the ‘theory of teaching decimals’ section, our job is to make links between content explicit and to ensure that students attend to these links.

Many students across the country when learning fractions will have used a fraction wall like the one below.  

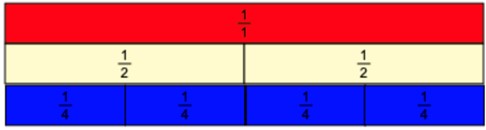
These are useful to demonstrate the fractional equivalence between different fractions as well as for supporting basic arithmetic with the use of fractions, particularly when the denominators are the same. If pupils are fluent with this is resource, then a simple tweak allows the teacher to bring the relationship between decimals and fractions to life.

By replacing the fractions with decimals on the same resource, students will be able to apply what they know already about the resource into the new context. Personally, I feel giving students access to both side-by-side brings the most benefits to students thinking about the mathematical content.

Asking students ‘What is the same? What is different?’ is a powerful question. This is far from ‘discovery learning.’ Careful consideration has gone into the resource and there are plenty of pre-planned questions with small activities to ensure that the relationship becomes clear.

Questions that can bring about mathematical thinking could include:

• What happens if you swap a ½ for a 0.5?
• How many 0.5 strips are equivalent to ¼?
• What do you notice if you place all the 0.25 strips under the ¼ strips?
• What do you get if you take one of those 0.25 strips and ¼ strips away?
• Is there are ½ strip that is equal to three 0.25 strips?
• What happens if I place a 0.5 strip after both ½ strips?

Clearly these questions are not the only questions that one could ask, but they demonstrate the importance of planning such questions and activities in advance to ensure that our students are thinking deeply about primary mathematics.

Decimals Word Problems Year 4

A typical word problem in Year 4 involving decimals would be something like the following:

A chocolate bar sells for ¾ of a pound. What is the price in pence?

This question aims to give students a context for the learning of decimal and fractional equivalences. Students would need to apply their new learning to their understanding of money to deduce that it would cost 0.75p. 

Decimals: Reasoning and Problem Solving Year 4

This open-ended task allows students to really conjecture using their understanding of decimal and fractional equivalence and knowledge of decimal numbers. 

Any number between 0.0 and 0.49 is clearly an acceptable answer and the idea of this task is that pupils write something down to that effect and. We should not deter efficiency when communicating our mathematics. Common errors that students make is forgetting about hundredths* when providing their answer and so this is something that is worth reminding pupils. 

Of course, this could be extended to which decimal numbers are greater than one half but less than one etc.

*Some students may be familiar with thousandths at this point and so allowing them to explain their understanding of the question within the context of thousandths should also be allowed.

When explaining the answer, I would also mention that there are infinite numbers that can appear after the decimal point but as they have only learnt about numbers with hundredths, this is an acceptable answer at this stage, but they will learn about other decimal place value at a later stage.

Decimals Year 5

In the National Curriculum for maths in England, for each area of maths outlined, there is both a statutory requirement and a non-statutory requirement. The statutory requirement is as follows:

• Read and write decimal numbers as fractions [for example, 0.71 = 71/100] 
• Recognise and use thousandths and relate them to tenths, hundredths and decimal equivalents 
• Round decimals with two decimal places to the nearest whole number and to one decimal place 
• Read, write, order and compare numbers with up to three decimal places 
• Solve problems involving number up to three decimal places

Non-statutory notes and guidance:

• Pupils should be taught throughout that percentages, decimals and fractions are different ways of expressing proportions. 
• They extend their knowledge of fractions to thousandths and connect to decimals and measures. 
• Pupils extend counting from year 4, using decimals and fractions including bridging zero, for example on a number line. 
• Pupils say, read and write decimal fractions and related tenths, hundredths and thousandths accurately and are confident in checking the reasonableness of their answers to problems. 
• They mentally add and subtract tenths, and one-digit whole numbers and tenths. 
• They practise adding and subtracting decimals, including a mix of whole numbers and decimals, decimals with different numbers of decimal places, and complements of 1 (for example, 0.83 + 0.17 = 1). 
• Pupils should go beyond the measurement and money models of decimals, for example, by solving puzzles involving decimals. 
• Pupils should make connections between percentages, fractions and decimals  and relate this to finding ‘fractions of’. 

Decimals Activities Year 5

For this lesson I will focus on the objective ‘round decimals with two decimal places to the nearest whole number and to one decimal place.’ 

This objective looks at many mathematical ideas and where appropriate, such objectives should be broken down into smaller manageable ones. It might be the case that the objective as written in the National Curriculum, is not fully reached until after a sequence of lessons. For the remaining part of this section, it will focus on rounding decimals with two decimal places to one decimal place.

Note that this objective builds on from the Year 4 objective ‘round decimals with one decimal place to the nearest whole number.’ Therefore, before teaching this new content, it would be sensible to check for the prerequisites and see if students are able to do it. If they cannot, then ploughing ahead with the objective from the Year 5 section will be futile. For the sake of this blog, assume that students do have this prerequisite knowledge. 

Place value counters and empty number lines are useful resources to teach this concept. 

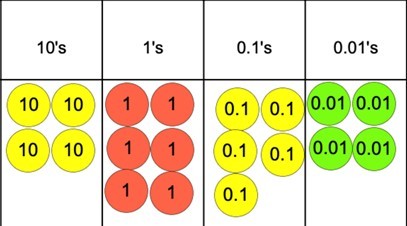
Students should be able to look at a place value chart like the one above and identify what the number being shown is. In this case 46.54.

As the objective is to round to the nearest tenth, a discussion needs to take place between what the possible numbers these may be. Language is important here. Quite often, when the term ‘round down’ is used students take this to mean that the place value that we seek to round moves decreases.

This is due to the connotation of the word ‘down’ and its link to  something getting smaller and when we round up, there is a change in the digit within the place value. It is crucial that students understand that the process of rounding down means that the place value that we wish to round to remains the same.

The place value chart helps here as students will know that when we round to the ‘nearest’ then the digits all numbers to the right of what we are rounding to will be zero. Whereas the digits to the left of the place value we are rounding to remain the same, This can be identified using the place value chart and counters. 

We can see that the 10s and 1s will remain the same and the 0.01s will become zero (in the case of decimals, the zero does no need to be written as it is implied). It can be drawn out the possible numbers that 46.54 could be rounded to would either be  46.5 or 46.6.

Writing these either side of a empty number line is useful for the development of students conceptual understanding.  It should be noted that this is one place where students can come undone when rounding and so giving students plenty of practice in identifying the potential rounded numbers either of the original number is often required.

The next step would be for students to place the original number on to the empty number line.

Here students can then use both visual representations, along with their knowledge of rounding rules to deduce that the answer must be 46.5 as 46.54 is closer to it and it can be seen from the place value chart that as there are four 0.01s this number is then rounded down.

Decimals Word Problems Year 5

A suitable word problem would be like the following:

Chris is measuring the length of a wall. He rounds his answer to 4 metres. What is the smallest length that the will could be?

This question checks students understanding of the limits in which something can be either rounded up or down. Here they need to determine that the shortest length the wall could be would be 3.5 metres long as anything smaller than this would be rounded down to 3 metres.

Decimals: Reasoning and Problem Solving Year 5

Shannen is thinking of a number. When rounded to the nearest whole, the answer is 6. When rounded to the nearest tenth the answer is 5.9. What could Shannen’s number be?

Here students need to consider the differences between rounding between two different values and how this affects possible answers. They may deduce that the whole in the number will be 5 as this, followed by a tenth value above 5 would round to 6 and fulfil the requirement when rounding to the nearest tenth where the whole must remain a 5.

Secondly, in regards to the decimals, students need to know the greatest and least number where one could round up or down from to still get 5.9.

Answers: Any numbers between 5.85 and 5.94.

Decimals Year 6

In the National Curriculum for maths in England, for each area of maths outlined, there is both a statutory requirement and a non-statutory requirement. The statutory requirement is as follows:

• Associate a fraction with division and calculate decimal fraction equivalents [for 3 example, 0.375] for a simple fraction [for example, 3/8] 
• Identify the value of each digit in numbers given to three decimal places and multiply and divide numbers by 10, 100 and 1000 giving answers up to three decimal places 
• Multiply one-digit numbers with up to two decimal places by whole numbers 
• Use written division methods in cases where the answer has up to two decimal places 

Non-statutory notes and guidance: 

• They practise calculations with simple fractions and decimal fraction equivalents to aid fluency, including listing equivalent fractions to identify fractions with common denominators. 

Pupils can explore and make conjectures about converting a simple fraction to a decimal fraction (for example, 3 ÷ 8 = 0.375). For simple fractions with recurring decimal equivalents, pupils learn about rounding the decimal to three decimal places, or other appropriate approximations depending on the context.

Pupils multiply and divide numbers with up to two decimal places by one-digit and two-digit whole numbers. Pupils multiply decimals by whole numbers, starting with the simplest cases, such as 0.4 × 2 = 0.8, and in practical contexts, such as measures and money. 

Pupils are introduced to the division of decimal numbers by one-digit whole number, initially, in practical contexts involving measures and money. They recognise division calculations as the inverse of multiplication. 

Pupils also develop their skills of rounding and estimating as a means of predicting and checking the order of magnitude of their answers to decimal calculations. This includes rounding answers to a specified degree of accuracy and checking the reasonableness of their answers. 

Decimals Lesson Ideas Year 6

For this lesson I will focus on the objective ‘identify the value of each digit in numbers given to three decimal places and multiply and divide numbers by 10, 100 and 1000 giving answers up to three decimal places.’  This is will be something that students will have slowly built up to across KS2 when learning multiplication as well as their learning about decimals.

While many teachers I am sure are familiar with the use of place value charts and counters to multiply and divide numbers, this lesson will look at the use of an underused resource in the primary classroom – a Gattegno chart.

Ideally this will have been introduced when students first learn about multiplying and dividing  by 10, 100 or 1,000 etc but if not, it can still prove to be a way to extend students thinking. 

When selecting a Gattegno chart to use in the classroom, it is important that care is taken to make sure that the right one is chosen. Consider the two charts below. Which one do you believe is better to use in the classroom?

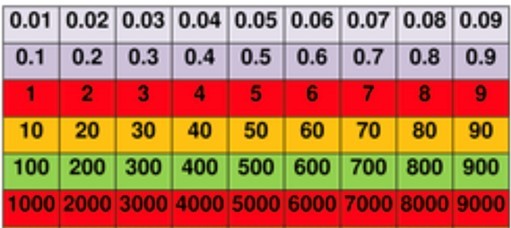
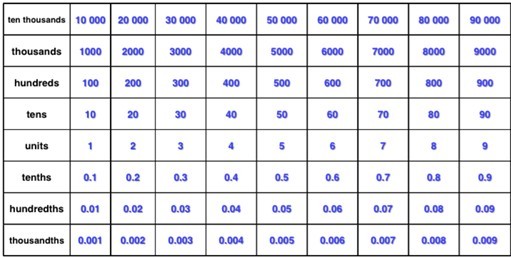
For me, the chart from Andrew Jefferey’s website is superior to the one from TES, as the bottom row of numbers are the smallest and as you go up (an embedded movement that we associated with getting bigger) the numbers indeed get bigger.

Contrast this with the one in TES where it is a downwards movement that results in the numbers increasing.

To use the chart, simply place counters on the square of the number that you wish to make. For example, if I wanted to make the number 5.31, I would place a counter on 5, a counter on 0.3 and a counter on 0.01. It is here we see that the chart supports the mathematical skill of partitioning numbers. 

Once students have decided on a number, a partner can then decide if the number will be multiplied or divided and by what power of 10. The person who decided on the original number must then move the counters to demonstrate this.

For example, if the number above had to be multiplied by 100, the person who placed the counters would have to rearrange them so that they created the product of the original number multiplied by 100. In this case, that would mean moving all the counters up two places. This would give the answer 531.

Conversely, if you had to then divide the number 1000, then the counters would have to be moved down 3 spaces. This would give 0.531.

Decimals Word Problems Year 6

 A typical Year 6 word problem would be like the following:

The population of London is 8.961 million. The population of England is nearly 6 times as much. What is the population of England to two decimal places?

This is a two-step problem that requires students to multiply 8.961 million by 6. Here students should use a formal written method to support their thinking. The answer would be 53.586 million.

The next step would be to round this answer to the nearest two decimal places which would give 53.59 million or 53,590,000.

Decimals: Reasoning and Problem Solving Year 6

A possible reasoning and problem-solving activity that students could do in pairs would be to find a way to get from a given number to another number using the chart in as few moves as possible.

For example, students may need to go from 5.532 and get to 9.909. To increase the difficulty, you could put in rules such as all 4 operations must be used at least once. Or only 2 counters can be moved at any one time. There are many options available to increase the difficulty of this task.

This type of activity is ideal for assessment for learning as it makes you see just how well a student’s grasp of the number system and laws of arithmetic really are.

Decimals can be a difficult topic for pupils to get their heads around. Hopefully this post has given you some good ideas to help your pupils approach it with confidence, no matter which KS2 year they are in!