Teaching Place Value KS2: A Guide For Primary School Teachers From Year 3 To Year 6
Place value is usually the first thing topic taught in KS2 maths, whether you’re a Year 3 or a Year 6 teacher, because it’s such an important basis for understanding any other primary maths topic.
In this article for Key Stage 2 teachers, Neil Almond explains how you can ensure your pupils have a deep and coherent understanding of place value, through a consistent mastery approach to teaching it.
What is place value?
Place value is the value of each digit in a number (e.g. the 3 in 37 stands for 30).
At Key Stage 1, pupils are required to learn place values for numbers up to 100, including recognising the place value of any digit in a two-digit number.
They’re also required to learn how to use place value and associated number facts to solve rudimentary maths problems.
Place value at Key Stage 2 develops this understanding to handle larger numbers and the relative values of each digit depending on where it appears in the number. It is expected that by the end of Year 6, pupils will be able to identify the place value of digits in numbers up to 10,000,000 – and solve problems accordingly.
Third Space Learning has also produced a simple guide to place value for children!
Teaching place value at KS2: the basics
It’s not an exaggeration to say that an understanding of place value is an absolutely key concept for students to grasp; it is the foundation of our 10-base number system and the four operations.
This journey begins in the earliest mathematical experiences of students, particularly those experiences in Key Stage 1 where the place value system is taught more explicitly.
As this is only a guide to the progression in teaching KS2 place value, it is imperative that teachers (particularly those that teach Year 3) go back to the national curriculum objectives laid out for KS1 and ensure that students are able to meet those.
Read more: Quick Guide to KS1 and KS2 Place Value Learning Objectives
Children who do not understand that there is a limit to the value that can be represented using only tens and ones, will not understand this when dealing with more bases.
This is why you can often find the misconception of ‘a hundred and one’ written as 1001. Students must enter Key Stage 2 with a conceptual understanding of place value. I implore you to not teach other objectives of mathematics if their understanding of place value is not secure.
Teaching addition and subtraction, multiplication or place value concepts that are beyond their understanding is like building a house with sand as foundations; it is destined to fall down and crumble. Any new learning that they cannot make sense of will fall out of their head.
Take the time to ensure the foundations are secure so that their mathematical ‘house’ can thrive.
Note: This guide will not address the teaching of decimals and decimal places as it is a separate area of the national curriculum covered in the article on teaching decimals KS2.
Teaching place value at KS2: the theory
The theory of place value, its utility and pedagogical approaches do not change throughout the year groups.
Rather, the numbers that students are expected to master increases and the comparisons between the numbers become more sophisticated.

Unlimited primary maths tutoring with Skye, the voice-based AI maths tutor.
Built on the same principles, pedagogy and curriculum as our traditional tutoring, but with more flexibility, reach and lower cost.
Join the schools already helping hundreds of primary pupils nationwide with Skye’s one to one maths tutoring.
Watch Skye in actionUnits or ones: what’s the difference?
Some teachers may remember teaching place value (or indeed being taught place value by their teachers) and the first position being referred to as a unit.
This caused some issues when students were then looking at measurements and teachers would remind pupils not to forget the units in the answer, an instruction which was often met with a bewildered look.
As of 2014, the terminology of ‘ones’ has become far more commonplace to describe the place value assigned by the numbers 0-9.
Numbers, digits and numerals: what’s the difference?
This brings me to the next part I wish to bring to your attention (and a key part that is often missing from the conversation of place value): the difference between number, digit and numeral.
A number is a count or measurement of something that is quantifiable. We quantify the count or measurement by using numerals; numerals can be written using symbols we call digits.
There are 10 digits in our number system: 0, 1, 2, 3, 4, 5, 6, 7, 8 and 9.
Numerals can also be written using letters to create words e.g. one, five hundred etc. Teachers need to be careful with the language that they use when teaching place value as it is too easy to fall into common traps such as, ‘What number goes into the tens?’.
As ‘number’ can refer to anything that is quantifiable, we are literally asking students to place a whole number within the place value when really, we should be asking what digit.
By reinforcing that the digits are 0-9 and that only one digit can go into each place value, we reinforce the notion that there can only be one digit for each place value, a key aspect of place value theory.
Free Place Value Concertina
Download our free, step-by-step instructions for making and using a place value concertina for your KS1 or KS2 class!
Download Free Now!Best place value manipulatives
When looking at place value, going from concrete to pictorial to abstract is important. The maths manipulatives shown below should be staples of every classroom from Early Years to Year 6.
1. Dienes for place value
Dienes in base 10 and place value counters make up the most common manipulatives used for teaching this concept.
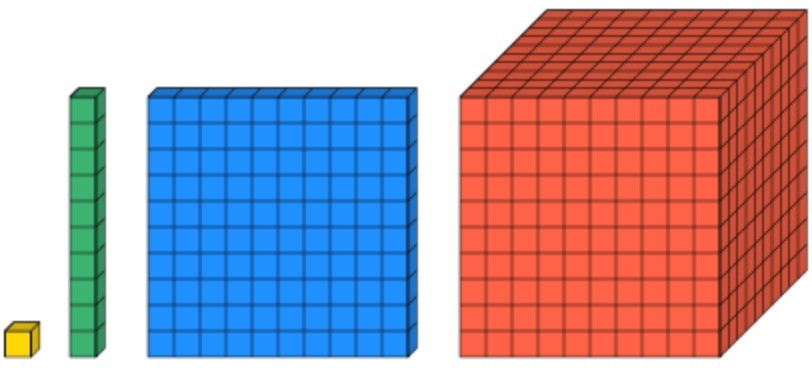
Dienes are what I would suggest working with first as there is a size and proportional element showing the difference or relationship between the values. This would be far easier for a younger learner to grasp than a different colour counter.
The downside to the dienes is that they only go to 1,000, so as soon as you are required to work with numbers in the tens of thousands, there are no dienes to support this.
It is important that before students start working in base 10,000 they are also introduced to working with counters so they can easily transition between the two resources.
A further advantage of the dienes is that it is easy to see the equality between each piece. From a young age, students can see that 10 of the ones blocks are equal to 1 of the tens blocks and so on. Understanding this equivalence is key to understanding place value and to be able to perform more complex mathematics.
2. Place value counters
Place value counters and grids, on the other hand, are less concrete in that there is no physical difference between the counters, so the conceptual understanding developed with dienes must lead into using them for understanding to be transferred.
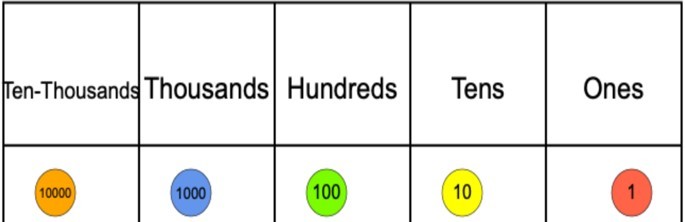
Time spent developing students’ understanding that 10 ones counters can be exchanged for 1 tens counter etc. must be prioritised before any additional work with counters can continue.
Ultimately, the end goal of all these manipulatives is for children to stop relying on them completely, moving onto using just a place value grid and then their own intuitive understanding; teachers will need to plan for this while taking individual needs into account.
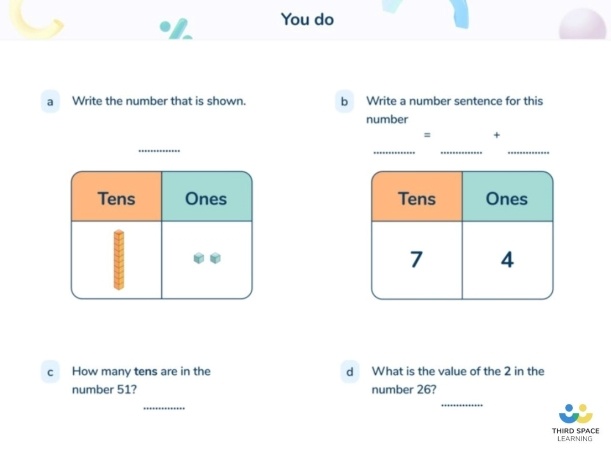
taken from Third Space Learning’s online maths intervention lessons.
Place value Year 3
In the national curriculum for maths in England, for each area of maths outlined there is both a statutory requirement and a non-statutory requirement.
Place value Year 3 statutory requirements
- Count from 0 in multiples of 4, 8, 50 and 100; find 10 or 100 more or less than a given number;
- Recognise the place value of each digit in a 3-digit number (100s, 10s, 1s);
- Compare and order numbers up to 1,000;
- Identify, represent and estimate numbers using different representations;
- Read and write numbers up to 1,000 in numerals and in words;
- Solve number problems and practical problems involving these ideas.
Place value Year 3 non-statutory notes and guidance
- Pupils now use multiples of 2, 3, 4, 5, 8, 10, 50 and 100;
- They use larger numbers to at least 1,000, applying partitioning related to place value using varied and increasingly complex problems, building on work in Year 2 (for example, 146 = 100 + 40 + 6, 146 = 130 +16);
- Using a variety of representations, including those related to measure, pupils continue to count in 1s, 10s and 100s, so that they become fluent in the order and place value of numbers to 1,000.
Place value activities and lesson ideas for Year 3 pupils
In Year 3 place value, students are expected to become familiar with numbers up to 1,000. They should explore these numbers using base 10 dienes blocks to create and recognise numbers.
Teachers should deliberately plan to create errors when modelling. For example, placing 11 ones counters into a place value chart, making that error explicit and getting the students to explain why this is not allowed. This should be the cornerstone of any modelling when it comes to place value.
Build up pupil confidence by getting them to represent two-digit numbers using dienes blocks and a place value chart. Show them how to represent 35, for example, and model this with dienes.
Note that the way you arrange the dienes can be helpful. Here the ones are arranged in a familiar pattern (5 on a dice) which will help students to see that there are indeed 5 five there without having to count each block individually.
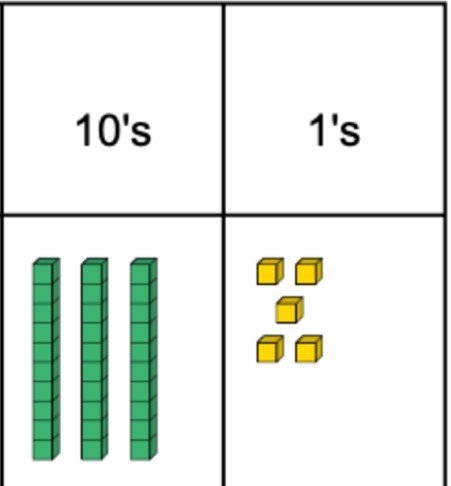
Go through many examples with pupils using the ‘I do, we do, you do’ approach to ensure that students are able to perform what it is you are asking them to do. Once you are confident that students can do two-digit numbers, repeat the process but with three-digit numbers.
It is also important that you reverse the process. Instead of only asking students to represent a number with the dienes, show dienes and ask students to explain which digit is being represented, the value of that digit and then the number that the digits represent.
For example, this could be shown on the board, with the teacher then expertly modelling their thinking aloud.
‘I have counted 9 ones cubes. That means the digit represented in this value is 9 and because it is in the ones value means that it represents the number 9. In the tens value, there are 3 blocks. This gives me the digit 3. Because it is in tens value, it represents the number 30.
So far I have the digits 3 and 9; which represent the numbers 30 and 9. Together this is 39. There are also blocks in my hundreds value. I have 4 blocks there. This would represent the digit 4. As it is in the hundreds value, it represents the number 400. I have 400, 30 and 9. Together this makes 439.’
Modelling aloud these thought processes helps aid the understanding of the students.
Once pupils are used to solving questions like the above in a whole-class setting, the work set should focus on having them try this individually. It is best to use interleaving between a question asking a pupil to show or draw dienes representing a number, and one using the dienes to work out what number they are representing.
This continuous change in thinking between each question, while leading to some challenge in the lesson, will produce more meaningful long-term learning.
Read more: 10 place value games and activities suitable for KS1 & KS2 or take a look at our collection of place value worksheets for KS1 and KS2.
Place value problem solving and reasoning Year 3
A typical year 3 place value problem to be solved would look like the following.
Which of the following sets represents the number 222? Explain why you made your choice!
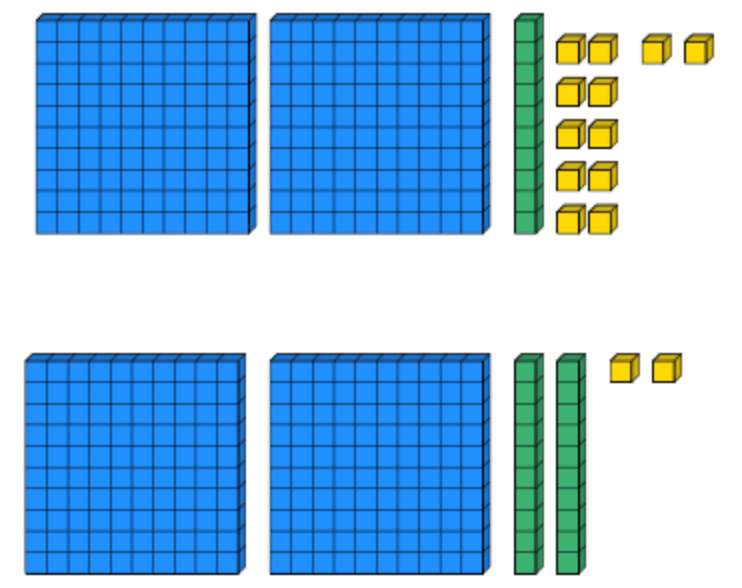
The key here is that both of these representations represent the number 222, just in different ways. The first contains 10 ones blocks which are equal to 1 tens block. This question has been specifically designed to check if pupils can recognise this equivalence.
Place value word problems in Year 3
Due to the nature of place value, it is not appropriate to have typical word problems as you would have in other areas of mathematics (e.g. the four operations, statistics and data handling etc.)
Place value Year 4
Place value Year 4 statutory requirements
- Count in multiples of 6, 7, 9, 25 and 1,000 (a times table grid can be helpful with learning multiples of 6, 7 and 9);
- Find 1,000 more or less than a given number;
- Count backwards through 0 to include negative numbers;
- Recognise the place value of each digit in a four-digit number (1,000s, 100s, 10s, and 1s);
- Order and compare numbers beyond 1,000;
- Identify, represent and estimate numbers using different representations;
- Round any number to the nearest 10, 100 or 1,000;
- Solve number and practical problems that involve all of the above and with increasingly large positive numbers;
- Read Roman numerals to 100 (I to C) and know that over time, the numeral system changed to include the concept of 0 and place value;
Place value non-statutory notes and guidance
- Using a variety of representations, including measures, pupils become fluent in the order and place value of numbers beyond 1,000, including counting in 10s and 100s, and maintaining fluency in other multiples through varied and frequent practice;
- They begin to extend their knowledge of the number system to include the decimal numbers and fractions that they have met so far;
- They connect estimation and rounding numbers to the use of measuring instruments;
- Roman numerals should be put in their historical context so pupils understand that there have been different ways to write whole numbers and that the important concepts of 0 and place value were introduced over a period of time.
Place value activities and lesson ideas for Year 4 pupils
When comparing and ordering numbers to 1,000, a typical Year 4 place value lesson may look like the example below. Note that you would have to teach the following objectives first before attempting this one.
- Find 1,000 more or less than a given number;
- Recognise the place value of each digit in a four-digit number (1,000s, 100s, 10s, and 1s).
Pupils will already be familiar with the equal sign (=) and the greater than (>) and less than sign (<). It is here I would implore you to check if your class have been taught the greater than and less than signs (e.g. through a metaphor involving crocodiles and how their tea is always the bigger number).
This does little to help pupils’ conceptual understanding of what the symbols mean. It makes far more conceptual sense that on a horizontal number line > points towards the greater numbers and < points towards the numbers that are smaller.
When comparing numbers, pupils should continue to use manipulatives, draw the numbers pictorially or write them using digits or in written form.
Students should use their knowledge of manipulatives to understand what numbers are being represented and to determine which of those numbers are either greater, less than or equal to another number.
Here we can see how this question borrows from the learning of the Year 3 place value lesson; this is chosen deliberately so the students are not grappling with too much new content straight away.
The Year 4 pupils would be expected to work out the number from the visual representation before using the correct symbol to show the relationship between the two values.
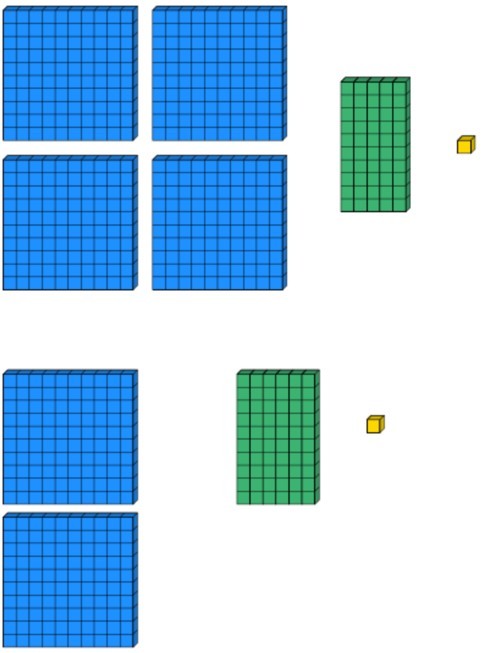
The first representation shows the number 451 and the second representation shows the value 251.
Students should place the correct symbol between the two numbers, getting 451 > 251.
Model other examples using counters and numerals with numbers up to 9,999.
When students are confident in this, use a range of place value counters, numerals (both digit and written) and mix up the variations. For example, 1,541 > 1,531.
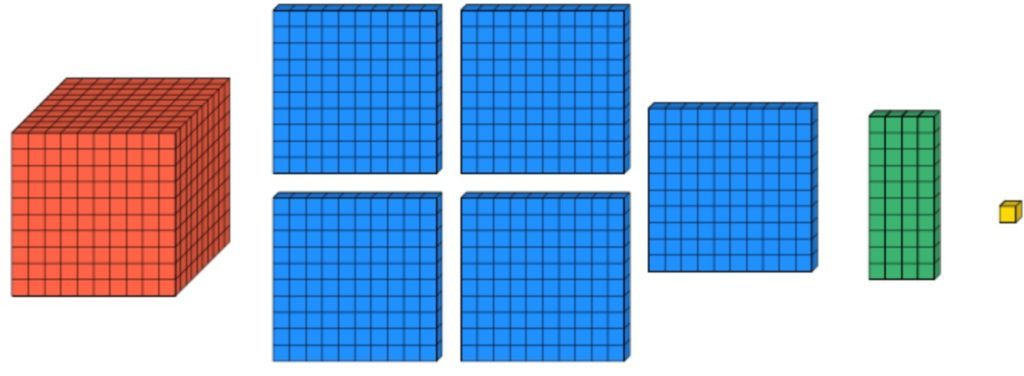

And then just use words: four thousand, nine hundred and ninety-eight = 4,998.
Place value problem solving and reasoning Year 4
A typical reasoning or problem-solving activity for place value in Year 4 would have some degree of openness about it where multiple answers could be available. This is an important mathematical idea for students to realise as this will aid their understanding of more complex maths later on.
Using the digits 1, 2, 3, 4, and 5 only once, complete the comparisons.
456_ < _73_
2_83 > 24_3
This question can provide plenty of rich mathematical discussion which would be hard to document here.
The role of the teacher should be to encourage mathematical thinking (not simply trial and improvement), while still demonstrating to the students that mistakes may well be made and that this is perfectly okay and natural. The most important way to get students thinking mathematically on this task is to reinforce that when comparing numbers, we always begin by looking at the biggest value.
Possible answer:
4561 < 4732
2583 > 2433
Place value word problems in Year 4
Due to the nature of place value, it is not appropriate to have typical word problems as you would have in other areas of mathematics (e.g. the four operations).
Place value Year 5
Place value Year 5 statutory requirements
- Read, write, order and compare numbers to at least 1,000,000 and determine the value of each digit;
- Count forwards or backwards in steps of powers of 10 for any given number up to 1,000,000;
- Interpret negative numbers in context, count forwards and backwards with positive and negative whole numbers, including through 0;
- Round any number up to 1,000,000 to the nearest 10, 100, 1,000, 10,000 and 100,000;
- Solve number problems and practical problems that involve all of the above;
- Read Roman numerals to 1,000 (M) and recognise years written in Roman numerals.
Place value Year 5 non-statutory notes and guidance
- Pupils identify the place value in large whole numbers;
- They continue to use number in context, including measurement. Pupils extend and apply their understanding of the number system to the decimal numbers and fractions that they have met so far;
- They should recognise and describe linear number sequences (for example, 3, 3 ½, 4, 4 ½ …), including those involving fractions and decimals, and find the term-to-term rule in words (for example, add ½).
Place value activities lesson ideas for Year 5
The progression from Year 4 to Year 5 place value sees many of the same objectives needing to be taught with ever-increasing numbers. This part will look at some strategies for Roman numeral teaching to ensure that they are remembered.
Teaching Roman numerals Year 5
Pupils will have first encountered Roman numerals in Year 3 in the context of clock faces and teaching time, and then in Year 4, they are expected to learn them up to 100 (C).
In Year 5, this is then extended to Roman numerals to within 1,000 (M). While the addition of Roman numerals to the 2014 curriculum is contentious, it is still a legal requirement and so must be taught.
It is imperative that by this stage, students are familiar with the following rules regarding Roman Numerals.
- Only three numerals are allowed to occur consecutively;
- There is no 0 in Roman numerals;
- When a numeral appears after a larger or equal numeral it is added e.g. VI = 5 + 1;
- If a smaller value comes before a larger value, then the smaller value is subtracted from the larger value e.g. XC = 90. This could be reinforced using consistent phrases and language such as ten away from one hundred.
Pupils will need to learn that D represents 500 and M represents 1,000. Depending on the cohort, I would suggest that these are taught over two days should curriculum time allow.
M should be tied to the idea of a millennium being 1,000 years and is a unit of time we still refer to. Children should now know the following numerals and their values.
I = 1
V = 5
X = 10
L = 50
C = 100
D = 500
M = 1000
A common activity so that pupils can remember the order of the numerals is to take each letter and create a mnemonic. Research suggests that this is an appropriate learning strategy if there is little meaning or everyday use of some content.
One that I have seen taught to my pupils is ‘I Value Xylophones Like Cows Do Milk.’
The limitation of this is that while it provides the order of the numerals, it does not provide the values. This is something to be aware of.
In terms of task design, using Roman numerals to aid with partitioning (breaking up of numbers into their place value) is a worthwhile endeavour and one that can be of considerable utility.
For example, getting students to partition CCCLXII into their Arabic counterparts of 300 + 60 + 2 and then combining those into 362 helps to reinforce place values in our number system.
Should this prove too difficult still, then breaking each numeral down into its component part should be done first e.g. 100 + 100 + 100 + 50 + 10 + 1 + 1. This will depend on the pupils’ prior attainment.
Providing manipulatives discussed in previous year groups for pupils to write as Roman numerals, or showing the Roman numerals and having pupils recreate them using manipulatives is another meaningful task.
For example, your class could be expected to write the following in Roman numerals.
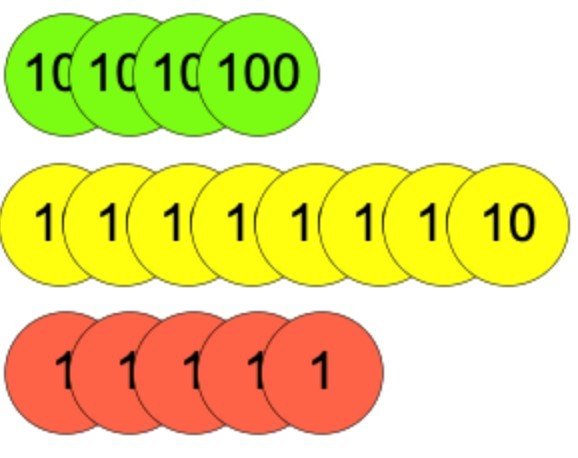
Getting pupils to find the total of each row of place value counters would be the first step of solving this, before then converting those values into Roman numerals.
- 400 = CD
- 80 = LXXX
- 5 = V
- 485 = CDLXXXV
Once students are secure in numerals up to 1,000, they should be able to apply the rules outlined at the beginning of this section to write the date in Roman numerals going forward.
This allows for constant repetition of this area of mathematics without devoting much more dedicated curriculum time to it.
Place value problem solving and reasoning Year 5
Open-ended activities and, if possible, using the four operations within Roman numerals, is a good way to assess pupils’ problem-solving abilities for Year 5 place value.
Providing an equation in Roman numerals such as CDL + CL = DC, and asking pupils how else they can create that total using the four operations and their knowledge of Roman numerals provides an adequate challenge, while also allowing children to practice arithmetic.
Place value word problems in Year 5
Due to the nature of place value, it is not appropriate to have typical word problems as you would have in other areas of mathematics (e.g. the four operations).
Read more: Teaching Place Value in Year 5 and Year 6: How To Identify and Fix The Most Common Gaps
Place value Year 6
Place value Year 6 statutory requirements
- Read, write, order and compare numbers up to 10,000,000 and determine the value of each digit;
- Round any whole number to a required degree of accuracy;
- Use negative numbers in context, and calculate intervals across 0;
- Solve number and practical problems that involve all of the above.
Place value Year 6 non-statutory notes and guidance
- Pupils use the whole number system, including saying, reading and writing numbers accurately.
Place value activities and lesson ideas for Year 6
By Year 6 place value, pupils should have developed a thorough understanding of place value and so understanding numbers to 10,000,000 should prove little challenge.
And with pupils having (hopefully) learnt the long multiplication method and begun covering long division, they should be comfortable using place value in conjunction with the four operations in a variety of situations.
The aspect of Year 6 place value that often trips children up still is negative numbers. Their journey with negative numbers begins in Year 4 place value where they count backwards through zero.
In Year 5 place value lessons they are expected to ‘Interpret negative numbers in context, count forwards and backwards with positive and negative whole numbers, including through 0’.
Once they get to Year 6, place value includes completing calculations such as -3 + 5.
Teaching negative numbers Year 6
One of the most effective methods I have come across to teach this is through the use of double-sided counters.
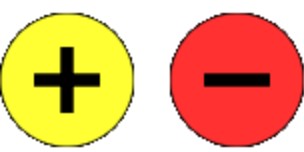
As you can see from the above, one of the counters has a negative value and the other counter has a positive value.
Consistent use of language throughout the teaching of negative numbers is crucial. They should never be referred to as minus numbers. Minus is a synonym for subtraction and should not be used to describe numbers below zero; they should only be referred to as negative numbers.
When doing this lesson, I found it most beneficial to go back to basics. I would show three positive counters and ask the class how many there are.
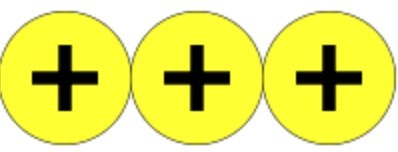
I would then ask how many I would have if I added one more counter and physically bring one more counter to the set.
Understanding the relation to zero is paramount; pupils need to be aware that when using positive numbers the larger the number, the further away from zero it is. I would then show some negative counters.
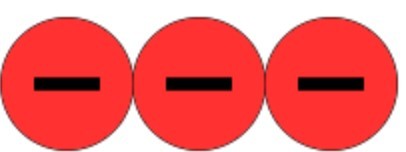
Pupils will be able to see that this represents -3. I would then ask what would happen if I added one more negative counter and show this with the counters.

Students can see that I now have -4 and can see that as I add more negative numbers the number gets further away from zero.
They are beginning to see that positive and negative are a reflection of each other. When a positive is added to a positive, it gets bigger and further away from zero and when a negative is added to a negative, it gets smaller and further away from zero.
The same would be repeated for subtraction and modelled consistently with pupils having the opportunity to try this. By the end, they will be able to see that taking a positive number away from a positive number decreases the number and gets it closer to zero, and subtracting a negative counter increases the value of the number as it makes it closer to zero.
Do not underestimate the amount of practice pupils may need to grasp that conceptual understanding!
An important place value activity: the additive inverse property
Once they are confident with that, I would present them with this on the board.
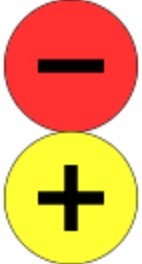
This is a good opportunity to introduce the additive inverse property to pupils. When you add a number to the same negative value e.g. 1 + (-1), you will always make zero, and this is known as a zero pair.
I would model this several times with different numbers and their corresponding counters. Websites like MathsBot are useful for explaining this property, showing how putting a positive and negative value together makes them disappear from the screen completely to show zero. I would always show them this version as it makes it easier to understand.
1 + (-1) = 0
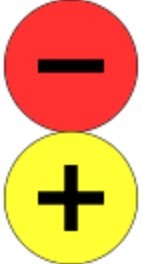
3 + (-3) = 0
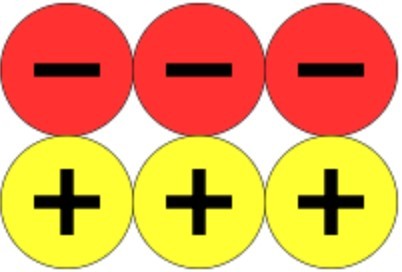
4 + (-4) = 0
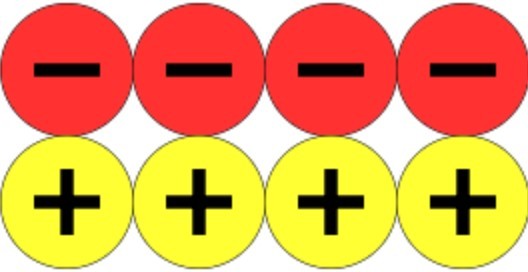
Once pupils understand this, questions such as -3 + 5 become far more accessible to all. They need to get the required counters.
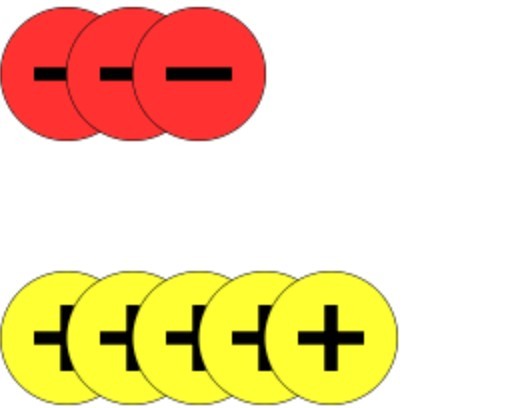
Look for any zero pairs by pairing a negative and a positive together.
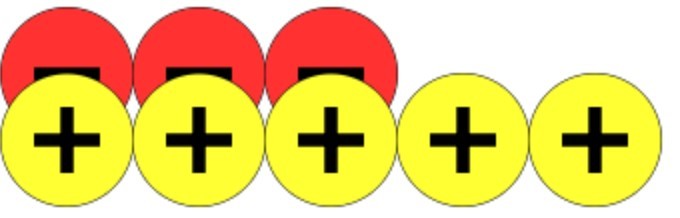
As these are worth zero, these can be removed. This leaves you with only two positive counters left, meaning that the answer must be positive two.
More examples would be completed using the ‘I do, we do, you do’ approach to guide practice before setting them off on some independent practice when you feel confident in their abilities.
Place value word problems in Year 6
Simple word problems set in real-world contexts are often used at this point, as preparation for the KS2 SATs. A common problem may look like the following.
The temperature in Moscow is 4 degrees Celsius. It drops by 7 degrees. What is the new temperature now?
To solve this, I would still encourage using double-sided counters. I would get four positive counters to demonstrate the initial temperature.
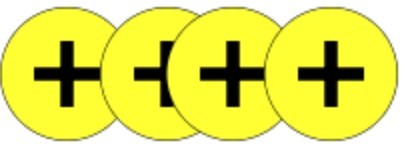
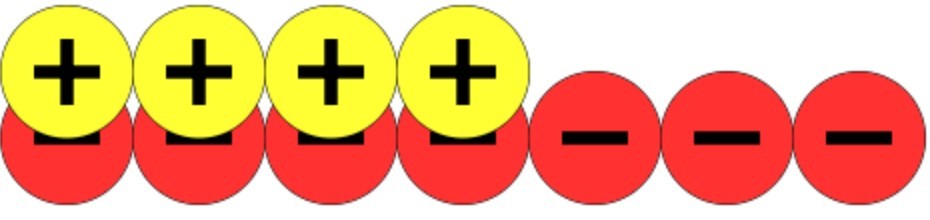
Seven negative numbers demonstrate the drop in temperature.

Find any zero pairs by matching each positive counter to a negative counter.
Remove the zero pairs and then look at what is left over.
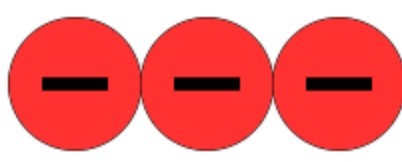
In this case, it would be negative 3.
Place value problem solving and reasoning Year 6
When counting below zero, it is important that we count zero as a step. A common reasoning problem to demonstrate this would be the following.
A car park has 15 floors above ground and 15 floors below ground.
James says there are 30 floors altogether.
Patty says there are 31 floors altogether.
Who is correct?
To solve this question, a number line is best used so that students can see that you are jumping back 31 floors as you would have to count zero as a floor.

I would also encourage pupils to bridge from 15 to 0 and then count backwards from ones to negative 15 to emphasise this point.
Hopefully, this has given you a good idea of how to get started teaching place value to Key Stage 2 pupils once the autumn term starts. Place value is one of the most fundamental concepts in maths, so making sure your pupils have a solid grasp on it really is the best way of getting the maths year started off right!
Looking to get ahead on other KS2 maths topics?
We have the lowdown from expert primary teachers on all the trickiest KS2 maths concepts to teach, including teaching times tables, telling the time, as well as the long division method and the long multiplication method.
DO YOU HAVE STUDENTS WHO NEED MORE SUPPORT IN MATHS?
Skye – our AI maths tutor built by teachers – gives students personalised one-to-one lessons that address learning gaps and build confidence.
Since 2013 we’ve taught over 2 million hours of maths lessons to more than 170,000 students to help them become fluent, able mathematicians.
Explore our AI maths tutoring or find out about a primary school maths tutor for your school.