How To Teach The Formal Long Division Method At KS2 Step By Step So Children Love It!

The formal long division method at KS2 often takes time to teach to both Year 5 and Year 6 and can be difficult for pupils to fully understand. It doesn’t have to if you have the right long division teaching strategy in place.

In this blog, Sophie Bee (@_MissieBee) explains the long division method her Year 6 pupils now follow, how to teach long division with ease this way – and even better, how to ensure your KS2 pupils start to love their new long division technique. Look out for the free long division worksheets too. 

Long division: long and divisive, right? Wrong!

Long division is probably one of my favourite things to teach Year 6 in maths (I know, I know – but bear with me).

When children watch you do it, they think it looks complicated, difficult, and unnecessary, and it almost instantly turns them off – until they realise how systematic and logical it is.

See also: Teaching Division KS2: A Guide For Primary School Teachers From Year 3 To Year 6

What is the long division?

Long division is a method for dividing one large multi digit number into another large multi digit number.

In Year 5 and Year 6 at primary school, long division usually means dividing a number that is at least three digits by one that is two digits or more, often leaving a remainder, and sometimes with the need to provide an answer to decimal places or as a fraction.

The best long division method builds on children’s understanding of the bus stop method of short division as preparation for dividing by large numbers.

As well as recognising the division symbol, children should understand terms like the dividend and the divisor before they tackle long division at KS2.

• The dividend is the number you are dividing (the number inside the ‘bus stop’).
• The divisor is the number you are dividing by.
• The quotient is the amount each divisor receives i.e. the answer in most cases.

If you feel you need a brush up on all the precursor stages to long division, then this article for teachers and parents on division for children is a great start.

What is the long division method?

The formal long division method is a step-by-step method that supports children to understand both conceptually and practically how to divide one three-digit-number by a two or three-digit number.

Unlike chunking, the long division method is set out in a similar way to short division or bus stop method of division, but uses a memorable process to get to the answer. First you divide, then you multiply, then you subtract, and then you bring the next digit down. This process is repeated till you have reached a solution.

1. Divide
2. Multiply
3. Subtract
4. And bring the next digit down

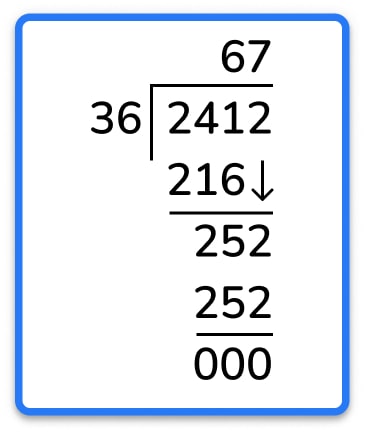
If you want to know how to teach this long division method at KS2 read on.

Long division plays an important role in SATs

We all know that the arithmetic paper is the one in which we expect the children to score the highest marks, and often, those crucial marks are lost because of inaccuracies in children’s answers.

In all four of the SATs arithmetic papers that have been released so far under the new curriculum, there have been 2 ‘long division’ (dividing by a 2-digit number) questions. 

It is therefore crucial that children are fluent in division and confident with the accuracy of their answers, and this means finding the right KS2 long division method for your class.

How to do long division method according to the national curriculum

According to the national curriculum, when teaching division to Year 6 children should know how to:

“Divide numbers up to 4 digits by a two-digit whole number using the formal written method of long division, and interpret remainders as whole number remainders, fractions, or by rounding, as appropriate for the context”.

The Mathematics Appendix 1 includes examples of formal written methods for addition, subtraction, multiplication and division. This “sets out some examples of formal written methods for all four operations to illustrate the range of methods that could be taught”, as shown below for long division. (Note that it also says, “For division, some pupils may include a subtraction symbol when subtracting multiples of the divisor”.)

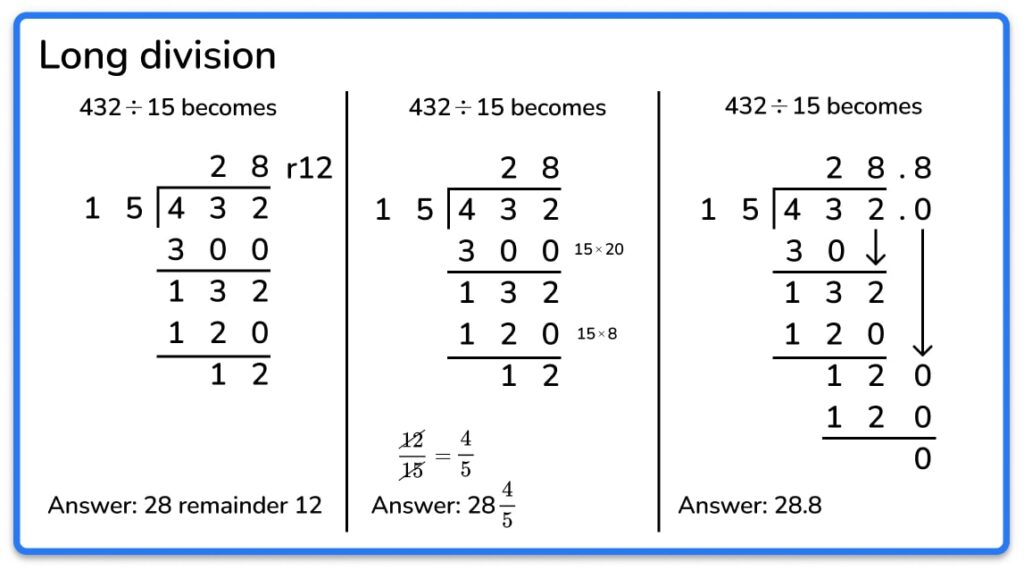
Long division chunking method

The chunking method for long division with two-digit numbers is set out in the first two columns below; it encourages children to think about the relationship between multiplication and division by estimating first how many times the divisor (the number outside the ‘bus stop’) is likely to go into the dividend (the number inside the bus stop).

Long division formal method

The long division method in the third column is my favourite and the one I recommend we should all be teaching at KS2 by following the steps below!

“Your favourite and best long division method looks too hard for my Key Stage 2 children!” I hear you shout!

I admit, when I first started teaching Year 6, I shied away from this long division method for a long time.

I’d never understood it properly, yet always considered myself a competent mathematician, so didn’t really understand the need for it.

It wasn’t until I sat down and decided to teach myself the method that I realised how systematic it was, and how it really embedded what was happening in each step of the division process – something that would be really useful both for those who struggle with mathematical concepts and for those working with decimal points and larger numbers.

Why you should teach the formal long division method at KS2

A short personal story to show you that this long division method can work is that during Year 6 SATs a few years ago, I was very conscious of one of my ‘boundary’ children – you know the ones – who really struggled with confidence and general understanding in maths.

I took a sneak peek at them completing a long division question in the Year 6 arithmetic test and watched them methodically work their way through it to achieve the correct answer. This was someone who didn’t know their times tables at the start of the year, and I could’ve burst with pride! It was a case of long division made easy at last for this primary pupil, all thanks to the long division method explained below!

But doesn’t long division take too…well…long?

Okay, so the name of the method doesn’t really help in selling itself, but once you’re fluent, it should take the same amount of time (if not less) than ‘short division’. See the long division examples below, dividing 45,041 by 73. First, we show the short division method and then the long division method.

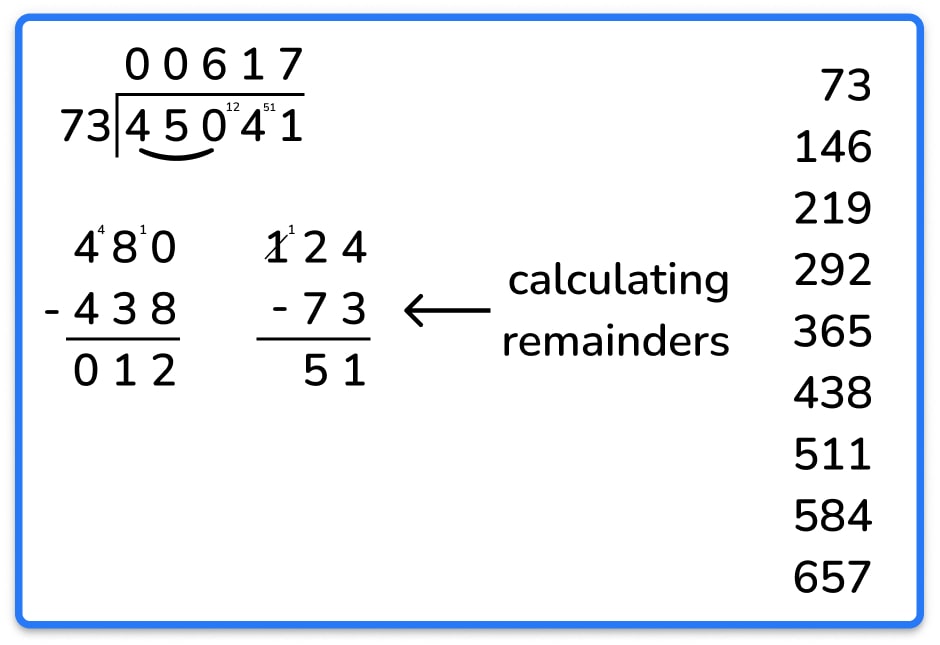
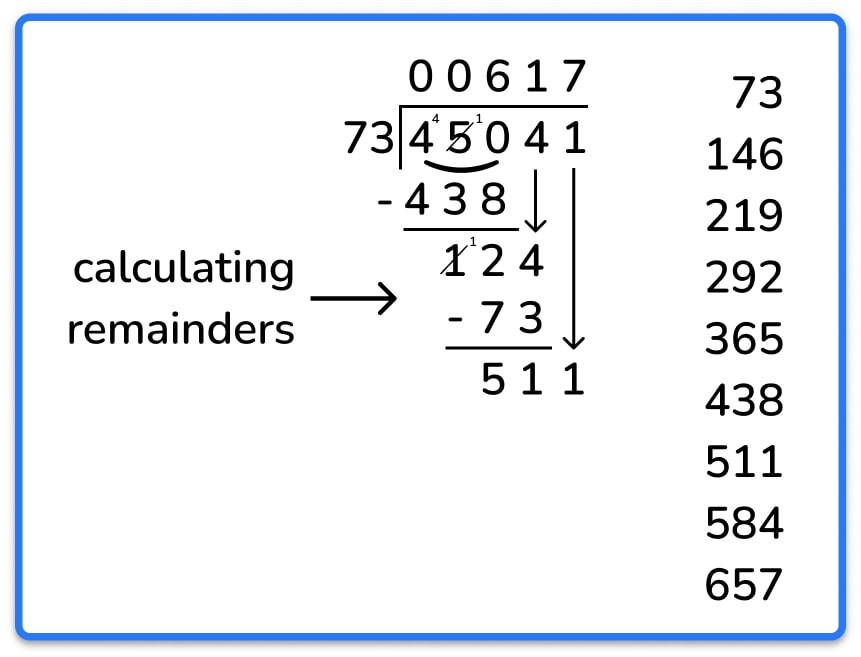
With short division, children still need to work out the remainders.

Many will need to do this via written subtraction anyway, and even if they can calculate them mentally, we all know how many mistakes are made by overconfident children when working at speed – especially when they refuse to write their workings-out!

If anything, the long division method took less time as I didn’t have to repeat myself by writing out the numbers again elsewhere on the page when calculating the remainders.

How to teach the formal long division method at KS2

Fear not! This is my tried and tested KS2 long division method when teaching Year 5 or Year 6.

On average, it would take me around three days, but as we all know, this completely depends on the cohort, so I’ve broken the process down into ‘steps’ instead to be spread across as many lessons as needed. Warning: multiplication tables will be required! 

What are the steps for teaching long division method?

In a nutshell, this is what you’re going to be teaching your pupils at KS2:

1. Recap and explain the short division method
2. Divide
3. Multiply
4. Subtract
5. And bring the next digit down

Here it is broken down

KS2 long division method: step 1

Recap short division, ensuring children can talk through the process. Do they understand what’s happening at each step? For example, you could ask:

• What is the divisor?
• Why is it important to know multiples of the divisor?
• What is a remainder?
• How have you calculated the remainder?
• What happens if you get a remainder at the end of the question?
• How can you check your calculation is correct?

Once children are confident with short division, they can move onto long division.

KS2 long division method: step 2

Dividing by 3 isn’t so scary, but dividing by 97 (as in 2018’s paper) is much more intimidating!

I’ll always start this lesson by asking children to list the first nine multiples of a ‘difficult’ number (such as 86) and watch them groan and do lots of column addition or counting on fingers or something else equally as inefficient.

Of course, there are occasionally those who know their multiplication and division facts and can whizz through these – I know a few children who would quickly list multiples of 97 by adding 100 and subtracting 3 each time, but until we have a class full of children that can do that without prompting, this method will be worth it!

I then show them how to do it by partitioning and it’s sometimes one of those moments where if a cartoon lightbulb could appear above their heads, it would (cue a chorus of “Ohhhhhh yeahhhhhh!”s).

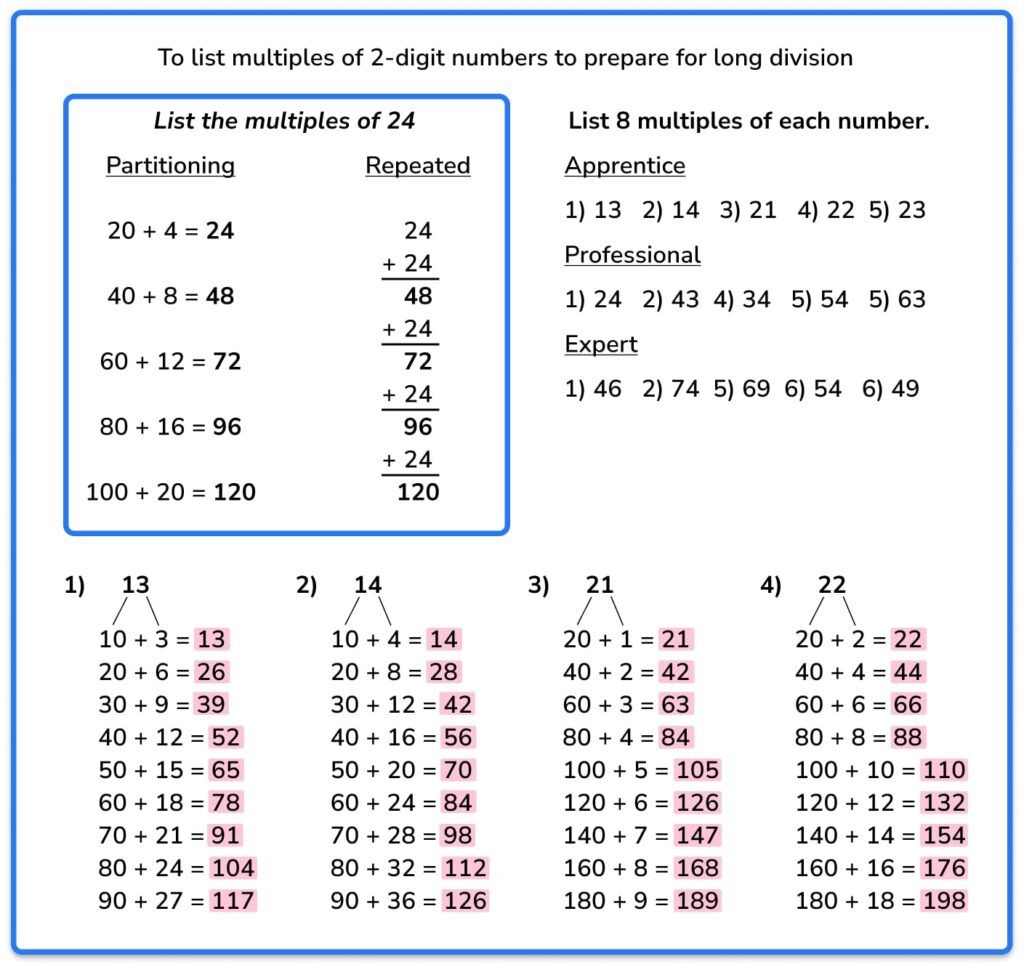
The first time I did this, it was one of those lessons which on the face of it looked intensely boring, but my Year 6 children got so carried away with their partitioning for long division that they even asked to stay into their lunchtime to finish the questions!

This just proves that engagement in lessons isn’t created from bells and whistles, but listing multiples in preparation for long division – you heard it here first!

I ask the children to list nine multiples every time – asking them why you would only need nine multiples for any long division question is a good way of obtaining their understanding of the division process. Obviously, as they gain confidence in the method, they only need to list as many as necessary.

KS2 long division method: step 3

This is where I bring in the good old ‘me, we, you’ process.

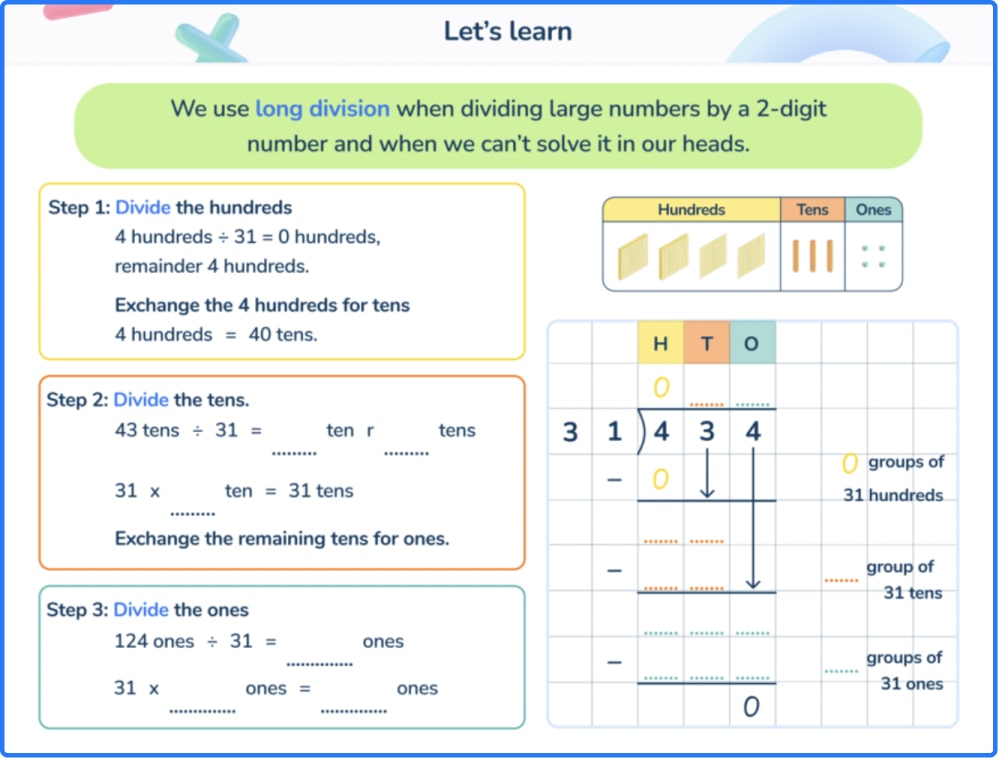
Firstly, I show them a completed modelled example:

Then, I complete the division myself (next to the modelled long division example) to show them how I achieved it, always talking through each step as I go. This is usually when you get the “What?”, “Miss, I don’t get it”, or, “That’s impossible” comments; it doesn’t take much to change their minds! Remember to work slowly through from the first digital of the dividend. 

Explaining this formal long division method as you go is very important to cement understanding among all pupils.

It’s important to explain the steps broken down: to divide, multiply, subtract, and then bring the next number down.

I encourage the children to write the four symbols down on their page to remind themselves of the steps. They should have a solid understanding of these steps as, apart from the last one, they are the same as the short division process. The long division method is:

• Divide: divide the dividend by the divisor – what is the answer without a remainder (use the list of multiples to help you).

• Multiply: multiply the answer to your previous division by the divisor to reach the multiple needed to calculate the remainder (use the list of multiples).

• Subtract: subtract the multiple from the original number to calculate the remainder.

• Bring the next digit down: this replaces the ‘write the remainder just before the next number’ step in short division.

Long division method step by step using an exemplar question

This method is far more coherently explained in the context of a specific long division question. Sometimes it’s appropriate to apply it to a division by a one digit number, to show how ‘long division’ is just a different way of setting out what they know as ‘short division’, but otherwise you can go straight into dividing by 2-digit number.

Let’s take the long division example, 13,032 ÷ 24, to model the steps of long division (assuming we’ve already listed the multiples as in the modelled example in step 3); this multiplication step is important.

1: Divide: 130 hundreds ÷ 24 → five (I can see by looking through my list of multiples that 130 would be placed between 120, the 5th multiple, and 144, the 6th multiple). 5 is written in the hundreds column as the first digit of the quotient (answer).

Note: as we’re working digit by digit from left to right, we can see that 1 ten-thousand (the first digit) can’t be divided by 24, therefore a 0 is placed in the ten-thousands answer column; this is exchanged for 10 thousands and we have 13 thousands ÷ 24 but this cannot be done, therefore another 0 is placed in the answer line for this column. We are now working with 130 hundreds (the first three digits combined) which has ensured that all the place values are correctly aligned.

2: Multiply: 5 x 24 is 120 (I should know this from the answer to the previous step, but I can also count down my list of multiples to find the 5th multiple of 24). This is the number we need to work out the remainder to our first division (130 hundreds ÷ 24).

3: Subtract: 130 – 120 = 10, so this is the remainder to the first division (130 ÷ 24). This needs to be included in our next step

4: Bring the next digit of the dividend down: bringing the 3 down makes my new number 103 tens. I’ll then repeat the process again

5: Divide: 103 tens ÷ 24 → four (I can see by looking through my list of multiples that 103 would be placed between 96, the 4th multiple, and 120, the 5th multiple). I write 4 in the tens column of my answer.

6: Multiply: 4 x 24 is 96 (I should know this from the answer to the previous step, but I can also count down my list of multiples to find the 4th multiple of 24). This is the number we need to work out the remainder from the second division (103 tens ÷ 24)

7: Subtract: 103 – 96 = 7, so this is the remainder to the second division (103 tens ÷ 24). This needs to be included in our next step.

8: Bring the next digit down: bringing the final digit down creates my final number to work with: 72.

9: Divide: 72 ÷ 24 = 3. This is written in the ones column of our answer.

10: Multiply: 3 x 24 = 72.

11: Subtract: 72 – 72 = 0. There is no remainder, so we know that the divisor must fit into the original number exactly. So our final answer is 12,032 divided by 24 is 543.

How you can get your class to check their own work

Of course, like in any activity the children do, it’s important to encourage them to check their own work.

They can do this by multiplying their answer by the divisor to see if the original number is produced. In this case, 543 x 24 = 13,032, so we know that we are correct.

If they don’t get the original number as their answer, I’ve found that the most common mistake the children make is either listing the multiples incorrectly or misaligning the place values (meaning they may have calculated one of the steps with the wrong numbers).

Numerous pupils making this latter mistake might indicate that they need to review the fundamentals of place value at KS2.

So, now you’ve taught it, but of course, you won’t yet be confident they’ve learnt it, so the final stage in consolidating long division is practising it. 

Long division method examples

If you need more long division examples, then take a look at our blog.

Here are two long division examples laid out for you:

Example 1: 288 ÷ 12 = 24

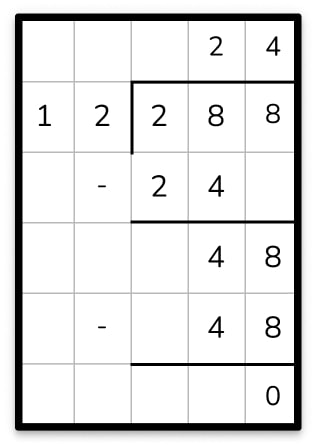
Example 2: 384 ÷ 12 = 32

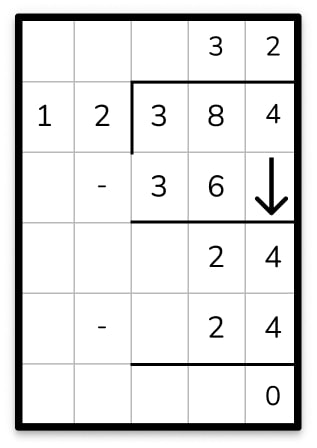
Long division method questions

Do loads of long division questions together on whiteboards and slowly take away the help. Then, when the children are ready, they can work independently.

Build up their complexity as you go; below are just six of the questions from the worksheet above, ordered in terms of difficulty to give you a general idea.

1. 2,574 ÷ 11 = ?
2. 1,476 ÷ 12 = ?
3. 4,096 ÷ 16 = ?
4. 4,488 ÷ 17 = ?
5. 13,528 ÷ 38 = ?
6. 18,473 ÷ 49 = ?

For the rest, download the free worksheets!

In my classroom, this works as a ‘peeling away’ process, which often looks like this: input to the whole class for 5 minutes – 2 or 3 children set off to work independently; input to the rest of the class for a further 5 minutes – another few children set off to work independently; input to the rest of the class for a further 5 minutes – another group of children set off to work independently.

I’m then left with those requiring the most support in long division, with whom I stay whilst my TA circulates the class, or with whom I ask my TA to stay whilst I circulate the class.

Don’t forget to download and use the free long division worksheets

Long division reasoning questions

Once children are confident with their long division method, reasoning activities can then be introduced, such as long division with missing digits, or ‘spot the mistake/s’, moving on ultimately to worded long division problems. 

Download the free Third Space Learning All Kinds of Word Problems in Division for Year 3 to Year 6.

Of course, ultimately, if you don’t feel confident with this long division method, it will never translate effectively to the children; as with anything in teaching, it must work for you and your class.

However, knowing that this is often a topic hotly debated on Edu-Twitter and Edu-Facebook, I hope I’ve converted some people to the long-division-loving side!

Happy dividing!

Here’s what the teaching community had to say on Twitter…