How To Teach Division KS2: Maths Bootcamp [7]
Want to know how to teach division for KS2 Maths pupils? You’ve found the right place!
This post is part of our interventions bootcamp series: designed to support Year 5 and 6 teachers and SATS booster group leaders to achieve age related expectations with pupils who need that extra intervention.
This bootcamp post looks at the final of the four operations, division.
Each post in the series will help school leaders, maths coordinators and upper Key Stage 2 teachers diagnose where pupils are struggling with ‘the nuts and bolts’ of that area of mathematics from the national curriculum.
We then track back to different stages of understanding and offer strategies that can be used with whole classes, booster groups or alongside one to one interventions, such as those provided by Third Space Learning.
Each post follows a similar structure:
1. First, you’ll diagnose where pupils are struggling with ‘the nuts and bolts’ of that area of mathematics from the national curriculum.
2. Next, you’ll track back to the different stages of understanding and examine what the misconception might be in detail.
3. Finally, we’ll give you strategies that can be used with whole classes, booster groups or alongside one to one interventions.
The ‘How To Teach KS2 Maths Interventions Bootcamp’ series
How To Teach Place Value Year 5 and Year 6
How To Teach Multiplication KS2
How to teach division KS2
In this post on division, we help you solve problems such as:
- Why don’t pupils use their multiplication tables to help?
- Pupils are getting completely mixed up with written division. They don’t put things in the right place and miss things out.
Maths Intervention Pack Multiplication and Division
A series of intervention lessons for pupils from Year 2 to Year 6 to help their understanding of understanding of multiplication and division.
Download Free Now!DIAGNOSIS: what are pupils key misconceptions in multiplication?
From the below pupils, find the best fit for those you are looking at. Then use this to guide where in the post to read for support:
Siobhan uses her knowledge of multiplication well in maximising her mental strategies for division. She is also fairly proficient at short division. She is beginning to develop her understanding of the long division method but needs more support to make this final transition. Stage: SECURING.
Sophie knows some times tables as facts, but frequently uses her fingers to work out others. She often gets mixed up between 3s & 4s and 7s & 8s. She prefers to do things in her head or with an array rather than attempt a written method. When using arrays, she usually draws and calculates correctly but it takes her a significant amount of time. As of yet, she is not clear on how multiplication is the inverse of division. Her place value is not secure. Stage: EMERGING.
Harrison enjoys using his range of recall to help him efficiently calculate 2 digit by 1 digit division calculations in his head. He can use the short division written method but doesn’t conceptually understand it (he just ‘does it’). He needs a clearer answer to the question: ‘what is division?’ as his current misunderstandings lead to some errors with digit positional value (seeing a ten thousand as a thousand) when calculating. When looking at long division, Harrison struggles significantly. Stage: DEVELOPING.
Yasir. When faced with any division calculation, Yasir will draw using an array. He often makes mistakes when doing so, particularly not drawing the right amount or mixing the method with multiplication. He knows some number facts but really struggles with recall. He doesn’t use the few he knows to help him in multiplication or division contexts.
Stage: PRE-BOOSTER.
Yasir’s needs are beyond the scope of a booster group or this post. He needs specifically targeted one to one support, such as that provided by Third Space Learning, to catch him up to a point where booster intervention could be considered.
Misconceptions and strategies for ‘Emerging’ in division
Sophie needs to understand the inverse relationship between multiplication and division. To do this, she needs it to be modelled using her preferred method, arrays. She has become ‘stuck’ at this stage.

To begin, show Sophie a calculation such as 7 x 6. Using counters, place them in 7 groups of 6 on a plain piece of paper. Then ask Sophie and other pupils in this booster what they see.
Model how we also have 6 x 7 as well as 7 x 6 by turning the paper through 90 degrees. Discuss how when we look at multiplication we can use either multiplication table to help us.
Move on to a couple of calculations such as 8 x 6 or 7 x 12 to see if pupils are able to calculate these mentally by using the commutative property of multiplication as explained above. This will begin the process of ‘weaning them off’ arrays.
Once pupils can choose their better recall based times tables to help them without arrays, they are ready to be introduced to the inverse.
To fully understand that they can use multiplication to help them calculate division, pupils need experience with division as grouping rather than sharing, as it is only when grouping that multiplication is the inverse of division. You can read on blog on how to teach division for more information about grouping and sharing in division.
Show your pupils the same array as previously made with counters (7 x 6 = 42). Ask them again what they see. They will likely say 7 groups of 6 counters and also 6 groups of 7 counters. Discuss that we can use grouping, as we have here for multiplication.
Then write this calculation: 42 ÷ 7 = 6. Model that through our multiplication calculation we already have 42 split into groups. Our current calculation can be read as 42 grouped into sevens, with 6 in each group. Discuss how we could also see this as 42 grouped into sixes, with 7 in each group.
Carry out further calculations with counters until they are secure with the concept. Do not use pictorial representations for any of the above as this will give them a strategy to further cling to arrays. We want to move them swiftly on.
Now that pupils like Sophie have a better understanding of the inverse property of multiplication to division and can use it to support them calculate simple division calculations, they are ready to join pupils like Harrison and be re-introduced to short division.
Misconceptions and strategies for ‘Developing’ in division
Stage 1 – Building understanding
The first stage is to lay out 84 ÷ 3 in the formal written way. Pupils like Harrison will likely do this in their head so explain that this is fine for them to do, if they are accurate. You should emphasise that we are exploring the method in a simple form so they can apply it to more extensive division calculations.
If they continue to be less engaged because they can’t see ‘the point’ in what they are being shown, give them a 2 digit number by 4 digit number and offer to race them. You can use the written method and they can use mental strategies, they will soon come around.
Using base 10 equipment, get the group to build 84. Remind pupils that division is about grouping and in this question, specifically how many groups of 3 can be made from 84. Then ask them to find this out.
At this point, watch for pupils who are a step ahead of others and exchange without prompting. Then use them to assist in your modelled explanation afterwards, which should sound something like this: “We can make 1 group of three out of our 4 ones. But then I can’t split up 1 ten into a group of 3 so I will exchange it.”
Begin to go through the motions of exchanging and finding individual groups of 3. Watch for any pupils who are already protesting that there is a faster way. If none come, exaggerate your “annoyance” at how long this is taking to help them understand there must be a faster way.
Let pupils explore and nudge them if necessary by asking ‘Is there another way of grouping these into threes?’ and finally ‘can we group into a larger amount of group of threes?” The aim is to help pupils build their depth of understanding. So following any discussion, show pupils that if we group our tens into 3, we have 3 tens (30 ones) in each of our groups. Then, because we know that ten groups of 3 are in our three times table, we know we can group them like so. Pupils should see that this is quicker than grouping everything into individual groups of 3.
Discuss with pupils how we are still left with 2 tens after grouping 8 tens into groups of 3. Explain that this is as far as they can go with grouping into 10 lots and so we should now write ‘2’ on our written method layout.
Model how the remaining two tens will need to be split into individual groups of three and exchanged. Make a point of how we write these 2 tens in our written method, similar to what they have previously down with subtraction.
Explain that doing the actual exchange with physical objects takes a while and there is a quicker way we will learn later (many pupils will see they can use multiplication tables). Pupils should then see there are 8 groups of three left. This is then written next to the twenty groups of 3 to make 28 groups of 3.

Give pupils time to try these themselves, moving towards the use of place value counters rather than base ten. They will then be able to apply their growing understanding to hundreds, thousands and beyond.
Stage 2 – Developing the written method
They are now ready to attempt 3 or 4 digits divided by 1 digit calculations using short division. Using place value counters to support them where necessary the goal should be to move towards the purely abstract short division method whilst retaining their understanding.
First, get pupils to write the short written method layout for 312 ÷ 6. Now is the time to learn a quicker way, rather than having to use counters to do lots of exchanging physically.
Show them how we do not have enough hundreds (three) to make them into groups of 6. So we need to exchange. Model how we put the 3 when it is exchanged to make 31 tens. Note how we haven’t had to ‘do’ anything as the three was still there before (which can be referred back to when then looking at moving into long division).
Explain how we can split 31 tens into 5 groups of 6 by using our times tables, leaving 1 ten remaining. Model writing the 5 groups of ten in the method. Ask what we should do with the one remaining ten. Then exchange it next to the ones, leaving 12 ones. Ask again, what we should do next, with the answer being how many groups can we make from our 12 ones (2 groups of 6). This gives us 52.

Give pupils lots of practice as they need to be secure with the exchanging, initially with place value counters as support before removing them as individual pupils stop using them. They are then ready to be introduced alongside pupils like Siobhan, who need to become secure with the long division method.
Misconceptions and strategies for ‘Securing’ in division
There is no easy way around it, the long division method is hard for pupils to fully understand. It requires them to build on their prior understanding of place value, division and multiplication, all in an abstract form. However, to begin with, we can support them by using place value counters which will significantly aid their understanding.
Give pupils a 4-digit number to be divided by a 2-digit number. Take pupils through, while writing and using place value counters, one step at a time.
First, everyone writes 3834 ÷ 27 in the formal written method. Remind pupils who were present of when we had 3 hundreds in a previous example of how we re-wrote it into tens as there weren’t enough hundreds to make groups. Explain that this method simplifies all the exchanging and avoids situations like that. Note how other than that, the process is the same as the short division they already know.
Read more: What Is Bus Stop Method: Explained For Primary School
Now explain that we do not have enough thousands (3) to make groups of 27 thousand. So we then look at the 3 thousands as hundreds, making 38 hundreds together. Mention how this is like the exchanging we have done previously. Do we have enough hundreds to make groups of 27 hundreds from them? Yes, 1.
Write the 1 in the method answer position and ask pupils how many hundreds we have left by asking them to take 27 hundreds (the one group away). Model this with the place value counters.
Establish that the 11 hundreds left are the same as 1 thousand and 1 hundred and model writing these 11 in the correct position under the one group of 27 in our written method. Again, explain this is the equivalent of our exchanging (model pushing our 11 hundreds to the tens counters because there aren’t enough to make groups of 27 hundreds).
Now model bringing down the 3 tens (the same as pushing those place value counters together) and writing it next to our remaining 11 hundreds to make 113 tens.
Using the place value counters to support (exchanging the hundreds and thousand if necessary into tens), ask pupils how many groups of 27 tens can they make. After this initial example, pupils shouldn’t need to exchange with the counters, they should be able to ‘see’ that the 1130 represented by the counters can be seen as 113 tens and then find how many 27’s go into it.
Establish that it is okay to use jottings to help them do this to find that you can make 4 groups of 27. Everyone writes the 4 in the answer position of the written method.
As before, write how many are left underneath and bring down the ones column to make 5 tens and 4 ones (54 ones). Pupils should be able to quickly see that doubling 27 makes 54, so 2 groups can be made. Write this to complete the calculation.
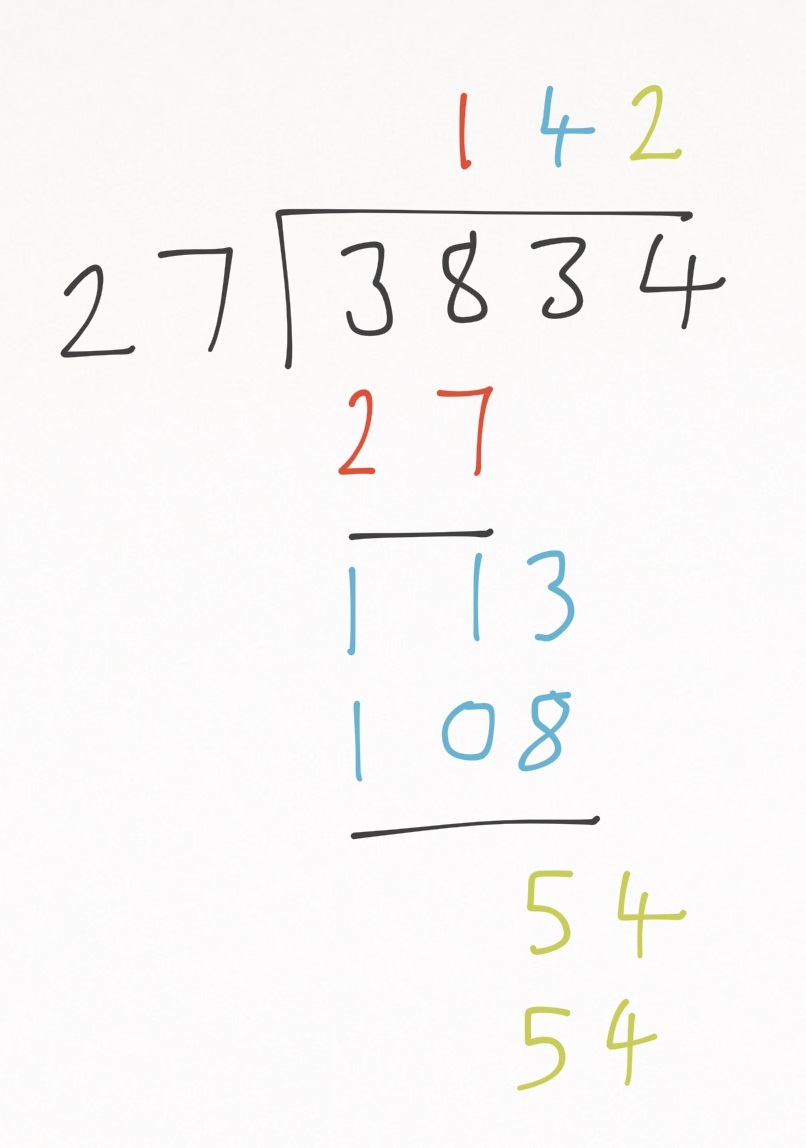
From here, it is purely a case of developing understanding and fluency, removing the place value counters as that happens. You can find more ideas and insights on long division lesson planning and teaching, long division examples and long division questions on our blog.
Don’t forget to download your FREE division resources:
Division Questions That Will Test Your Primary School Pupils
Free Division Worksheets For Primary School: Year 2 to Year 6
Further reading:
What Is Division With Remainders? Explained For Primary School
DO YOU HAVE STUDENTS WHO NEED MORE SUPPORT IN MATHS?
Every week Third Space Learning’s maths specialist tutors support thousands of students across hundreds of schools with weekly online maths tuition designed to plug gaps and boost progress.
Since 2013 these personalised one to one lessons have helped over 150,000 primary and secondary students become more confident, able mathematicians.
Learn about the scaffolded lesson content or request a personalised quote for your school to speak to us about your school’s needs and how we can help.