Partitioning Explained For Primary School

Partitioning is a phrase that even the youngest primary school child will probably know. Here we show you how Year 2 children are taught this skill to help them break down any number into its component parts. We also show how this skill is related to other areas of maths.

This article is part of our series designed for teachers to inform mathematical subject knowledge, and for parents to help support children with home learning. More free home learning resources are also available on this website.

What is partitioning?

Partitioning is a way of splitting numbers into smaller parts to make them easier to work with. Partitioning links closely to place value: a child will be taught to recognise that the number 54 represents 5 tens and 4 ones, which shows how the number can be partitioned into 50 and 4. By moving tens and ones between the two parts, the number can be partitioned in many other ways:

When shown a number (up to 7+ digits by Year 6), children should be able to partition them independently to show good understanding of place value. For example, 5,202,086 = 5,000,000 + 200,000 + 2,000 + 80 + 6.

See also: Division Worksheets

When will my child learn about partitioning in primary school?

Partitioning is taught very early on in pupils’ maths lessons, but it is first mentioned in the national curriculum as non-statutory guidance for Year 2:

Pupils should partition numbers in different ways (for example, 23 = 20 + 3 and 23 = 10 + 13) to support subtraction. They become fluent and apply their knowledge of numbers to reason with, discuss and solve problems that emphasise the value of each digit in two-digit numbers. They begin to understand zero as a place holder.

In Year 3, the non-statutory guidance advises that children use larger numbers to at least 1000, applying partitioning related to place value using varied and increasingly complex problems, building on work in year 2 (for example, 146 = 100 + 40 and 6, 146 = 130 + 16).

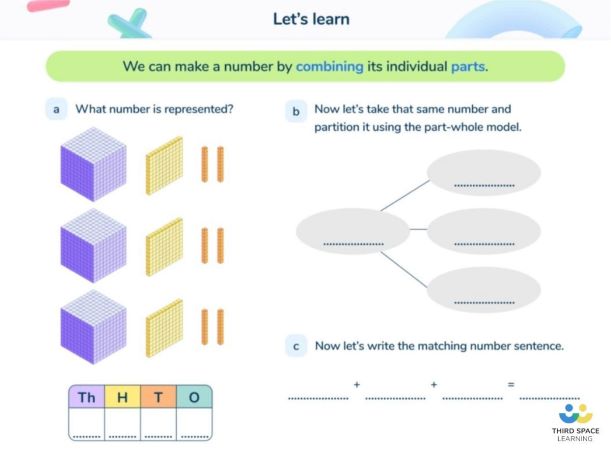
How does partitioning relate to other areas of maths?

Children will use partitioning in many other areas of maths:

• Introducing column addition: 56 + 78 may be first calculated as (50 + 70) + (6 + 8)
• Introducing column subtraction: 56 – 22 may be first calculated as (50 – 20) + (6 – 2)
• Understanding exchanging in column subtraction: 32 – 18 may be first calculated as (30 – 10) + (2 – 8) until children realise that they can’t subtract 8 from 2 without reaching a minus number. Partitioning is important here in understanding why exchanging works. 32 can be partitioned into 20 + 12, so this subtraction can be recalculated as (20 – 10) + (12 – 8)
• Introducing multiplication: 34 x 6 may be first calculated as (30 x 6) + (4 x 6)
• Introducing division methods with multi-digit divisors, including long division, short division and bus stop method, which require pupils to use multiples of the divisor and to calculate division with remainders

See also: Division Questions

Wondering about how to explain other key maths vocabulary to children? Check out our Primary Maths Dictionary, or try these other terms:

• What Is Division?
• What Is BODMAS (and BIDMAS)?
• Division For Kids: How To Teach Short Division (Bus Stop Method) And Long Division To Children
• How To Teach Division KS2: Maths Bootcamp [7]
• What We’ve Learnt From Teaching Our Long Division Lesson 2,968 Times

Practice questions

1) Write the missing numbers.
361 = ___ + 60 + 1 300
945 = 900 + __ + 5     40

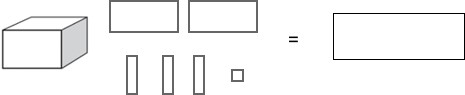
2) If

Write the value of each diagram. (1^st = 1,231)    (2^nd = 2,013)

3) Match the sums that have the same answer.

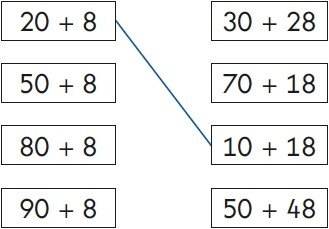
(2nd box to 1st box; 3rd box to 2nd box; 4th box to 4th box)

4) 700 + 20 + 3 =             (723)
3,000 + 40 + 2 =         (3,042)
2,000 + 300 =             (2,300)

Online 1-to-1 maths lessons trusted by schools and teachers
Every week Third Space Learning’s maths specialist tutors support thousands of primary school children with weekly online 1-to-1 lessons and maths interventions. Since 2013 we’ve helped over 150,000 children become more confident, able mathematicians. Learn more or request a personalised quote to speak to us about your needs and how we can help.