Partitioning Explained For Teachers, Parents And Kids

Partitioning is a phrase that even the youngest elementary school child will probably know. Here we show you how kindergarten and 1st grade children are taught this skill to help them break down any number into its component parts.

What is partitioning?

Partitioning is a way of splitting numbers into smaller parts to make them easier to work with. This can also be called decomposing.

Partitioning links closely to place value: a child will be taught to recognize that the number 54 represents 5 tens and 4 ones, which shows how the number can be partitioned into 50 and 4.

By moving tens and ones between the two parts, the number can be partitioned in many other ways:

When shown a number (up to 7+ digits by 5th grade), children should be able to partition them independently to show a good understanding of place value. For example, 5,202,086 = 5,000,000 + 200,000 + 2,000 + 80 + 6.

When will my child learn about partitioning in elementary school?

Children will most likely learn about partitioning very early on in their math lessons.

Schools that follow the Common Core Math State Standards will introduce students to partitioning in Kindergarten. Students will compose and decompose numbers from 11 to 19 into ten ones and some further ones, e.g., by using objects or drawings.

Students will also be expected to write an equation to record their composition or decomposition, such as 10 + 8 = 18. Students expand on this concept in 1st grade, using larger numbers and beginning to apply the same concept to digits within a number.

Students should partition numbers in different ways (for example, 23 = 20 + 3 and 23 = 10 + 13) to support subtraction. They become fluent and apply their knowledge of numbers to reason with, discuss and solve problems that emphasize the value of each digit in two-digit numbers. They begin to understand zero as a placeholder.

In second grade, children use larger numbers to at least 1000, applying partitioning related to place value using varied and increasingly complex problems, building on work in 1st grade (for example, 146 = 100 + 40 and 6, 146 = 130 + 16).

Students in schools who are not following Common Core Standards will also begin to learn how to partition, or compose and decompose, numbers in Kindergarten and build upon that through 1st and 2nd grade. The standards may vary slightly, though.

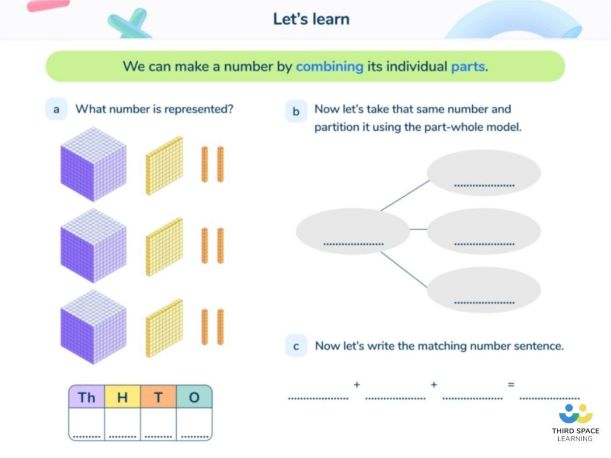
How does partitioning relate to other areas of math?

Children will use partitioning in many other areas of math:

• Introducing column addition, also known as the standard algorithm: 56 + 78 may be first calculated as (50 + 70) + (6 + 8)
• Introducing column subtraction, also known as the standard algorithm: 56 – 22 may be first calculated as (50 – 20) + (6 – 2)
• Understanding exchanging in column subtraction: 32 – 18 may be first calculated as (30 – 10) + (2 – 8) until children realize that they can’t subtract 8 from 2 without reaching a negative number. Partitioning is important here in understanding why exchanging works. 32 can be partitioned into 20 + 12, so this subtraction can be recalculated as (20 – 10) + (12 – 8)
• Introducing multiplication: 34 x 6 may be first calculated as (30 x 6) + (4 x 6) which represents the Distributive Property of Multiplication
• Area Model: Students decompose numbers to make them easier to multiply.

Wondering how to explain other key math vocabulary to your children? Check out our Math Dictionary For Kids And Parents, or try these other terms:

• What Are Equivalent Fractions?
• What Is BODMAS (and BIDMAS)?
• Properties of shapes
• What are 2D shapes?
• What are 3D shapes?
• What Is Part Whole Model?
• What Is Mean In Math?

Practice questions

1) Write the missing numbers.

361 = ___ + 60 + 1 300

945 = 900 + __ + 5     40

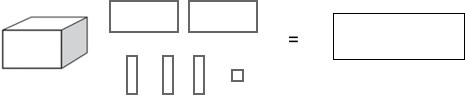
2) If

Write the value of each diagram. (1st = 1,231)    (2nd = 2,013)

3) Match the sums that have the same answer.

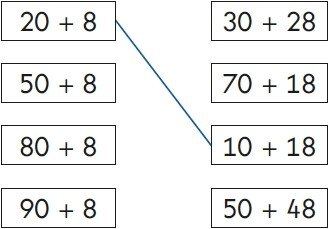
(2nd box to 1st box; 3rd box to 2nd box; 4th box to 4th box)

4) 700 + 20 + 3 =             (723)

3,000 + 40 + 2 =         (3,042)

2,000 + 300 =             (2,300)

Do you have students who need extra support in math?
Give your students more opportunities to consolidate learning and practice skills through personalized math tutoring with their own dedicated online math tutor.

Each student receives differentiated instruction designed to close their individual learning gaps, and scaffolded learning ensures every student learns at the right pace. Lessons are aligned with your state’s standards and assessments, plus you’ll receive regular reports every step of the way.

Personalized one-on-one math tutoring programs are available for:
– 2nd grade tutoring
– 3rd grade tutoring
– 4th grade tutoring
– 5th grade tutoring
– 6th grade tutoring
– 7th grade tutoring
– 8th grade tutoring

Why not learn more about how it works?

The content in this article was originally written by primary school teacher Sophie Bartlett and has since been revised and adapted for US schools by elementary math teacher Katie Keeton.