Equivalent Expressions - Steps, Examples & Questions

[FREE] Fun Math Games & Activities Packs

Always on the lookout for fun math games and activities in the classroom? Try our ready-to-go printable packs for students to complete independently or with a partner!

DOWNLOAD FREE

In order to access this I need to be confident with:

Add and subtract within 100

Integers Order of operations

Math resources Algebra Algebraic expressions

Equivalent expressions

Here you will learn about equivalent expressions, including what they are and how to recognize them.

Students will first learn about equivalent expressions as part of expressions and equations in 6th grade.

What are equivalent expressions?

Equivalent expressions are algebraic expressions that are equal in value.

An algebraic expression is two or more numbers and letters that are combined with mathematical operations such as $+, -,$ or $\div .$

To do this, use properties of operations to create and identify equivalent algebraic expressions.

When stating that two expressions are equivalent we use the equivalence symbol $\equiv$ to show that they are identical.

Addition

Addition is commutative which means changing the order of the terms does not change the sum.

For example, $3x+7y \equiv 7y+3x.$

$3x+7y$ is the same as $7y+3x$ because the coefficients of $x$ are the same, both positive $3x$ and the coefficients of $y$ are the same, both positive $7x.$

This means they are equivalent expressions.

For example, $3a-8b = 3a+(-8b) \equiv -8b+3a.$

The negative sign belongs to the term after it. Subtracting a term is the same as adding a negative term.

$3a-8b$ is the same as $3a+(-8b),$ because subtracting $8b$ is the same as adding $-8b.$ And by the commutative property, $3a+(-8b)$ is the same as $-8b+3a.$

This means they are equivalent expressions.

Multiplication

Multiplication has a distributive property which allows us to break up a number into simpler parts and multiply each part separately. This can be used with variables as well.

For example, $3(x+7) \equiv 3x+21.$

$3(x+7)$ is the same as $3x+21$ because $3 \times x=3x$ , and when you multiply the constants $3$ and $7$ , you get $21.$ The right side is the same as the left side.

This means they are equivalent expressions.

What are equivalent expressions?

Common Core State Standards

How does this relate to 6th and 7th grade math?

Grade 6 – Expressions and Equations (6.EE.A.4)
Identify when two expressions are equivalent (for example, when the two expressions name the same number regardless of which value is substituted into them).
For example, the expressions $y + y + y$ and $3y$ are equivalent because they name the same number regardless of which number $y$ stands for.

Grade 7 – Expressions and Equations (7.EE.A.1)
Apply properties of operations as strategies to add, subtract, factor, and expand linear expressions with rational coefficients.

[FREE] Equivalent Expressions Worksheet (Grade 6 to 8)

Use this worksheet to check your grade 6 to 8 students’ understanding of equivalent expressions. 15 questions with answers to identify areas of strength and support!

DOWNLOAD FREE

[FREE] Equivalent Expressions Worksheet (Grade 6 to 8)

Use this worksheet to check your grade 6 to 8 students’ understanding of equivalent expressions. 15 questions with answers to identify areas of strength and support!

DOWNLOAD FREE

How to identify equivalent expressions

In order to identify equivalent expressions:

Use the properties of operations to create equivalent expressions.
Compare the two expressions.
Make your decision.

Equivalent expressions examples

Example 1: addition and subtraction

Are the expressions $4a+7b$ and $7b-4a$ equivalent?

Use the properties of operations to create equivalent expressions.

Take the first expression and change the order of terms being added: $4a+7b$ becomes $7b+4a.$

Now compare $7b+4a$ and $7b-4a.$

2Compare the two expressions.

The two expressions both have $‘4a’$ and $‘7b’,$ but in the second expression the $‘4a’$ is negative. It is $‘-4a’.$

3Make your decision.

The two expressions are not the same. They are NOT equivalent expressions.

Example 2: distributive property

Are the expressions $4(x-5)$ and $4x-20$ equivalent?

Use the properties of operations to create equivalent expressions.

Take the first expression and multiply the terms within the parentheses by the term on the outside:

$\begin{aligned} & 4(x-5) \\\\ & =4 \times x-4 \times 5 \\\\ & =4 x-20 \end{aligned}$

Compare the two expressions.

The two expressions are the same, $4(x-5) \equiv 4x-20.$

Make your decision.

The two expressions are the same. They are equivalent expressions.

Example 3: combining like terms

Are the expressions $2g + 3t+8g +6$ and $10g + 9t$ equivalent?

Use the properties of operations to create equivalent expressions.

Take the first expression and combine the like terms:

$\begin{aligned} & 2 g+3 t+8 g+6 \\\\ & =2 g+8 g+3 t+6 \\\\ & =10 g+3 t+6 \end{aligned}$

The terms $‘10g’$ and $‘+3t’$ and $‘+6’$ are not like terms. This expression cannot be simplified further.

Now compare $10g + 3t + 6$ and $10g + 9t.$

Compare the two expressions.

The two expressions both have $‘10g’,$ but $‘3t + 6’$ is not the same as $9t.$

Make your decision.

The two expressions are not the same. They are NOT equivalent expressions.

Example 4: two step with distributive property

Are the expressions $3(4+s) + 2$ and $3s + 14$ equivalent?

Use the properties of operations to create equivalent expressions.

Take the first expression and multiply the terms within the parentheses by the term on the outside:

$3(4+s)+2=12+3 s+2$

Then combine the like terms:

$\begin{aligned} & 12+3 s+2 \\\\ & =12+2+3 s \\\\ & =14+3 s \end{aligned}$

Compare the two expressions.

Now compare $14 + 3s$ and $3s + 14.$ The two expressions have $‘14’$ and $‘3s’$ and are addition.

Make your decision.

The two expressions are the same. They are equivalent expressions.

Example 5: equivalent expressions with fractions

Are the expressions $\frac{1}{2} p+5 p-\frac{3}{4}$ and $4 \frac{3}{4} p$ equivalent?

Use the properties of operations to create equivalent expressions.

Take the first expression and combine the like terms:

\begin{aligned} & \frac{1}{2} p+5 p-\frac{3}{4} \\ & =5 \frac{1}{2} p-\frac{3}{4} \end{aligned}

The terms $'5 \frac{1}{2} p' and '-\frac{3}{4}'$ are not like terms. This expression cannot be simplified further.

Compare the two expressions.

Now compare $5 \frac{1}{2} p-\frac{3}{4}$ and $4 \frac{3}{4} p$ .

Both expressions have the variable $p$ , but not the same amount. The first expression also has $-\frac{3}{4}$ .

Make your decision.

The two expressions are not the same. They are NOT equivalent expressions.

Example 6: equivalent expressions with exponents

Are the expressions $y(y-4)$ and $-4 y+y^2$ equivalent?

Use the properties of operations to create equivalent expressions.

Take the first expression and multiply the terms within the parentheses by the term on the outside:

\begin{aligned} & y(y-4) \\ & =y \times y-4 \times y \\ & =y^2-4y \end{aligned}

Compare the two expressions.

Now compare $y^2-4 y$ and $-4 y+y^2$ . The two expressions have a positive $‘y^2’$ and $‘-4 y’$ .

Make your decision.

The two expressions are the same. They are equivalent expressions.

Teaching tips for equivalent expressions

Introduce equivalent expressions through growing shape patterns. Since a growing shape pattern starts with a shape and changes in a constant way from term to term, algebraic expressions can be used to write the pattern’s general rule. Intentionally choosing a pattern that can be solved in more than one way, allows for students to visually see equality among different expressions.

For example,

Write a rule that will find the total number of squares for any term.

The following rules can be written:

$2(n-1) + 5$

$3 + 2n$

$1 + 2(n+1)$

See also: Shape patterns

Review the distributive, associative, and commutative properties with whole numbers, before introducing how to use them with algebraic expressions. Students need a clear understanding of these properties and why they work before they can apply them to variables and integers.

Writing equivalent expressions is a great place to begin with students. Give them an expression and ask them to come up with as many equivalent expressions as possible. Then have them share and justify the equivalence of their expressions with others.

Encourage students to model expressions that have variables by providing digital resources or physical manipulatives (such as algebra tiles). The amount of time that each student needs to spend with these representations will vary, but it is important that students have a conceptual understanding before they begin to solve by manipulating just the numbers and symbols in an expression.

Easy mistakes to make

The order of subtraction is important
Remember that the order of a subtraction equation matters because subtraction is not commutative, so changing the order changes the outcome.

For example,
$7-4$ ≠ $4-7$
$+3$ ≠ $-3$

Mixing up the order of operations (pemdas) for simplifying algebraic expressions
The order of operations should always be used to simplify expressions. For any simple given expression, this means using the distributive property to simplify any parentheses and then combining the like terms from left to right. Doing this in a different order will give the incorrect answer.

For example,

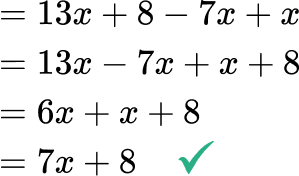
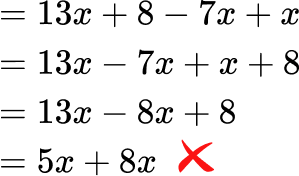
Confusing terms with a coefficient of $\bf{1}$ (or no coefficient)
For terms with a coefficient of $1,$ you don’t need to write the $1,$ but remember that it is still there.

For example,
$1 y=y \hspace{1cm} 1 c+4 m=c+4 m \hspace{1cm} 6(5+1 e)=6(5+e)$

Practice equivalent expressions questions

3a+4b

-3a+4b

4b-3a

-4b+3a

The commutative property says that the order in which the two terms are added can be reversed and the expressions are still equivalent.

$3a-4b=3a+(-4b) \equiv -4b+3a$

3a-12

3a-4

3a+4

3a+12

The commutative property says that the order in which the two terms are added can be reversed and the expressions are still equivalent.

$\begin{aligned} & 3(a+4) \\ & =3 \times a+3 \times 4 \\ & =3 a+12 \end{aligned}$

11xy

6y+5x

5y + 6x

30xy

The commutative property says that the order in which the two terms are added can be reversed and the expressions are still equivalent.

$5x+6y \equiv 6y+5x$

28kh

20kh

13k+15h

5k+15h

Combine the like terms:

$\begin{aligned} & -4 k+11 h+9 k+4 h \\\\ & =-4 k+9 k+11 h+4 h \\\\ & =5 k+15 h \end{aligned}$

8z-32

12z-32

5z + 32

-20z

To create an equivalent expression, multiply the terms within the parentheses by the term on the outside:

$\begin{aligned} & 8(z-4)+4 z \\\\ & =8 \times z-8 \times 4+4 z \\\\ & =8 z-32+4 z \end{aligned}$

Combine the like terms:

$\begin{aligned} & 8 z-32+4 z \\\\ & =8 z+4 z-32 \\\\ & =12 z-32 \end{aligned}$

Equivalent expressions FAQs

Do students need to be able to identify other types of equivalent expressions?

As students continue to learn about equivalent expressions in middle school, they will be introduced to algebraic expressions that have fractions, decimals, and exponents, including quadratic equations. However, it is important that students do not work on more complicated polynomials until they thoroughly understand how to work with simpler expressions.

Can equivalent inequalities also be created?

Yes, the same strategies for creating equivalent expressions and comparing them can be applied to inequalities.

What is the difference between equivalent expressions and equivalent equations?

Both involve two more equivalent entities, but expressions are mathematical statements that do no include the equal sign. An equation on the other hand, includes an equal sign.

The next lessons are

Still stuck?

At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.

Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.