[FREE] Fun Math Games & Activities Packs
Always on the lookout for fun math games and activities in the classroom? Try our ready-to-go printable packs for students to complete independently or with a partner!
Factor tree
Here you’ll learn how to construct factor trees and write a number as a product of prime numbers, including in exponential form.
Students will first learn about factor trees as part of the number system in middle school.
What are factor trees?
Factor trees are a way of expressing the factors of a number, specifically the prime factorization of a number.
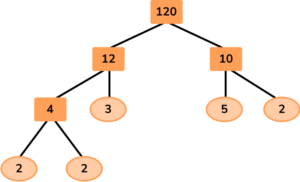
Each branch in the tree is split into factors. Once the factor at the end of the branch is a prime number (only one pair of factors, the number itself and 1), the branch stops and you circle the number.
Factor trees include whole numbers. However, since 1 is not a prime number it will not appear in any factor tree.
To complete factor trees, it is helpful to remember the prime numbers from 1-20:
2, 3, 5, 7, 11, 13, 17, 19, …
Prime factor tree method
To do this, list the factors of a number until the number has been reduced to just prime factors.
For example, here is the factor tree for the number 24:
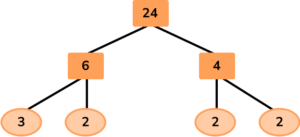
You split the original number 24 into two branches with each factor (6 and 4) being written at the end of the branch. Both 6 and 4 are composite, so two more branches were drawn from each showing their factors.
Since the numbers 3 and 2 are prime numbers, the factor tree is complete.
To write 24 as a product of prime numbers, create an equation using the prime factors from the factor tree:
24=2 \times 2 \times 2 \times 3
It is common practice to write the prime factors in order from smallest to largest.
The product can also be written using exponents for repeated prime factors:
24=2^3 \times 3
What are factor trees?
Common Core State Standards
How does this relate to 6th grade math?
- Grade 6 – The Number System (6.NS.B.4)
Find the greatest common factor of two whole numbers less than or equal to 100 and the least common multiple of two whole numbers less than or equal to 12.
- Grade 6 – Expressions and Equations (6.EE.A.1)
Write and evaluate numerical expressions involving whole-number exponents.
- Grade 6 – Expressions and Equations (6.EE.A.2)
Write, read, and evaluate expressions in which letters stand for numbers.
![[FREE] Factor Tree Worksheet (Grades 6 to 8)](https://thirdspacelearning.com/wp-content/uploads/2023/02/Factor-tree-worksheet-resource-lander-image.webp)
[FREE] Factor Tree Worksheet (Grades 6 to 8)
![[FREE] Factor Tree Worksheet (Grades 6 to 8)](https://thirdspacelearning.com/wp-content/uploads/2023/02/Factor-tree-worksheet-resource-lander-image.webp)
Use this worksheet to check your grade 6 to grade 8 students’ understanding of factor trees. 15 questions with answers to identify areas of strength and support!
DOWNLOAD FREE![[FREE] Factor Tree Worksheet (Grades 6 to 8)](https://thirdspacelearning.com/wp-content/uploads/2023/02/Factor-tree-worksheet-resource-lander-image.webp)
[FREE] Factor Tree Worksheet (Grades 6 to 8)
![[FREE] Factor Tree Worksheet (Grades 6 to 8)](https://thirdspacelearning.com/wp-content/uploads/2023/02/Factor-tree-worksheet-resource-lander-image.webp)
Use this worksheet to check your grade 6 to grade 8 students’ understanding of factor trees. 15 questions with answers to identify areas of strength and support!
DOWNLOAD FREEHow to use a factor tree for prime factorization
In order to use a factor tree for prime factorization:
- Write the number at the top of the factor tree and draw two branches below.
- Fill in the branches with a factor pair of the number above.
- Continue until each branch ends in a prime number.
- Write the solution as a multiplication equation (and if necessary in exponential form).
Factor tree examples
Example 1: standard problem
Express the number 120 as a product of prime factors.
- Write the number at the top of the factor tree and draw two branches below.
Here you write 120 at the top of the tree with two branches below:
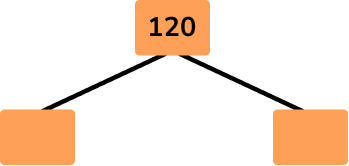
2Fill in the branches with a factor pair of the number above.
The number 120 has many factor pairs. Since the number ends in a 0, it is easy to choose 12 × 10, so you have:
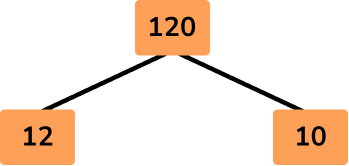
3Fill in the branches with a factor pair of the number above.
Both the numbers 12 and 10 are composite, so two branches are extended from each number and filled in with their factors:
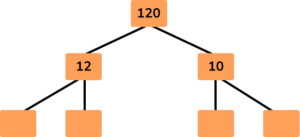
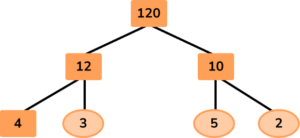
Here the numbers 3, 5 and 2 are prime numbers and so the branches are complete. However, 4 is composite so you need to continue the branches for 4:
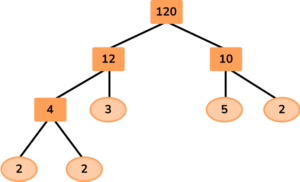
Now each branch ends in a prime number and this factor tree is complete.
4Write the solution as a multiplication equation (and if necessary in exponential form).
Use the numbers from the factor tree to show 120 as a product of prime factors:
120=2 \times 2 \times 2 \times 3 \times 5
Written in exponential form:
120=2^3 \times 3 \times 5
Example 2: standard problem
Express the number 88 as a product of prime factors.
Write the number at the top of the factor tree and draw two branches below.
Here you write 88 at the top of the tree with two branches below:

Fill in the branches with a factor pair of the number above.
The number 88 has many factor pairs. Since it is a multiple of 11, it is easy to choose 8 × 11, so you have:

Continue until each branch ends in a prime number.
11 is prime and 8 is composite, so two branches are extended from 8 and filled in with its factors:
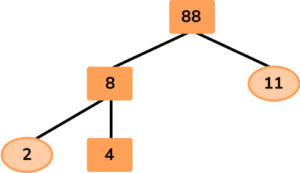
Here, the number 2 is a prime number, so the branch is complete. However, 4 is composite, so you need to continue the branches for 4:
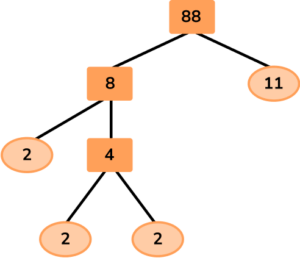
Now each branch ends in a prime number and this factor tree is complete.
Write the solution as a multiplication equation (and if necessary in exponential form).
Use the numbers from the factor tree to show 88 as a product of prime factors:
88=2 \times 2 \times 2 \times 11
Written in exponential form:
88=2^3 \times 11
Example 3: exponential form
The number 242 can be written in the form 242=a\times{b}^2. What are the values of a and b?
Write the number at the top of the factor tree and draw two branches below.

Fill in the branches with a factor pair of the number above.

Continue until each branch ends in a prime number.
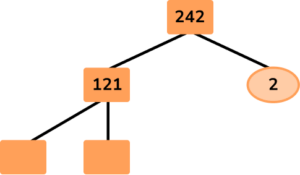
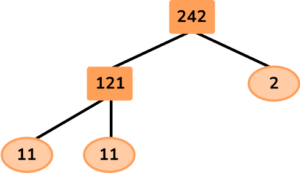
Write the solution as a multiplication equation (and if necessary in exponential form).
242=2 \times 11 \times 11
Written in exponential form:
242=2 \times 11^2
a=2, \ b=11
Example 4: unique factor tree
Complete the diagram to find the missing product and show it as a product of prime factors.
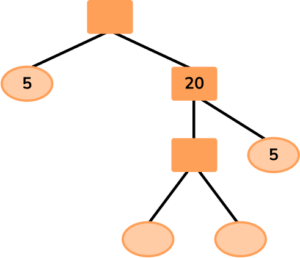
Write the number at the top of the factor tree and draw two branches below.
The number at the top of the tree is the product of the branches below. This means that the number you are expressing is equal to: 5 × 20 = 100.
Fill in the branches with a factor pair of the number above.
Looking further down the tree, you can see that the number 20 is split into two factors. One of those factors is equal to 5 therefore the other factor must be:
20 ÷ 5 = 4
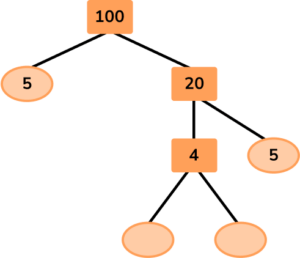
Continue until each branch ends in a prime number.
The only factor pair of 4 that does not include 1 is 2 × 2 = 4 therefore the two values in the branches are equal to 2:
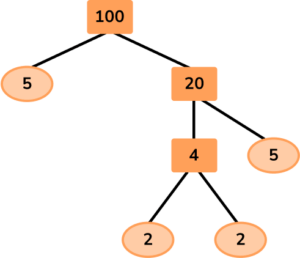
Write the solution as a multiplication equation (and if necessary in exponential form).
100=2 \times 2 \times 5 \times 5
Written in exponential form:
100=2^2 \times 5^2
Example 5: multiple steps
Given that 72 = 9 × 8, write 72 as a product of prime factors in exponential form.
Write the number at the top of the factor tree and draw two branches below.

Fill in the branches with a factor pair of the number above.
Here, the question has told us to use the factor pair 9 × 8.

Continue until each branch ends in a prime number.
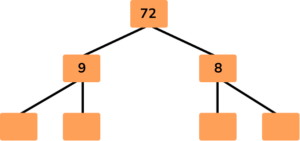
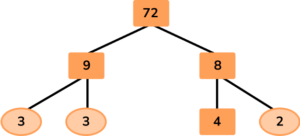
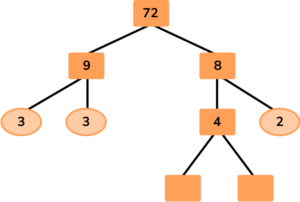
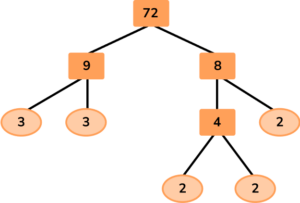
Write the solution as a multiplication equation (and if necessary in exponential form).
72=2 \times 2 \times 2 \times 3 \times 3
Written in exponential form:
72=2^3 \times 3^2
Example 6: powers of 2
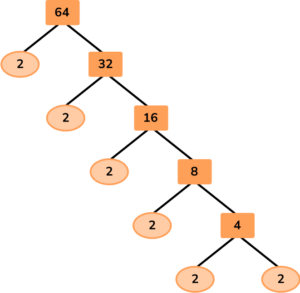
Express the number 64 as a power of 2.
Write the number at the top of the factor tree and draw two branches below.
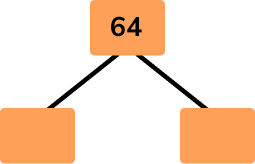
Fill in the branches with a factor pair of the number above.
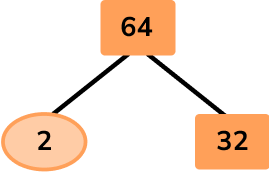
Continue until each branch ends in a prime number.
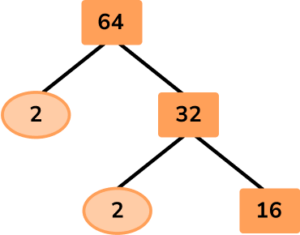
Keep going…
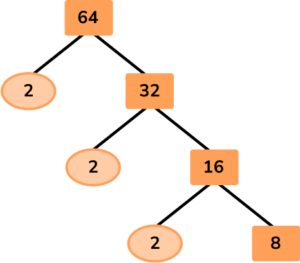
Nearly there…
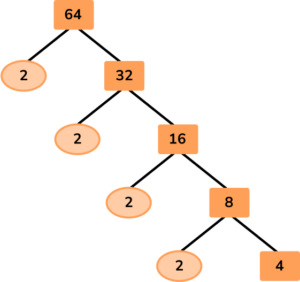
One more step…
Great! You got there!
Write the solution as a multiplication equation (and if necessary in exponential form).
64=2 \times 2 \times 2 \times 2 \times 2 \times 2
Written in exponential form:
64=2^6
This is an example of relying on the number being even which generates a very long, and time consuming factor tree. This is not incorrect, it just takes a lot of time to get to the solution with the potential to make a simple mistake.
Here are two alternatives to the same factor tree:
Version 1
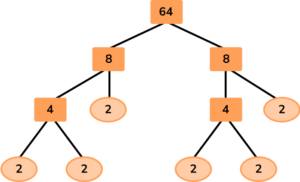
Version 2
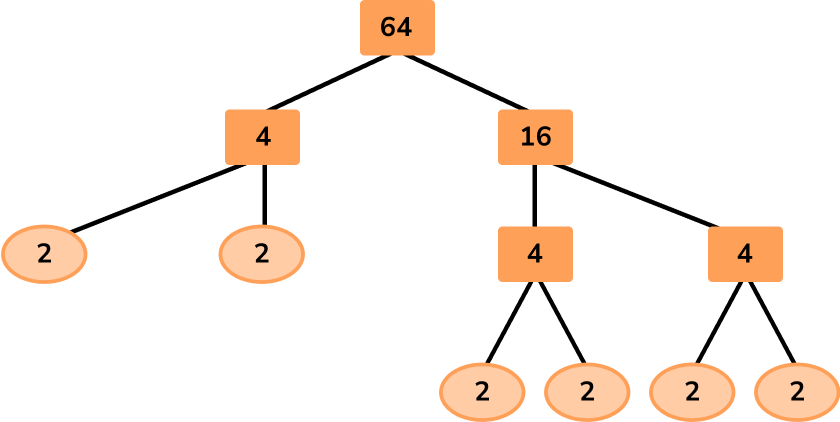
Teaching tips for factor trees
- Before teaching factor trees, spend time on prime number activities to help students more easily recognize them. It also may be helpful to review divisibility rules, to help students identify factors quicker.
- Encourage students to create different factor trees for the same number (as shown in Example 6). Students can then compare and contrast the trees and identify patterns.
- Instead of just using factor tree worksheets, let students solve using white boards or by incorporating them into a game.
- Give students practice building a factor tree backwards based on a set of given numbers; solving for the product (as shown in Example 5).
Easy mistakes to make
- Using addition instead of multiplication
For example, students will incorrectly write the factors of 26 as 13 and 13 (thinking about 13+13=26 ). However since factors are multiplied together, 13×13=169, it is clear the product is not 26.
- Thinking a number is prime when it is not, or composite when it is not
There are several composite numbers that are often mistaken as prime numbers. Here are a couple of them: 1, 9, 15, 21, 27. This confusion typically occurs with multiples of 3 and 7.
- Not writing the final equation
It is a simple mistake to make but after completing the factor tree, you must write the number as a product of its factors, otherwise you have demonstrated a method but not answered the question (such as using grid multiplication and not adding up the values in the grid for your final solution).
- Getting confused when drawing a large factor tree
Space out the diagram so you can clearly see all the factors, and circle / underline / use a highlighter to highlight the prime factors for your solution, carefully check how many of each prime number exist, then simplify. The order does not matter but the final solution does!
Related lessons on factors and multiples
Practice factor trees questions
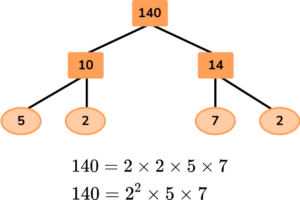
1. Write 140 as a product of its prime factors.




Here is one example of a factor tree for 140. Note that there are other factor trees, but they all end with the same prime factors.
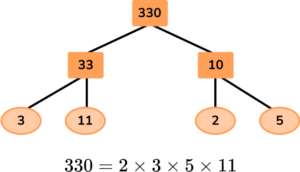
2. Write 330 as a product of its prime factors.




Here is one example of a factor tree for 330. Note that there are other factor trees, but they all end with the same prime factors.
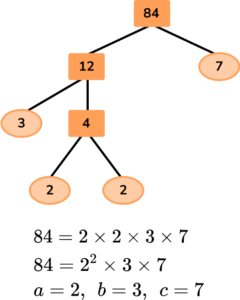
3. Find the values of a, b, and c where
84 = a^{2} \times b \times c




Here is one example of a factor tree for 84. Note that there are other factor trees, but they all end with the same prime factors.
4. Spot the mistake in the following calculation
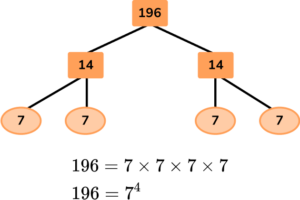
196 should be split into 2 and 98

14 should be split into 2 and 7

7 should be split into 1 and 7

There is no mistake – the solution is correct

A factor tree shows multiplication factors. Since 14=2\times{7}, \ 14 should be split into 2 and 7. The tree should look like this:
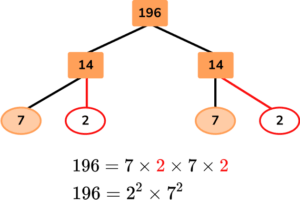
The tree could also be split into 2 and 98, but the question asked for a mistake – not a different way to solve.
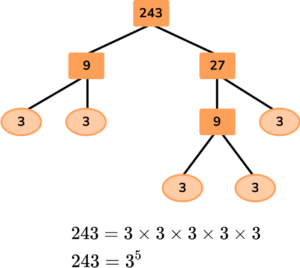
5. Write the number 243 as a power of 3.




Here is one example of a factor tree for 243. Note that there are other factor trees, but they all end with the same prime factors.
6. Assume a and b are prime numbers. Expand fully 35a^{2}b to show it as a product of prime numbers.




Here is the factor tree for 35a^{2}b.
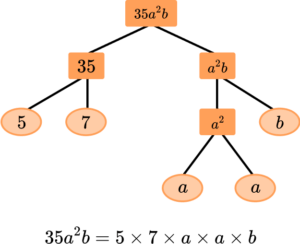
Remember: when you write algebraic expressions, you write numbers and then letters in alphabetical order.
Factor tree FAQs
No, a factor is a number that divides into another number with no left overs, so they involve only whole numbers.
It can be used to find the greatest common factor (GCF), the least common multiple (LCM) and other numerical properties such as whether the number is square, cube or prime.
A factor tree is complete when all the numbers at the bottom level are prime numbers. A factor tree is a visual representation of the prime factorization of a number, where you continue to break down the number into its prime factors until you reach only prime numbers.
While some calculators may have built-in functions for finding factor trees, not all calculators provide this feature. Basic calculators focus on arithmetic operations and do not include functions for factorization. However, if you have access to a graphing calculator or a scientific calculator, there might be applications available that can help you find factor trees or prime factorizations.
The next lessons are
Still stuck?
At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.
Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.

Find out how we can help your students achieve success with our math tutoring programs.
[FREE] Common Core Practice Tests (Grades 3 to 6)
Prepare for math tests in your state with these Grade 3 to Grade 6 practice assessments for Common Core and state equivalents.
40 multiple choice questions and detailed answers to support test prep, created by US math experts covering a range of topics!