[FREE] Fun Math Games & Activities Packs
Always on the lookout for fun math games and activities in the classroom? Try our ready-to-go printable packs for students to complete independently or with a partner!
In order to access this I need to be confident with:
Place valueDecimal system
Addition and subtraction Powers of ten Multiplication and division Fractions Equivalent fractionsMixed numbers
Decimals
Here you will learn about decimal numbers including how to read and write them, understand their place value, and strategies to compare them.
Students will first learn about decimals in 4th grade math as part of their work in number and operations with fractions and extend their knowledge as they work through number systems in middle school.
What are decimals?
Decimals are numbers that have a whole part and a fractional part that are separated by a decimal point. Our decimal system splits whole numbers into tenths, hundredths, thousandths, and so on.
This decimal place value chart can help you understand decimal place value.
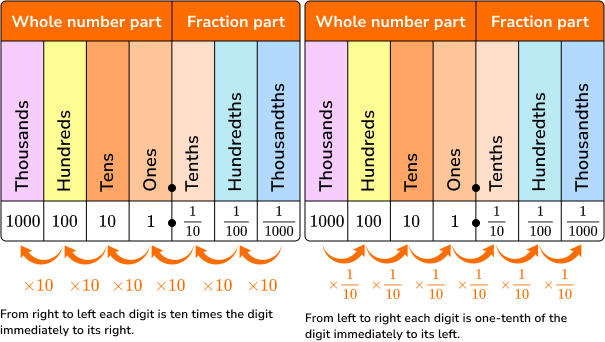
Step-by-step guide: Decimal place value
Step-by-step guide: Decimal places
You can convert fractions to decimals and decimals to fractions.
Fractions as decimals \hspace{1.7cm}
Fraction → \cfrac{3}{10}
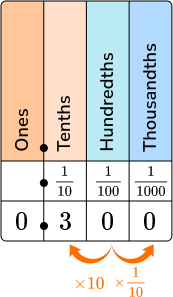 | Fraction → \cfrac{3}{100}
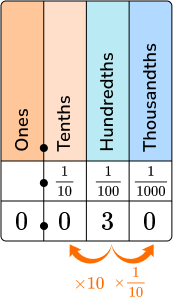 | Fraction → \cfrac{3}{1000}
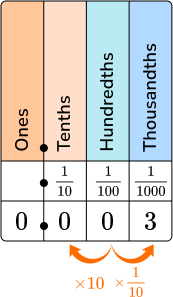 |
Decimals as fractions \hspace{1.7cm}
Decimal → 0.43
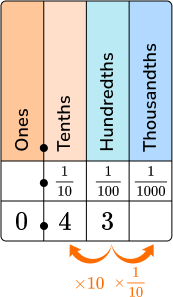 Read as forty-three hundredths.
| Decimal → 0.009
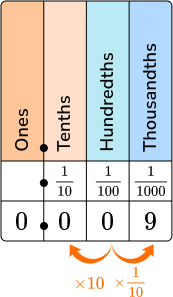 Read as nine thousandths.
|
You can compare decimal numbers using a place value chart or converting them to fractions.
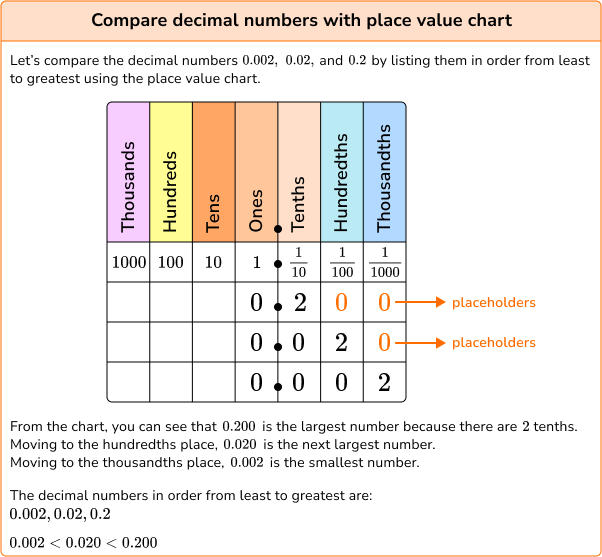
| Comparing decimals with equivalent fractions |
|---|
Let’s compare 0.009, \, 0.09 and 0.9 by listing them in order from least to greatest.
|
Step by step guide: Comparing decimals
![[FREE] Decimals Worksheet (Grades 4 to 6)](https://thirdspacelearning.com/wp-content/uploads/2023/03/elementary-math-quizzes.png)
[FREE] Decimals Worksheet (Grades 4 to 6)
![[FREE] Decimals Worksheet (Grades 4 to 6)](https://thirdspacelearning.com/wp-content/uploads/2023/03/elementary-math-quizzes.png)
Use this quiz to check your grade 4 to 6 students’ understanding of decimals. 10+ questions with answers covering a range of 4th, 5th and 6th grade topics to identify areas of strength and support!
DOWNLOAD FREE![[FREE] Decimals Worksheet (Grades 4 to 6)](https://thirdspacelearning.com/wp-content/uploads/2023/03/elementary-math-quizzes.png)
[FREE] Decimals Worksheet (Grades 4 to 6)
![[FREE] Decimals Worksheet (Grades 4 to 6)](https://thirdspacelearning.com/wp-content/uploads/2023/03/elementary-math-quizzes.png)
Use this quiz to check your grade 4 to 6 students’ understanding of decimals. 10+ questions with answers covering a range of 4th, 5th and 6th grade topics to identify areas of strength and support!
DOWNLOAD FREEYou can place decimals on a number line to help visualize the value of decimals.
| Decimal on a number line |
|---|
A decimal number line is a number line that includes decimal increments and can help 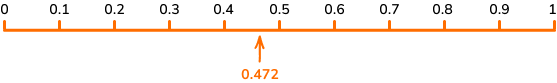 If you zoom in on the number line between 0.4 and 0.5 that goes up in steps of 0.01  |
Step by step guide: Decimal number line
You can perform calculations on decimal numbers like you would with multi-digit numbers.
Adding and subtracting decimals \hspace{1.7cm}
Add: 3.87 + 4.21 =
\, ?
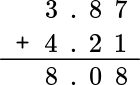 ● Line up the decimal points
| Subtract: 5.6- 3.79 = \, ?
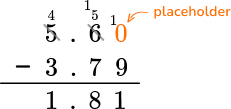 ● Line up the decimal points
|
Step by step guide: Adding decimals
Step by step guide: Subtracting decimals
Step by step guide: Adding and subtracting decimals
Multiplying and dividing decimals \hspace{1.7cm}
Multiply: 0.34\times 3 =
\, ?
● Put the number with the most amount of  | Divide: 1.10\div 2 =
\, ?
● Line up the decimal point of the dividend 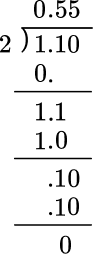 |
Step by step guide: Multiplying decimals
Step by step guide: Dividing decimals
Step by step guide: Multiplying and dividing decimals
What are decimals?

Common Core State Standards
How does this relate to 4th grade math, 5th grade math, and 6th grade math?
- Grade 4 – Number and Operations Fractions (4.NF.C.7)
Compare two decimals to hundredths by reasoning about their size. Recognize that comparisons are valid only when the two decimals refer to the same whole. Record the results of comparisons with the symbols >, =, or < , and justify the conclusions, example, by using a visual model.
- Grade 5 – Number and Operations Base Ten (5.NBT.A.3)
Read, write, and compare decimals to thousandths.
- Grade 5 – Number and Operations in Base Ten (5.NBT.A.1)
Recognize that in a multi-digit number, a digit in one place represents 10 times as much as it represents in the place to its right and \frac{1}{10} of what it represents in the place to its left.
- Grade 5 – Number and Operations in Base Ten (5.NBT.B)
Perform operations with multi-digit whole numbers and with decimals to hundredths.
- Grade 6: The Number System (6.NS.B.3)
Fluently add, subtract, multiply, and divide multi-digit decimals using the standard algorithm for each operation.
How to write decimal numbers
In order to write a fraction as a decimal:
- Write the fraction in words.
- Place the numerator of the fraction on the place value chart.
- Write the decimal number.
In order to write a decimal as a fraction:
- Write the decimal in words.
- The digits of the decimal is the numerator, and the denominator is the column of the last digit on the place value chart.
- Write the fraction and simplify if possible.
Decimals examples
Example 1: write the fraction as a decimal
Change \cfrac{47}{100} \, to a decimal number.
- Write the fraction in words.
\cfrac{47}{100} \, is 47 hundredths.
2Place the numerator of the fraction in the correct spaces on the place value chart.
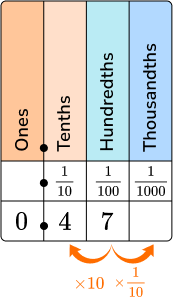
3Write the decimal number.
\cfrac{47}{100} \, as a decimal is 0.47.
Example 2: writing a decimal as a fraction
Write 0.017 as a fraction.
Write the decimal in words.
0.017 is seventeen thousandths.
The digits of the decimal is the numerator, and the denominator is the column of the last digit on the place value chart.
0 is in the tenths column, 1 is in the hundredths column and 7 is in the thousandths column.
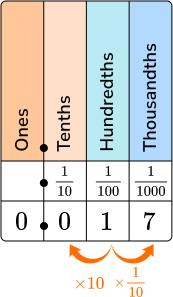
17 is the numerator, and 1000 will be the denominator.
Write the fraction.
Example 3: comparing decimals using a place value chart
Use the place value chart to list these decimal numbers in order from least to greatest.
0.05, 0.02, 0.205, 0.052, 0.502
Put the number on the place value chart.
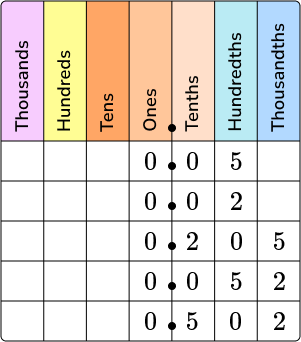
Add zeros as place holders as necessary.
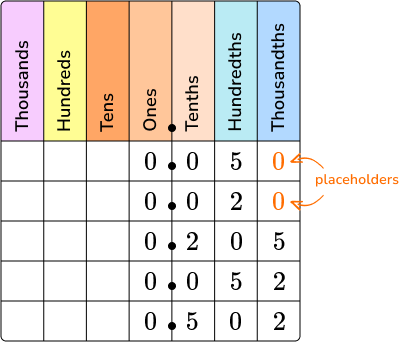
Start with the tenths place to compare numbers.
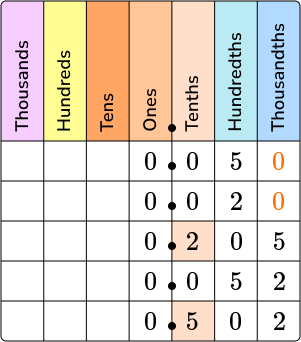
From the chart, you can see that 0.502 is the greatest value decimal number, and then 0.205.
0.050, 0.020, and 0.052 all have 0 ’s in the tenths place which means they are lesser in value than 0.205 and 0.502.
Next, move on to the hundredths place and then the thousandths place.
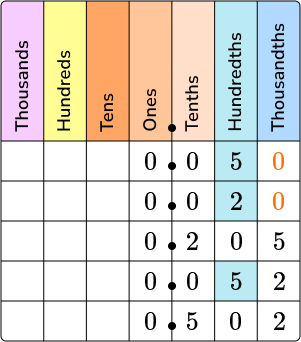
Moving to the hundredths place on the chart, you can see that 0.020 is less than 0.050 and 0.052.
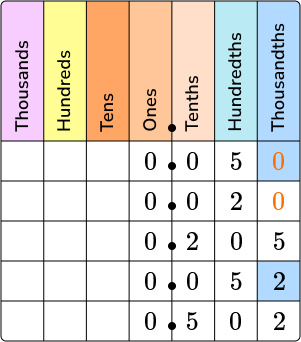
Moving to the thousandths place on the chart, you can see that 0.050 is less than 0.052.
Write the decimal numbers in the correct order.
The decimal numbers in order from least to greatest is:
0.020, \, 0.050, \, 0.052, \, 0.205, \, 0.502
0.020 < 0.050 < 0.052 < 0.205 < 0.502
Example 4: comparing decimals using equivalent fractions
List the decimals in order from least to greatest, using equivalent fractions.
0.4, \, 0.004, \, 0.44, \, 0.04
Rewrite the decimals as fractions
0.4 is 4 tenths → \cfrac{4}{10}
0.004 is 4 thousandths → \cfrac{4}{1000}
0.44 is 44 hundredths → \cfrac{44}{100}
0.04 is 4 hundredths → \cfrac{4}{100}
Use equivalent fractions to get a common denominator.
Use equivalent fractions to get a common denominator of 1000.
\cfrac{4}{10}=\cfrac{4 \, \times \, 100}{10 \, \times \, 100}=\cfrac{400}{1000}
\cfrac{4}{1000} \, has a denominator of 1000.
\cfrac{44}{100}=\cfrac{44 \, \times \, 10}{100 \, \times \, 10}=\cfrac{440}{1000}
\cfrac{4}{100}=\cfrac{4 \, \times \, 10}{100 \, \times \, 10}=\cfrac{40}{1000}
Write the fraction numbers in order or use \textbf{>, <, =} to compare them.
Now that the denominators are all 1000, it will be easier to compare the numbers.
\cfrac{4}{1000}, \, \cfrac{40}{1000}, \, \cfrac{400}{1000}, \, \cfrac{440}{1000}
\cfrac{4}{1000} \, < \, \cfrac{40}{1000} \, < \, \cfrac{400}{1000} \, < \, \cfrac{440}{1000}
Write the decimal numbers in order or use \textbf{>, <, =} to compare them.
\begin{aligned} &\cfrac{4}{1000}, \, \cfrac{40}{1000}, \, \cfrac{400}{1000}, \, \cfrac{440}{1000} \\\\ & \hspace{0.2cm} ↓ \hspace{0.8cm} ↓ \hspace{0.8cm} ↓ \hspace{0.7cm}↓ \\\\ &0.004, \, 0.040, \, 0.400, \, 0.440 \end{aligned}
0.004 \, < \, 0.040 \, < \, 0.400 \, < \, 0.440
Example 5: add decimal numbers
Add the decimal numbers,
5.4 + 1.27
Stack the numbers and line up the decimal points (and place value).
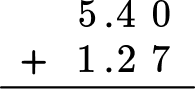
Add each column from right to left and regroup the numbers when necessary.
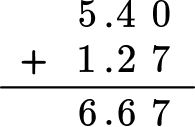
Write your final answer with the decimal point and check to make sure your answer is reasonable.
5.4 rounds to 5 and 1.26 rounds to 1.
5 + 1 = 6 so 6.67 is reasonable.
Example 6: multiply decimal numbers
Multiply the decimal numbers,
3.2\times 4.03
Stack the number with the most digits on top.

Multiply as if the numbers were multi-digit whole numbers, regrouping when necessary.
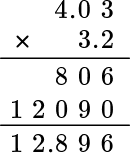
Count the number of digits after the decimal point for each factor.

Put the same number of digits after the decimal point for the product.
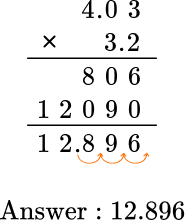
Teaching tips for decimals
- Using visual models such as number lines or place value representation helps students build number sense as they learn decimal place values.
- Although decimal worksheets have their place in the classroom, utilizing online platforms for game playing helps to motivate students and also provides time for them to practice.
- Reinforcing placeholder 0 ’s makes the decimal numbers have the same digits so that students can easily compare them. It also builds understanding for decimal operations.
Easy mistakes to make
- Confusing decimal numbers
For example,
When comparing 0.50 and 0.05 and thinking they are both 5 hundredths or 5 tenths.
- Forgetting to use to placeholder \bf{0} ’s when comparing decimals
- Adding \bf{0} ’s placeholders in the wrong place
For example,
Adding the 0 ’s as placeholders before the 9 in the decimal number 0.9 instead of after the 9.
Practice decimals questions
1. Which decimal represents the fraction \cfrac{17}{100}?




\cfrac{17}{100} \, is 17 hundredths.
Place 1 in the tenths column and 7 in the hundredths column.
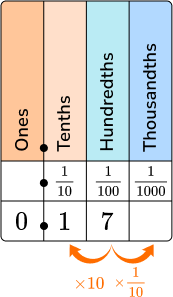
The decimal number is 0.17.
2. Which fraction represents the decimal 0.092?




0.092 is ninety-two thousandths. Place the decimal number on the place value chart, 0 in the tenths column, 9 in the hundredths column and 2 in the thousandths column.
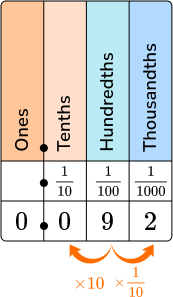
92 is the numerator of the fraction, and 1000 will be the denominator of the fraction.
\cfrac{92}{1000}
3. Write the decimals in order from least to greatest using a place value chart.
0.46, \, 0.06, \, 0.5, \, 0.4




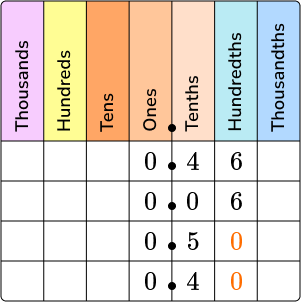
You can see from the chart that 0.06 has the smallest value and 0.50 has the greatest value.
You can also see from the hundredths column that 0.46 is larger than 0.40.
The numbers in order from least to greatest are:
0.06, \, 0.40, \, 0.46, \, 0.50
0.06 < 0.40 < 0.46 < 0.50
4. Write the decimals in order from least to greatest using equivalent fractions.
0.66, \, 0.116, \, 0.16, \, 0.6




Write each decimal as a fraction.
0.66 is 66 hundredths which is \, \cfrac{66}{100}.
0.116 is 116 thousandths which is \, \cfrac{116}{1000}.
0.16 is 16 hundredths which is \, \cfrac{16}{100}.
0.6 is 6 tenths which is \cfrac{6}{10}.
The common denominator is 1000; use equivalent fractions to rewrite fractions with the denominator 1000.
\cfrac{66}{100}=\cfrac{66\times 10}{100\times 10}=\cfrac{660}{1000}
\cfrac{116}{1000} \, has a denominator of 1000.
\cfrac{16}{100}=\cfrac{16\times 10}{100\times 10}=\cfrac{160}{1000}
\cfrac{6}{10}=\cfrac{6\times 100}{10\times 100}=\cfrac{600}{1000}
The fractions are easier to compare when they have the same denominator.
The fractions in order from least to greatest are:
\cfrac{116}{1000}, \, \cfrac{160}{1000}, \, \cfrac{600}{1000}, \, \cfrac{660}{1000}
Ordering decimals in order from least to greatest are:
0.116, \, 0.16, \, 0.6, \, 0.66
5. Add: 6.07 + 0.4.




Line up the decimal points.

Add placeholder 0 ’s where necessary. Then add the numbers the same way you would add multi-digit numbers.

6. Multiply: 7.3\times 0.4.




Place the number with the greatest number of digits on top. Multiply the numbers the way you would multi-digit numbers.
Count the total number of digits to the right of the decimal point in both numbers. Make sure the answer has the same number of total digits to the right of the decimal point.

Move the decimal point two places so that there is 2 digits to the right of the decimal point.
![]()
The answer is 2.92.
Decimals FAQs
Yes, using a number line is another visual strategy to compare decimals. Comparing 0.2 and 0.6 on the number line, you can see that 0.2 is closer to 0 and 0.6 is further to the right. This means that 0.6 is the larger number. The further right a number is on the number line the larger it is.
Decimal place value is important because it provides a foundation for the decimal system and decimal operations.
Decimals and fractions are very similar because they both have a whole part and a fraction part.
A decimal fraction is when the denominator of the fraction is a power of 10.
For example, \cfrac{3}{100} \, is a decimal fraction because 100 is 10^2.
Yes, decimal numbers bigger than 1 are similar to mixed numbers.
For example, 1.3 can be represented as the mixed number 1\cfrac{3}{10}.
The digits to the left of the decimal point represent ones, tens, hundreds, etc. The numbers to the right of the decimal point represent tenths, hundredths, thousandths, etc.
The next lessons are
Still stuck?
At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.
Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.

Find out how we can help your students achieve success with our math tutoring programs.
[FREE] Common Core Practice Tests (Grades 3 to 6)
Prepare for math tests in your state with these Grade 3 to Grade 6 practice assessments for Common Core and state equivalents.
40 multiple choice questions and detailed answers to support test prep, created by US math experts covering a range of topics!