[FREE] Fun Math Games & Activities Packs
Always on the lookout for fun math games and activities in the classroom? Try our ready-to-go printable packs for students to complete independently or with a partner!
In order to access this I need to be confident with:
Adding and subtracting
Skip counting Decimals Place valueMultiplication and division
Here you will learn about multiplication and division, including strategies on how to multiply and divide various types of rational numbers.
Students first learn about multiplication and division in the 3 rd grade and 4th grade with their work with operations and algebraic thinking, as well as number and operations base ten and fractions.
What is multiplication and division?
Multiplication and division are two of the four basic operations. Multiplication is finding the product of two or more numbers, and division is finding the quotient of two numbers.
Multiplication is basically the repeated addition of equal groups.
For example, 4 equal groups of 3 :
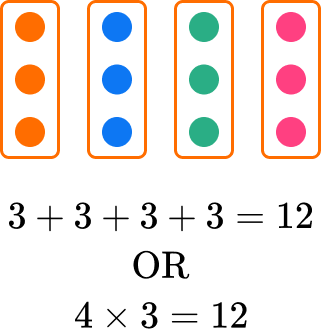
In a multiplication equation, the answer to multiplying one number by another is called the product. The multiplicand is the quantity to be multiplied by the multiplier, which will give you a product.

The product will be 0 if either the multiplicand or multiplier is 0 .
Arrays are visual models that represent multiplication.
For example, this array shows 3 rows of 6 which is the same as 3 \times 6 .

3 \times 6=18
Step by step guide: Understanding Multiplication
Multiplication is commutative. The order in which the calculation is performed does not matter.
For example,
3\times{4}=4\times{3}=12
Multiplying multi-digit numbers
To multiply multi-digit numbers, you can use the algorithm or the area model.
The area model is a rectangular model where the product represents finding the area of the rectangle.
For example, multiply 42 \times 62 using an area model.
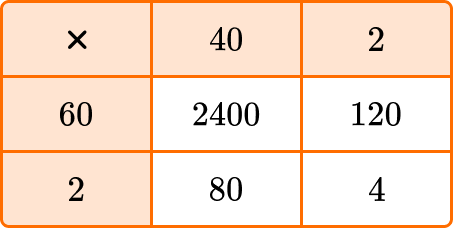
2400+120+80+4=2604
42 \times 62=2604
Step-by-step guide: Multiplying multi-digit numbers
Multiplicative comparisons
You can use multiplication to make comparisons between quantities. Multiplicative comparisons compare two quantities by showing that one quantity is how many times larger or smaller than another quantity.
For example,
Mike has 3 lollipops. Michelle has 4 times as many lollipops as Mike. How many lollipops does Michelle have?
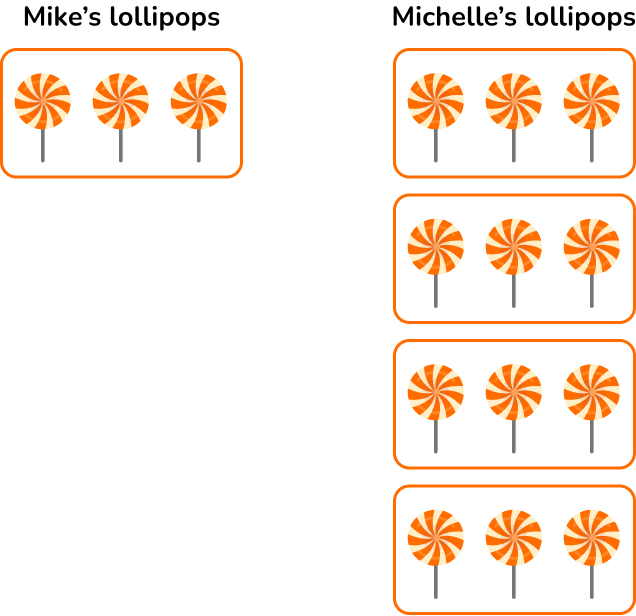
Michelle has 4\times 3=12 lollipops.
Jillian has 24 inches of hair ribbon. Suzanne has half that amount. How long is Suzanne’s hair ribbon?

Suzanne’s ribbon is \cfrac{1}{2} \times 24=12 \text { inches }
Step by step guide: Multiplicative comparisons
![[FREE] Multiplication and Division Worksheet (Grade 4, 5 and 7)](https://thirdspacelearning.com/wp-content/uploads/2023/11/Multiplication-and-Division-Check-for-Understanding-listing-image.png)
[FREE] Multiplication and Division Worksheet (Grade 4, 5 and 7)
![[FREE] Multiplication and Division Worksheet (Grade 4, 5 and 7)](https://thirdspacelearning.com/wp-content/uploads/2023/11/Multiplication-and-Division-Check-for-Understanding-listing-image.png)
Use this quiz to check your grade 4, 5 and 7 students’ understanding of multiplication and division. 10+ questions with answers covering a range of 4, 5 and 7 grade multiplication and division topics to identify areas of strength and support!
DOWNLOAD FREE![[FREE] Multiplication and Division Worksheet (Grade 4, 5 and 7)](https://thirdspacelearning.com/wp-content/uploads/2023/11/Multiplication-and-Division-Check-for-Understanding-listing-image.png)
[FREE] Multiplication and Division Worksheet (Grade 4, 5 and 7)
![[FREE] Multiplication and Division Worksheet (Grade 4, 5 and 7)](https://thirdspacelearning.com/wp-content/uploads/2023/11/Multiplication-and-Division-Check-for-Understanding-listing-image.png)
Use this quiz to check your grade 4, 5 and 7 students’ understanding of multiplication and division. 10+ questions with answers covering a range of 4, 5 and 7 grade multiplication and division topics to identify areas of strength and support!
DOWNLOAD FREEMultiplying rational numbers
You can multiply rational numbers. Rational numbers include multi-digit numbers, integers, fractions, and decimals. When multiplying positive and negative numbers, the following rules apply:
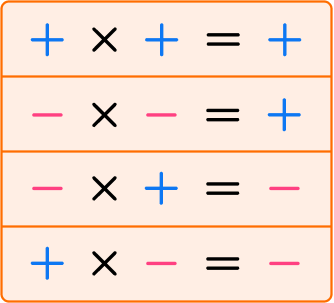
For example, (-3) \times(-5)=15
Step by step guide: Multiplying and dividing integers
Division
Division shares or breaks a number into equal sized groups.
For example, the number 12 can be divided into 4 equal groups of 3 .
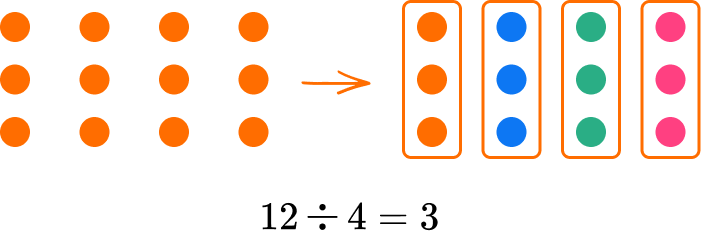
In a division equation, the answer you get when you divide one number by another is called the quotient.
The word quotient comes from Latin and means ‘how many times.’ When dividing, you are finding out ‘how many times’ a number goes into another number.
For example,

The quotient will only be 0 if the dividend is 0 but the divisor is not.
For example,
0 \div 8=0
8 \div 0=\text {Does not exist }
Step by step guide: Understanding division
Unlike multiplication, division is not commutative. If the order of the numbers within the calculation changes, the result will change.
12 \div 4
To solve division problems with larger numbers, you can use long division.
For example, 452.1 \div 3
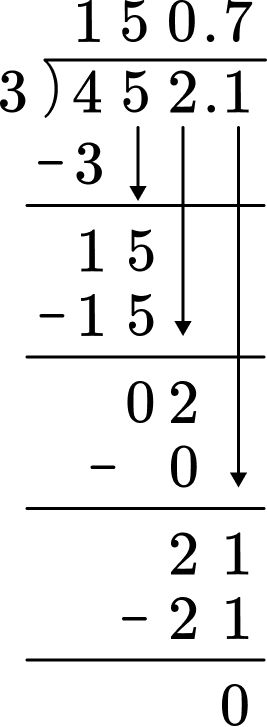
Step-by-step guide: Long division
Step by step guide: Dividing multi-digit numbers
Division can also be done with positive and negative integers, fractions, and decimals. When dividing positive and negative numbers, the following rules apply:
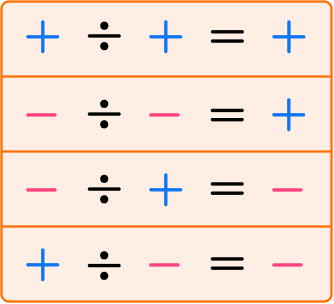
For example, (-20) \div (-5)=4
Step by step guide: Multiplying and dividing integers
Step by step guide: Multiplying and dividing rational numbers
What is multiplication and division?
Common Core State Standards
How does this relate to 4 th – 7 th grade math?
- Grade 3: Operations and Algebraic Thinking ( 3.OA.A.1)
Interpret products of whole numbers, for example, interpret 5 × 7 as the total number of objects in 5 groups of 7 objects each.
- Grade 3: Operations and Algebraic Thinking (3.OA.A.2)
Interpret whole-number quotients of whole numbers, for example, interpret 56 \div 8 as the number of objects in each share when 56 objects are partitioned equally into 8 shares, or as a number of shares when 56 objects are partitioned into equal shares of 8 objects each.
- Grade 3: Operations and Algebraic Thinking (3.OA.C.7)
Fluently multiply and divide within 100 , using strategies such as the relationship between multiplication and division.
- Grade 4: Operations and Algebraic Thinking (4.OA.2)
Multiply or divide to solve word problems involving multiplicative comparison, for example, by using drawings and equations with a symbol for the unknown number to represent the problem, distinguishing multiplicative comparison from additive comparison.
- Grade 4: Number and Operations – Fractions (4.NF.B.4)
Apply and extend previous understandings of multiplication to multiply a fraction by a whole number.
- Grade 5: Number and Operations Base Ten (5.NBT.B.5)
Fluently multiply multi-digit whole numbers using the standard algorithm.
- Grade 5: Number and Operations – Fractions (5.NF.B.7)
Apply and extend previous understandings of division to divide unit fractions by whole numbers and whole numbers by unit fractions.
- Grade 6: Number System (6.NS.C.6)
Understand a rational number as a point on the number line. Extend number line diagrams and coordinate axes familiar from previous grades to represent points on the line and in the plane with negative number coordinates.
- Grade 7: Number System (7.NS.A.2)
Apply and extend previous understandings of multiplication and division and of fractions to multiply and divide rational numbers.
How to do multiplication and division
There are several strategies to multiply and divide numbers. For more specific step-by-step guides, check out the individual pages linked in the “What is multiplication and division?” section above or read through the examples below.
In order to multiply using a visual model:
- Draw the array.
- Count the objects in each row.
- Find the total.
In order to divide using a visual model:
- Draw the array.
- Count the objects in each group.
- Write the answer.
In order to multiply and divide multi-digit numbers:
- Perform the multiplication or division algorithm.
- Write the answer.
In order to find multiplicative comparisons:
- Draw a model.
- Write an equation.
- Solve the equation and label the answer.
Multiplication and division examples
Example 1: multiply using a model
Use a visual model to multiply 5 \times 3.
- Draw the array.
5 x 3 is 5 rows of 3.

2Count the objects in each row.
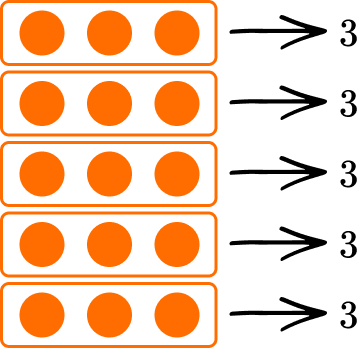
3Find the total.
There are 3 chips in each row, 3+3+3+3+3=15
3 \times 5=15
Example 2: multiply using algorithm
Multiply 99 \times 7.
Perform the multiplication or division algorithm.
Using the algorithm,
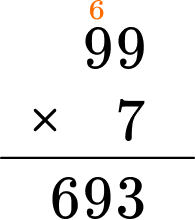
Write the answer.
99 \times 7=693
Example 3: multiply and divide rational numbers
Multiply 1.23 \times 3.2.
Perform the multiplication or division algorithm.
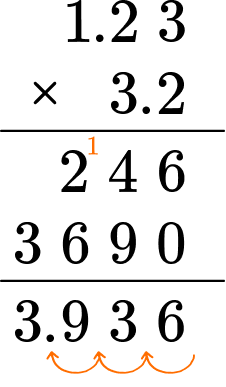
Write the answer.
1.23 \times 3.2=3.936
Example 4: divide using a visual model
Divide: 9 \div 3
Draw the array.

Count the objects in each group.
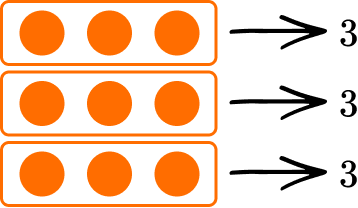
Write the answer.
9 \div 3=3
Example 5: dividing rational numbers
Divide: 15.4 \div 2
Perform the multiplication or division algorithm.
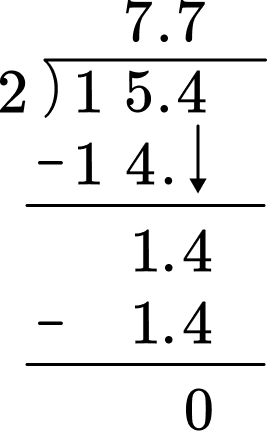
Write the answer.
15.4 \div 2=7.7
Example 6: multiplicative comparison
Bobby has 3 baseball cards. Joey has five times as many cards as Bobby. How many cards does Joey have?
Draw a model.

Write an equation.
3 \times 5= \, ?
Solve the equation and label the answer.
3 \times 5=15
Joey has 15 baseball cards.
Teaching tips for multiplication and division
- Use manipulatives to reinforce the conceptual understanding of multiplication and division.
- Include real world scenarios so that students can connect the mathematical concepts to the world around them.
- Reinforce to students that the concept of multiplication and division is the same regardless if the numbers are whole numbers or rational numbers.
- Using the area model for multiplication and division can be a fun way for students to understand multiplication and division while also reinforcing math facts.
- To practice multiplication facts, consider using digital and non-digital games instead of flashcards. Game playing is a fun way for students to remember the times tables.
Easy mistakes to make
- Confusing the rules for multiplying and dividing positive and negative numbers
For example, multiplying (-4)\times (-8) and getting a product of -32 instead of 32 .
- Misinterpreting the meaning of key words in word problems resulting in using the incorrect operation
For example, thinking that the word “of” means to divide instead of multiply.
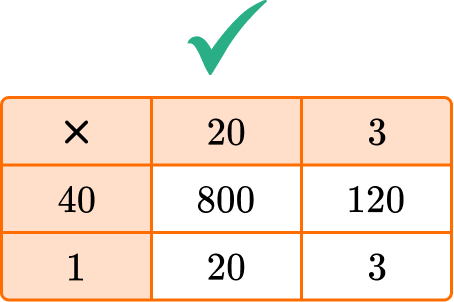
- Confusing place value when using the area model for multiplying multi-digit numbers
For example, when multiplying 23 \times 41 :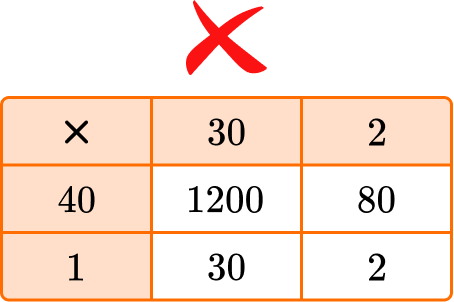
Practice multiplication and division questions
1) Which multiplication expression represents this array?





Count the number of objects in each row.

There are 5 objects in each row which is 5+5.
5+5 is the same as 2 \times 5.
So, 2 \times 5 is the correct expression.
2) Multiply 104 \times 3.




Use the algorithm for multiplying multi-digit numbers, regrouping when necessary.
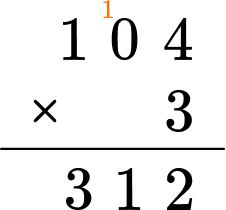
104 \times 3=312
3) Multiply 53 \times 32.




You can use the area model to multiply 53 \times 32.

Add the products together: 1500+100+90+6=1696
53 \times 32=1696
4) Use the array to find the quotient of 16 \div 4 .





Divide the array into 4 equal groups and then count how many objects are in each group.
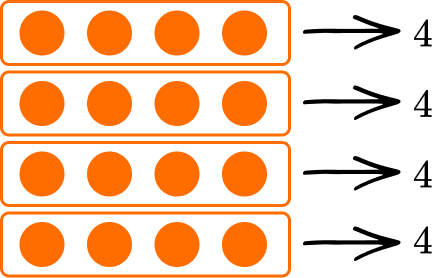
16 \div 4 = 4
5) Divide 128 \div 4.




Divide the numbers using the algorithm for long division.
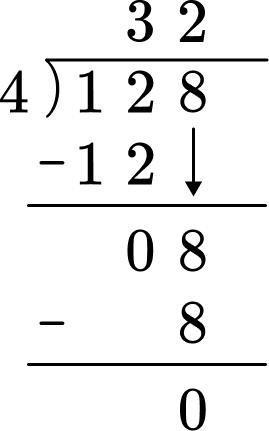
128 \div 4= 32
6) Chris has 3 pencils. Pam has four times as many pencils as Chris. How many pencils does Pam have?
11 pencils

10 pencils

12 pencils

7 pencils

Draw a picture.

4 \times 3=12
Pam has 12 pencils.
Multiplication and division FAQs
Yes, the rules for multiplying and dividing positive and negative numbers hold true regardless if the numbers are whole numbers or rational numbers.
Knowing your multiplication facts and division facts helps when solving problems.
Repeated subtraction is a way for students to begin to develop an understanding of division.
There is not one best strategy to use when multiplying multi-digit numbers. Some strategies, can be quicker than others, but not better.
Knowing your multiplication tables helps to answer questions faster than when you do not know them.
The commutative property of multiplication is: 5 \times 3=3 \times 5 , the order of the numbers does not matter.
The next lessons are
- Types of numbers
- Rounding numbers
- Factors and multiples
- Multiplication and division within 100
Still stuck?
At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.
Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.

Find out how we can help your students achieve success with our math tutoring programs.
[FREE] Common Core Practice Tests (Grades 3 to 6)
Prepare for math tests in your state with these Grade 3 to Grade 6 practice assessments for Common Core and state equivalents.
40 multiple choice questions and detailed answers to support test prep, created by US math experts covering a range of topics!