[FREE] End of Year Math Assessments (Grade 4 and Grade 5)
The assessments cover a range of topics to assess your students' math progress and help prepare them for state assessments.
In order to access this I need to be confident with:
Integers
Absolute value
Adding and subtracting integers
Multiplying and dividing integers
Here you will learn strategies on how to multiply and divide integers, including using visual models as well as using the number line.
Students will first learn about integers in 6th grade math as part of their work with the number system and expand that knowledge to operations with integers in the 7th grade.
What are multiplying and dividing integers?
Multiplying and dividing integers is when you multiply or divide two or more integers together to give a product or quotient that can be either positive or negative.
You can multiply and divide integers using visual models or a rule.
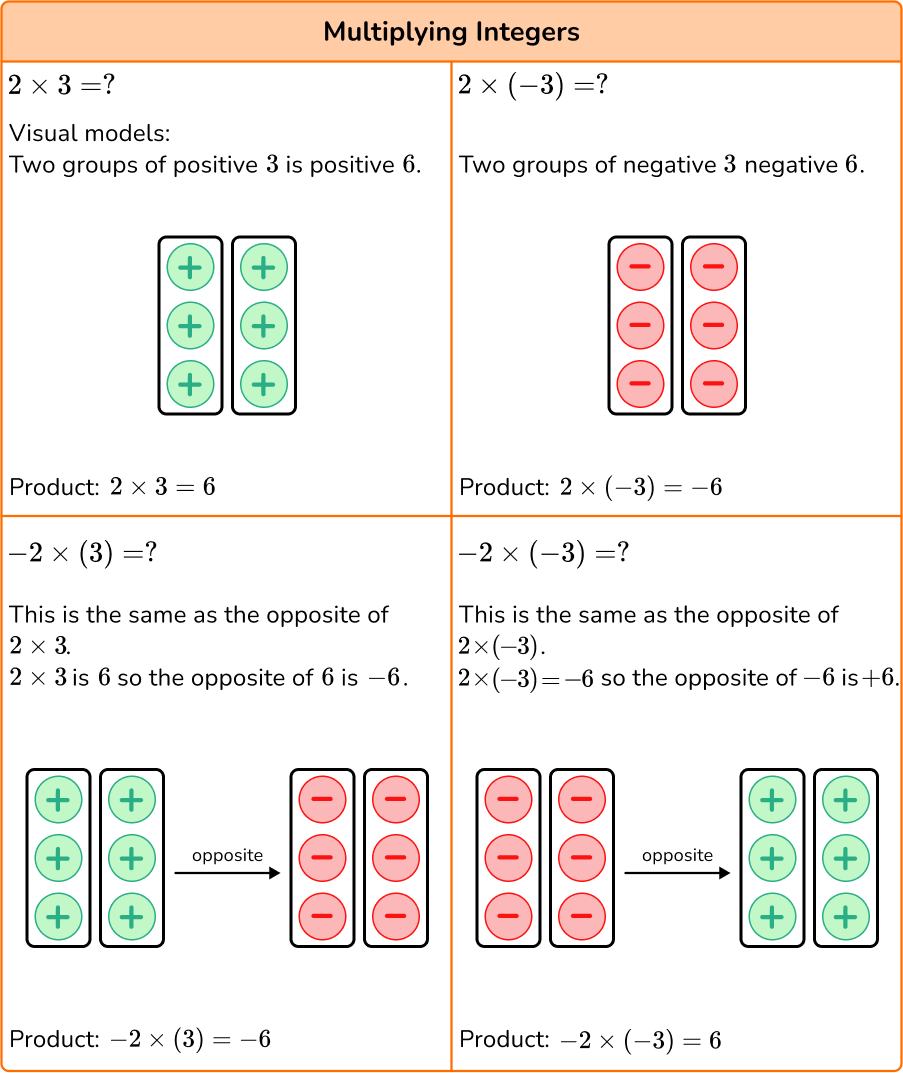
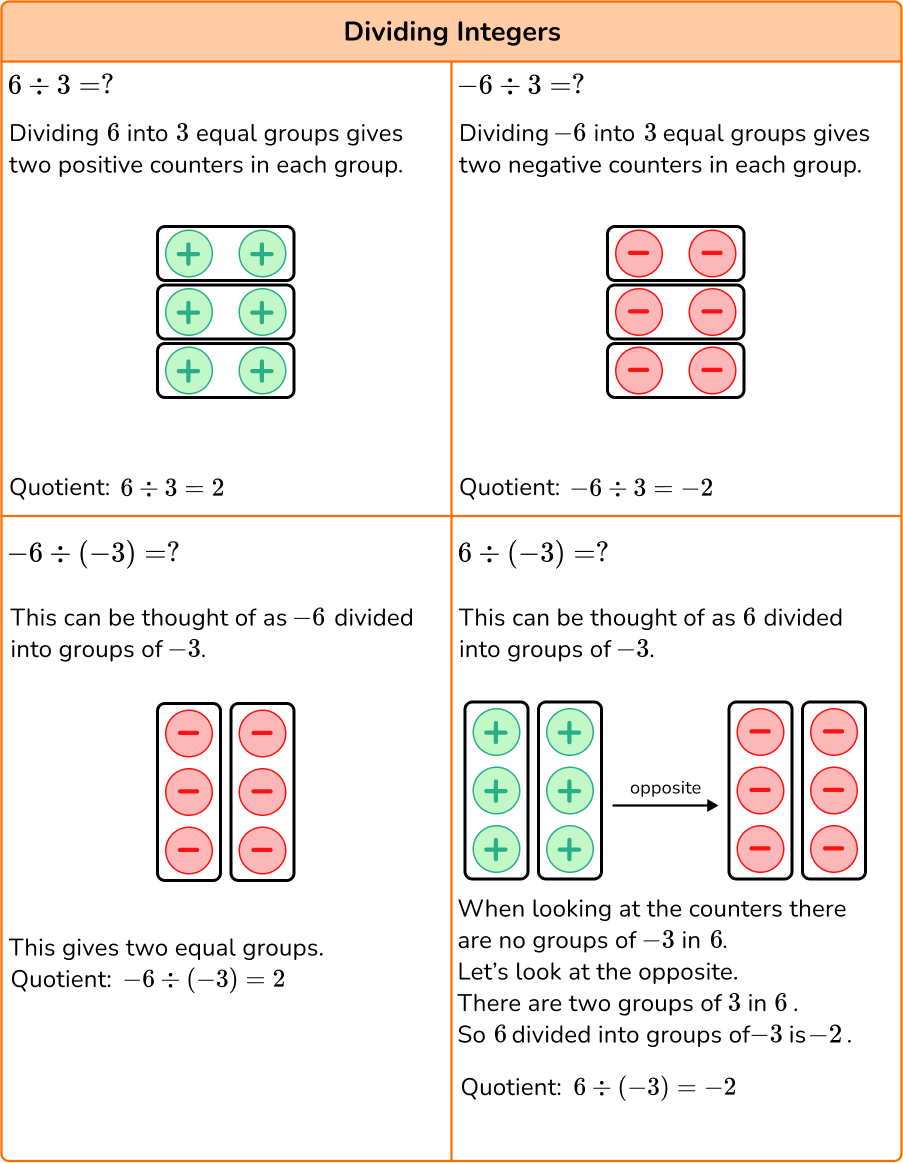
Do you notice a pattern or rule?
Rule for multiplying integers:
- If the integers have the same sign, the product will be positive.
- If the integers have different signs, the product will be negative.
Do you notice a pattern or rule?
Rule for dividing integers:
- If the integers have the same sign, the quotient will be positive.
- If the integers have different signs, the quotient will be negative.
What are multiplying and dividing integers?
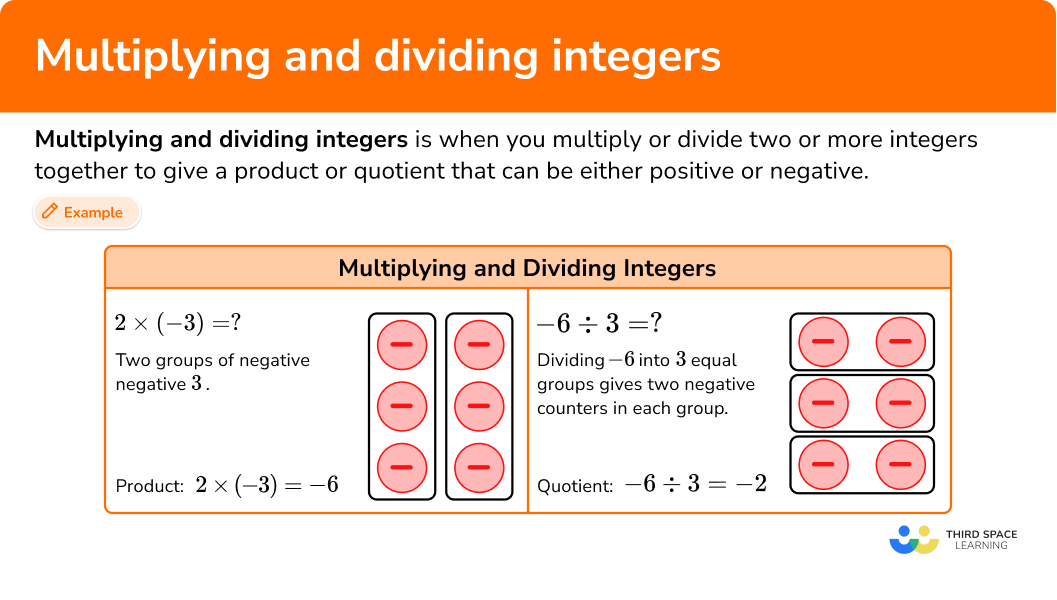
Common Core State Standards
How does this apply to 6th grade math and 7th grade math?
- Grade 6: Number System (6.NS.C.6)
Understand a rational number as a point on the number line. Extend number line diagrams and coordinate axes familiar from previous grades to represent points on the line and in the plane with negative number coordinates.
- Grade 7: Number System (7.NS.A.2)
Apply and extend previous understandings of multiplication and division and of fractions to multiply and divide rational numbers.
How to multiply and divide integers?
In order to add and subtract integers using counters:
- If the integers have the same sign, the product or quotient is positive. If not, go to step 2.
- If the integers have different signs, the product or quotient is negative.
- Find the product or quotient.
![[FREE] End of Year Math Assessments (Grade 4 & Grade 5)](https://thirdspacelearning.com/wp-content/uploads/2023/02/end-of-year-math-assessment-grade-4-grade-5.png)
[FREE] End of Year Math Assessments (Grade 4 & Grade 5)
Assess math progress for the end of grade 4 and grade 5 or prepare for state assessments with these mixed topic, multiple choice questions and extended response questions!
DOWNLOAD FREE [FREE] End of Year Math Assessments (Grade 4 & Grade 5)
Assess math progress for the end of grade 4 and grade 5 or prepare for state assessments with these mixed topic, multiple choice questions and extended response questions!
DOWNLOAD FREEMultiplying and dividing integers examples
Example 1: multiplying integers with the same sign
Multiply: (-4) \times(-12)= \, ?
- If the integers have the same sign, the product or quotient is positive. If they don’t go to step 2.
-4 and -12 have the same sign so the product is positive.
2If the integers have different signs, the product or quotient is negative.
Integers have the same sign.
3Find the product or quotient.
(-4) \times(-12)=48
Example 2: multiplying integers with different signs
Multiply: (-13) \times 8= \, ?
If the integers have the same sign, the product or quotient is positive. If not, go to step 2.
-13 and 8 do not have the same sign.
If the integers have different signs, the product or quotient is negative.
The integers have different signs so the product is negative.
Find the product or the quotient.
(-13) \times 8=-104
Example 3: dividing integers with the same sign
Divide: \cfrac{(-18)}{(-3)}= \, ?
If the integers have the same sign, the product or quotient is positive. If not, go to step 2.
-18 and -3 have the same sign so the quotient will be positive.
If the integers have different signs, the product or quotient is negative.
Integers have the same sign.
Find the product or quotient.
\cfrac{(-18)}{(-3)}=6
Example 4: dividing integers with different signs
Divide: -120 \div 3= \, ?
If the integers have the same sign, the product or quotient is positive. If not, go to step 2.
-120 and 3 do not have the same sign.
If the integers have different signs, the product or quotient is negative.
-120 and 3 have different signs so the quotient will be negative.
Find the product or quotient.
-120 \div 3=-40
Example 5: multiplying integers word problem
From sea level, a submarine descends 25 \, ft. per minute (-25 \, ft.).
After 6 minutes, the submarine’s distance can be modeled by (-25) \times 6 = \, d , where d is the submarine in relation to sea level.
How far below sea level is the submarine?
If the integers have the same sign, the product or quotient is positive. If not, go to step 2.
-25 and 6 do not have the same sign.
If the integers have different signs, the product or quotient is negative.
-25 and 6 have different signs so the product will be negative.
Find the product or quotient.
-25 \times 6=-150
Because the submarine is descending, after 6 minutes it will be 150 feet below sea level.
Example 6: dividing integer word problems
On a certain winter day, the temperature changed at a rate of -4 degrees Fahrenheit per hour.
After a specific amount of time, the change in temperature was -36 degrees Fahrenheit, which is modeled by (-36) \div (-4) = \, h, where h represents the amount of hours.
How long did it take for the change in temperature to be -36 degrees Fahrenheit?
If the integers have the same sign, the product or quotient is positive. If not, go to step 2.
-36 and -4 have the same sign so the quotient is positive.
If the integers have different signs, the product or quotient is negative.
The integers have the same sign.
Find the product or quotient.
(-36) \div(-4)=9
9 hours.
Teaching tips for multiplying and dividing integers
- Multiplying and dividing integers are foundational skills for Algebra 1. Using manipulatives helps students formulate conceptual understanding.
- Have students identify the patterns with multiplying and dividing integers so that they can figure out the rules on their own.
- Although practice integer worksheets have their place, have students practice problems through digital games or scavenger hunts around the room to make it engaging.
- Reinforce essential vocabulary such as dividend, divisor, quotient, factors, and product.
Easy mistakes to make
- Mixing up the rules for multiplication and division.
For example, when multiplying integers with the same sign, you get a negative product, and when dividing integers with the same sign, you get a negative quotient.
- Mixing up the rules of multiplication and division with addition and subtraction.
For example, applying the rule of addition of integers to (15) \div(-3)=5 where the absolute value of 15 is greater than the absolute value of 3 so the answer must be positive.
Related multiplication and division lessons
This multiplying and dividing integers topic guide is part of our series on multiplication and division. You may find it helpful to start with the main multiplication and division topic guide for a summary of what to expect or use the step-by-step guides below for further detail on individual topics. Other topic guides in this series include:
- Multiplication and division
- Multiplying multi-digit numbers
- Understanding multiplication
- Multiplication and division within 100
- Long division
- Multiplying and dividing rational numbers
- Understanding division
- Dividing multi-digit numbers
- Multiplicative comparisons
Practice multiplying and dividing integers
1. Multiply: (6) \times(-2)=\text { ? }
Using the rule for multiplying integers, 6 and -2 have different signs, so the product is negative.
(6) \times(-2)=-12
You can check your answer with counters.
6 groups of -2 counters is -12 counters
2. Multiply: (-15) \times(-3)= \text { ? }
Using the rule for multiplying integers, -15 and -3 have the same sign, so the product is positive.
(-15) \times(-3)=45
3. Divide: (-52) \div(4)= \text { ? }
Using the rule for dividing integers, -52 and 4 have different signs, so the quotient is negative.
(-52) \div(4)=-13
4. Divide: \cfrac{(-72)}{(-9)}= \text { ? }
Using the rule for dividing integers, -72 and -9 have the same sign, so the quotient is positive.
\cfrac{(-72)}{(-9)}=8
5. Multiply: (-190) \times(-10)= \text { ? }
Using the rule for multiplying integers, -190 and -10 have the same sign, so the product is positive.
(-190) \times(-10)=1900
6. A deep sea diver descends at a rate of 10 feet per minute below sea level. The diver descends at this rate for 8 minutes, which can be modeled by 8 \times (-10) = d, where d is how far the diver is below sea level. After 8 minutes, how far did the diver descend?
-80 feet
80 feet
-25 feet
25 feet
Using the rule, the signs of the numbers are different, so the product is negative.
8 \times(-10)=-80
The diver descended to -80 feet.
Multiplying and dividing integers FAQs
Yes, there are negative fractions and decimals. Numbers to the left of 0 on the number line are negative.
Yes, using the number line can also help visualize the product. For example, 2 \times(-3)=-6 and can be represented on the number line: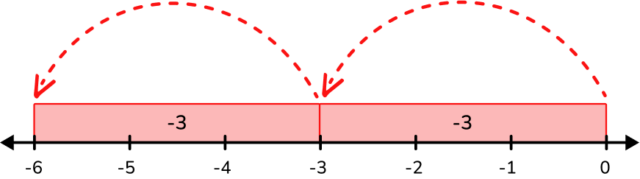
When it comes to sets of numbers, whole numbers are 0 and positive whole numbers. The set of integers includes all negative whole numbers, 0, and all positive whole numbers.
Multiplication and division of integers help when simplifying algebraic expressions and solving equations.
Yes, positive numbers are to the right of 0 and negative numbers are to the left of 0.
The positive sign does not necessarily need to be written in front of a number. For example, +5 is the same as 5. The positive sign is understood.
The next lessons are
- Solving one step equations
- Order of operations
Still stuck?
At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.
Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.
Find out how we can help your students achieve success with our Elementary math tutoring programs.