[FREE] Fun Math Games & Activities Packs
Always on the lookout for fun math games and activities in the classroom? Try our ready-to-go printable packs for students to complete independently or with a partner!
In order to access this I need to be confident with:
Less than sign Greater than sign Multiplying and dividing fractionsNumerator and denominator
Here you will learn about the numerator and denominator of fractions, including equivalent fractions, improper fractions, unit fractions and mixed fractions.
Students will first learn about fractions in 3rd grade math as part of their work in number and operations with fractions and build upon that knowledge as they progress through elementary school.
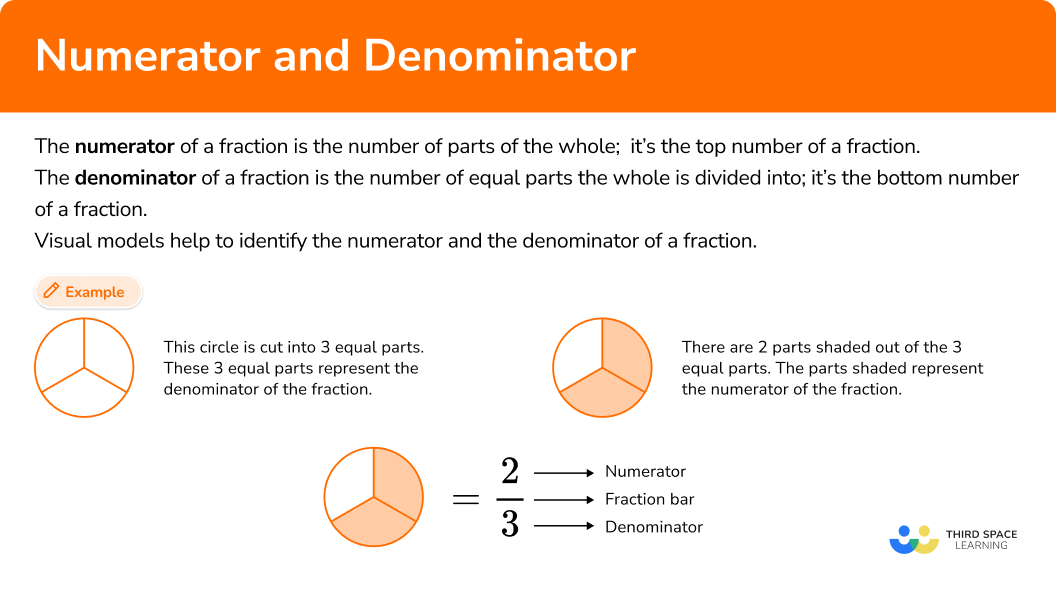
What are the numerator and denominator?
The numerator and denominator of a fraction are the top and bottom numbers of a fraction.
The numerator of a fraction is the number of parts of the whole; it’s the top number of a fraction.
The denominator of a fraction is the number of equal parts the whole is divided into; it’s the bottom number of a fraction.
Visual models help to identify the numerator and the denominator of a fraction.
 | This circle is cut into 3 equal parts.
|
 | There are 2 parts shaded out of the 3
|
 | = \cfrac{2}{3} |
\cfrac{2}{3} \, is a proper fraction because the numerator is less than the denominator.
2 < 3Proper fractions are always less than one.
An improper fraction is one in which the numerator is greater than the denominator. Improper fractions are always greater than 1. They can be written as mixed numbers.
For example, \cfrac{4}{3} \, is an improper fraction because 4 > 3.
3 our of 3 shaded parts which is 1 whole  | 1 our of 3 shaded parts which is \cfrac{1}{3}  |
\cfrac{4}{3} \, is the same as 1\cfrac{1}{3}
A unit fraction is a fraction where the numerator is 1.
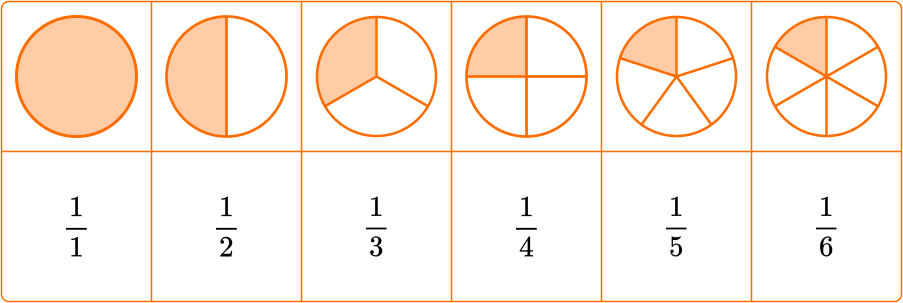
Unit fractions help to decompose (break apart) fractions.
Let’s decompose the fraction \, \cfrac{5}{6} \, into unit fractions.
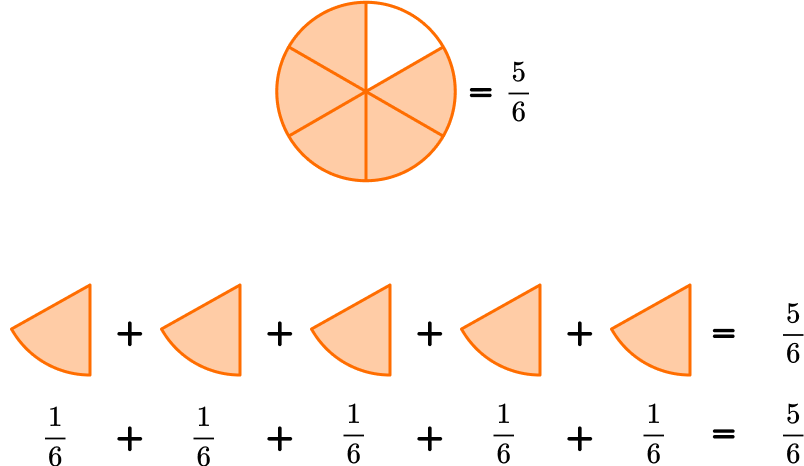
Unit fractions on the number line can also help to decompose a fraction.
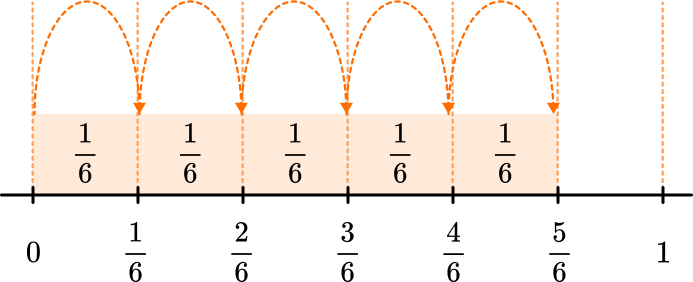
Equivalent fractions are fractions that look different but represent the same value.
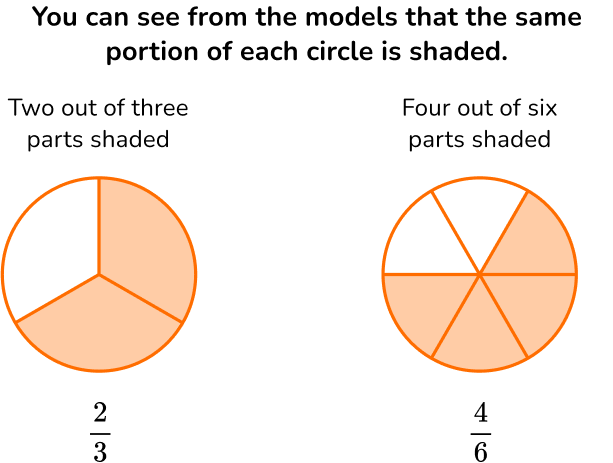
Let’s check to make sure \, \cfrac{2}{3} \, is equivalent to \, \cfrac{4}{6}.
If you multiply the numerator and the denominator of \, \cfrac{2}{3} \, by a common factor of 2 you will get \, \cfrac{4}{6}
\cfrac{2}{3}=\cfrac{2 \; \times \; 2}{3 \; \times \; 2}=\cfrac{4}{6}So, \cfrac{2}{3} = \cfrac{4}{6}
What are the Numerator and Denominator?
![[FREE] Numerator and Denominator Worksheet (Grade 3 and 4)](https://thirdspacelearning.com/wp-content/uploads/2024/01/Numerator-and-Denominator-Worksheet-listing-image.png)
[FREE] Numerator and Denominator Worksheet (Grade 3 and 4)
Use this worksheet to check your grade 3 and 4 students’ understanding of numerator and denominator. 15 questions with answers to identify areas of strength and support!
DOWNLOAD FREE [FREE] Numerator and Denominator Worksheet (Grade 3 and 4)
Use this worksheet to check your grade 3 and 4 students’ understanding of numerator and denominator. 15 questions with answers to identify areas of strength and support!
DOWNLOAD FREECommon Core State Standards
How does this relate to 3rd grade math and 4th grade math?
- Grade 3 – Number and Operations – Fractions (3.NF.A.1)
Understand a fraction \, \cfrac{1}{b} \, as the quantity formed by 1 part when a whole is partitioned into b equal parts; understand a fraction \, \cfrac{a}{b} \, as the quantity formed by a parts of size \, \cfrac{1}{b}.
- Grade 4 – Number and Operations – Fractions (4.NF.A.1)
Explain why a fraction \, \cfrac{a}{b} \, is equivalent to a fraction \, \cfrac{(n \, \times \, a)}{(n \, \times \, b)} \, by using visual fraction models, with attention to how the number and size of the parts differ even though the two fractions themselves are the same size. Use this principle to recognize and generate equivalent fractions.
- Grade 4 – Number and Operations – Fractions (4.NF.B.3.b)
Decompose a fraction into a sum of fractions with the same denominator in more than one way, recording each decomposition by an equation. Justify decompositions, e.g., by using a visual fraction model.
How to use numerators and denominators
In order to write a proper fraction from a visual model:
- Count the equal parts the model is divided to find the denominator.
- Count how many shaded parts there are to find the numerator.
- Write the fraction with the numerator on top and the denominator on the bottom.
In order to write an improper fraction from a model and make it a mixed number:
- Count how many equal parts the model is divided into in order to find the denominator.
- Count how many total parts are shaded; identify the wholes and the fractional part.
- Write the mixed number with the whole number first, then the fraction part with the numerator on top and the denominator on the bottom.
- Write the mixed number.
In order to determine a unit fraction:
- Count how many equal parts the model or shape is divided into in order to find the denominator.
- Write the unit fraction to represent one part.
In order to decompose fractions into unit fractions using a visual model:
- Count how many equal parts the model is divided into in order to find the denominator.
- Count how many shaded parts there are in order to find the numerator.
- Write the fraction.
- Look at Step 2, the number of shaded parts is the number of unit fractions.
- Write the unit fraction as an addition statement.
In order determine if the given fractions are equivalent using a model:
- Look to see if the shaded area is approximately the same.
- Compare the numerators and denominators of the given fractions.
- Using either multiplication or division, find the common factor that was multiplied or divided from the first fraction to the second fraction.
- Write the equivalent fractions.
Numerator and denominator examples
Example 1: writing a proper fraction from a visual model
Write the fraction that is represented by the model.
- Count how many equal parts the model is divided into in order to find the denominator.
The model is divided into 5 equal parts so the denominator is 5.
2Count how many shaded parts there are in order to find the numerator.
There are 3 shaded parts so the numerator is 3.
3Write the fraction with the numerator on top and the denominator on the bottom.
The model represents \, \cfrac{3}{5} .
Example 2: writing an improper fraction from a model
Write the fraction that is represented by the model.
Count how many equal parts the models are divided into in order to find the denominator.
Each model is divided into 3 equal parts. So the denominator is 3.
Count how many total parts are shaded; identify the wholes and the fractional part.
One model has 3 out of 3 shaded parts which represents the 1 whole.
The second model has 2 out of 3 models shaded which represents the fractional part.
Write the mixed number with the whole number first, then the fraction part with the numerator on top and the denominator on the bottom.
\cfrac{3}{3}=1 plus \cfrac{2}{3}
2 is the numerator because it’s the shaded part in the second circle and 3 is the denominator because that’s how many equal parts the circle is divided into.
Write the mixed number.
1+ \cfrac{2}{3}=1 \cfrac{2}{3}
Example 3: writing a unit fraction
Mary divided a circle into 4 equal pieces. What would be the unit fraction representing 1 part?
Count how many equal parts the model or shape is divided into in order to find the denominator.
Mary divided a circle into 4 equal pieces. This is a model of her circle.
Write the unit fraction to represent one part.
1 part shaded out of 4 represents the unit fraction. The unit fraction is \cfrac{1}{4} .
Example 4: decompose a fraction into unit fractions
Express \, \cfrac{3}{8} \, as the sum of unit fractions.
Count how many equal parts the model or shape is divided into in order to find the denominator.
The circle is divided into 8 equal parts so the denominator is 8.
Count how many shaded parts there are in order to find the numerator.
There are 3 parts shaded, so the numerator is 3. Each part shaded represents \cfrac{1}{8} of the circle.
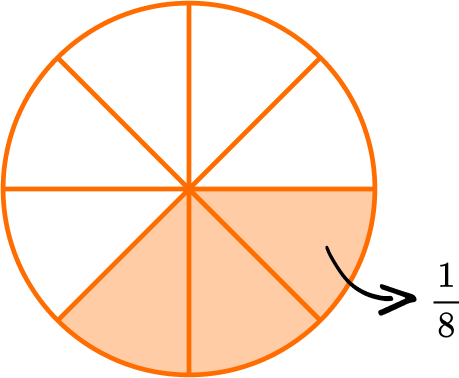
Write the unit fraction to represent \bf{1} part.
The unit fraction would be 1 part of the 8 parts, so it is \cfrac{1}{8} .
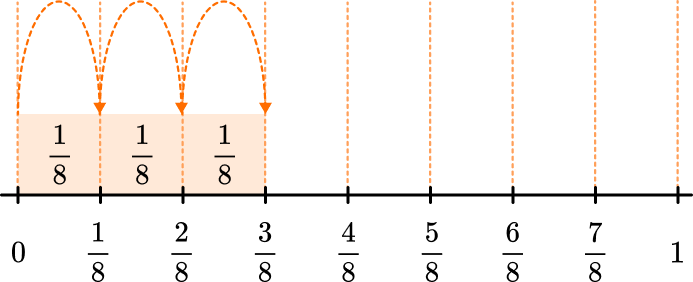
Break apart the fraction into the sum of unit fractions.
\cfrac{1}{8}+ \cfrac{1}{8}+ \cfrac{1}{8}= \cfrac{3}{8}
Example 5: equivalent fractions
Write the equivalent fractions represented in the models.
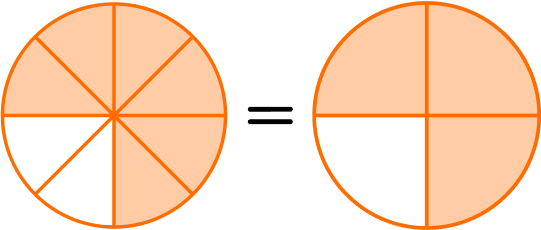
Look to see if approximately the same area is shaded.
It looks like approximately the same area of both circles is shaded.
Compare the numerators and denominators of the given fractions.
The first model is divided into 8 equal parts with 6 parts shaded. \cfrac{6}{8}
The second model is divided into 4 equal parts with 3 parts shaded. \cfrac{3}{4}
Using either multiplication or division, find the common factor that was multiplied or divided from the first fraction to the second fraction.
Using division, the common factor is 2.
\cfrac{6}{8}=\cfrac{6 \, \div \, 2}{8 \, \div \, 2}=\cfrac{3}{4}
Write the equivalent fractions.
\cfrac{6}{8}=\cfrac{3}{4}
Example 6: equivalent fractions
Determine if the fractions represented in the models are equivalent.
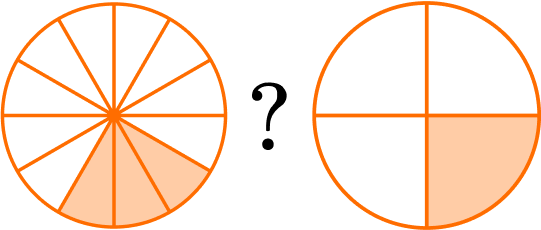
Look to see if approximately the same area is shaded.
It appears as though approximately the same portion of the circles are shaded.
Compare the numerators and denominators of the given fractions.
The first model is divided into 12 equal parts with 3 parts shaded. \cfrac{3}{12}
The second model is divided into 4 equal parts with 1 part shaded. \cfrac{1}{4}
Using either multiplication or division, find the common factor that was multiplied or divided from the first fraction to the second fraction.
Using division, the common factor is 3.
\cfrac{3}{12}=\cfrac{3\div 3}{12\div 3}=\cfrac{1}{4}
Write the equivalent fractions.
\cfrac{3}{12}=\cfrac{1}{4}
Teaching tips for numerators and denominators
- Reinforcing the fraction concepts with models and number lines helps students to build number sense.
- Unit fractions can help students understand the value of the fractions. For example, students know that 5 is greater than 2. However, with a fraction \, \cfrac{1}{5} \, is less than \, \cfrac{1}{2} \, which can confuse students. Using a visual model to show unit fractions helps students formulate understanding.
- Consider alternatives to worksheets when practicing skills such as game playing.
- Building understanding through visual models of equivalent fractions leads to deeper understanding of finding common denominators as opposed to just regurgitating a process.
Easy mistakes to make
- Confusing the denominator of the fraction and the numerator of the fraction
For example, thinking that the equal parts a model is divided into represents the numerator instead of the denominator.
- Thinking fractions with different numerators and denominators can’t be equal
For example, \, \cfrac{1}{2} \, and \, \cfrac{3}{6} \, are equal in value because they both represent one-half.
Visually, you can see that they both are the same shaded area.
- Thinking that the fraction \, \cfrac{1}{4} \, is greater than \, \cfrac{1}{2} \,
Students know that 4 is greater than 2, so they can get confused with unit fractions. The more parts a whole is divided into, the smaller the unit fraction’s value.
- Forgetting to multiply or divide the entire fraction by the common factor when finding equivalent fractions
For example, when finding an equivalent fraction to \cfrac{2}{3}, the 2 and the 3 have to be multiplied by the common factor.
Practice numerator and denominator problems
1. What is the fraction represented by the shaded area?
The model is divided into 10 equal parts, with 7 parts shaded.
The denominator is 10 and the numerator is 7.
The numerator is the top number, and the denominator is the bottom number.
\cfrac{7}{10}
2. What is the improper fraction represented by the shaded area?
Each circle is divided into 8 equal parts, so 8 is the denominator.
The first circle has 8 out of 8 parts shaded.
The second circle has 5 out of 8 parts shaded. 8 + 5 = 13, which is the numerator.
The improper fraction is \cfrac{13}{8}
3. What is the mixed number represented by the shaded areas?
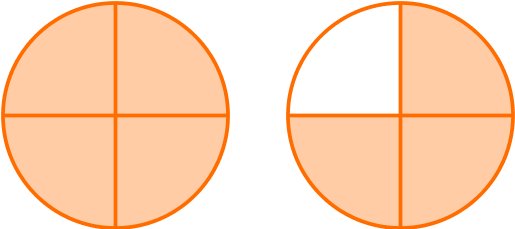
Both models are divided into 4 equal parts so the denominator is 4.
The first circle has 4 out 4 parts shaded which is \cfrac{4}{4}=1.
The second circle has 3 out of 4 parts shaded which is \cfrac{3}{4}.
1 + \cfrac{3}{4}=1\cfrac{3}{4}
4. Express the fraction represented below as the sum of unit fractions.
7 parts are shaded out of 8 equal parts, so the fraction is \cfrac{7}{8}
The unit fraction would be 1 part out of 8 parts, so it is \cfrac{1}{8}
\cfrac{7}{8} = \cfrac{1}{8}+ \cfrac{1}{8}+\cfrac{1}{8}+\cfrac{1}{8}+\cfrac{1}{8}+ \cfrac{1}{8}+\cfrac{1}{8}
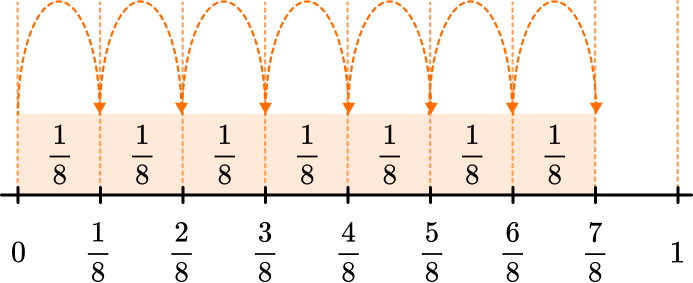
5. Which pair of equivalent fractions represents the circle models?
12 out of 16 parts are shaded in the first circle model, which is \cfrac{12}{16}.
3 out of 4 parts are shaded in the second circle model, which is \cfrac{3}{4}.
Using division, the common factor is 4.
\cfrac{12 \, \div \, 4}{16 \, \div \, 4}=\cfrac{3}{4}
\cfrac{12}{16}=\cfrac{3}{4}
6. Which pair of equivalent fractions represents the circle models?
The first circle model has 2 shaded parts out of 5 parts, \cfrac{2}{6}.
The second circle model has 4 shaded parts out of 10 parts, \cfrac{4}{10}.
Using multiplication, the common factor is 2.
\cfrac{2 \, \times \, 2}{5 \, \times \, 2}=\cfrac{4}{10}
\cfrac{2}{5}=\cfrac{4}{10}
Numerator and denominator FAQs
The denominator tells you how many parts the whole is broken into and is the bottom part of the fraction.
The numerator tells you how many parts of a whole and is the top part of a fraction.
For example, looking at the model:
The whole is divided into 5 equal pieces and 3 pieces are shaded, representing the fraction \cfrac{3}{5} .
The unit fraction can help break apart fractions easily. Unit fractions also help to understand the value of fractions. For example, the unit fraction of \, \cfrac{1}{4} \, is greater than the unit fraction \, \cfrac{1}{8}.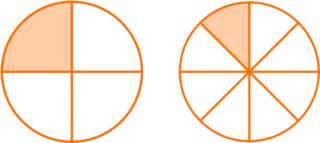 
From the model, you can see that 1 part of 4 is bigger than 1 part of 8.
No, the numerator can be less than the denominator or greater than the denominator. When the numerator of a fraction is less than the denominator, it is a fraction less than 1, called a proper fraction. When the numerator of a fraction is greater than the denominator, it is greater than 1, called an improper fraction.
Yes, a fraction can be seen as division where the numerator is dividend and the denominator is the divisor.
\cfrac{1}{4} → fraction bar represents division
\cfrac{1}{4} \, is 1 \div 4
Still stuck?
At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.
Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.
Find out how we can help your students achieve success with our math tutoring programs.
[FREE] Common Core Practice Tests (Grades 3 to 6)
Prepare for math tests in your state with these Grade 3 to Grade 6 practice assessments for Common Core and state equivalents.
40 multiple choice questions and detailed answers to support test prep, created by US math experts covering a range of topics!