[FREE] Fun Math Games & Activities Packs
Always on the lookout for fun math games and activities in the classroom? Try our ready-to-go printable packs for students to complete independently or with a partner!
Ordering fractions
Here you will learn about ordering fractions from least to greatest and greatest to least.
Students will first learn about ordering fractions as part of numbers and operations of fractions in 4th grade.
What is ordering fractions?
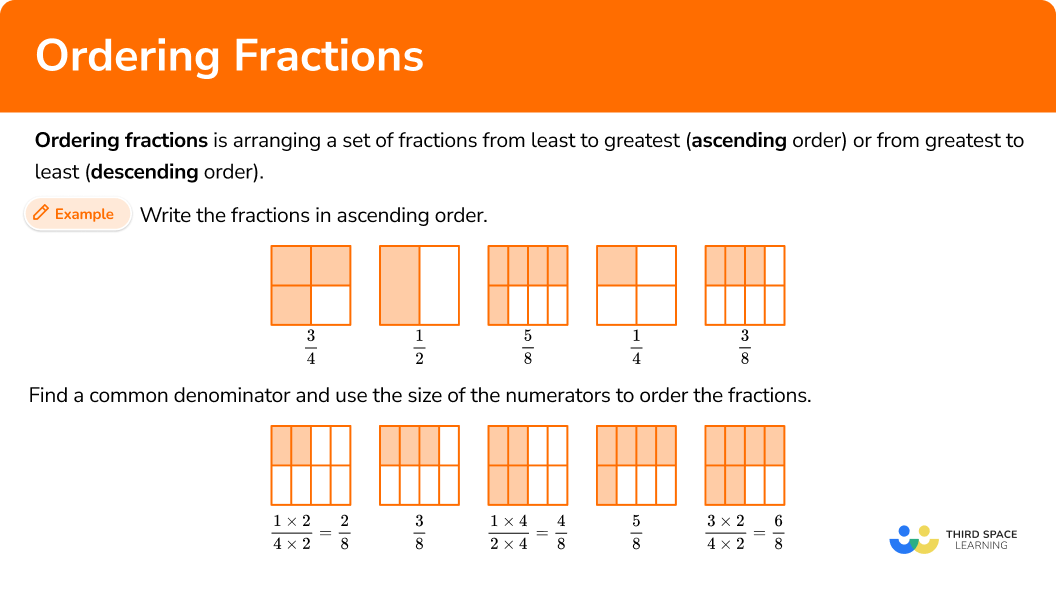
Ordering fractions is arranging a set of fractions from least to greatest (ascending order) or from greatest to least (descending order).
To do this you rewrite the fractions so that they have common denominators and then compare the numerators.
For example,
If you order these fractions from least to greatest…
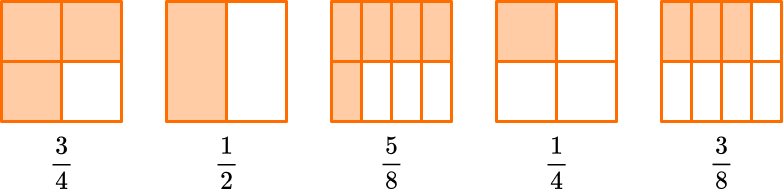
The order becomes…
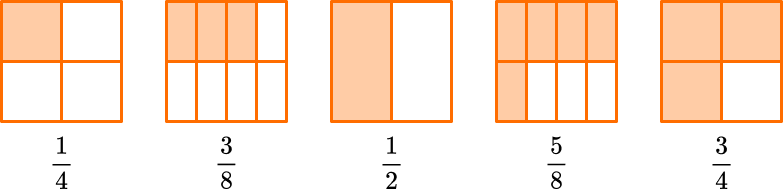
You can prove this order is correct by creating common denominators. All the denominators (2, 4 and 8) have a common multiple of 8, so you can use 8 as the common denominator.
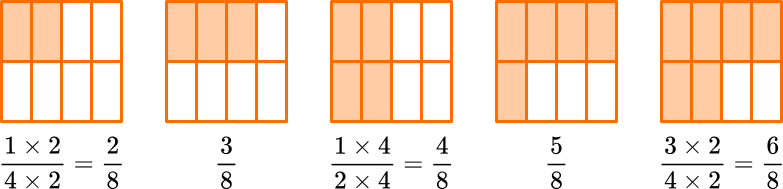
Now the equivalent fractions are: \; \cfrac{2}{8}, \cfrac{3}{8}, \cfrac{4}{8}, \cfrac{5}{8}, \cfrac{6}{8}.
Since the fractions have the same denominators all the parts are the same size. You can use the size of the numerators to order the fractions. The fractions are in order from least to greatest, because the numerators are in order from least to greatest.
What is ordering fractions?
Common Core State Standards
How does this relate to 4th grade math?
- Grade 4: Numbers and Operations – Fractions (4.NF.A.2)
Compare two fractions with different numerators and different denominators, e.g., by creating common denominators or numerators, or by comparing to a benchmark fraction such as \cfrac{1}{2}. Recognize that comparisons are valid only when the two fractions refer to the same whole. Record the results of comparisons with symbols >, =, or <, and justify the conclusions, e.g., by using a visual fraction model.
How to order fractions
In order to order fractions:
- Create equivalent fractions that have a common denominator.
- Order the fractions by the size of the numerator.
- Rewrite the fractions in their original form.
In order to order mixed numbers:
- Convert mixed numbers to improper fractions.
- Create equivalent fractions that have a common denominator.
- Order the fractions by the size of the numerator.
- Rewrite the fractions in their original form.
![[FREE] Ordering Fractions Worksheet (Grade 4 to 5)](https://thirdspacelearning.com/wp-content/uploads/2023/11/Ordering-Fractions-Worksheet-listing-image.png)
[FREE] Ordering Fractions Worksheet (Grade 4 to 5)
![[FREE] Ordering Fractions Worksheet (Grade 4 to 5)](https://thirdspacelearning.com/wp-content/uploads/2023/11/Ordering-Fractions-Worksheet-listing-image.png)
Use this worksheet to check your grade 4 to 5 students’ understanding of ordering fractions. 15 questions with answers to identify areas of strength and support!
DOWNLOAD FREE![[FREE] Ordering Fractions Worksheet (Grade 4 to 5)](https://thirdspacelearning.com/wp-content/uploads/2023/11/Ordering-Fractions-Worksheet-listing-image.png)
[FREE] Ordering Fractions Worksheet (Grade 4 to 5)
![[FREE] Ordering Fractions Worksheet (Grade 4 to 5)](https://thirdspacelearning.com/wp-content/uploads/2023/11/Ordering-Fractions-Worksheet-listing-image.png)
Use this worksheet to check your grade 4 to 5 students’ understanding of ordering fractions. 15 questions with answers to identify areas of strength and support!
DOWNLOAD FREEOrdering fractions examples
Example 1: ordering proper fractions
Order the fractions from least to greatest.

- Create equivalent fractions that have a common denominator.
All the denominators (2, 4, 6 and 12) have a multiple of 12, so you can use 12 as the common denominator.
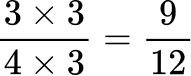
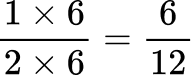
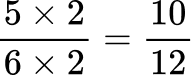
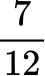
2Order the fractions by the size of the numerator.
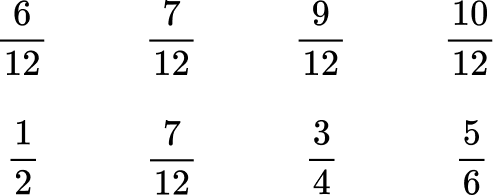
Here are the equivalent fractions with the common denominator of 12 :

Now that the denominators are like, you can order them from least to greatest by the numerator:

3Rewrite the fractions in their original form.
Example 2: ordering proper fractions
Order the fractions from greatest to least.

Create equivalent fractions that have a common denominator.
All the denominators (3, 4, 6 and 8) have a multiple of 24, so you can use 24 as the common denominator.
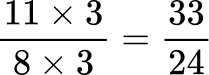
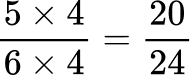
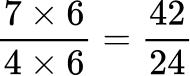
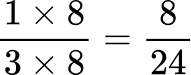
Order the fractions by the size of the numerator.
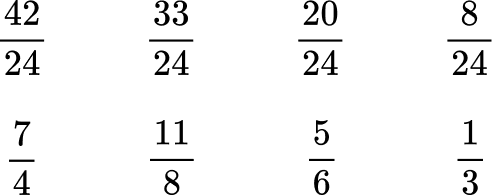
Here are the equivalent fractions with the common denominator of 24 :

Now that the denominators are like, you can order them from greatest to least by the numerator:

Rewrite the fractions in their original form.
Example 3: ordering improper fractions and mixed numbers
Order the numbers from greatest to least.

Convert mixed numbers to improper fractions.
You can write all the numbers as fractions (proper and improper) or as mixed numbers. To use the same steps as above, write them all as fractions.
For 1\cfrac{1}{2}, break the whole into halves, then count the total halves.

There are 3 halves, so 1 \cfrac{1}{2} = \cfrac{3}{2}.
For 1 \cfrac{2}{3}, break the whole into thirds, then count the total thirds.

There are 5 thirds, so 1 \cfrac{2}{3} = \cfrac{5}{3}.
Create equivalent fractions that have a common denominator.
All the denominators (2, 3, 5 and 10) have a multiple of 30, so you can use 30 as the common denominator.
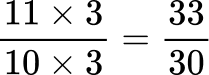
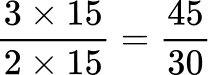
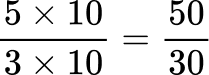
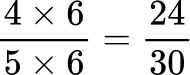
Order the fractions by the size of the numerator.
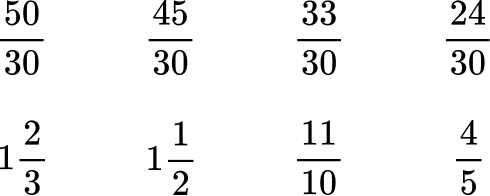
Here are the equivalent fractions with the common denominator of 30 :

Now that the denominators are like, you can order them from greatest to least by the numerator:

Rewrite the fractions in their original form.
Example 4: ordering improper fractions and mixed numbers
Order the numbers from least to greatest.
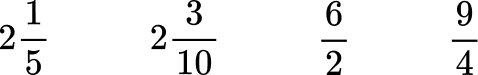
Convert mixed numbers to improper fractions.
You can write all the numbers as fractions (proper and improper) or as mixed numbers. To use the same steps as above, write them all as fractions.
For 2 \cfrac{1}{5}, break the wholes into fifths, then count the total fifths.

There are 11 fifths, so 2 \cfrac{1}{5} = \cfrac{11}{5}.
For 2 \cfrac{3}{10}, break the whole into tenths, then count the total tenths.

There are 23 tenths, so 2 \cfrac{3}{10} = \cfrac{23}{10}.
Create equivalent fractions that have a common denominator.
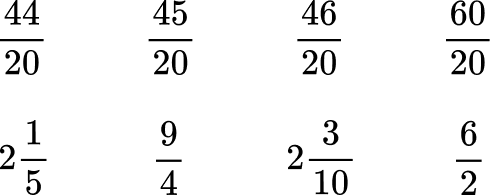
All the denominators (2, 4, 5 and 10) have a common multiple of 20, so you can use 20 as the common denominator.
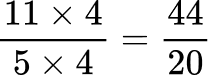
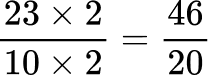
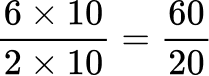
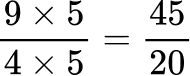
Order the fractions by the size of the numerator.
Here are the equivalent fractions with the common denominator of 20 :

Now that the denominators are like, you can order them from least to greatest by the numerator:

Rewrite the fractions in their original form.
Example 5: ordering improper fractions and mixed numbers
Order the numbers from greatest to least.

Convert mixed numbers to improper fractions.
You can write all the numbers as fractions (proper and improper) or as mixed numbers. To use the same steps as above, write them all as fractions.
For 1\cfrac{1}{3}, break the whole into thirds, then count the total thirds.

There are 4 thirds, so 1\cfrac{1}{3} = \cfrac{4}{3}.
For 1\cfrac{1}{2}, break the whole into halves, then count the total halves.

There are 3 halves, so 1\cfrac{1}{2} = \cfrac{3}{2}.
Create equivalent fractions that have a common denominator.
All the denominators (2, 3, 6 and 9) have a common multiple of 18, so you can use 18 as the common denominator.
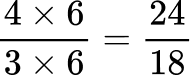
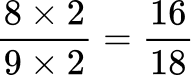
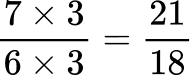
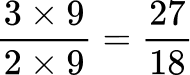
Order the fractions by the size of the numerator.
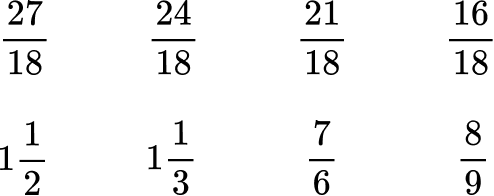
Here are the equivalent fractions with the common denominator of 18 :

Now that the denominators are like, you can order them from greatest to least by the numerator:

Rewrite the fractions in their original form.
Teaching tips for ordering fractions
- Before ordering multiple fractions, students should be comfortable comparing two fractions. Comparing fractions can be done through common numerators, common denominators or with benchmark fractions. Although not modeled here, these strategies can also be used for ordering fractions.
- Fraction work in 3rd grade centers around understanding through models; particularly area models and number lines. To build on this in 4th grade, always have physical or digital models available for students to use when necessary.
- While ordering fractions worksheets have their place, look for ways to incorporate real world activities as practice as well. For example, students can order the ingredients of a recipe or they can measure multiple items in inches and then order the measurements.
Our favorite mistakes
- Assuming that an improper fraction is smaller than a mixed number
Both improper fractions and mixed numbers have wholes, they are just represented in different ways. Improper fractions include wholes as part of the numerator, so it is not always as obvious how many wholes there are. Because of this it can be easy to think that a mixed number is greater, but that is not always true.
For example,
\cfrac{8}{3} is larger than 2 \cfrac{1}{3}, because \cfrac{8}{3} = 2 \cfrac{2}{3}.
- Assuming the fraction with the smallest numbers is the smallest fraction
It is the relationship between the numerator and denominator that matters, not just thinking about the numbers individually.
For example,
\cfrac{3}{4} may seem smaller than \cfrac{68}{100}, since 3 and 4 are smaller numbers, but if you use a common denominator to compare them, you see that \cfrac{3}{4} is the larger fraction:
\cfrac{3 \; \times \; 25}{4 \; \times \; 25}=\cfrac{75}{100} \; and \; \cfrac{75}{100}>\cfrac{68}{100}.
- Mixing up the order
Pay attention to whether the order should be least to greatest or greatest to least. It is easy to confuse the two and often multiple choice tests have both orders listed as answers, but the correct answer is the order that was asked in the question.
- Not recording the answer as the original fractions
It is easy to do the work and then forget to write the original numbers as your final answer.
For example,
Write these numbers in order of size:
\cfrac{5}{6} \quad \cfrac{7}{12} \quad \cfrac{3}{4}
With the same denominator:
\cfrac{10}{12} \quad \cfrac{7}{12} \quad \cfrac{9}{12}
In order of size:
\cfrac{7}{12} \quad \cfrac{9}{12} \quad \cfrac{10}{12}
The final answer is:
\cfrac{7}{12} \quad \cfrac{3}{4} \quad \cfrac{5}{6}
Practice ordering fractions questions
1. Order the fractions from least to greatest.





All the denominators (2, 3, 6 and 12) have a multiple of 12, so you can use 12 as the common denominator.
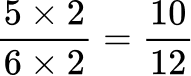
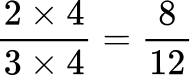
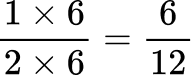
![]()
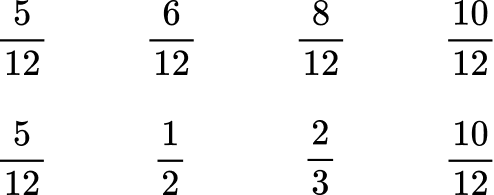
Here are the equivalent fractions with the common denominator of 12 :
![]()
Now that the denominators are like, you can order them from least to greatest by the numerator:
![]()
Rewrite the fractions in their original form.
2. Order the fractions from greatest to least.





All the denominators (4, 6, 8 and 12) have a common multiple of 24, so you can use 24 as the common denominator.
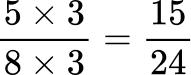
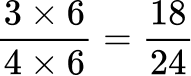
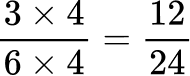
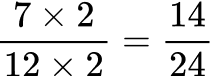
Here are the equivalent fractions with the common denominator of 24 :
![]()
Now that the denominators are like, you can order them from greatest to least by the numerator:
![]()
Rewrite the fractions in their original form.
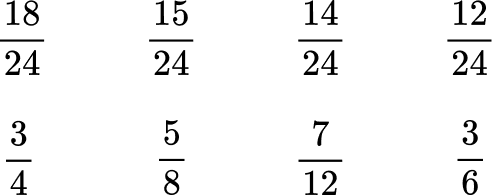
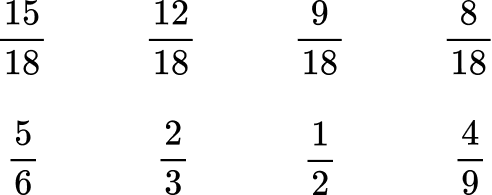
3. Order the fractions from greatest to least.





All the denominators (2, 3, 6 and 9) have a multiple of 18, so you can use 18 as the common denominator.
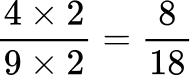
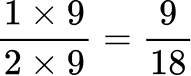
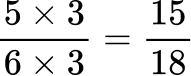
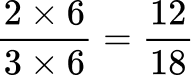
Here are the equivalent fractions with the common denominator of 18 :
![]()
Now that the denominators are like, you can order them from greatest to least by the numerator:
![]()
Rewrite the fractions in their original form.
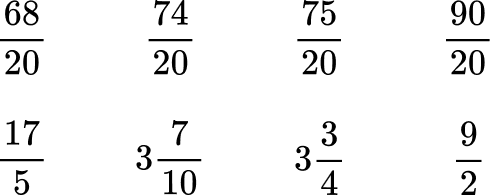
4. Order the numbers from least to greatest.
![]()




You can write all the numbers as fractions (proper and improper) or as mixed numbers. To use the same steps as above, write them all as fractions.
For 3\cfrac{7}{10}, break the wholes into tenths, then count the total tenths.

There are 37 tenths, so 3\cfrac{7}{10} = \cfrac{37}{10}.
For 3\cfrac{3}{4}, break the wholes into fourths, then count the total fourths.
There are 15 fourths, so 3\cfrac{3}{4} = \cfrac{15}{4}.
All the denominators (2, 4, 5 and 10) have a common multiple of 20, so you can use 20 as the common denominator.
![]()
![]()
![]()
![]()
Here are the equivalent fractions with the common denominator of 20 :

Now that the denominators are like, you can order them from least to greatest by the numerator:
![]()
Rewrite the fractions in their original form.
5. Order the numbers from least to greatest.
![]()




You can write all the numbers as fractions (proper and improper) or as mixed numbers. To use the same steps as above, write them all as fractions.
For 4\cfrac{1}{3}, break the wholes into thirds, then count the total thirds.

There are 13 thirds, so 4\cfrac{1}{3} = \cfrac{13}{3}.
For 4\cfrac{2}{5}, break the wholes into fifths, then count the total fifths.

There are 22 fifths, so 4\cfrac{2}{5} = \cfrac{22}{5}.
All the denominators (2, 3, 5 and 10) have a multiple of 30, so you can use 30 as the common denominator.
![]()
![]()
![]()
![]()
Here are the equivalent fractions with the common denominator of 30 :
![]()
Now that the denominators are like, you can order them from least to greatest by the numerator:
![]()
Rewrite the fractions in their original form.
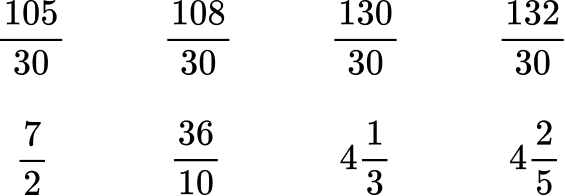
6. Order the numbers from greatest to least.
![]()




You can write all the numbers as fractions (proper and improper) or as mixed numbers. To use the same steps as above, write them all as fractions.
For 2\cfrac{5}{12}, break the wholes into twelfths, then count the total twelfths.

There are 29 twelfths, so 2\cfrac{5}{12} = \cfrac{29}{12}.
For 2\cfrac{2}{3}, break the wholes into thirds, then count the total thirds.

There are 8 thirds, so 2\cfrac{2}{3} = \cfrac{8}{3}.
All the denominators (3, 5, 6 and 12) have a common multiple of 60, so you can use 60 as the common denominator.
![]()
![]()
![]()
![]()
Here are the equivalent fractions with the common denominator of 60 :
![]()
Now that the denominators are like, you can order them from greatest to least by the numerator:
![]()
Rewrite the fractions in their original form.
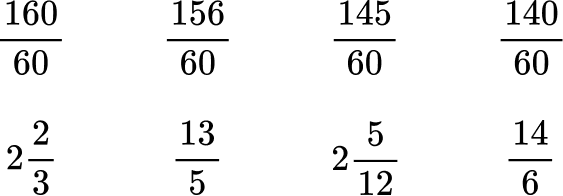
Ordering fractions FAQs
No, any other comparison strategy (like common numerators or using benchmark fractions) can be used with ordering. However, with four or more fractions, many people find it easiest to use common denominators to compare.
No, any common denominator can be used to order fractions, but using the least common denominator makes the calculations simpler.
While listing numbers is more common in elementary school, the comparison symbols can also be used to show order. For example, you could write the answer to #6 as 2 \cfrac{2}{3}>\cfrac{13}{5}>2 \cfrac{5}{12}>\cfrac{14}{6}.
Yes, but just as comparing fractions and mixed numbers requires some conversions other types of numbers may require conversions as well. It is important that you are seeing or thinking about numbers in the same form before comparing.
The next lessons are
Still stuck?
At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.
Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.

Find out how we can help your students achieve success with our math tutoring programs.
[FREE] Common Core Practice Tests (Grades 3 to 6)
Prepare for math tests in your state with these Grade 3 to Grade 6 practice assessments for Common Core and state equivalents.
40 multiple choice questions and detailed answers to support test prep, created by US math experts covering a range of topics!