[FREE] Fun Math Games & Activities Packs
Always on the lookout for fun math games and activities in the classroom? Try our ready-to-go printable packs for students to complete independently or with a partner!
In order to access this I need to be confident with:
Whole numbers Addition and subtraction Multiplication and division Prime and composite numbersFractions operations
Here you will learn about fractions operations, including how to add, subtract, multiply and divide with fractions.
Students will first learn about fractions operations as part of number and operations in fractions in elementary school. They will continue to build on this knowledge in the number system in 6th grade and 7th grade.
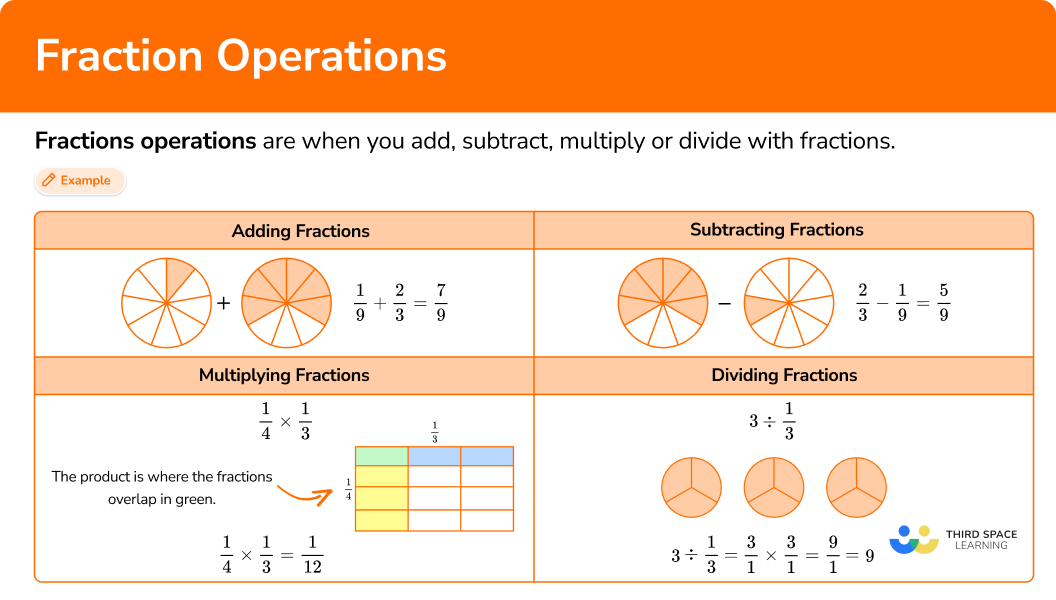
What are fractions operations?
Fractions operations are when you add, subtract, multiply or divide with fractions.
For example,
![[FREE] Fraction Operations Worksheet (Grade 4 to 6)](https://thirdspacelearning.com/wp-content/uploads/2023/07/Fraction-operations-check-for-understandin-quiz-listing-image-.png)
[FREE] Fraction Operations Worksheet (Grade 4 to 6)
![[FREE] Fraction Operations Worksheet (Grade 4 to 6)](https://thirdspacelearning.com/wp-content/uploads/2023/07/Fraction-operations-check-for-understandin-quiz-listing-image-.png)
Use this quiz to check your grade 4 to 6 students’ understanding of fraction operations. 10+ questions with answers covering a range of 4th to 6th grade fraction operations topics to identify areas of strength and support!
DOWNLOAD FREE![[FREE] Fraction Operations Worksheet (Grade 4 to 6)](https://thirdspacelearning.com/wp-content/uploads/2023/07/Fraction-operations-check-for-understandin-quiz-listing-image-.png)
[FREE] Fraction Operations Worksheet (Grade 4 to 6)
![[FREE] Fraction Operations Worksheet (Grade 4 to 6)](https://thirdspacelearning.com/wp-content/uploads/2023/07/Fraction-operations-check-for-understandin-quiz-listing-image-.png)
Use this quiz to check your grade 4 to 6 students’ understanding of fraction operations. 10+ questions with answers covering a range of 4th to 6th grade fraction operations topics to identify areas of strength and support!
DOWNLOAD FREEAdding and subtracting fractions
Adding and subtracting fractions means finding the sum or the difference of two or more fractions.
In order to do this, the fractions must have a common denominator (bottom number).
The numerator shows the number of parts out of the whole and the denominator shows how many equal parts the whole is divided into.
To add or subtract the numerators (top numbers) and keep the denominators the same.
For example,
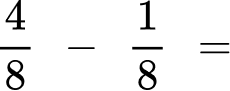
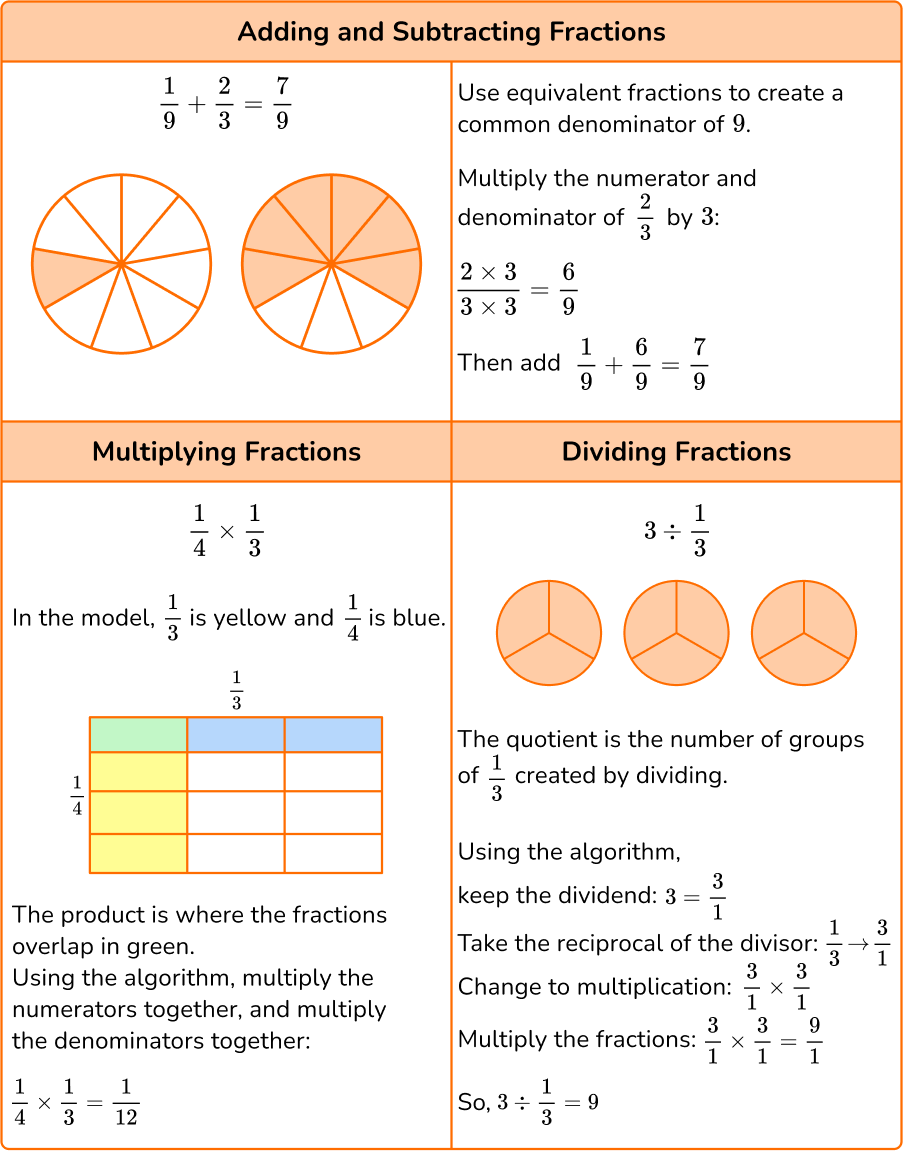
The equation is taking \, \cfrac{1}{8} \, away from \, \cfrac{4}{8} \, .
Since the denominators are the same, the parts are the same size.
You subtract to see how many parts are left: 4-1 = 3.

There are 3 parts and the size is still eighths, so the denominator stays the same.
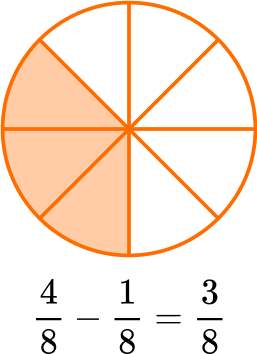
When fractions have unlike denominators, create equivalent fractions with common denominators to solve.
For example,
The parts are NOT the same size, since the denominators are different.
Use equivalent fractions to create a common denominator of 10.
Multiply the numerator and denominator of \, \cfrac{2}{5} \, by 2.
\cfrac{2 \, \times \, 2}{5 \, \times \, 2}=\cfrac{4}{10}
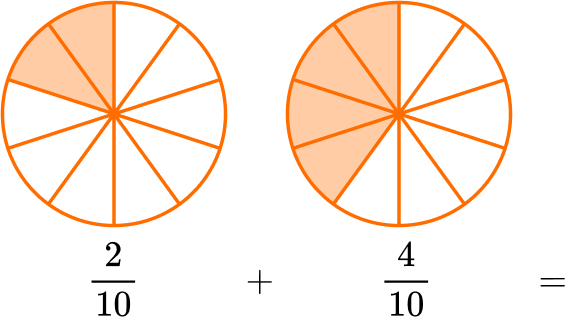
Add to find how many parts there are in all: 2 + 4 = 6.
There are 6 parts and the size is still tenths, so the denominator stays the same.
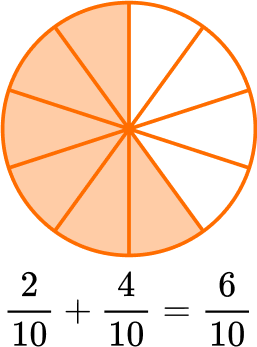
The sum could also be written as the equivalent fraction \, \cfrac{3}{5} \, .
Step-by-step guide: Adding fractions
Step-by-step guide: Subtracting fractions
Step-by-step guide: Adding and subtracting fractions
Multiplying and dividing fractions
Multiplying and dividing fractions means using multiplication and division to calculate with fractions. Fraction multiplication and division can be solved using models or an algorithm.
For example,

Using models:
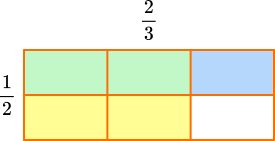
In the model, \, \cfrac{2}{3} \, is yellow and \, \cfrac{1}{2} \, is blue.
The product is where the fractions overlap in green.
The model shows \, \cfrac{2}{3} \, of \, \cfrac{1}{2}, \, so \, \cfrac{1}{2} \times \cfrac{2}{3} = \cfrac{2}{6} \, .
Using the algorithm:
To multiply fractions, you multiply the numerators together, and multiply the denominators together:
\cfrac{1}{2} \, \times \, \cfrac{2}{3}=\cfrac{2}{6} \, .
You can also divide fractions with a model or an algorithm.
For example,

Using models:
Think of this equation as how many \, \cfrac{1}{4} \, fit into \, \cfrac{1}{2} \, .
In the model, \, \cfrac{1}{2} \, is orange and \, \cfrac{1}{4} \, is yellow.
To divide into equal groups, use the equivalent fraction \, \cfrac{2}{4} \, .
The quotient is the final fraction formed when \, \cfrac{2}{4} \, is put into a group of \, \cfrac{1}{4} \, .
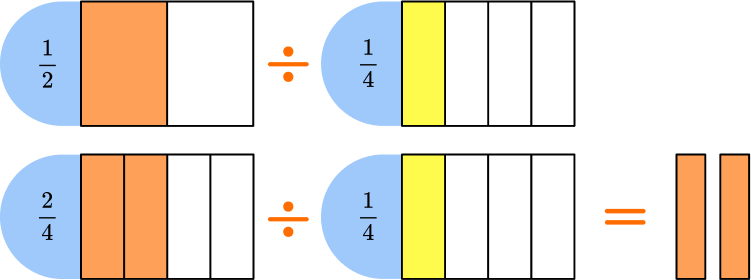
Two groups of \cfrac{1}{4} can be made, so \cfrac{1}{2} \div \cfrac{1}{4}=2.
Using the algorithm:
KEEP the first fraction, FLIP the second fraction, CHANGE to multiplication.
\cfrac{1}{2} \div \cfrac{1}{4}
Keep the dividend (first fraction): \, \cfrac{1}{2}
Take the reciprocal of the divisor (flip the second fraction): \, \cfrac{1}{4} \rightarrow \cfrac{4}{1}
Change to multiplication: \, \cfrac{1}{2} \times \cfrac{4}{1}
Multiply the fractions: \, \cfrac{1}{2} \times \cfrac{4}{1}=\cfrac{4}{2} \, which simplifies to 2.
\cfrac{1}{2} \div \cfrac{1}{4}=2
Since \, \cfrac{1}{2} \, is larger than \, \cfrac{1}{4} \, , the answer makes sense.
A larger number divided by a smaller number, will have a quotient of greater than 1.
Notice that it is not necessary to create a common denominator to multiply and divide fractions when using the algorithm, like it is to add and subtract fractions.
Step-by-step guide: Multiplying fractions
Step-by-step guide: Dividing fractions
Step-by-step guide: Multiplying and dividing fractions
The algorithm for dividing fractions involves using the reciprocal.
When two numbers are multiplied by something other than 1, and have a product of 1, they are reciprocals.
This is also known as the multiplicative inverse.
For example,
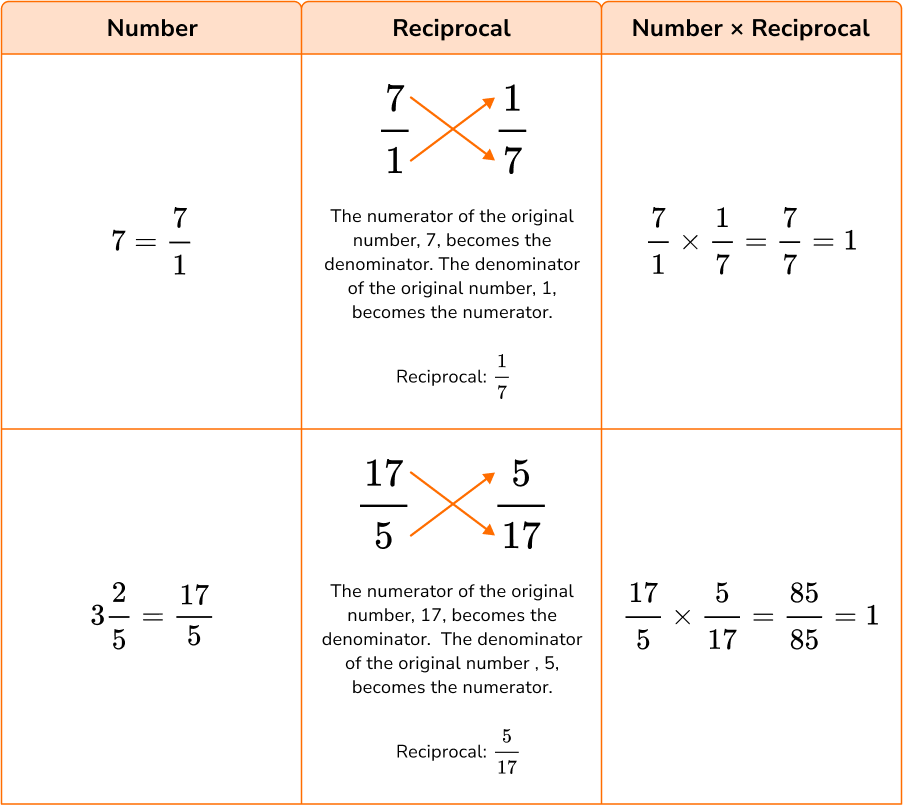
The reciprocal of all numbers can be found by writing the number as a fraction and then flipping it so that the numerator becomes the denominator and the denominator becomes the numerator.
Step-by-step guide: Reciprocal
Step-by-step guide: Multiplicative inverse
What are fractions operations?
Common Core State Standards
How does this relate to 4th grade math, 5th grade math, and 6th grade math?
- Grade 4 – Number and Operations – Fractions (4.NF.B.3a)
Understand addition and subtraction of fractions as joining and separating parts referring to the same whole.
- Grade 4 – Number and Operations – Fractions (4.NF.B.3c)
Add and subtract mixed numbers with like denominators, for example, by replacing each mixed number with an equivalent fraction, and/or by using properties of operations and the relationship between addition and subtraction.
- Grade 4 – Number and Operations – Fractions (4.NF.B.4b)
Understand a multiple of \, \cfrac{a}{b} \, as a multiple of \, \cfrac{1}{b} \, , and use this understanding to multiply a fraction by a whole number.
- Grade 5 – Number and Operations – Fractions (5.NF.A.1)
Add and subtract fractions with unlike denominators (including mixed numbers) by replacing given fractions with equivalent fractions in such a way as to produce an equivalent sum or difference of fractions with like denominators.
For example, \, \cfrac{2}{3} + \cfrac{5}{4} = \cfrac{8}{12} + \cfrac{15}{12} = \cfrac{23}{12} \, . \; (In general, \, \cfrac{a}{b} + \cfrac{c}{d} = \cfrac{(ad \, + \, bc)}{bd} \, . )
- Grade 5 – Number and Operations – Fractions (5.NF.B.4b)
Apply and extend previous understandings of multiplication to multiply a fraction or whole number by a fraction.
- Grade 6 – Number System (6.NS.A.1)
Apply and extend previous understandings of multiplication and division to divide fractions by fractions.
How to use fractions operations
There are a lot of ways to use fractions operations. For more specific step-by-step guides, check out the fraction pages linked in the “What are fractions operations?” section above or read through the examples below.
Fractions operations examples
Example 1: adding fractions with like denominators
Solve \, \cfrac{5}{8}+\cfrac{7}{8} \, .
- Add or subtract the numerators (top numbers).
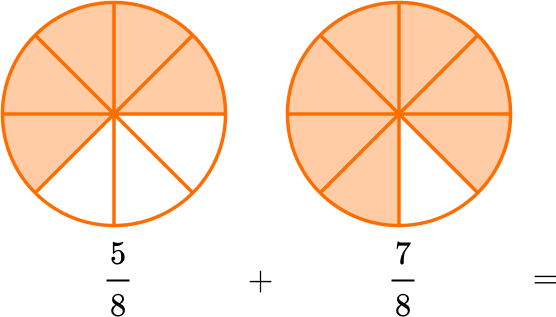
Since the denominators are the same, the parts are the same size. You add to see how many parts there are in total: 5 + 7 = 12.
2Write your answer as a fraction.
There are 12 parts, and the size is still eighths, so the denominator stays the same.
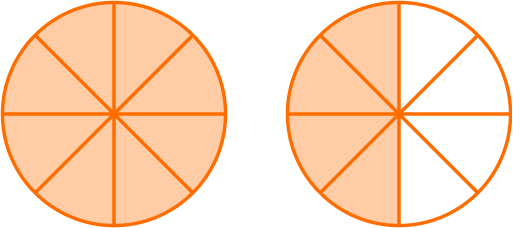
\cfrac{12}{8} \, is an improper fraction and converts to the mixed number 1 \, \cfrac{4}{8} \, .
\cfrac{5}{8}+\cfrac{7}{8}=1 \cfrac{4}{8}
You can also write this answer as the equivalent mixed number \, 1 \cfrac{1}{2} \, .
Example 2: subtracting fractions with unlike denominators
Solve \cfrac{6}{10}-\cfrac{1}{3} \, .
Create common denominators (bottom numbers).
Since \, \cfrac{6}{10} \, and \, \cfrac{1}{3} \, do not have like denominators, the parts are NOT the same size.
Multiply the numerator and denominator by the opposite denominator to create equivalent fractions with common denominators.
\cfrac{6 \, \times \, 3}{10 \, \times \, 3}=\cfrac{18}{30} \quad and \quad \cfrac{1 \, \times \, 10}{3 \, \times \, 10}=\cfrac{10}{30}
Add or subtract the numerators (top numbers).
Now use the equivalent fractions to solve: \, \cfrac{18}{30}-\cfrac{10}{30} \, .
Since the denominators are the same, the parts are the same size. You subtract to see how many parts are left: 18-10 = 8.
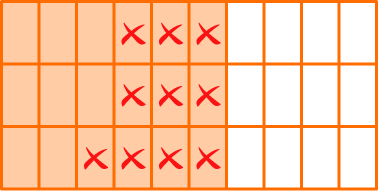
Write your answer as a fraction.
There are 8 parts and the size is still thirtieths, so the denominator stays the same.
\cfrac{18}{30}-\cfrac{10}{30}=\cfrac{8}{30}
You can also write this answer as the equivalent fraction \, \cfrac{4}{15} \, .
Example 3: multiplying a mixed number by a fraction with the algorithm
Solve 1 \, \cfrac{11}{12} \times \cfrac{3}{4} \, .
Convert whole numbers and mixed numbers to improper fractions.
Convert the mixed number to an improper fraction.
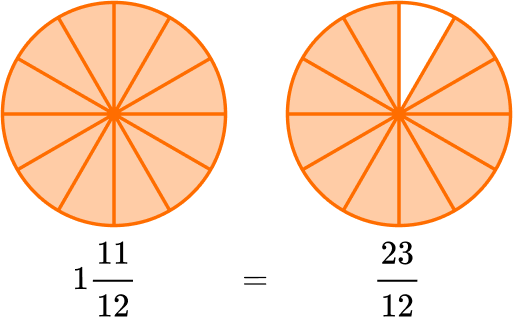
Multiply the numerators together.
\cfrac{23}{12} \times \cfrac{3}{4}=\cfrac{69}{}
Multiply the denominators together.
\cfrac{23}{12} \times \cfrac{3}{4}=\cfrac{69}{48}
If possible, simplify or convert to a mixed number.
The numerator is greater than the denominator, so the improper fraction can be converted to a mixed number.
\cfrac{69}{48}=1 \, \cfrac{21}{48}
The product can be simplified. 21 and 48 have a common factor of 3.
\cfrac{21 \, \div \, 3}{48 \, \div \, 3}=\cfrac{7}{16}
So, \, \cfrac{23}{12} \times \cfrac{3}{4}=\cfrac{69}{48} \, or 1 \, \cfrac{7}{16} \, .
Example 4: dividing a fraction by a fraction
Divide the numbers \, \cfrac{1}{12} \div \cfrac{1}{4} \, .
Take the reciprocal (flip) of the divisor (second fraction).
\cfrac{1}{4} \, → \, \cfrac{4}{1}
Change the division sign to a multiplication sign.
\cfrac{1}{12} \, \times \, \cfrac{4}{1}
Multiply the fractions together.
\cfrac{1}{12} \, \times \, \cfrac{4}{1}=\cfrac{4}{12}
If possible, simplify or convert to a mixed number.
\cfrac{4}{12}=\cfrac{1}{3}
This can also be solved with a model.
You can think of this equation as how many \, \cfrac{1}{4} \, fit into \, \cfrac{1}{12} \, .
In the model, \, \cfrac{1}{12} \, is yellow and \, \cfrac{1}{4} \, is orange.
To divide into equal groups, the fractional pieces need to be the same size.
Use \, \cfrac{1}{12} \, and \, \cfrac{3}{12} \, to solve.
The quotient is the final fraction formed when \, \cfrac{1}{12} \, is put into groups of \, \cfrac{3}{12} \, .
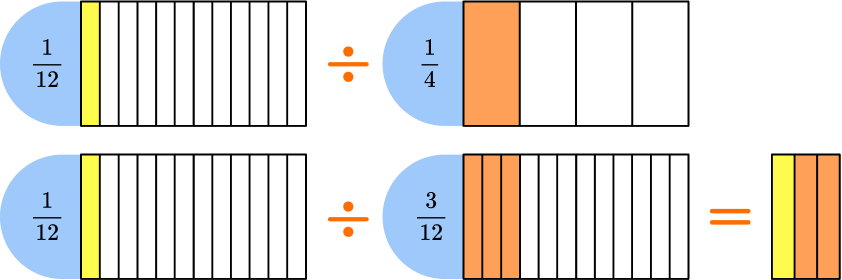
One out of the three parts are filled, so \, \cfrac{1}{12} \div \cfrac{3}{12}=\cfrac{1}{3} \, .
Example 5: adding mixed numbers with unlike denominators
There are 2 \, \cfrac{1}{3} \, pounds of red apples and 4 \, \cfrac{1}{6} \, pounds of green apples.
How many pounds of apples are there in all?
Create an equation to model the problem.
2 \cfrac{1}{3}+4 \cfrac{1}{6}= \, ?
Add or subtract the whole numbers.
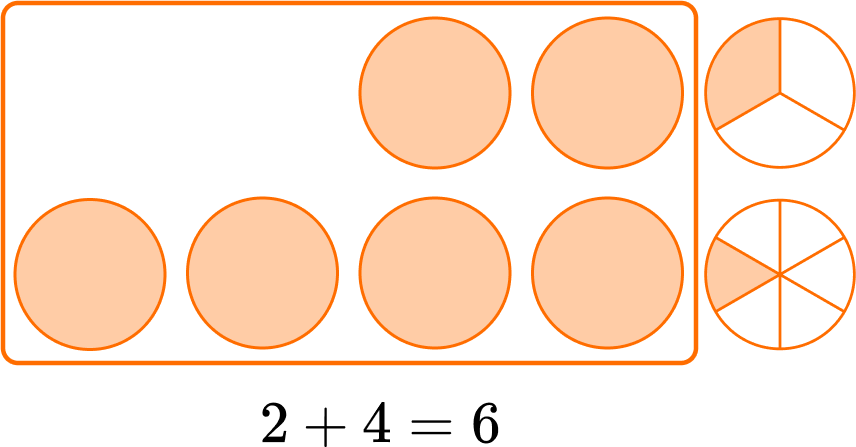
Create common denominators (bottom numbers).

Since \, \cfrac{1}{3} \, and \, \cfrac{1}{6} \, do not have like denominators, the parts are NOT the same size.
Use equivalent fractions to create a common denominator.
A common denominator of 6 can be used.
Multiply the numerator and denominator of \, \cfrac{1}{3} \, by 2 to create an equivalent fraction.
\cfrac{1}{3}=\cfrac{1 \, \times \, 2}{3 \, \times \, 2}=\cfrac{2}{6} \quad and \quad \cfrac{1}{6}
Add or subtract the fractions.
Since the denominators are the same, the parts are the same size. You add to see how many parts there are in total: 2 + 1 = 3.

There are 3 parts, and the size is still sixths, so the denominator stays the same.

Write your answer as a mixed number.
Add the whole number and fraction together.
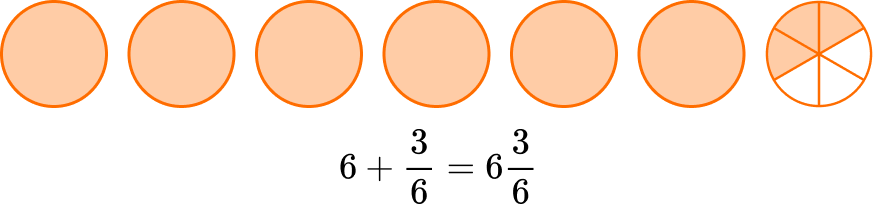
You can also write this answer as the equivalent mixed number 6 \, \cfrac{1}{2} \, .
There are 6 \, \cfrac{1}{2} \, pounds of apples in all.
Example 6: word problem dividing with fractions
Each seed needs \, \cfrac{1}{5} \, cup of soil. How many seeds can be planted with 11 cups of soil?
Create an equation to model the problem.
11 \div \cfrac{1}{5}= \, ?
Change any mixed numbers to an improper fraction.
Change 11 to an improper fraction.
11=\cfrac{11}{1}
Take the reciprocal (flip) of the divisor (second fractions).
\cfrac{1}{5} \, → \, \cfrac{5}{1}
Change the division sign to a multiplication sign.
\cfrac{11}{1} \times \cfrac{5}{1}
Multiply the fractions together.
\cfrac{11}{1} \times \cfrac{5}{1}=\cfrac{55}{1}
If possible, simplify or convert to a mixed number (mixed fraction).
\cfrac{55}{1}=55
55 seeds can be planted with 11 cups of soil.
Teaching tips for fractions operations
- Fraction work in lower grades emphasizes understanding through models, including area models and number lines. To support students in upper grades, always have digital or physical models available for students to use as they work with fractions operations.
- Fraction worksheets can be useful when students are developing understanding around basic operations with fractions. However, when students have successful strategies and can flexibly operate, make the practice more engaging by using math games or real world projects that allow students to use fractions in a variety of situations.
- Highlight patterns within and between the operations as students are learning and encourage them to look for patterns on their own. This will help students make sense of the algorithms used to operate with fractions and minimize conceptual errors.
- Let students find reciprocal numbers on their own by consistently asking questions such as, “What number multiplied by 7 will have a product of 1 ?” Each time this is discussed, write these equations on an anchor chart and students will begin to see a pattern over time.
Although worksheets can serve a purpose and help with skill and test prep practice, having students discover and make sense of mathematical concepts is more meaningful for building long lasting understanding.
Easy mistakes to make
- Adding or subtracting the denominators of fractions
The denominator indicates the size of the parts or whole group. This does not change when a fraction is being added or subtracted, so keep the denominator the same and only add or subtract the numerators.
For example,
- Adding or subtracting unlike denominators
To add or subtract, fractions need to have like denominators. Use equivalent fractions to create a common denominator before adding or subtracting any fractions that have unlike denominators.
For example,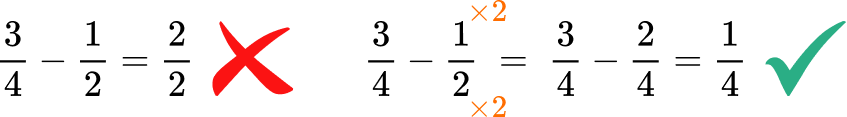
- Finding a common denominator when multiplying or dividing fractions
To use the algorithm, you do not need to find a common denominator to multiply or divide fractions. Using a common denominator won’t automatically give you the wrong answer, but it creates unnecessary calculations and leaves more room for error.
For example,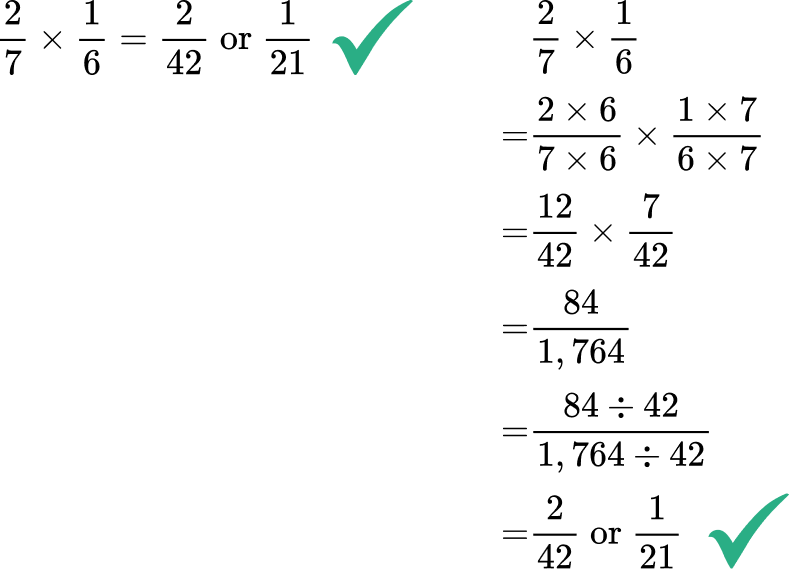
- Using the reciprocal when multiplying
When multiplying fractions, using the reciprocal (flipping the second fraction) changes the value of the equation and will lead to a different answer. The reciprocal is used in the algorithm for division.
For example,
- Forgetting how to find the reciprocal of a whole number
Whole numbers can be written as an improper fraction and then the numerator and denominator of the improper fraction can be flipped to find the reciprocal of the whole number.
For example,
16 can be written as \, \cfrac{16}{1} \, and the reciprocal is \, \cfrac{1}{16} \, .
Practice fractions operations questions
1. Solve \, \cfrac{5}{9}+\cfrac{2}{9} \, .




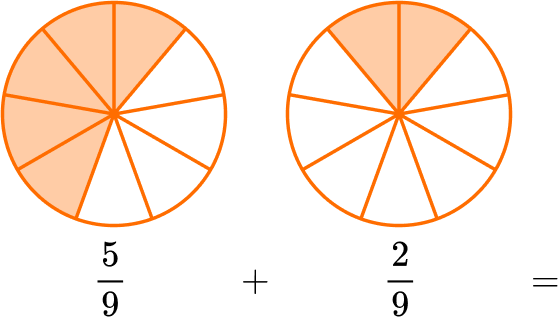
Since the denominators are the same, the parts are the same size. You add to see how many parts there are in total: 5 + 2 = 7.
There are 7 parts and the size is still ninths, so the denominator stays the same.

\cfrac{5}{9}+\cfrac{2}{9}=\cfrac{7}{9}
2. Solve \, 2 \, \cfrac{3}{10}-1 \, \cfrac{4}{5} \, .




The equation is taking \, 1 \cfrac{4}{5} \, away from \, 2 \cfrac{3}{10} \, .
Start with the fractions. Since \, \cfrac{3}{10} \, and \, \cfrac{4}{5} \, do not have like denominators, the parts are NOT the same size.
Use equivalent fractions to create a common denominator. Both denominators are multiples of 10.
\cfrac{3}{10} \quad and \quad \cfrac{4 \, \times \, 2}{5 \, \times \, 2}=\cfrac{8}{10}
Now use the equivalent fraction to solve: 2 \, \cfrac{3}{10}-1 \, \cfrac{8}{10}
Since the denominators are the same, the parts are the same size.
However, there are not enough parts to take 8 away from 3.
You can break one of the wholes into \cfrac{10}{10} \, …
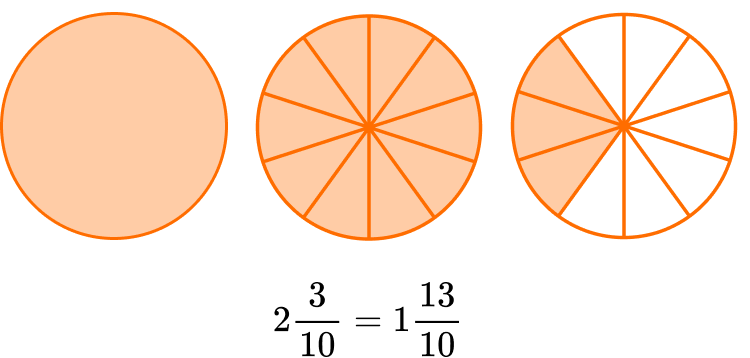
Now you can solve 1 \, \cfrac{13}{10}-1 \, \cfrac{8}{10}.
You subtract to see how many parts are left: 13-8 = 5.

There are 5 parts and the size is still tenths, so the denominator stays the same.
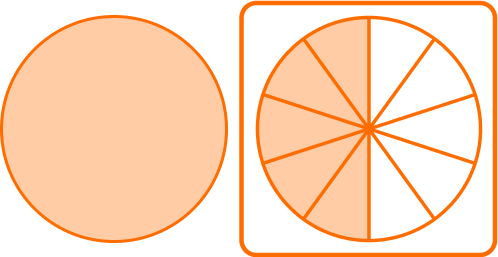
\cfrac{13}{10}-\cfrac{8}{10}=\cfrac{5}{10}
Subtract the whole numbers.
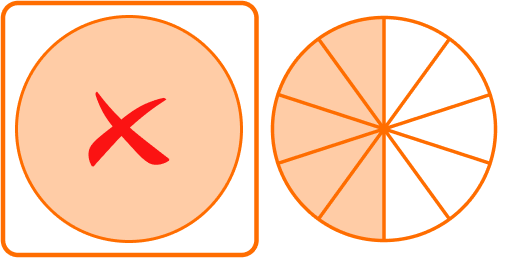
1-1 = 0

1 \, \cfrac{13}{10}-1 \, \cfrac{8}{10}=\cfrac{5}{10}
You can also write this answer as the equivalent fraction \, \cfrac{1}{2} \, .
3. Solve \, \cfrac{1}{4} \times \cfrac{2}{5} \, .




To solve using a model, draw a rectangle. Divide one side into fourths.

Divide the other side into fifths.
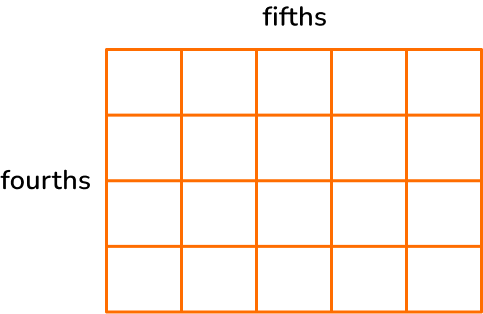
Shade in \, \cfrac{1}{4} \, with yellow and \, \cfrac{2}{5} with blue.
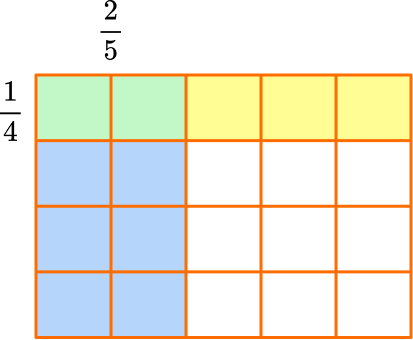
The product is where the fractions overlap in green.
The model shows \, \cfrac{2}{5} \, of \, \cfrac{1}{4} \, , so \, \cfrac{1}{4} \times \cfrac{2}{5}=\cfrac{2}{20} \, , because there are 2 green squares and the whole has 20 squares in total.
The product can be simplified. Both 2 and 20 have a factor of 2, so they can be divided by 2 :
\, \cfrac{2 \, \div \, 2}{20 \, \div \, 2}=\cfrac{1}{10} \, .
So, \, \cfrac{1}{4} \times \cfrac{2}{5}=\cfrac{2}{20} \; or \; \cfrac{1}{10}
4. Solve \, 2 \, \cfrac{1}{6} \div 1 \, \cfrac{2}{3} \, . Write the quotient in lowest terms.




Change the mixed numbers to improper fractions:
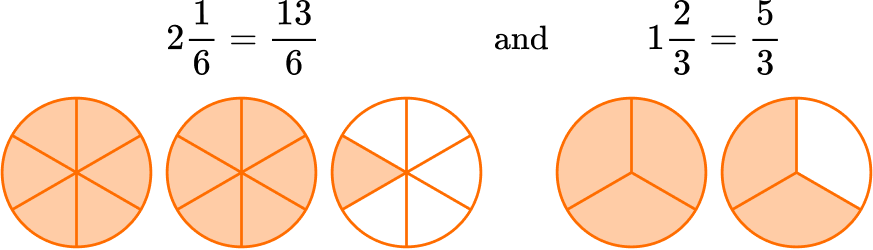
Keep the dividend (first fraction): \, \cfrac{13}{6}
Take the reciprocal of the divisor (flip the second fraction): \, \cfrac{5}{3} → \cfrac{3}{5}
Change to multiplication: \, \cfrac{13}{6} \times \cfrac{3}{5}
Multiply the fractions: \, \cfrac{13}{6} \times \cfrac{3}{5}=\cfrac{39}{30}
Change back into a mixed number: \, \cfrac{39}{30}=1 \, \cfrac{9}{30}
Simplify: \, \cfrac{9 \, \div \, 3}{30 \, \div \, 3}=\cfrac{3}{10} \, , so the answer in lowest terms is \, 1 \, \cfrac{3}{10} \, .
5. Rashad is cutting a 12 \, ft rope into smaller \, \cfrac{2}{3} \, ft pieces. How many smaller pieces of rope will he have?
8 smaller pieces of rope

12 smaller pieces of rope

18 smaller pieces of rope

\cfrac{24}{3} smaller pieces of rope

Use the equation \, 12 \div \cfrac{2}{3}= \, ?
Draw 12 wholes and break them up into thirds.
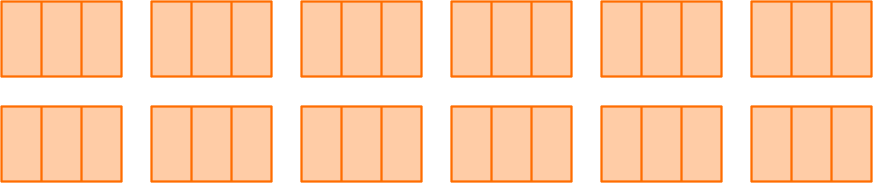
Create groups of \, \cfrac{2}{3} \, .
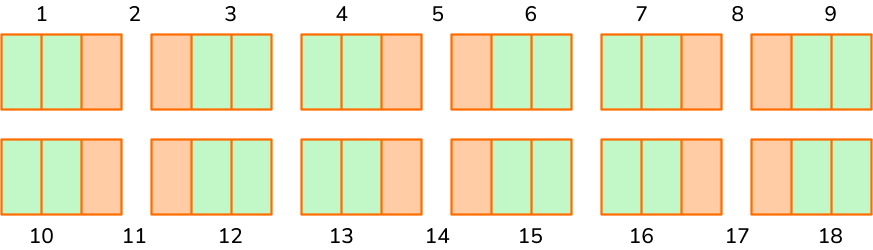
There are 18 groups of \, \cfrac{2}{3} \, .
Rashad will have 18 pieces of smaller rope.
6. A recipe calls for 3 \, \cfrac{1}{4} \, cups of strawberries. If Tyler has 5 \, \cfrac{5}{8} \, cups of strawberries, how many will he have left after he makes 1 recipe?
2 \, \cfrac{3}{8} cups

2 \, \cfrac{4}{4} cups

8 \, \cfrac{7}{8} cups

8 \, \cfrac{6}{12} cups

Use the equation 5 \cfrac{5}{8}-3 \cfrac{1}{4}= \, ?
Start with the fraction.
Since \, \cfrac{5}{8} \, and \, \cfrac{1}{4} \, do not have like denominators, the parts are NOT the same size.
Use equivalent fractions to create a common denominator.
A common denominator of 8 can be used.
Multiply the numerator and denominator of \, \cfrac{1}{4} \, by 2 to create an equivalent fraction.
\cfrac{5}{8} \quad and \quad \cfrac{1}{4}=\cfrac{1 \, \times \, 2}{4 \, \times \, 2}=\cfrac{2}{8}
Since the denominators are the same, the parts are the same size.
You subtract to see how many parts there are in total: 5-2 = 3.

There are 2 parts and the size is still eighths, so the denominator stays the same.
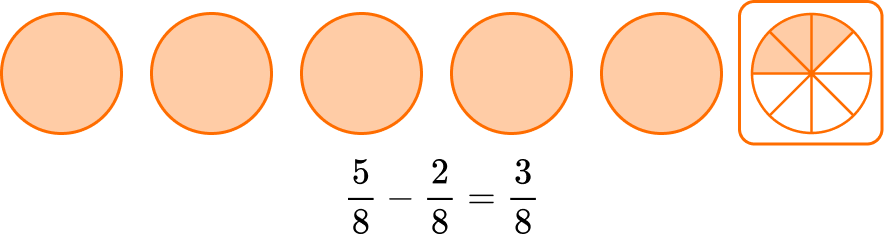
Subtract the whole numbers.

5-3 = 2

There will be \, 2 \cfrac{3}{8} \, cups of strawberries left.
Fractions operations FAQs
No, although using these operations will create different denominators and numerators, as long as they are multiplied or divided by the same thing, the value of the fraction will remain the same.
No, unless the question specifies the lowest terms, it is valid to answer without using the least common denominator (LCD). However, as students progress in their understanding of fractions, it is a good idea to encourage them to practice this skill. Also be mindful of standard expectations, as they may vary from state to state.
Yes, just like any other type of number, to solve multistep problems correctly, the order of operations must be followed.
The multiplicative inverse of a number is the reciprocal. For any integer, that is the number written as the numerator over a denominator of 1. For any rational number, that is switching the numerator and denominator.
The next lessons are
Still stuck?
At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.
Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.

Find out how we can help your students achieve success with our math tutoring programs.
[FREE] Common Core Practice Tests (Grades 3 to 6)
Prepare for math tests in your state with these Grade 3 to Grade 6 practice assessments for Common Core and state equivalents.
40 multiple choice questions and detailed answers to support test prep, created by US math experts covering a range of topics!