[FREE] Fun Math Games & Activities Packs
Always on the lookout for fun math games and activities in the classroom? Try our ready-to-go printable packs for students to complete independently or with a partner!
In order to access this I need to be confident with:
Equivalent fractions Comparing decimalsComparing percentages
Percents Fractions DecimalsConverting fractions, decimals and percents
Here you will learn about comparing fractions, decimals, and percentages, including how to define a fraction, a decimal, and a percentage, convert between them, and compare and order them.
Students first learn about comparing fractions and decimals in the fifth grade and expand this knowledge to percents in the sixth and seventh grades when working with ratio and proportional relationships and the number system.
What are fractions, decimals, and percents?
Fractions, decimals, and percentages are different ways of expressing the same value.
- Fractions
Fractions equal parts of a whole.
The denominator of a fraction (number below the line) shows how many equal parts the whole has been divided into. The numerator of a fraction (number above the line) shows how many of the equal parts we have.
3 parts shaded out of 5 equal parts.
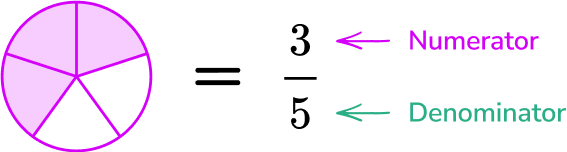
Read as three-fifths
See also: Fractions
- Decimals
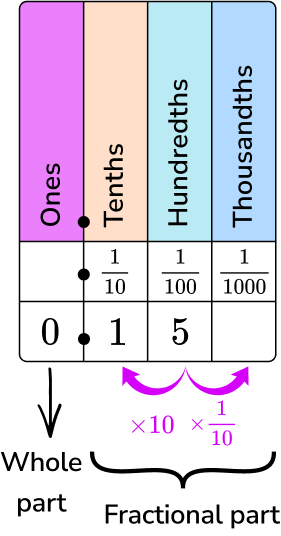
Decimals are numbers that have a whole part and a fractional part that are separated by a decimal point. Our decimal system splits whole numbers into tenths, hundredths, thousandths, and so on.
0.15 is represented on the place value chart.
Read as fifteen-hundredths.
See also: Decimals
- Percentages
Percentages are numbers which are expressed as a fraction of 100. Percent means “number of parts per hundred” and the symbol used for percent is, \% (percent sign).
42 shaded parts out of 100 equal parts is \, \cfrac{42}{100} \, which is 42\% .

See also: Percents
Let’s look at how you can express twenty-hundredths, \, \cfrac{20}{100} \, , as a fraction, decimal and percent.
| FRACTION | DECIMAL | PERCENT |
|---|---|---|
As a fraction: \cfrac{20}{100}=\cfrac{20\div 20}{100\div 20}= \cfrac{1}{5} 20 shaded pieces out of 100 equal pieces.  1 shaded piece out of 5 equal pieces.  | As a decimal:
\cfrac{20}{100}=0.20 20 shaded pieces where each piece represents 0.01.  | As a percent:
\cfrac{20}{100}=20 \% 20 shaded pieces out of 100 pieces.  |
What is converting fractions, decimals, and percents?
In order to compare fractions, decimals and percentages, you will need to know how to convert them to the same form.
Converting Fractions, Decimals, and Percents \hspace{1.2cm}
to Fractions with a Denominator of \textbf{100} \hspace{1.2cm}
| Fractions
(Use equivalent fractions) | Decimals
(Numbers to right of decimal point are the numerator of the fraction) | Percents
(Percents are fractions of \textbf{100} ) |
|---|---|---|
\cfrac{1}{2}=\cfrac{1\times 50}{2 \times 50}=\cfrac{50}{100} | 0.50=\cfrac{50}{100} | 50 \%=\cfrac{50}{100} |
\cfrac{3}{4}=\cfrac{3\times 25}{4\times 25}=\cfrac{75}{100} | 0.75=\cfrac{75}{100} | 75\%=\cfrac{75}{100} |
\cfrac{3}{10}=\cfrac{3\times 10}{10 \times 10}=\cfrac{30}{100} | 0.30=\cfrac{30}{100} | 30\%=\cfrac{30}{100} |
Step-by-step guide: Decimal to a fraction
Step-by-step guide: Percent to a fraction
Converting Fractions & Decimals \hspace{1.2cm}
to Percents \hspace{1.2cm}
| Fractions
(Use equivalent fractions) | Decimals
(Multiply decimal by \textbf{100} ) |
|---|---|
\cfrac{1}{2}=\cfrac{1 \times 50}{2\times 100}=\cfrac{50}{100}=50\% | 0.50\times 100 = 50
50\% |
\cfrac{3}{4}=\cfrac{3 \times 25}{4\times25}=\cfrac{75}{100}=75\% | 0.75\times 100 = 75
75\% |
\cfrac{3}{10}=\cfrac{3 \times 10}{10\times10}=\cfrac{30}{100}=30\% | 0.30\times 100 = 30
30\% |
Step-by-step guide: Decimal to a percent
Step-by-step guide: Fraction to a percent
See also: Powers of 10
Converting Fractions and Percents \hspace{1.2cm}
to Decimals \hspace{1.2cm}
| Fractions
(Use long division) | Decimals
(Change to a fraction and then decimal in the hundredths place) |
|---|---|
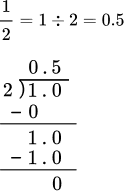 | 50\%=\cfrac{50}{100}=0.50=0.5
Notice how 50 becomes 0.50 which is the same as dividing 50 by 100 |
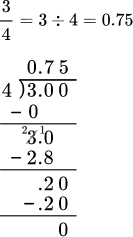 | 75\%=\cfrac{75}{100}=0.75
Notice how 75 becomes 0.75 which is the same as dividing 75 by 100 |
 | 33\%=\cfrac{33}{100} =0.33
Notice how 33 becomes 0.33 which is the same as dividing 33 by 100 |
Step-by-step guide: Fraction to a decimal
Step-by-step guide: Percent to a decimal
![[FREE] Converting Fractions, Decimals and Percents Worksheet (Grade 4 to 6)](https://thirdspacelearning.com/wp-content/uploads/2023/07/Converting-fractions-decimals-and-percents-check-for-understanding-quiz-listing-image-.png)
[FREE] Converting Fractions, Decimals and Percents Worksheet (Grade 4 to 6)
![[FREE] Converting Fractions, Decimals and Percents Worksheet (Grade 4 to 6)](https://thirdspacelearning.com/wp-content/uploads/2023/07/Converting-fractions-decimals-and-percents-check-for-understanding-quiz-listing-image-.png)
Use this quiz to assess your grade 4 to 6 students’ understanding of converting fractions, decimals, and percents. 10+ questions with answers to identify areas of strength and support!
DOWNLOAD FREE![[FREE] Converting Fractions, Decimals and Percents Worksheet (Grade 4 to 6)](https://thirdspacelearning.com/wp-content/uploads/2023/07/Converting-fractions-decimals-and-percents-check-for-understanding-quiz-listing-image-.png)
[FREE] Converting Fractions, Decimals and Percents Worksheet (Grade 4 to 6)
![[FREE] Converting Fractions, Decimals and Percents Worksheet (Grade 4 to 6)](https://thirdspacelearning.com/wp-content/uploads/2023/07/Converting-fractions-decimals-and-percents-check-for-understanding-quiz-listing-image-.png)
Use this quiz to assess your grade 4 to 6 students’ understanding of converting fractions, decimals, and percents. 10+ questions with answers to identify areas of strength and support!
DOWNLOAD FREEComparing fractions, decimals, and percents
Now that you know how to convert fractions, decimals, and percents to the same form, let’s compare them.
For example, list the following numbers in order from least to greatest.
\cfrac{1}{4} \hspace{0.5cm} 0.19 \hspace{0.5cm} 0.3 \hspace{0.5cm} 26 \% \hspace{0.5cm} \cfrac{1}{5}
Before comparing the numbers, convert them all to fractions with a denominator of 100.
\cfrac{1}{4}=\cfrac{1 \, \times \, 25}{4 \, \times \, 25}=\cfrac{25}{100}
0.19=\cfrac{19}{100}
0.3=\cfrac{3}{10}=\cfrac{3 \, \times \, 10}{10 \, \times \, 10}=\cfrac{30}{100}
26 \%=\cfrac{26}{100}
\cfrac{1}{5}=\cfrac{1 \, \times \, 20}{5 \, \times \, 20}=\cfrac{20}{100}
The numbers in order from least to greatest:
0.19=\cfrac{19}{100} \, , \; \cfrac{1}{5}=\cfrac{20}{100} \, , \; \cfrac{1}{4}=\cfrac{25}{100} \, , \; 26 \%=\cfrac{26}{100} \, , \; 0.3=\cfrac{30}{100}
0.19, \; \cfrac{1}{5} \, , \; \cfrac{1}{4} \, , \; 26 \%, \; 0.3
Another way you could have done the comparison is to convert all the numbers to percents.
\cfrac{1}{4}=\cfrac{25}{100}=25 \%
0.19 \, → multiply by 100 to change a decimal to a percent.
0.19 \times 100=19. This is the same as moving the decimal point 2 decimal places to the right.
0.19=19 \%
0.3 \, → multiplied by 100 changes a decimal to a percent.
0.3 \times 100=30. This is the same as moving the decimal point 2 decimal places to the right.
0.3=30 \%
\cfrac{1}{5}=\cfrac{20}{100}=20 \%
The numbers from least to greatest is:
0.19=19 \%, \; \cfrac{1}{5}=20 \% \, , \; \cfrac{1}{4}=25 \%, \; 26 \%, \; 0.3=30 \%
0.19, \; \cfrac{1}{5} \, , \; \cfrac{1}{4} \, , \; 26 \%, \; 0.3
What are fractions, decimals and percents?

Common Core State Standards
How does this relate to 5th grade math, 6th grade math and 7th grade math?
- Grade 5 – Number and Operations – Base Ten (5.NBT.A.3.a)
Read and write decimals to thousandths using base-ten numerals, number names, and expanded form, for example,
347.392 = 3 \times 100 + 4 \times 10 + 7 \times 1 + 3 \times \bigl(\cfrac{1}{10}\bigr) + 9 \times \bigl(\cfrac{1}{100}\bigr) + 2 \times \bigl(\cfrac{1}{1000}\bigr).
- Grade 6 – Ratios and Proportional Relationships (6.RP.A.3.c)
Find a percent of a quantity as a rate per 100 (for example, 30\% of a quantity means \; \cfrac{30}{100} \; times the quantity); solve problems involving finding the whole, given a part and the percent.
- Grade 7 – The Number System (7.NS.2d)
Convert a rational number to a decimal using long division; know that the decimal form of a rational number terminates in 0s or eventually repeats.
How do you convert fractions, decimals, and percents?
In order to compare fractions, decimals, and percentages, convert them to the same form.
- Choose a form (fraction, decimal, percentage).
- Convert the numbers to the form you chose.
- Write the numbers in the new form. If you’re comparing the numbers, go to Step 4.
- Write the numbers in the correct order.
Converting fractions, decimals, and percents examples
Example 1: convert fraction, decimal, and percentage to the same form
Convert the numbers below to fractions with a denominator of 100.
\cfrac{3}{4} \, , \; 75 \%, \; 0.75
- Choose a form (fraction, decimal, percentage).
Convert the numbers to fractions.
2Convert the numbers to the form you chose.
Since you are converting the numbers to fractions, use equivalent fractions to convert the denominator of the fraction to 100.
\cfrac{3}{4}= \cfrac{3 \, \times \, 25}{4 \, \times \, 25}= \cfrac{75}{100}
\cfrac{3}{4}= \cfrac{75}{100}
Write the decimal as a fraction.
0.75 is seventy-five hundredths, which is \, \cfrac{75}{100} .
Write the percent as a fraction.
75 \% is \, \cfrac{75}{100} \, .
3Write the numbers in the new form. If you’re comparing the numbers, go to Step 4.
\cfrac{3}{4}= \cfrac{75}{100}
0.75= \cfrac{75}{100}
75 \% =\cfrac{75}{100}
You are not comparing the numbers, so you do not have to go to Step 4.
Example 2: convert fraction, decimal and percentage to a decimal
Convert the numbers below to decimals.
\cfrac{2}{5} \, , \; 40 \%
Choose a form (fraction, decimal, percentage).
Convert the numbers to decimal numbers.
Convert the numbers to the form you chose.
Rewrite the fraction as a division problem, then use long division to divide the numerator by the denominator.
2 \div 5
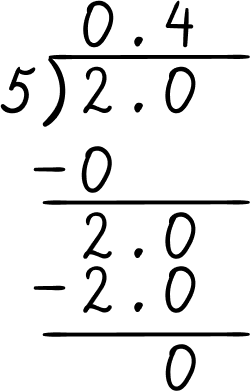
2 \div 5=0.4
Divide the percent number by 100.
40 \% =\cfrac{40}{100} = {40}\div 100
Recall from dividing by powers of 10, you can simply move the decimal point two places to the left when dividing by 100.
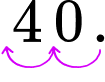
Write the numbers in the new form. If you’re comparing the numbers, go to Step 4.
\cfrac{2}{5}=0.40=0.4
40 \%=\cfrac{40}{100} = 0.40 = 0.4
You are not comparing the numbers, so do not need to go to Step 4.
Example 3: convert fraction, decimal, and percentage to decimals
Convert the numbers below to decimals.
\cfrac{2}{9} \, , \; 67 \%
Choose a form (fraction, decimal, percentage).
Convert the numbers to decimal numbers.
Convert the numbers to the form you chose.
Divide the numerator by the denominator using long division \, \cfrac{2}{9} = 2\div 9
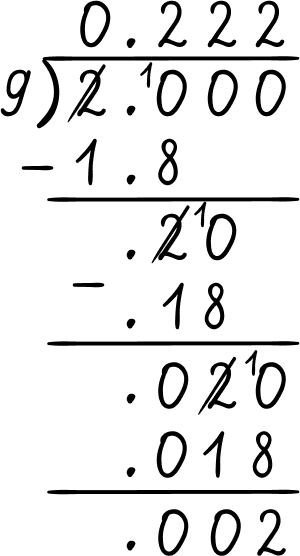
2 \div 9=0 . \overline{2}
Make the percent a decimal by dividing the percent by 100 which is the same as moving the decimal point two places to the left.
67\%=\cfrac{67}{100} = 67\div 100
Using the rules of dividing by powers of ten 67 \div 100=0.67
Write the numbers in the new form. If you’re comparing the numbers, go to Step 4.
\cfrac{2}{9} = 0.\overline{2}
0.\overline{2} rounded to the nearest hundredth is 0.22
67\% = 0.67
You are not comparing the numbers, so you do not have to go to Step 4.
Example 4: compare fractions, decimals, and percentage by converting them to fractions
Write the numbers in order from least to greatest.
\cfrac{1}{2} \, , \; 0.24,33 \%, \; \cfrac{7}{20}
Choose a form (fraction, decimal, percentage).
Change all the numbers to fractions with a denominator of 100.
Convert the numbers to the form you chose.
Change \, \cfrac{1}{2} \, and \, \cfrac{7}{20} \, so they have a denominator of 100.
\cfrac{1}{2}=\cfrac{1 \, \times \, 50}{2 \, \times \, 50}=\cfrac{50}{100}
\cfrac{7}{20}=\cfrac{7 \, \times \, 5}{20 \, \times \, 5}=\cfrac{35}{100}
0.24 is twenty-four hundredths so can be written as \, \cfrac{24}{100} .
33\% can be written as the fraction \, \cfrac{33}{100} .
Write the numbers in the new form. If you’re comparing the numbers, go to Step 4.
The numbers as fractions are:
\cfrac{1}{2}=\cfrac{50}{100}
\cfrac{7}{20}=\cfrac{35}{100}
0.24=\cfrac{24}{100}
33\%=\cfrac{33}{100}
Write the numbers in the correct order.
The numbers in order from least to greatest are:
\cfrac{24}{100} \, , \; \cfrac{33}{100} \, , \; \cfrac{35}{100} \, , \; \cfrac{50}{100} \, which is 0.24, \; 33\%, \; \cfrac{7}{20} \, , \; \cfrac{1}{2}
Example 5: compare fractions, decimals, and percentage by changing them all to percentages
Write the numbers in order from greatest to least.
45\% , \; 0.32, \; \cfrac{1}{4} \, , \; \cfrac{2}{5} \, , \; 0.18
Choose a form (fraction, decimal, percentage).
Change all the numbers to percents.
Convert the numbers to the form you chose.
Rewrite the fractions with a denominator of 100.
\cfrac{1}{4} \; \rightarrow \; \cfrac{1}{4}=\cfrac{1 \, \times \, 25}{4 \, \times \, 25}=\cfrac{25}{100}
\cfrac{2}{5} \; \rightarrow \; \cfrac{2}{5}=\cfrac{2 \, \times \, 20}{5 \, \times \, 20}=\cfrac{40}{100}
\cfrac{25}{100}=25\%
\cfrac{40}{100}= 40\%
Multiply the decimals by 100 or move the decimal point two places to the right.
0.32 \; \rightarrow \; 0.32 \times 100=32 \; \rightarrow \; 32 \%
0.18 \; \rightarrow \; 0.18 \times 100=18 \; \rightarrow \; 18 \%
Write the numbers in the new form. If you’re comparing the numbers, go to Step 4.
45\%
\cfrac{40}{100}= 40\%
0.32= 32\%
\cfrac{25}{100}=25\%
0.18 = 18\%
Write the numbers in the correct order.
The numbers in order from greatest to least are:
45 \%, \, 40 \%, \, 32 \%, \, 25 \%, \, 18 \% \; \rightarrow \; 45 \%, \, \cfrac{2}{5} \, , \, 0.32, \, \cfrac{1}{4} \, , \, 0.18
Example 6: compare fractions, decimals, and percentage by changing them all to decimals
Write the numbers in order from least to greatest.
78 \%, \; 0.9, \; \cfrac{2}{3} \, , \; 61 \%
Choose a form (fraction, decimal, percentage).
Change all the numbers to decimals.
Convert the numbers to the form you chose.
Divide the numerator by the denominator using long division, \, \cfrac{2}{3} \, is 2 \div 3
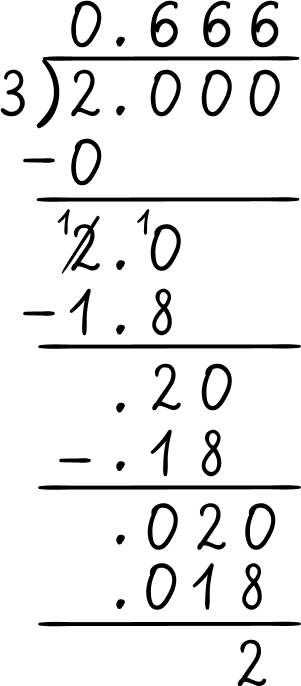
2 \div 3=0 . \overline{6} which is a repeating decimal.
0 . \overline{6}=0.66666\ldots
0.66666\ldots Rounded to the nearest hundredth is 0.67
To change the percents to decimals, divide the percents by 100 or move the decimal point two places to the left.
78 \%=\cfrac{78}{100}=78 \div 100
Using the rules of dividing by powers of ten, 78 \div 100 = 0.78
61 \%=\cfrac{61}{100}=61 \div 100
Using the rules of dividing by powers of ten, 61 \div 100 = 0.61
Write the numbers in the new form. If you’re comparing the numbers, go to Step 4.
\begin{aligned} & 61 \%=0.61, \\\\ & \cfrac{2}{3}=0.67, \\\\ & 78 \%=0.78 \\\\ & 0.9 \end{aligned}
Write the numbers in the correct order.
The numbers in order from least to greatest are:
0.61, \; 0.67, \; 0.78, \; 0.9 \; \rightarrow \; 61 \%, \; \cfrac{2}{3}, \; 78 \%, \; 0.9
Teaching tips for comparing fractions, decimals, and percents
- Use visual models so students can see the connections between fractions, decimals, and percentages.
- When first comparing fractions, decimals, and percentages, start by first converting the numbers into either fractions with a denominator of 100 or percentages. It is usually the easiest way for students to compare the numbers.
- Long division is useful when converting fractions and percentages to decimals, be sure to review the process with students.
- Fraction worksheets, decimal worksheets, and percent worksheets have their place, but using strategies to develop conceptual understanding is more meaningful to your learners.
Easy mistakes to make
- Not remembering the definition of a percent
Not remembering the definition of a percent which is a fraction of 100. All percents can be written as a fraction over 100, which is useful when comparing fractions, decimals, and percents.
- Not remembering to make the denominator \bf{100} when comparing fractions, decimals, and percents
For example, when converting 0.7 to a fraction, leave it as is \, \cfrac{7}{10} instead of changing it to \, \cfrac{70}{100}.
- Writing the answer in the wrong order
For example, writing the numbers in ascending order means writing them from least to greatest. Writing the numbers in descending order means writing them from greatest to least.
- Original values
Not giving the final answer in the value’s original form.
For example, after converting the numbers to the same form to compare them, you forget to write the final answer using the original numbers and not the converted numbers.
Practice comparing fractions, decimals, and percents questions
1. Which of the following is not equivalent to 50\% ?




\cfrac{5}{100} = 5\%
The definition of a percent is a fraction of 100.
So, any fraction that has a denominator of 100 can easily be made into a percent by writing the numerator as the percent.
2. Which of the following is equivalent to \cfrac{1}{4} \, ?




\cfrac{1}{4}=\cfrac{1 \, \times \, 25}{4 \, \times \, 25}=\cfrac{25}{100}
\cfrac{25}{100} \, is 25\% because a fraction with a denominator of 100 can be written as a percent, where the numerator represents the percent.
3. Which of the following represents an equivalent relationship?




2\% as a fraction is \, \cfrac{2}{100} .
0.02 (two-hundredths) as a fraction is \, \cfrac{2}{100} .
So, 2\% as a fraction is \, \cfrac{2}{100} \, and 0.02 as a fraction is \, \cfrac{2}{100} \, , which means 2\% =\cfrac{2}{100}= 0.02
4. Which value below is greater than \, \cfrac{4}{5} \, ?




\cfrac{4}{5} \; → \; \cfrac{4}{5}= 4\div 5 = 0.8
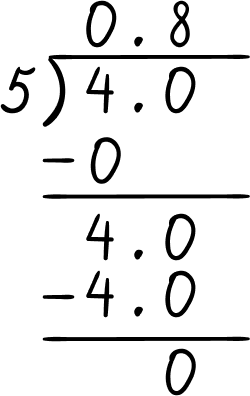
0.8 as a percent is 80 \% because you can multiply 0.8 \times 100 = 80
0.5 is not correct because 0.5 < 0.8 \; \bigl( \cfrac{4}{5} \, \bigr)
80 \% is not correct, because 80 \%= 80 \% \; \bigl( \cfrac{4}{5} \, \bigr)
\cfrac{40}{50} \, is not correct, because \cfrac{40}{50}=\cfrac{4}{5}
84\% > 80\% \; \bigl( \cfrac{4}{5} \, \bigr)
5. Put the numbers below in ascending order (least to greatest).
0.3, \; 32 \%, \; \cfrac{31}{100}




Write the numbers in the same form (make them percents).
Multiply 0.3 by 100 to make it a percent number.
0.3 \times 100 = 30 = 30\%
\cfrac{31}{100} \, is 31 \% because any fraction over 100 can be written as a percent where the numerator represents the percent number.
In order from least to greatest:
30\%, \; 31\%, \; 32\% \; → \; 0.3, \; \cfrac{31}{100} \, , \; 32\%
6. Put the numbers below in descending order (greatest to least).
\cfrac{7}{9} \, , \; 70 \%, \; 0.79




Change the numbers to the same form (make them decimals).
\cfrac{7}{9}= 7\div 9 = 0.\overline{7}
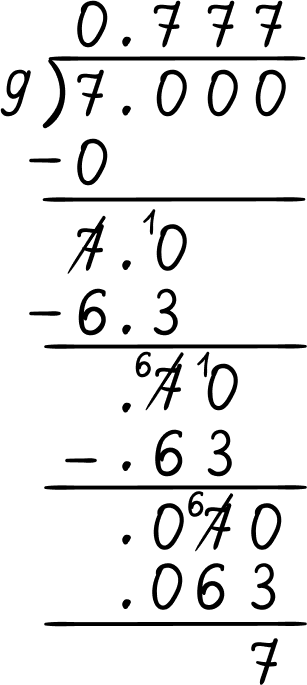
0.\overline{7} = 0.77777… rounded to the nearest hundredth is 0.78 .
70 \% is \, \cfrac{70}{100}= 70\div 100 = 0.70
The numbers in descending order are:
0.79, \; 0.78, \; 0.70 \; → \; 0.79, \; \cfrac{7}{9} \, , 0.70
Comparing fractions, decimals, and percents FAQs
Yes, when you get into 8th grade math and high school math, there is an algebraic process you can use to directly convert a repeating decimal into a fraction.
Step-by-step guide: Repeating decimal to fraction
Yes, when changing a decimal number to a percent you can move the decimal point two places to the right. This is because from the patterns you learned from multiplying by powers of 10, multiplying by 100 is the same as moving the decimal point two places to the right.
0.27 \times 100=27
You can move the decimal point two places to the right.![]()
Yes, using the rules for dividing by powers of ten you can always move the decimal point two decimal places to the left when dividing by 100.
65 \%=\cfrac{65}{100}=65\div 100 = 0.65 ![]()
Yes, you can convert improper fractions to percents the same way you convert proper fractions to percents.
For example, \cfrac{5}{4} can be converted to a percent by making the denominator 100.
\cfrac{5 \, \times \, 25}{4 \, \times \, 25}=\cfrac{125}{100}= 125\%. The percent will be greater than 100.
The next lessons are
- Percent
- Compound measures
- Arithmetic
- Properties of equality
Still stuck?
At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.
Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.

Find out how we can help your students achieve success with our math tutoring programs.
[FREE] Common Core Practice Tests (Grades 3 to 6)
Prepare for math tests in your state with these Grade 3 to Grade 6 practice assessments for Common Core and state equivalents.
40 multiple choice questions and detailed answers to support test prep, created by US math experts covering a range of topics!