[FREE] Fun Math Games & Activities Packs
Always on the lookout for fun math games and activities in the classroom? Try our ready-to-go printable packs for students to complete independently or with a partner!
In order to access this I need to be confident with:
Adding and subtracting fractions Adding and subtracting decimals Multiplying and dividing decimals Multiplying and dividing fractions Rational numbers Multiplying and dividing integersArithmetic
Here you will learn about arithmetic, including key terminology and mathematical symbols, using the four operations with positive and negative integers, and inverse operations.
Students will first learn about arithmetic as part of number and operations in 4th and 5th grade and continue to build on this knowledge in the number system in 6th and 7th grade.
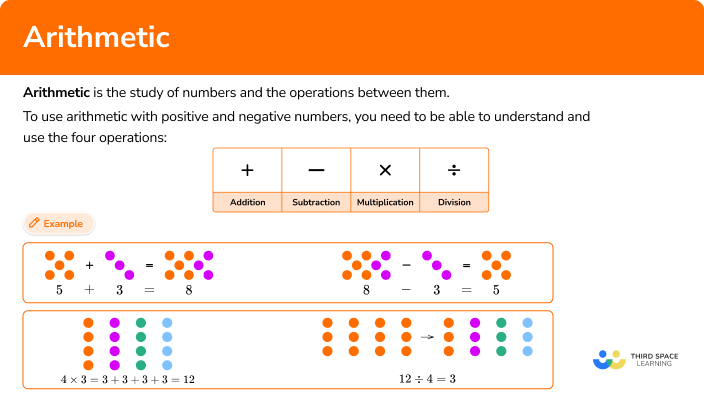
What is arithmetic?
Arithmetic is the study of numbers and the operations between them. It is an elementary branch of mathematics.
The definition of arithmetic comes from the Greek word “arithmos”, meaning number, or the art of counting.
To solve problems using basic arithmetic, you need to understand and use the four operations.
The four operations you will be using are: addition, subtraction, multiplication, and division.
Arithmetic with four operations
Below is a table showing the four operations of arithmetic with their associated symbols.
| Addition | Subtraction | Multiplication | Division |
Each operation has a different function that you should be confident with using.
Addition
Addition is the operation of combining two or more numbers together.
The two numbers can be represented by a and b, and c will represent the sum of a and b.
This would be written as a+b=c and pronounced a plus b is equal to c.
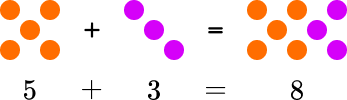
Addition is commutative, which means that the order in which addition is carried out does not matter.
For example,
3+4=4+3=7Addition can be done with positive and negative integers, fractions, and decimals.
Addition represents a movement up the number line. Here are some examples:
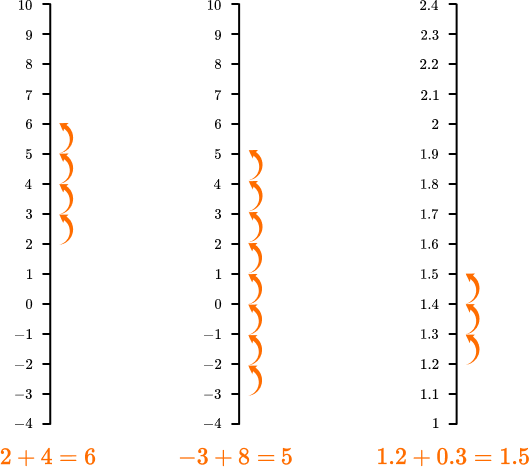
In order to solve addition problems with larger numbers, you can use the standard algorithm.
For example, 347+21 :
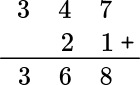
It is important to consider the place value of each digit and line up the corresponding digits in each number.
![[FREE] Arithmetic Worksheet (Grade 4 to 6)](https://thirdspacelearning.com/wp-content/uploads/2023/07/Arithmetic-check-for-understanding-quiz-listing-image-.png)
[FREE] Arithmetic Worksheet (Grade 4 to 6)
![[FREE] Arithmetic Worksheet (Grade 4 to 6)](https://thirdspacelearning.com/wp-content/uploads/2023/07/Arithmetic-check-for-understanding-quiz-listing-image-.png)
Use this quiz to check your grade 4 to 6 students’ understanding of arithmetic. 10+ questions with answers to identify areas of strength and support!
DOWNLOAD FREE![[FREE] Arithmetic Worksheet (Grade 4 to 6)](https://thirdspacelearning.com/wp-content/uploads/2023/07/Arithmetic-check-for-understanding-quiz-listing-image-.png)
[FREE] Arithmetic Worksheet (Grade 4 to 6)
![[FREE] Arithmetic Worksheet (Grade 4 to 6)](https://thirdspacelearning.com/wp-content/uploads/2023/07/Arithmetic-check-for-understanding-quiz-listing-image-.png)
Use this quiz to check your grade 4 to 6 students’ understanding of arithmetic. 10+ questions with answers to identify areas of strength and support!
DOWNLOAD FREESubtraction
Subtraction is the operation of finding the difference between two numbers.
The number remaining when the number b is subtracted from the number c would equal a, or the answer to a subtraction problem.
This would be written as c-b=a and pronounced c take away b is equal to a.
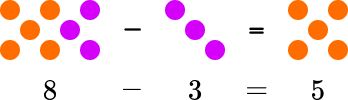
Subtraction is not commutative. If the order of the numbers within the calculation changes, the result will change.
For example,
7-4
Subtraction can also be done with positive and negative integers, fractions, and decimals. Subtraction represents a movement down the number line. Here are some examples:
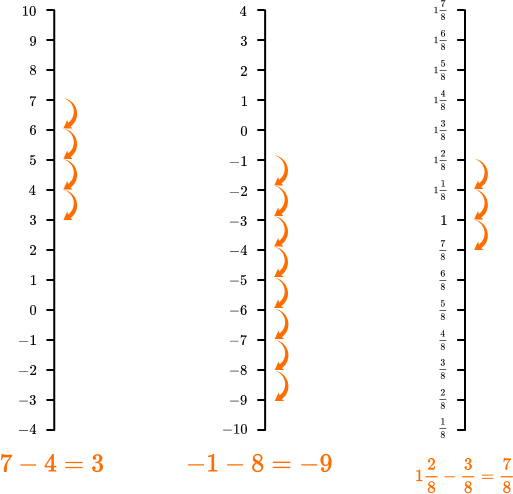
In order to solve subtraction problems with larger numbers, you can use the standard algorithm.
For example,
89.4-3.1
It is important to consider the place value of each digit and line up the corresponding digits and decimal place in each number.
Multiplication
Multiplication is essentially repeated addition.
If you have n copies of a, you multiply a by n to find how many are in the new set, m.
This is the same as calculating a+a+a+… \, n times.
This would be written as n\times{a}=m and pronounced n times a is equal to m.
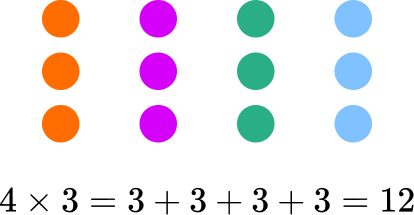
The product is the answer you get when multiplying one number by another. The multiplicand is the quantity to be multiplied by the multiplier, which will give you a product.
multiplicand \times multiplier = product
For example,
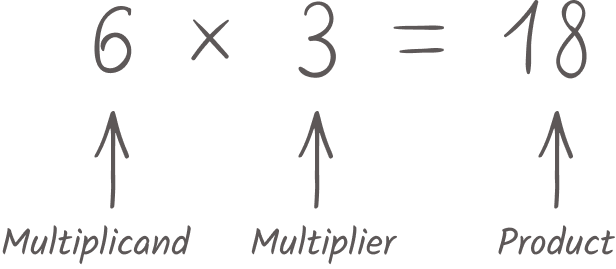
In this calculation,
6 is the multiplicand, 3 is the multiplier and the answer, 18 is the product.
The product will be 0 if either the multiplicand or multiplier is 0.
Multiplication is commutative. The order in which the calculation is performed does not matter.
For example,
3\times{4}=4\times{3}=12Multiplication can be done with positive and negative integers, fractions, and decimals. When multiplying positive and negative numbers, the following rules apply:
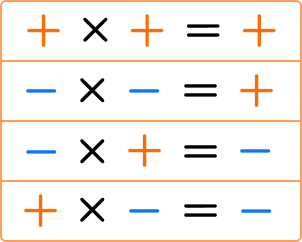
To solve multiplication problems with larger numbers, you can use an area model.
For example,
27 \times 35
Division
Division shares or breaks a number into equal sized numbers of groups.
If the number m can be shared equally between n groups, with no remainder, then this is written as m\div{n}=a and pronounced m divided by n is equal to a.
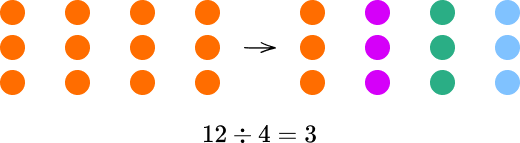
The quotient is the answer you get when dividing one number by another.
The word quotient comes from Latin and means ‘how many times’. When dividing, you are finding out ‘how many times’ a number goes into another number.
dividend \div divisor = quotient
For example,
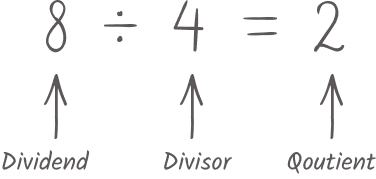
In this calculation,
8 is the dividend, 4 is the divisor and the answer, 2 is the quotient.
The quotient will only be 0 if the dividend is 0 but the divisor is not.
For example,
0 \div 8 = 0Unlike multiplication, division is not commutative. If the order of the numbers within the calculation changes, the result will change.
12\div{4}
Division can also be done with positive and negative integers, fractions, and decimals. When dividing positive and negative numbers, the following rules apply:
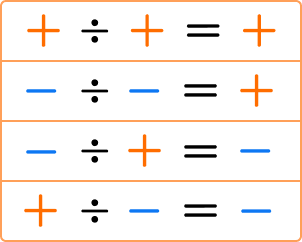
To perform division problems with larger numbers, you can use long division.
For example,
452.1 \div 3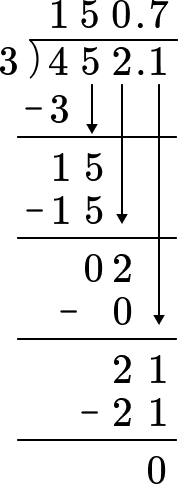
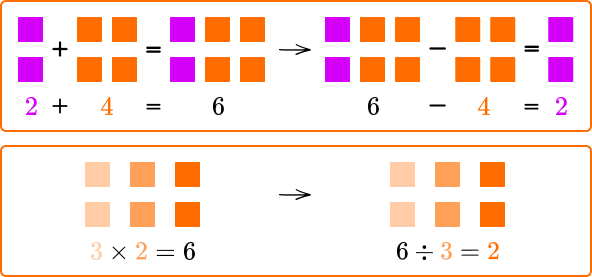
Inverse operations
Inverse operations reverse an operation that has been carried out. Below is a table outlining some operations along with their inverse operations.
| Operation | Inverse Operation |
|---|---|
| Addition (+) | Subtraction (-) |
| Multiplication (\times) | Division (\div) |
Note that you can switch the columns so the inverse operation of subtraction is addition and the inverse operation of division is multiplication, etc.
Using the inverse operations helps us see relationships between numbers and are often referred to as fact families. Fact families show the relationship between the same set of numbers, just as inverse operations do.
Step-by-step guide: Inverse operations (coming soon)
PEMDAS
When solving problems involving basic arithmetic operations, it is important to apply the order of operations, or PEMDAS. PEMDAS tells us what order to perform the operations in.
Parentheses
Exponents
Multiplication
Division
Addition
Subtraction
In the calculation
3+4 \times 2,multiplication should be done before the addition.
3+4 \times 2=3+8=11What is arithmetic?
Common Core State Standards
How does this relate to 4th, 5th, and 6th grade math?
- Grade 4: Number and Operations in Base 10 (4.NBT.4)
Fluently add and subtract multi-digit whole numbers using the standard algorithm.
- Grade 5: Number and Operations in Base Ten (5.NBT.5)
Fluently multiply multi-digit whole numbers using the standard algorithm.
- Grade 5: Number and Operations – Fractions (5.NF.1)
Add and subtract fractions with unlike denominators (including mixed numbers) by replacing given fractions with equivalent fractions in such a way as to produce an equivalent sum or difference of fractions with like denominators.
- Grade 5: Number and Operations – Fractions (5.NF.4)
Apply and extend previous understandings of multiplication to multiply a fraction or whole number by a fraction.
- Grade 6: The Number System (6.NS.1)
Interpret and compute quotients of fractions, and solve word problems involving division of fractions by fractions, example, by using visual fraction models and equations to represent the problem.
- Grade 6: The Number System (6.NS.2)
Fluently divide multi-digit numbers using the standard algorithm.
- Grade 6: The Number System (6.NS.3)
Fluently add, subtract, multiply, and divide multi-digit decimals using the standard algorithm for each operation.
- Grade 6: The Number System (6.NS.5)
Understand that positive and negative numbers are used together to describe quantities having opposite directions or values (example, temperature above/below zero, elevation above/below sea level, credits/debits, positive/negative electric charge); use positive and negative numbers to represent quantities in real-world contexts, explaining the meaning of 0 in each situation.
- Grade 7: The Number System (7.NS.A.1)
Apply and extend previous understandings of addition and subtraction to add and subtract rational numbers; represent addition and subtraction on a horizontal or vertical number line diagram.
- Grade 7: The Number System (7.NS.A.2)
Apply and extend previous understandings of multiplication and division and of fractions to multiply and divide rational numbers.
How to use arithmetic with positive and negative numbers
In order to use arithmetic with positive and negative numbers:
- Determine which operation you will use.
- Perform the chosen operation.
Arithmetic examples
Example 1: addition with decimals
Calculate the value of 10.9+34.3.
- Determine which operation you will use.
Here you will use addition.
2Perform the chosen operation.
Using the standard algorithm, you have:

Starting on the right, the tenths place, you add 9+3=12. The tenths column value of 2 is placed below the answer line, and the 1 is carried above the addition problem, so that you can add it to the next column total (the units column).
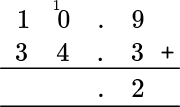
Adding 0, 4, and the 1 that was carried from the tenths column, you have 0+4+1=5 and so 5 goes into the answer bar for the units column.
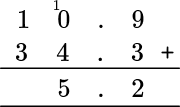
The final column requires us to add 1 and 3, \, 1+3=4 and so you put a 4 in the tens column.
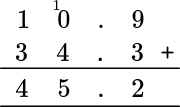
So 10.9+34.3=45.2.
Example 2: subtraction (word problem)
96 mathematicians attended a celebration party at a hotel. 38 mathematicians stayed overnight. How many mathematicians did not stay overnight?
Determine which operation you will use.
Here you will use subtraction. You need to solve 96-38.
Perform the chosen operation.
Writing subtraction using the standard algorithm, you have:
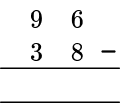
Starting from the units column, 6-8 is a negative number, so you have to borrow from the tens column.
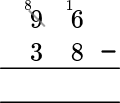
16-8=8 and so the value for the units column is 8.
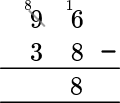
Continuing with the tens column, you have 8-3=5.
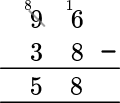
58 guests did not stay overnight.
Example 3: multiplication (word problem)
A sack can hold 36 potatoes. A farmer packs 24 sacks of potatoes with no leftover potatoes. How many potatoes does the farmer pack?
Determine which operation you will use.
As there are 36 potatoes per sack and 24 sacks, you will multiply these values.
Perform the chosen operation.
Using the area model, you have:

By multiplying each row value by each column value, you get:

Adding the new values in the area model, you have:

The farmer packs 864 potatoes.
Example 4: division (word problem)
A bar of chocolate is made up of 84 individual cubes. The bar is 6 cubes wide. How many rows does the chocolate bar have?
Determine which operation you will use.
Each column contains 6 cubes and there are 84 cubes in total. You will need to divide 84 by 6 to determine the number of rows in the chocolate bar.
Perform the chosen operation.
Using partial quotients, you have:
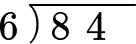
You will think of a multiple of 6 that will get you as close to 84, without going over.
6 \times 10=60
84-60=24
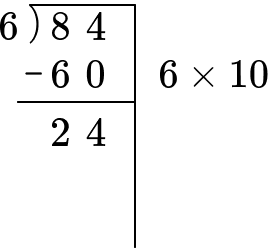
You will think of another multiple of 6 that will get you as close to 24 as possible, without going over.
\begin{aligned} & 6 \times 4=24 \\\\ & 24-24=0 \end{aligned}
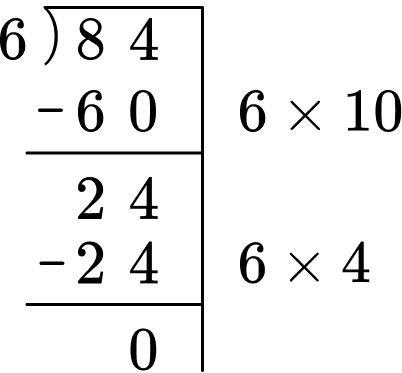
You will add your two partial quotients together 10 + 4 = 14.
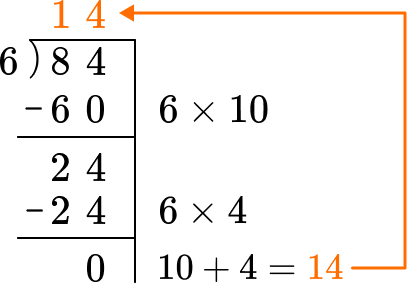
The chocolate bar has 14 rows.
Example 5: addition, with negative numbers
Calculate (-3)+(-2).
Determine which operation you will use.
Here, you are solving an addition problem with the two negative numbers.
Perform the chosen operation.
+ and - together make a - therefore
-3+-2=-3-2=-5
Example 6: subtraction, with negative numbers
Calculate 5-(-3).
Determine which operation you will use.
Here you will subtract -3 from 5.
Perform the chosen operation.
Two - signs together make a + therefore
5--3=5+3=8
Example 7: multiplication, with negative numbers
Calculate 8\times(-2).
Determine which operation you will use.
Here you will use multiplication.
Perform the chosen operation.
8\times(-2)=-16.
Example 8: division, with negative numbers
Calculate \cfrac{-120}{-3}.
Determine which operation you will use.
A fraction is the division of two quantities and so here you would use division. The numerator is known as the dividend and the denominator is known as the divisor. The result of division is called a quotient.
Perform the chosen operation.
Teaching tips for arithmetic
- If a student is struggling with using algorithms with the given operation, they need more experience with concrete models.
- When teaching students to use the algorithm for division, or long division, provide graph paper for students to use to keep their work neat and legible.
- Be sure to practice a problem solving method when working with word problems. Students may be able to solve a given equation, but struggle when having to pull information out of and comprehend a word problem.
- The use of a number line can be very impactful when working with positive and negative numbers.
Easy mistakes to make
- Parentheses are not an arithmetic operation
Operations allow us to perform calculations between two or more numbers. In the associative property, parentheses dictate the order in which this should be completed and so they are technically not an operation. However, parentheses are sometimes used in place of multiplication symbols, for example, 6(7-3).
- Multiplying by \bf{0} by any number equals \bf{0}
It is important to remember that multiplying anything by 0 gives the answer 0.
- Multiplying, instead of dividing, when working with fractions
Mistakes can easily be made when dividing fractions. When dividing a number by a fraction, a commonly seen error is that the value is multiplied by the fraction instead. For example, 12\div\frac{1}{2}=6 is incorrect. Instead, the correct answer is 12\div\frac{1}{2}=12\times{2}=24.
- Knowing the value of decimal places are important
It’s important that students remember the concept of place value when solving with decimals. Knowing the value of the numbers you are performing an operation with is crucial.
Practice arithmetic questions
1. Calculate 8.4+10.7.




Stack the numbers, lining up the decimal points and place values.

Add from right to left, regrouping when necessary.
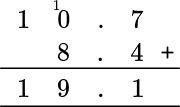
The answer is 19.1.
2. I bought an item for \$25.13. How much change did I get from \$30?




Stack the numbers, the larger number on top, lining up the decimal points and place values.

Subtract from right to left, regrouping when necessary.
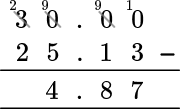
The answer is 4.87.
3. Calculate the 7 th multiple of 9.




List the first multiple of 9 which is 1 \times 9=9.
List the second multiple of 9 which is 2 \times 9=18.
Continue this pattern until you have 7 multiples.
3 \times 9=27
4 \times 9=36
5 \times 9=45
6 \times 9=54
7 \times 9=63
The answer is 63.
4. 120 high school students are divided into small research groups. If there are 20 groups, how many students are in each group?




You need to divide 120 by 20.
You can use mental math to find the solution to this division problem.
You can split the dividend, 120, into two parts that can be easily divided by 20.
120 = 100 + 20
Then using math facts, divide both parts by 20.
100 \div 20=5
20 \div 20=1
120\div{20}=6
5. A New York hotel comprises 67 floors above ground and 4 floors below ground. A guest parks on floor -3, in the basement, and is staying on the 43 rd floor of the hotel. How many floors must he go up to get from his car to his hotel room?




You will subtract 43 and -3.
43- \, -3
Two – signs together make a + therefore,
so 43- \, -3=43+3
43+3 = 46
The answer is 46 floors.
6. Anna buys a car for \$9,000. She pays a deposit of \$2,400 and pays the rest off in monthly installments of \$110 per month. How many months will Anna be paying for her car?
104 months

22 months

60 months

66 months

This is a two-step problem.
The first step requires subtraction to calculate the remaining amount to pay for the car.
The car was \$9,000 and Anna paid a deposit of \$2,400.
9000-2400=6600
The second step will require division of the remaining amount, \$6,600 by 110, the payment Anna will make each month.
6600\div{110}=60
The answer is 60 months.
7. Calculate \cfrac{5}{6}+\cfrac{4}{7}.




First, you will need to find a common denominator between the two fractions. To do this, list the multiples of each number until you find one that both have in common.
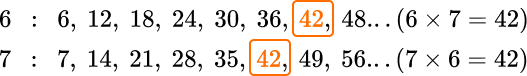
You will also need to fix the numerators by multiplying them by the same factor you multiplied the denominator by.
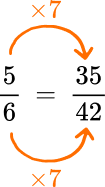
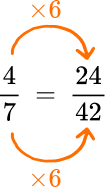
Now that the denominators are the same, you can add the numerators together.
\cfrac{35}{42}+\cfrac{24}{42}=\cfrac{59}{42} \, \text { or } 1 \cfrac{17}{42}
\cfrac{5}{6}+\cfrac{4}{7}=\cfrac{59}{42} \, \text { or } 1 \cfrac{17}{42}
Arithmetic FAQs
Yes, arithmetic is a branch of math that refers to the basic counting of numbers and using operations, such as addition, subtraction, multiplication, and division. Algebra is a branch of math that deals with variables and numbers for solving problems.
A negative number is a number that is less than zero.
The next lessons are
Still stuck?
At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.
Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.

Find out how we can help your students achieve success with our math tutoring programs.
[FREE] Common Core Practice Tests (Grades 3 to 6)
Prepare for math tests in your state with these Grade 3 to Grade 6 practice assessments for Common Core and state equivalents.
40 multiple choice questions and detailed answers to support test prep, created by US math experts covering a range of topics!



