High Impact Tutoring Built By Math Experts
Personalized standards-aligned one-on-one math tutoring for schools and districts
In order to access this I need to be confident with:
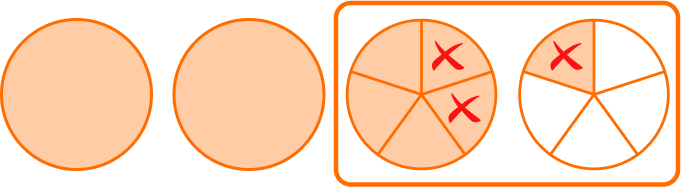
Numerator and denominator Improper fraction to mixed number Fractions of numbers Mixed number to improper fractionAdding and subtracting fractions
Here you will learn about adding and subtracting fractions, including fractions with the same denominator, fractions with different denominators, and mixed numbers.
Students will first learn about adding and subtracting fractions as part of number and operations in fractions in elementary school.
What is adding and subtracting fractions?
Adding and subtracting fractions is when you combine or subtract two or more fractions to find the total or the difference.
To add and subtract fractions, they need a common denominator (bottom number). Then you can add or subtract the fractions by adding or subtracting the numerators (top numbers).
If the fractions have the same denominators already, then the numerators can be easily added or subtracted and the denominator stays the same.
For example,
\cfrac{5}{8}-\cfrac{1}{8}=
The equation is taking \cfrac{1}{8} away from \cfrac{5}{8}.
Since the denominators are the same, the parts are the same size. You subtract to see how many parts are left: 5-1=4.

There are 4 parts. But what size are the parts? They are still eighths, so the denominator stays the same.

\cfrac{5}{8}=\cfrac{1}{8}=\cfrac{4}{8}
If the fractions have unlike denominators, you use equivalent fractions to create fractions with common denominators.
For example,
\cfrac{2}{9}+\cfrac{2}{3}=

Since the denominators are NOT the same, the parts are NOT the same size. Use equivalent fractions to create a common denominator of 9. Multiply the numerator and denominator of \frac{2}{3} by 3.
\cfrac{2 \; \times \; 3}{3 \; \times \; 3}=\cfrac{6}{9}
\cfrac{2}{9}+\cfrac{6}{9}=
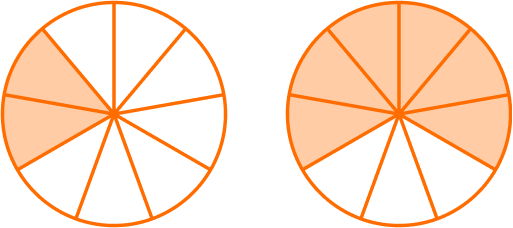
You add to see how many parts there are in total: 2 + 6 = 8.
There are 8 parts. But what size are the parts? They are still ninths, so the denominator stays the same.

\cfrac{2}{9}+\cfrac{2}{3}=\cfrac{8}{9}
Step-by-step guide: Adding fractions
Step-by-step guide: Subtracting fractions
What is adding and subtracting fractions?

Common Core State Standards
How does this relate to 4th grade math and 5th grade math?
- Grade 4 – Number and Operations – Fractions (4.NF.B.3a)
Understand addition and subtraction of fractions as joining and separating parts referring to the same whole.
- Grade 4 – Number and Operations – Fractions (4.NF.B.3c)
Add and subtract mixed numbers with like denominators, e.g., by replacing each mixed number with an equivalent fraction, and/or by using properties of operations and the relationship between addition and subtraction.
- Grade 5 – Number and Operations – Fractions (5.NF.A.1)
Add and subtract fractions with unlike denominators (including mixed numbers) by replacing given fractions with equivalent fractions in such a way as to produce an equivalent sum or difference of fractions with like denominators.
For example, \cfrac{2}{3} + \cfrac{5}{4} = \cfrac{8}{12} + \cfrac{15}{12} = \cfrac{23}{12}. \; ( In general, \cfrac{a}{b} + \cfrac{c}{d} = \cfrac{(ad \; + \; bc)}{bd}.)
How to add and subtract fractions
In order to add or subtract fractions with like denominators:
- Add or subtract the numerators (top numbers).
- Write your answer as a fraction.
In order to add or subtract mixed numbers with like denominators:
- Add or subtract the fractions, borrowing if needed.
- Add or subtract the whole numbers.
- Write your answer as a mixed number.
In order to add or subtract fractions with unlike denominators:
- Create common denominators (bottom numbers).
- Add or subtract the numerators (top numbers).
- Write your answer as a fraction.
In order to add or subtract mixed numbers with unlike denominators:
- Create common denominators (bottom numbers).
- Add or subtract the fractions, borrowing if needed.
- Add or subtract the whole numbers.
- Write your answer as a mixed number.
![[FREE] Fraction Operations Check for Understanding Quiz (Grade 4 to 6)](https://thirdspacelearning.com/wp-content/uploads/2023/07/Fraction-operations-check-for-understandin-quiz-listing-image-.png)
[FREE] Fraction Operations Check for Understanding Quiz (Grade 4 to 6)
![[FREE] Fraction Operations Check for Understanding Quiz (Grade 4 to 6)](https://thirdspacelearning.com/wp-content/uploads/2023/07/Fraction-operations-check-for-understandin-quiz-listing-image-.png)
Use this quiz to check your grade 4 to 6 students’ understanding of fraction operations. 10+ questions with answers covering a range of 4th to 6th grade fraction operations topics to identify areas of strength and support!
DOWNLOAD FREE![[FREE] Fraction Operations Check for Understanding Quiz (Grade 4 to 6)](https://thirdspacelearning.com/wp-content/uploads/2023/07/Fraction-operations-check-for-understandin-quiz-listing-image-.png)
[FREE] Fraction Operations Check for Understanding Quiz (Grade 4 to 6)
![[FREE] Fraction Operations Check for Understanding Quiz (Grade 4 to 6)](https://thirdspacelearning.com/wp-content/uploads/2023/07/Fraction-operations-check-for-understandin-quiz-listing-image-.png)
Use this quiz to check your grade 4 to 6 students’ understanding of fraction operations. 10+ questions with answers covering a range of 4th to 6th grade fraction operations topics to identify areas of strength and support!
DOWNLOAD FREEAdding and subtracting fractions examples
Example 1: adding fractions with like denominators
Solve \cfrac{3}{10}+\cfrac{4}{10}.
- Add or subtract the numerators (top numbers).
\cfrac{3}{10}+\cfrac{4}{10}=

Since the denominators are the same, the parts are the same size. You add to see how many parts there are in total: 3 + 4 = 7.
2Write your answer as a fraction.
There are 7 parts. But what size are the parts? They are still tenths, so the denominator stays the same.

\cfrac{3}{10}+\cfrac{4}{10}=\cfrac{7}{10}
Example 2: subtracting fractions with like denominators
Solve \cfrac{3}{4}-\cfrac{1}{4}.
Add or subtract the numerators (top numbers).
The equation is taking \cfrac{1}{4} away from \cfrac{3}{4}.
Since the denominators are the same, the parts are the same size. You subtract to see how many parts are left: 3-1=2.

Write your answer as a fraction.
There are 2 parts. But what size are the parts? They are still fourths, so the denominator stays the same.

\cfrac{3}{4}-\cfrac{1}{4}=\cfrac{2}{4}
You can also write this answer as the equivalent fraction \cfrac{1}{2}.
Example 3: adding mixed numbers with like denominators
Solve 2 \cfrac{4}{6}+3 \cfrac{5}{6}.
Add or subtract the whole numbers.

2 + 3 = 5
Add or subtract the fractions.
Since the denominators are the same, the parts are the same size. You add to see how many parts there are in total: 4+5=9.
There are 9 parts. But what size are the parts? They are still sixths, so the denominator stays the same.
Since the numerator is greater than the denominator, this is an improper fraction, or a fraction greater than one. We can convert this fraction to a mixed number.
\cfrac{4}{6}+\cfrac{5}{6}=\frac{9}{6} or 1 \cfrac{3}{6}
Write your answer as a mixed number.
Add the whole numbers and fraction together.

5+1 \cfrac{3}{6}=6 \cfrac{3}{6}
You can also write this answer as the equivalent mixed number 6\cfrac{1}{2}.
Example 4: subtracting mixed numbers with like denominators
Solve 3 \cfrac{1}{5}-1 \cfrac{3}{5}.
Add or subtract the fractions, borrowing if needed.
The equation is taking 1 \cfrac{3}{5} away from 3 \cfrac{1}{5}.
Start with the fractions. Since the denominators are the same, the parts are the same size. However, there are not enough parts to take 3 away from 1.
You can break one of the wholes into \cfrac{5}{5}…
3 \cfrac{1}{5}=2 \cfrac{6}{5}
Now you can solve 2 \cfrac{6}{5}-1 \cfrac{3}{5}.
You subtract to see how many parts are left: 6-3=3.
There are 3 parts. But what size are the parts? They are still fifths, so the denominator stays the same.

\cfrac{6}{5}-\cfrac{3}{5}=\cfrac{3}{5}
Add or subtract the whole numbers.

2-1=1
Write your answer as a mixed number.
2 \cfrac{6}{5}-1 \cfrac{3}{5}=1 \cfrac{3}{5}
Example 5: adding fractions with unlike denominators
Solve \cfrac{7}{8}+\cfrac{1}{3}.
Create common denominators (bottom numbers).
\cfrac{7}{8}+\cfrac{1}{3}=

Since \cfrac{7}{8} and \cfrac{1}{3} do not have like denominators, the parts are NOT the same size.
Use equivalent fractions to create a common denominator. Multiply each fraction by the opposite denominator.
\cfrac{7}{8}=\cfrac{7 \; \times \; 3}{8 \; \times \; 3}=\cfrac{21}{24} \quad and \quad \cfrac{1}{3}=\cfrac{1 \; \times \; 8}{3 \; \times \; 8}=\cfrac{8}{24}

Add or subtract the numerators (top numbers).
Since the denominators are the same, the parts are the same size. You add to see how many parts there are in total: 21 + 8 = 29.
\cfrac{21}{24}+\cfrac{8}{24}=

Write your answer as a fraction.
There are 29 parts. But what size are the parts? They are still twenty-fourths, so the denominator stays the same.
\cfrac{21}{24}+\cfrac{8}{24}=\cfrac{29}{24} or 1 \cfrac{5}{24}
Example 6: subtracting fractions with unlike denominators
Solve \cfrac{5}{6}-\cfrac{1}{2}.
Create common denominators (bottom numbers).
Since \cfrac{5}{6} and \cfrac{1}{2} do not have like denominators, the parts are NOT the same size.
A common denominator of 6 can be used. Multiply the numerator and denominator of \cfrac{1}{2} by 3 to create an equivalent fraction.
\cfrac{5}{6} \quad and \quad \cfrac{1 \; \times \; 3}{2 \; \times \; 3}=\cfrac{3}{6}
Add or subtract the numerators (top numbers).
Now use the equivalent fraction to solve: \cfrac{5}{6}-\cfrac{3}{6}.
Since the denominators are the same, the parts are the same size. You subtract to see how many parts are left: 5-3=2.

Write your answer as a fraction.
There are 2 parts. But what size are the parts? They are still sixths, so the denominator stays the same.

\cfrac{5}{6}-\cfrac{3}{6}=\cfrac{2}{6}
You can also write this answer as the equivalent fraction \cfrac{1}{3}.
Example 7: adding mixed numbers with unlike denominators
Solve 1 \cfrac{2}{4}+1 \cfrac{5}{12}.
Add or subtract the whole numbers.
1 + 1 = 2
Create common denominators (bottom numbers).
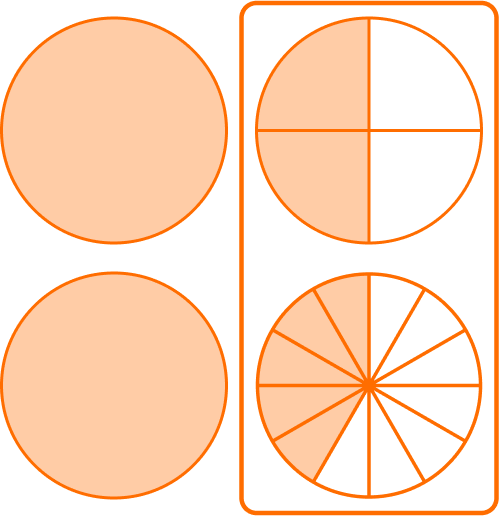
Since \cfrac{2}{4} and \cfrac{5}{12} do not have like denominators, the parts are NOT the same size.
Use equivalent fractions to create a common denominator.
A common denominator of 12 can be used. Multiply the numerator and denominator of \cfrac{2}{4} by 3 to create an equivalent fraction.
\cfrac{2}{4}=\cfrac{2\; \times \; 3}{4 \; \times \; 3}=\cfrac{6}{12} \quad and \quad \cfrac{5}{12}
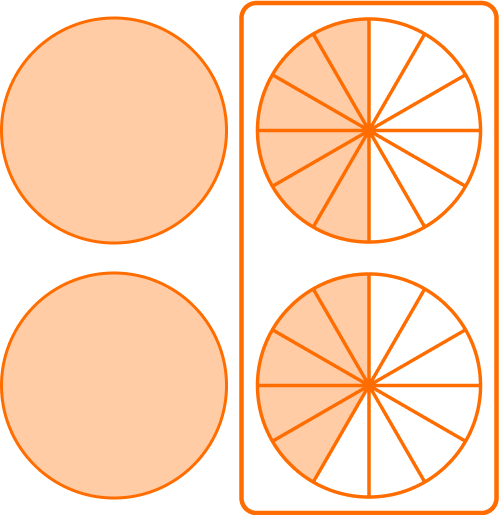
Add or subtract the fractions.
Since the denominators are the same, the parts are the same size. You add to see how many parts there are in total: 6 + 5 = 11.

There are 11 parts. But what size are the parts? They are still twelfths, so the denominator stays the same.
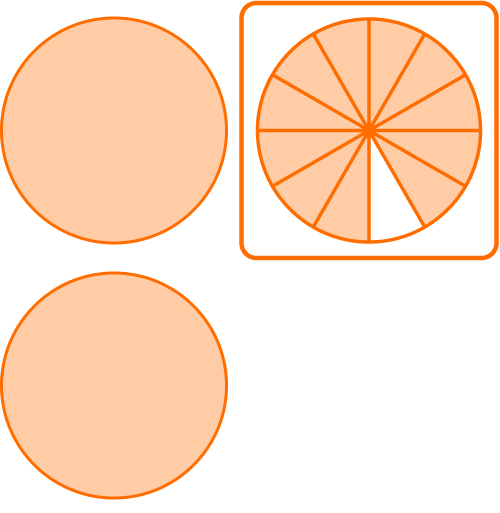
\cfrac{6}{12}+\cfrac{5}{12}=\cfrac{11}{12}
Write your answer as a mixed number.
Add the whole number and fraction together.

2+\cfrac{11}{12}=2 \cfrac{11}{12}
Example 8: subtracting mixed numbers with unlike denominators
Solve 2 \cfrac{8}{10}-1 \cfrac{2}{3}.
Create common denominators (bottom numbers).
The equation is taking 1 \cfrac{2}{3} away from 2 \cfrac{8}{10}.
Start with the fractions. Since \cfrac{8}{10} and \cfrac{2}{3} do not have like denominators, the parts are NOT the same size.
Multiply the numerator and denominator by the opposite denominator to create equivalent fractions with common denominators.
\cfrac{8 \; \times \; 3}{10 \; \times \; 3}=\cfrac{24}{30} \quad and \quad \cfrac{2 \; \times \; 10}{3 \; \times \; 10}=\cfrac{20}{30}
Add or subtract the fractions, borrowing if needed.
Now use the equivalent fractions to solve: 2 \cfrac{24}{20}-1 \cfrac{20}{30}.
Start with the fractions. Since the denominators are the same, the parts are the same size. You subtract to see how many parts are left: 24-20=4.

There are 4 parts. But what size are the parts? They are still thirtieths, so the denominator stays the same.

\cfrac{24}{30}-\cfrac{20}{30}=\cfrac{4}{30}
Add or subtract the whole numbers.

2-1=1
Write your answer as a mixed number.

2 \cfrac{24}{30}-1 \cfrac{20}{30}=1 \cfrac{4}{30}
You can also write this answer as the equivalent mixed number 1\cfrac{2}{15}.
Teaching tips for adding and subtracting fractions
- Fraction work in 3rd grade focuses on understanding through models, including area models and number lines. To continue this in 4th grade and 5th grade, always have digital or physical models available for students to use as a solving strategy.
- When introducing this topic, pose a fraction addition or subtraction problem to students and let them solve it in a way that makes sense to them. Then, as a whole group, let students share the ways they solved the problem, allowing the class to see other ways to solve and make connections between strategies.
- When starting this topic, stick to smaller fractions or problems that do not involve borrowing or regrouping. However, at some point students will need to get used to solving all kinds of fraction subtraction problems mixed together. This lets them learn to identify which solving strategies work best in different situations.
- Fraction worksheets can be useful when students are developing understanding around addition and subtraction, but once students have a successful strategy and can flexibly operate, incorporate math games or real world projects that allow students to add fractions and subtract fractions in a variety of situations.
Our favorite mistakes
- Adding or subtracting the denominators
The denominator tells us how big the parts are. You keep the denominator (the size of the parts) the same and add or subtract the number of parts (numerators).
For example,
- Adding or subtracting without like denominators
Fractions must have like denominators when being added or subtracted. Use equivalent fractions to create a common denominator before adding or subtracting fractions with unlike denominators.
For example,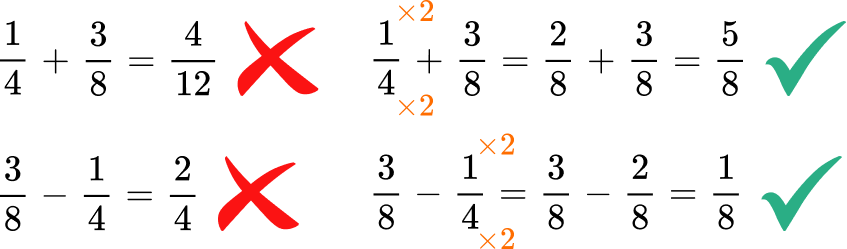
- Forgetting to multiply the numerator when creating an equivalent fraction
To create a fraction with an equivalent value, both the numerator and the denominator need to be multiplied by the same number. Multiplying just one changes the value of the fraction.
For example,
Practice adding and subtracting fractions questions
1. Solve \cfrac{5}{6}+\cfrac{2}{6}.





Since the denominators are the same, the parts are the same size. You add to see how many parts there are in total: 5 + 2 = 7.
There are 7 parts. But what size are the parts? They are still sixths, so the denominator stays the same.

\cfrac{5}{6}+\cfrac{2}{6}=\cfrac{7}{6} or 1 \cfrac{1}{6}
2. Solve \cfrac{11}{12}-\cfrac{4}{12}.




The equation is taking \cfrac{4}{12} away from \cfrac{11}{12}.
Since the denominators are the same, the parts are the same size. You subtract to see how many parts are left: 11-4=7.

There are 7 parts. But what size are the parts? They are still twelfths, so the denominator stays the same.

\cfrac{11}{12}-\cfrac{4}{12}=\cfrac{7}{12}
3. Solve 3 \cfrac{3}{8}+4 \cfrac{6}{8}.




First, add the whole numbers

3 + 4 = 7
Since the denominators are the same, the parts are the same size. You add to see how many parts there are in total: 3 + 6 = 9.

There are 9 parts. But what size are the parts? They are still eighths, so the denominator stays the same.

\cfrac{3}{8}+\cfrac{6}{8}=\cfrac{9}{8} or 1 \cfrac{1}{8}
Add the whole numbers and fraction together.

7+1 \cfrac{1}{8}=8 \cfrac{1}{8}
4. Solve 3 \cfrac{4}{10}-1 \cfrac{9}{10}.




The equation is taking 1 \cfrac{9}{10} away from 3 \cfrac{4}{10}.
Start with the fractions. Since the denominators are the same, the parts are the same size. However, there are not enough parts to take 9 away from 4.
You can break one of the wholes into \cfrac{10}{10}…
3 \cfrac{4}{10}=2 \cfrac{14}{10}
Now you can solve 2 \cfrac{14}{10}-1 \cfrac{9}{10}.
You subtract to see how many parts are left: 14-9=5.
There are 5 parts. But what size are the parts? They are still tenths, so the denominator stays the same.

\cfrac{14}{10}-\cfrac{9}{10}=\cfrac{5}{10} or \cfrac{1}{2}
Subtract the whole numbers.

2-1=1
2 \cfrac{14}{10}-1 \cfrac{9}{10}=1 \cfrac{5}{10}
You can also write this answer as the equivalent mixed number 1 \cfrac{1}{2}.
5. Solve \cfrac{3}{4}+\cfrac{2}{5}.





Since \cfrac{3}{4} and \cfrac{2}{5} do not have like denominators, the parts are NOT the same size.
Use equivalent fractions to create a common denominator. Multiply each fraction by the opposite denominator.
\cfrac{3}{4}=\cfrac{3 \; \times \; 5}{4 \; \times \; 5}=\cfrac{15}{20} \quad and \quad \cfrac{2}{5}=\cfrac{2 \; \times \; 4}{5 \; \times \; 4}=\cfrac{8}{20}

Since the denominators are the same, the parts are the same size. You add to see how many parts there are in total: 15 + 8 = 23.
There are 23 parts. But what size are the parts? They are still twentieths, so the denominator stays the same.

\cfrac{15}{20}+\cfrac{8}{20}=\cfrac{23}{20} or 1 \cfrac{3}{20}
6. Solve \cfrac{2}{5}-\cfrac{1}{3}.




Since \cfrac{2}{5} and \cfrac{1}{3} do not have like denominators, the parts are NOT the same size.
Multiply the numerator and denominator by the opposite denominator to create equivalent fractions with common denominators.
\cfrac{2 \; \times \; 3}{5 \; \times \; 3}=\cfrac{6}{15} \quad and \quad \cfrac{1 \; \times \; 5}{3 \; \times \; 5}=\cfrac{5}{15}
Now use the equivalent fractions to solve: \cfrac{6}{15}-\cfrac{6}{15}.
Since the denominators are the same, the parts are the same size. You subtract to see how many parts are left: 6-5=1.
There are 1 part. But what size is the part? It is still a fifteenth, so the denominator stays the same.

\cfrac{6}{15}-\cfrac{5}{15}=\cfrac{1}{15}
7. Solve 1 \cfrac{4}{6}+4 \cfrac{7}{12}.




First, add the whole numbers.

1 + 4 = 5

Since \cfrac{4}{6} and \cfrac{7}{12} do not have like denominators, the parts are NOT the same size. A common denominator of 12 can be used.
Multiply the numerator and denominator of \cfrac{4}{6} by 2 to create an equivalent fraction.
\cfrac{4}{6}=\cfrac{4 \; \times \; 2}{6 \; \times \; 2}=\cfrac{8}{12} \quad and \quad \cfrac{7}{12}

Since the denominators are the same, the parts are the same size. You add to see how many parts there are in total: 8 + 7 = 15.
You have 15 parts. But what size are the parts? They are still twelfths, so the denominator stays the same.

\cfrac{8}{12}+\cfrac{7}{12}=\cfrac{15}{12} or 1 \cfrac{3}{12}
Add the whole numbers and fraction together.

5+1 \cfrac{3}{12}=6 \cfrac{3}{12}
You can also write this answer as the equivalent mixed number 6 \cfrac{1}{4}.
8. Solve 4 \cfrac{5}{8}-3 \cfrac{2}{3}.




The equation is taking 3\cfrac{2}{3} away from 4\cfrac{5}{8}.
Start with the fractions. Since \cfrac{5}{8} and \cfrac{2}{3} do not have like denominators, the parts are NOT the same size. Use equivalent fractions to create a common denominator.
Multiplying the numerator and denominator by the opposite denominator will create common denominators.
\cfrac{5 \; \times \; 3}{8 \; \times \; 3}=\cfrac{15}{24} \quad and \quad \cfrac{2 \; \times \; 8}{3 \; \times \; 8}=\cfrac{16}{24}
Now use the equivalent fraction to solve: 4 \cfrac{15}{24}-3 \cfrac{16}{24}.
Start with the fractions. Since the denominators are the same, the parts are the same size. However, there are not enough parts to take 16 away from 15.
You can break one of the wholes into \cfrac{24}{24}…
4 \cfrac{15}{24}=3 \cfrac{39}{24}

Now you can solve 3 \cfrac{39}{24}-3 \cfrac{16}{24}.
You subtract to see how many parts are left: 39-16 = 23.

There are 23 parts left. But what size are the parts? They are still twenty-fourths, so the denominator stays the same.

\cfrac{39}{24}-\cfrac{16}{24}=\cfrac{23}{24}
Subtract the whole numbers.

3-3=0

3 \cfrac{39}{24}-3 \cfrac{16}{24}=\cfrac{23}{24}
Adding and subtracting fractions FAQs
No, although after multiplying or dividing the numerator and the denominator are new numbers, the value of the fraction remains the same. If the new fraction has a larger denominator, the parts will be smaller, so the numerator also needs to be larger so that the proportion of the parts is the same as the original fraction. If the new fraction has a smaller denominator, the parts will be larger, so the numerator also needs to be smaller so that the proportion of the parts is the same as the original fraction.
No, students do not have to find the least common denominator in order to correctly answer a fraction addition or subtraction question. However, as students progress in their understanding of fractions, you can encourage students to utilize this skill. Also be mindful of standard expectations, as they may vary from state to state.
The next lessons are
Still stuck?
At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.
Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.

Find out how we can help your students achieve success with our math tutoring programs.
[FREE] Common Core Practice Tests (3rd to 8th Grade)
Prepare for math tests in your state with these 3rd Grade to 8th Grade practice assessments for Common Core and state equivalents.
Get your 6 multiple choice practice tests with detailed answers to support test prep, created by US math teachers for US math teachers!