[FREE] Fun Math Games & Activities Packs
Always on the lookout for fun math games and activities in the classroom? Try our ready-to-go printable packs for students to complete independently or with a partner!
In order to access this I need to be confident with:
Whole numbers Adding fractions Multiplying and dividing fractions Converting fractions, decimals, and percentagesMixed number to improper fraction
Here you will learn about converting a mixed number to an improper fraction, including how to recognize improper fractions and mixed numbers.
Students will first learn how to convert a mixed number to an improper fraction as part of number and operations – fractions in 4th grade.
What are mixed numbers and improper fractions?
Mixed numbers and improper fractions are types of numbers that have wholes and parts.
A mixed number is written with a whole number part and a fractional part.
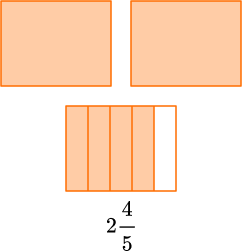
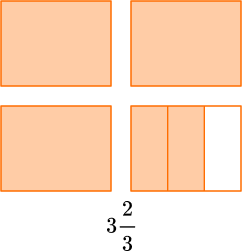
For example,

Now let’s look at two types of fractions: proper and improper fractions.
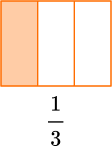
A proper fraction is a fraction where the numerator (top number) is less than the denominator (bottom number).
For example,
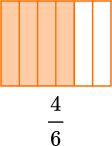

An improper fraction is a fraction where the numerator (top number) is greater than the denominator (bottom number).
For example,
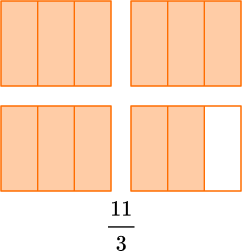

Mixed numbers and improper fraction can both be used to show numbers that are larger than 1.
For example,
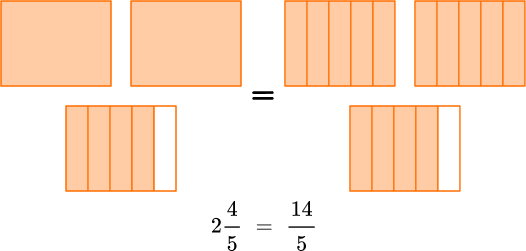
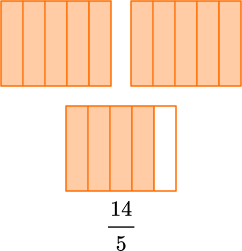
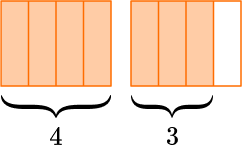
2 \cfrac{4}{5} \, is 2 and \cfrac{4}{5}, which is two wholes and a group of \cfrac{4}{5}.
\cfrac{14}{5} \, is 14 fifths, which is two groups of \cfrac{5}{5} and a group of \cfrac{4}{5}.
What are mixed numbers and improper fractions?

Common Core State Standards
How does this relate to 4th grade math?
- Grade 4 – Numbers and Operations – Fractions (4.NF.B.3c)
Add and subtract mixed numbers with like denominators, for example, by replacing each mixed number with an equivalent fraction and/or by using properties of operations and the relationship between addition and subtraction.
![[FREE] Mixed Numbers to Improper Fractions Worksheet (Grade 4 to 5)](https://thirdspacelearning.com/wp-content/uploads/2023/11/Mixed-Numbers-to-Improper-Fractions-Worksheet-listing-image.png)
[FREE] Mixed Numbers to Improper Fractions Worksheet (Grade 4 to 5)
![[FREE] Mixed Numbers to Improper Fractions Worksheet (Grade 4 to 5)](https://thirdspacelearning.com/wp-content/uploads/2023/11/Mixed-Numbers-to-Improper-Fractions-Worksheet-listing-image.png)
Use this worksheet to check your grade 4 to 5 students’ understanding of mixed numbers to improper fractions. 15 questions with answers to identify areas of strength and support!
DOWNLOAD FREE![[FREE] Mixed Numbers to Improper Fractions Worksheet (Grade 4 to 5)](https://thirdspacelearning.com/wp-content/uploads/2023/11/Mixed-Numbers-to-Improper-Fractions-Worksheet-listing-image.png)
[FREE] Mixed Numbers to Improper Fractions Worksheet (Grade 4 to 5)
![[FREE] Mixed Numbers to Improper Fractions Worksheet (Grade 4 to 5)](https://thirdspacelearning.com/wp-content/uploads/2023/11/Mixed-Numbers-to-Improper-Fractions-Worksheet-listing-image.png)
Use this worksheet to check your grade 4 to 5 students’ understanding of mixed numbers to improper fractions. 15 questions with answers to identify areas of strength and support!
DOWNLOAD FREEHow to convert a mixed number to an improper fraction
In order to convert a mixed number to an improper fraction with a model:
- Model the mixed number.
- Split the wholes into equal parts (the same number as the denominator).
- Count the number of fractional parts in all.
- Write the improper fraction.
In order to convert a mixed number to an improper fraction with the algorithm:
- Multiply the denominator by the whole number.
- Add the product to the numerator and keep the same denominator.
- Write the improper fraction.
Convert a mixed number to an improper fraction examples
Example 1: mixed number to an improper fraction with a model
Write the mixed number 1\cfrac{3}{4} \, as an improper fraction.
- Model the mixed number.
Draw 1 whole and \cfrac{3}{4}.

2Split the wholes into equal parts (the same number as the denominator).
The fraction is in fourths, so you split the whole into fourths.

3Count the number of fractional parts in all.
There are 7 parts and they are fourths.
4Write the improper fraction.
1 \cfrac{3}{4}=\cfrac{7}{4}Example 2: mixed number to an improper fraction with a model
Write the mixed number 4\cfrac{5}{6} \, as an improper fraction.
Model the mixed number.
Draw 4 wholes and \cfrac{5}{6}.

Split the wholes into equal parts (the same number as the denominator).
The fraction is in sixths, so you split the wholes into sixths.

Count the number of fractional parts in all.
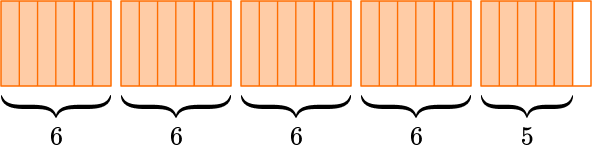
There are 29 parts and they are sixths.
Write the improper fraction.
Example 3: mixed number to an improper fraction with a model
Write the mixed number 3\cfrac{2}{10} \, as an improper fraction.
Model the mixed number.
Draw 3 wholes and \cfrac{2}{10}.

Split the wholes into equal parts (the same number as the denominator).
The fraction is in tenths, so you split the wholes into tenths.

Count the number of fractional parts in all.
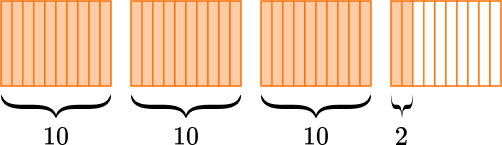
There are 32 parts and they are tenths.
Write the improper fraction.
Example 4: mixed number to an improper fraction with the algorithm
Write the mixed number 2\cfrac{3}{12} \, as an improper fraction.
Multiply the denominator by the whole number.
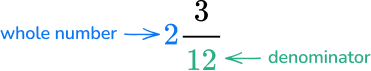
12 \times 2=24
Add the product to the numerator and keep the same denominator.
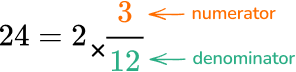
24 + 3 = 27
The new numerator is 27 and the denominator is still 12.
Write the improper fraction.
Example 5: mixed number to an improper fraction with the algorithm
Write the mixed number 6\cfrac{1}{2} \, as an improper fraction.
Multiply the denominator by the whole number.
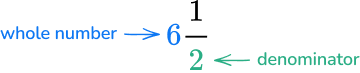
2 \times 6=12
Add the product to the numerator and keep the same denominator.
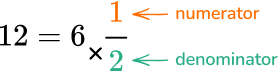
12 + 1 = 13
The new numerator is 13 and the denominator is still 2.
Write the improper fraction.
Example 6: mixed number to an improper fraction with the algorithm
Write the mixed number 9\cfrac{7}{8} \, as an improper fraction.
Multiply the denominator by the whole number.

8 \times 9=72
Add the product to the numerator and keep the same denominator.
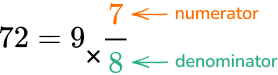
72 + 7 = 79
The new numerator is 79 and the denominator is still 8.
Write the improper fraction.
Teaching tips for converting a mixed number to an improper fraction
- Start this topic by letting students explore their own understanding of mixed numbers and improper fractions. Students will typically do this through models. If students spend enough time thinking about and creating models, the algorithm becomes a logical solving strategy. They realize that multiplying the denominator and the whole number is the same as breaking up the model into equal parts and that the numerator of the improper fraction is the total number of parts.
- When using worksheets, make sure that students have ample room to solve since there are many different ways that students can go about converting from mixed numbers to improper fractions. Students may use different types of models (including number lines and area models) or figure out how to use different equations to solve. They need room to show all of this thinking on paper. Even once students begin to use the algorithm, as it is a two-step process, they will also need adequate room to solve.
Easy mistakes to make
- Adding the whole number to the denominator instead of multiplying
The whole number should be multiplied by the denominator to show the correct number of fractional parts. This is the same as splitting a model into the denominator’s fractional parts. Adding the whole number and the denominator is not the correct process and usually occurs because students misunderstand the algorithm.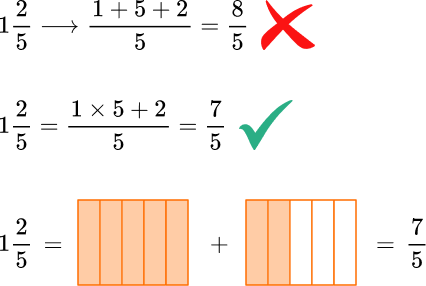
- Confusing mixed numbers and improper fractions
Mixed numbers are written with a whole number and a fractional part. For example, 4 \cfrac{5}{6}.
Improper fractions are not written with a whole number part, but the numerator is always bigger than the denominator. For example, \cfrac{29}{6}.
- Not drawing clear models
Models are only a helpful tool to solve fractions problems if they are drawn clearly. Models also become more difficult for students as the denominators get larger. Splitting shapes into more and more equal parts leaves room for error. It is a good idea to also give students access to a physical or digital model that already has wholes split into fractional parts.
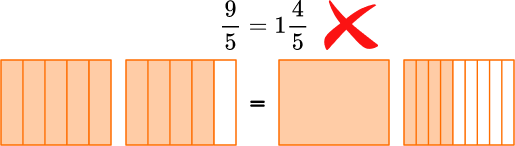
- Not keeping the denominator the same
Any given number in mixed number or improper fraction form should have the same value. This is because the size of the fractional parts does not change, so the denominator for each should be the same. The exception is when a fraction is simplified, which changes the denominator but not the overall value of the mixed number or improper fraction.
For example,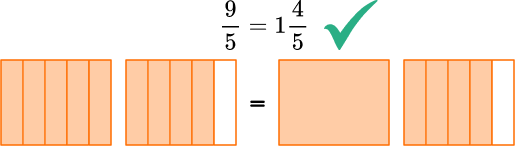
Practice converting a mixed number to an improper fractions questions
1. Write the following mixed number as an improper fraction: 2\cfrac{3}{5}.




Draw 2 wholes and \cfrac{3}{5}.

The fraction is in fifths, so you split the wholes into fifths.

Count the number of fractional parts in all.
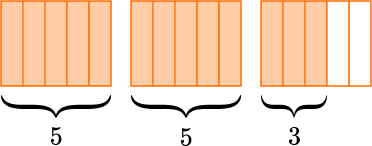
There are 13 parts and they are fifths.
2 \cfrac{3}{5}=\cfrac{13}{5}
2. Write the following mixed number as an improper fraction: 5\cfrac{1}{3}.




Draw 5 wholes and \cfrac{1}{3}.

The fraction is in thirds, so you split the wholes into thirds.

Count the number of fractional parts in all.
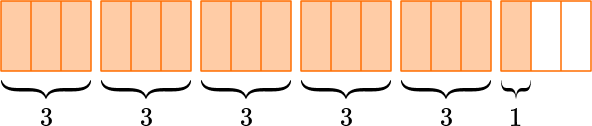
There are 16 parts and they are thirds.
5 \cfrac{1}{3}=\cfrac{16}{3}
3. Write the following mixed number as an improper fraction: 8\cfrac{1}{4}.




Draw 8 wholes and \cfrac{1}{4}.

The fraction is in fourths, so you split the wholes into fourths.

Count the number of fractional parts in all.

There are 33 parts and they are fourths.
8 \cfrac{1}{4}=\cfrac{33}{4}
4. Write the following mixed number as an improper fraction: 5\cfrac{11}{12}.




Multiply the denominator by the whole number.
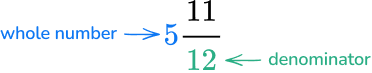
12 \times 5=60
Add the product to the numerator and keep the same denominator.
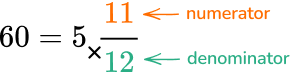
60 + 11 = 71
The new numerator is 71 and the denominator is still 12.
5 \cfrac{11}{12}=\cfrac{71}{12}
5. Write the following mixed number as an improper fraction: 4\cfrac{2}{8}.




Multiply the denominator by the whole number.
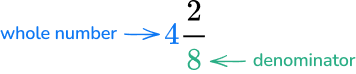
8 \times 4=32
Add the product to the numerator and keep the same denominator.

32 + 2 = 34
The new numerator is 34 and the denominator is still 8.
4 \cfrac{2}{8}=\cfrac{34}{8}
6. Write the following mixed number as an improper fraction: 7\cfrac{5}{6}.




Multiply the denominator by the whole number.
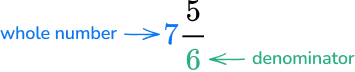
6 \times 7=42
Add the product to the numerator and keep the same denominator.
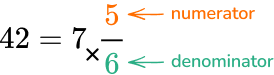
42 + 5 = 47
The new numerator is 47 and the denominator is still 6.
7 \cfrac{5}{6}=\cfrac{47}{6}
Mixed number to improper fraction FAQs
No, this skill does not require students to convert to lowest terms (also known as the simplest form). That said, it is possible that students will be asked to provide an answer in lowest terms. Refer to your state’s standards for specific guidance on when this is appropriate.
Both of these are other names for a mixed number. They mean the same thing.
The next lessons are
Still stuck?
At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.
Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.

Find out how we can help your students achieve success with our math tutoring programs.
[FREE] Common Core Practice Tests (Grades 3 to 6)
Prepare for math tests in your state with these Grade 3 to Grade 6 practice assessments for Common Core and state equivalents.
40 multiple choice questions and detailed answers to support test prep, created by US math experts covering a range of topics!