[FREE] Fun Math Games & Activities Packs
Always on the lookout for fun math games and activities in the classroom? Try our ready-to-go printable packs for students to complete independently or with a partner!
In order to access this I need to be confident with:
Adding and subtracting fractions Natural numbers Whole numbersTypes of fractions
Here you will learn about the types of fractions, including how to model and write numbers as proper and improper fractions and mixed numbers.
Students will first learn about different types of fractions as part of number and operations – fractions in 4th grade.
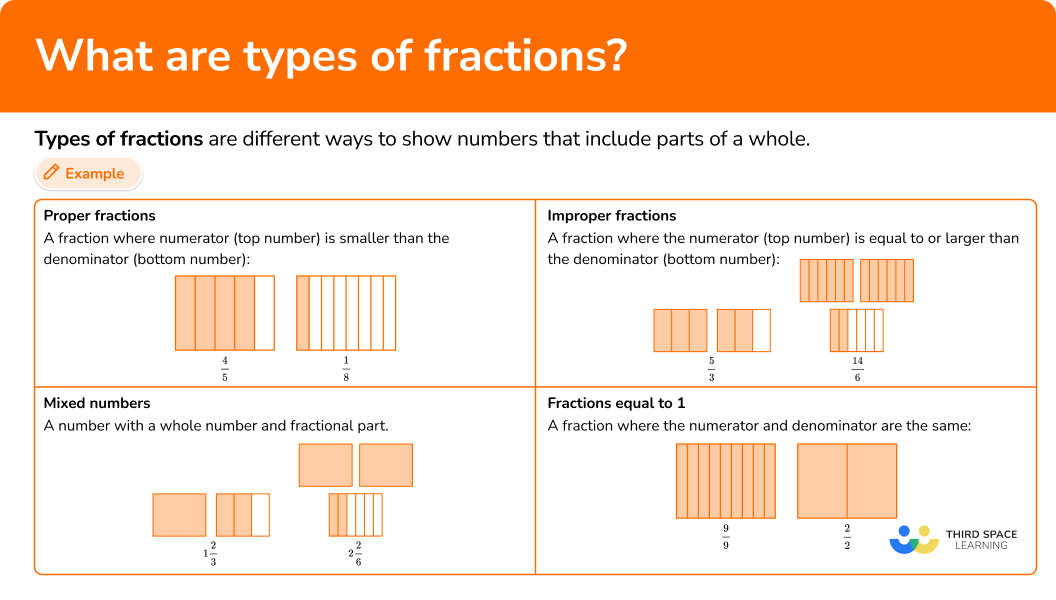
What are types of fractions?
Types of fractions are different ways to show numbers that include parts of a whole. Types of fractions are typically grouped by values that are less than 1 and greater than 1.
For numbers that are less than one, you use proper fractions. In this type of fraction, the numerator (top number) is smaller than the denominator (bottom number).
For example,
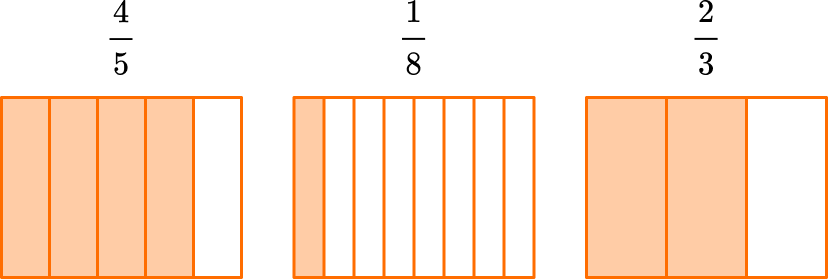
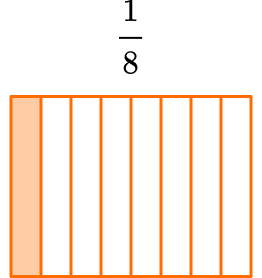
When a proper fraction has a numerator of 1, it is called a unit fraction.
For example,
\cfrac{1}{8} \, is a unit fraction.
When a fraction has the same numerator and denominator, it is equal to \bf{1}.
For example,
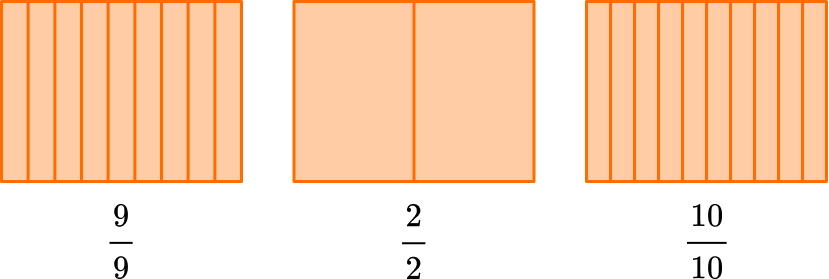
For numbers larger than one, you use improper fractions and mixed numbers.
An improper fraction is a fraction where the numerator (top number) is equal to or larger than the denominator (bottom number).
For example,
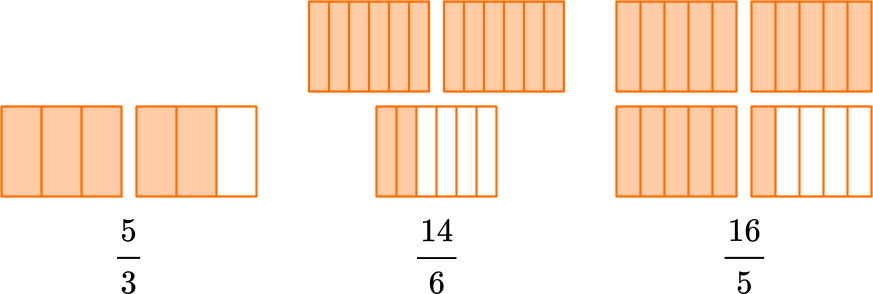
A mixed number has a whole number part and a fractional part. Sometimes mixed numbers are called mixed fractions.
For example,
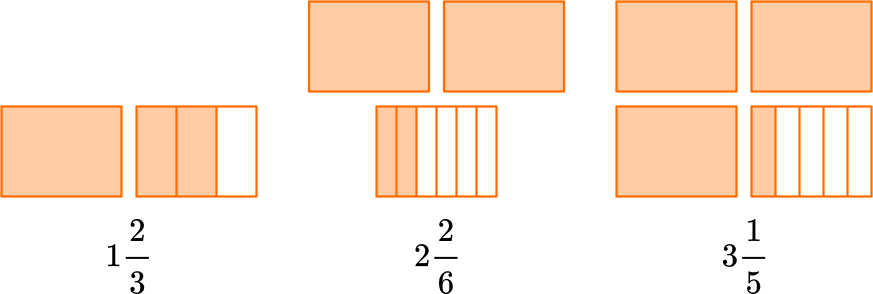
Any number greater than 1 can be shown as an improper fraction AND a mixed number.
For example,
Proper fractions  |
Improper fractions  |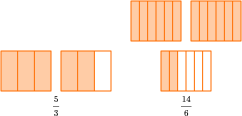
Mixed numbers  |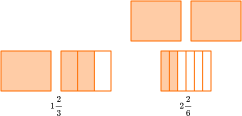
Fractions equal to \bf{1}  |
What are types of fractions?
Common Core State Standards
How does this relate to 4th grade math?
- Grade 4 – Numbers and Operations – Fractions (4.NF.B.3c)
Add and subtract mixed numbers with like denominators, example, by replacing each mixed number with an equivalent fraction, and/or by using properties of operations and the relationship between addition and subtraction.
How to use types of fractions
In order to model and write types of fractions:
- Identify the denominator.
- Decide if the fraction is larger than \bf{1} whole. If it is less, skip to step \bf{4} .
- Decide whether to write the fraction as an improper fraction or a mixed number.
- Write the fraction in the correct form.
![[FREE] Types of Fractions Worksheet (Grade 4 to 5)](https://thirdspacelearning.com/wp-content/uploads/2023/11/Types-of-Fractions-Worksheet-listing-image.png)
[FREE] Types of Fractions Worksheet (Grade 4 to 5)
Use this worksheet to check your grade 4 to 5 students’ understanding of types of fractions. 15 questions with answers to identify areas of strength and support!
DOWNLOAD FREE [FREE] Types of Fractions Worksheet (Grade 4 to 5)
Use this worksheet to check your grade 4 to 5 students’ understanding of types of fractions. 15 questions with answers to identify areas of strength and support!
DOWNLOAD FREETypes of fractions examples
Example 1: write a proper fraction given a model
Write the value shown by the shaded part of the model.
- Identify the denominator.
The model is broken up into 6 equal parts, so 6 is the denominator.
2Decide if the fraction is larger than \bf{1} whole. If it is less, skip to step \bf{4} .
The number is less than 1 whole, skip to step 4.
4Write the fraction in the correct form.
Numbers less than 1 whole, can be written as proper fractions. The numerator is 4, because 4 parts are shaded in.
The model shows the proper fraction \, \cfrac{4}{6} \, shaded in.
Example 2: write a mixed number given a model
Write the value shown by the shaded part of the model.
Identify the denominator.
The last whole in the model is broken up into 9 equal parts, so 9 is the denominator.
Decide if the fraction is larger than \bf{1} whole. If it is less, skip to step \bf{4} .
The value is larger than 1 whole, so move to the next step.
Decide whether to write the fraction as an improper fraction or a mixed number.
The model shows 2 wholes with parts left over, which can be used to write a mixed number.
Write the fraction in the correct form.
The numerator is 5, because 5 parts are shaded in the last whole.
The model shows the mixed number \, 2 \cfrac{5}{9} \, shaded in.
Example 3: write an improper fraction given a model
Write the value shown by the shaded part of the model.
Identify the denominator.
Each whole in the model is broken up into 10 equal parts, so 10 is the denominator.
Decide if the fraction is larger than \bf{1} whole. If it is less, skip to step \bf{4} .
The value is larger than 1 whole, so move to the next step.
Decide whether to write the fraction as an improper fraction or a mixed number.
The model is shown in parts, which can be used to write an improper fraction.
Write the fraction in the correct form.
The numerator is 18, because 18 parts are shaded in.
The model shows the improper fraction \, \cfrac{18}{10}
\, shaded in.
Example 4: create a model given a proper fraction
Show a model of \, \cfrac{3}{8}.
Identify the denominator.
The denominator is 8, so the model should be shown with 8 equal parts.
Decide if the fraction is larger than \bf{1} whole. If it is less, skip to step \bf{4} .
The numerator is less than the denominator, so \, \cfrac{3}{8} \, is a proper fraction and is less than 1 whole. Skip to step 4.
Write the fraction in the correct form.
The numerator is 3, so there should be 3 parts shaded in.
The model shows the proper fraction \, \cfrac{3}{8} \, shaded in.
Example 5: create a model given a mixed number
Show a model of \, 4 \cfrac{1}{4} \, .
Identify the denominator.
The denominator is 4, so the fractional part of the model should be shown with 4 equal parts.
Decide if the fraction is larger than \bf{1} whole. If it is less, skip to step \bf{4} .
The value is larger than 1 whole, so move to the next step.
Decide whether to write the fraction as an improper fraction or a mixed number.
There are 4 wholes with parts left over, so \, 4 \cfrac{1}{4} \, is a mixed number.
Write the fraction in the correct form.
Show 4 wholes shaded, and 1 out of 4 parts shaded for the fractional part.
The model shows the mixed number \, 4 \cfrac{1}{4} \, shaded in.
Example 6: create a model given an improper fraction
Show a model of \, \cfrac{13}{12} \, .
Identify the denominator.
The denominator is 12, so the model should show twelfths.
Decide if the fraction is larger than \bf{1} whole. If it is less, skip to step \bf{4} .
The value is larger than 1 whole, so move to the next step.
Decide whether to write the fraction as an improper fraction or a mixed number.
There are just parts, so \, \cfrac{13}{12} \, is an improper fraction.
Write the fraction in the correct form.
The numerator is 13, so 13 parts should be shown.
The model shows the improper fraction \, \cfrac{13}{12} \, on a number line.
Teaching tips for different types of fractions
- In elementary school, choose worksheets that give students a lot of space to solve when working with any type of fraction. Students should have enough space to draw different types of models (including area models and number lines) or explore different operations and equations when solving problems with fractions.
- Spend time connecting each type of fraction to a real-life situation. This can be as simple as drawing attention to different types of fractions as they appear naturally in the classroom or school setting. Students are more likely to recognize and understand different types of fractions if they have consistent exposure and can make real-life connections.
Easy mistakes to make
- Drawing unclear models
Models are only a useful solving tool if they are drawn correctly. In general, they work better with smaller fractions as larger numerators and denominators leave more room for error. Consider giving students access to an easy to use digital model that creates more complicated fraction pieces for them.
- Not keeping the denominator the same
When converting from a model to a written representation (or vice versa), the denominator should stay the same. Note that the denominator can change when simplifying, but this does not change the overall value of the fraction.
For example,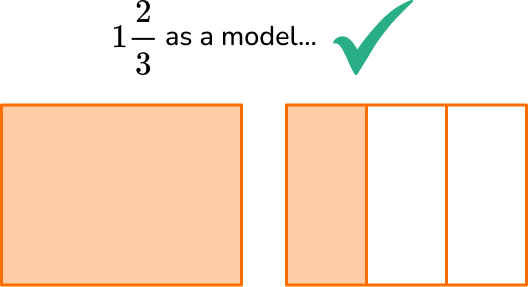
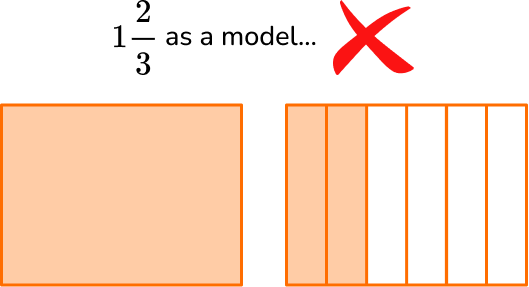
- Including an improper fraction within a mixed number
For a mixed number, the fractional part should be proper. If the fraction is improper, it means that another whole can be created.
For example,
Write the value shown by the shaded part of the model.
It can be written as \, \cfrac{16}{6} \, or \, 2 \cfrac{4}{6} \; {\color{#00ab41}✔} \, , but not \, 1 \cfrac{10}{6}
*The equation is true, but a mixed number should only include a proper fraction.
Practice different types of fractions questions
1. What is the number shown by the shaded part of the model?
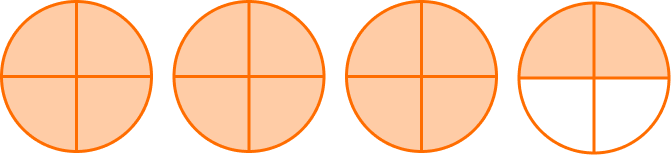
Each whole in the model is broken up into 4 equal parts, so 4 is the denominator.
Numbers greater than 1 whole can be written as improper fractions.
The numerator is 14, because 14 parts are shaded in.
The model shows the improper fraction \, \cfrac{14}{4} \, shaded in.
2. What is the number shown by the shaded part of the model?
The model is broken up into 8 equal parts, so 8 is the denominator.
Numbers less than 1 whole can be written as proper fractions.
The numerator is 2, because 2 parts are shaded in.
The model shows the proper fraction \, \cfrac{2}{8} \, shaded in.
3. What is the number shown by the shaded part of the model?
Numbers greater than 1 whole can be written as mixed numbers.
There are 3 shaded wholes.
The last whole in the model is broken up into 3 equal parts, so 3 is the denominator.
The numerator is 1, because 1 part is shaded in.
The model shows the mixed number \, 3 \cfrac{1}{3} \, shaded in.
4. Which model shows \, \cfrac{11}{6} \, shaded in?
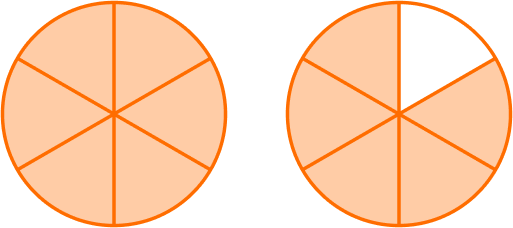
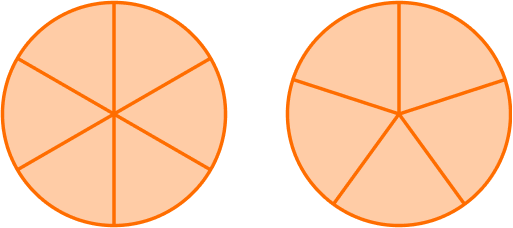
\cfrac{11}{6} \, is an improper fraction.
The denominator is 6, so the model should show 6 equal parts.
The numerator is 11, so there should be 11 parts shaded in.
The model shows \, \cfrac{11}{6} \, shaded in.
5. Which model shows \, 2 \cfrac{3}{10} \, shaded in?
2\cfrac{3}{10} \, is a mixed number.
There are 2 wholes with left over parts.
The denominator is 10, so the last whole should show 10 equal parts.
The numerator is 3, so there should be 3 parts shaded in the last whole.
The model shows \, 2\cfrac{3}{10} \, shaded in.
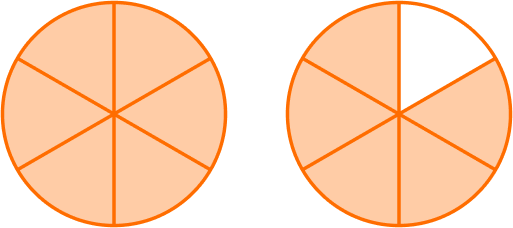
6. Which model shows \, \cfrac{7}{12} \, shaded in?
\cfrac{7}{12} \, is a proper fraction.
The denominator is 12, so the model should show 12 equal parts.
The numerator is 7, so there should be 7 parts shaded in.
The model shows \, \cfrac{7}{12} \, shaded in.
Types of fractions FAQs
The numerator shows the number of parts and the denominator shows the size of the parts.
Students work with all of the fraction types overviewed on this page, which all involve only natural numbers as the numerators and denominators. In middle and high school, they use more advanced topics (like negative numbers and variables) to work with more complex fractions.
Still stuck?
At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.
Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.
Find out how we can help your students achieve success with our math tutoring programs.
[FREE] Common Core Practice Tests (Grades 3 to 6)
Prepare for math tests in your state with these Grade 3 to Grade 6 practice assessments for Common Core and state equivalents.
40 multiple choice questions and detailed answers to support test prep, created by US math experts covering a range of topics!