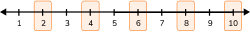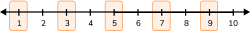High Impact Tutoring Built By Math Experts
Personalized standards-aligned one-on-one math tutoring for schools and districts
Natural numbers
Here you will learn about natural numbers, including the types of natural numbers and properties of natural numbers.
Students will first learn about natural numbers in Kindergarten with counting and cardinality and extend that knowledge through elementary school into middle school with properties of addition and multiplication.
What are natural numbers?
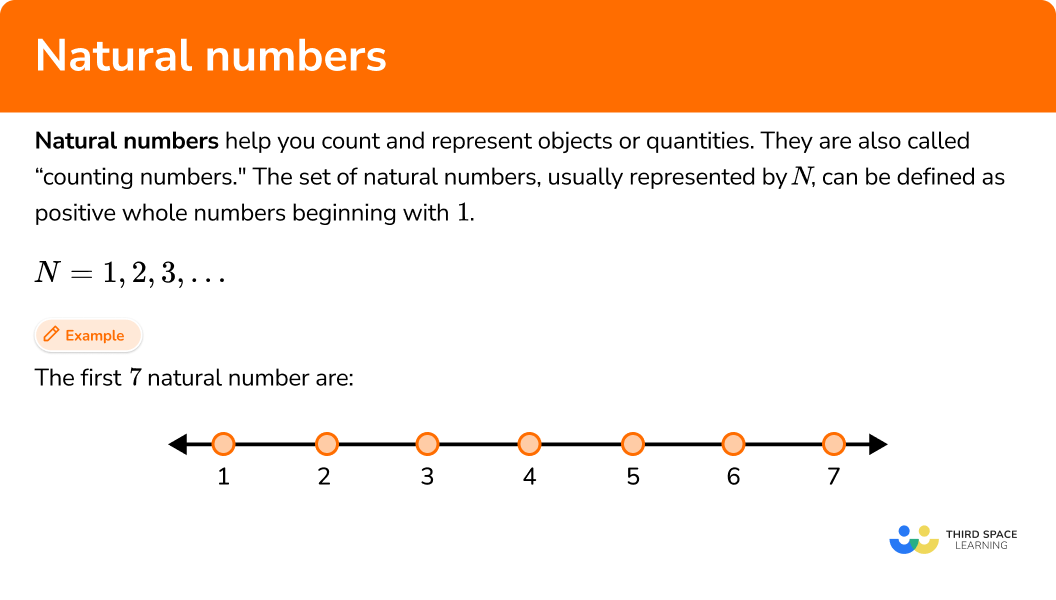
Natural numbers help you count and represent objects or quantities. They are also called “counting numbers”. The set of natural numbers, usually represented by N, can be defined as positive whole numbers beginning with 1.
N = \{1, 2, 3, …\}This number line shows the first 7 natural numbers.

Let’s look at some types of natural numbers and properties of natural numbers.
Prime and Composite Natural Numbers \hspace{1cm}
A prime number is a number with exactly 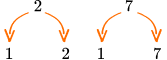 2 has two factors: \hspace{1cm}
7 has two factors:
| A composite number is a number with more 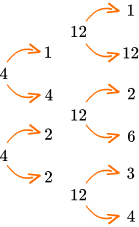 4 has three factors: \hspace{1cm}
12 has six factors:
|
Step-by-step guide: Prime number
Even and Odd Natural Numbers \hspace{1cm}
Even numbers are divisible by 2 without Every other number on the number line |
Odd numbers are not divisible by 2 without Every other number on the number line |
There are four properties of natural numbers.
\bf{1} . Closure Property of Natural Numbers |
|---|
The sum and product of two natural numbers are also natural numbers.
The closure property does not work all the time for subtraction and division.
|
\bf{2} . Associative Property of Natural Numbers |
|---|
The sum and product of three natural numbers are the same even if the numbers (1 + 3) + 5 = 9
(1 \times 3) \times 5 = 15
The associative property does not work all the time for subtraction and division.
|
Step by step guide: Associative Property
\bf{3} . Commutative Property of Natural Numbers |
|---|
The sum and product of two natural numbers is the same even if the order is
The commutative property does not work all the time for subtraction and division.
|
Step-by-step guide: Commutative Property
\bf{4} . Distributive Property of Natural Numbers |
|---|
For three natural numbers, multiplication is distributive over addition and subtraction 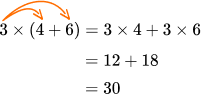 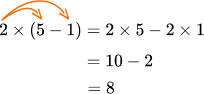 |
Step-by-step guide: Distributive Property
What are natural numbers?
Common Core State Standards
How does this apply to kindergarten through 6th grade?
- Kindergarten – Counting and Cardinality (K.CC.B.4)
Understand the relationship between numbers and quantities; connect counting to cardinality.
- Grade 1 – Operations and Algebraic Thinking (1.0A.B.3 )
Apply properties of operations as strategies to add and subtract.
Examples: If 8 + 3 = 11 is known, then 3 + 8 = 11 is also known. (Commutative property of addition).
To add 2 + 6 + 4, the second two numbers can be added to make a ten, so 2 + 6 + 4 = 2 + 10 = 12. (Associative property of addition.)
- Grade 2 – Operations and Algebraic Thinking (2.OA.C.3)
Determine whether a group of objects (up to 20 ) has an odd or even number of members, e.g., by pairing objects or counting them by 2 s; write an equation to express an even number as a sum of two equal addends.
- Grade 3 – Operations and Algebraic Thinking (3.OA.B.5)
Apply properties of operations as strategies to multiply and divide.
Examples: If 6 \times 4 = 24 is known, then 4 \times 6 = 24 is also known. (Commutative property of multiplication).
3 \times 5 \times 2 can be found by 3 \times 5 = 15, then 15 \times 2 = 30, or by 5 \times 2 = 10, then 3 \times 10 = 30. (Associative property of multiplication).
Knowing that 8 \times 5 = 40 and 8 \times 2 = 16, one can find 8 \times 7 as 8 \times (5 + 2) = (8 \times 5) + (8 \times 2) = 40 + 16 = 56. (Distributive property).
- Grade 4 – Number and Operations Base Ten (4.NBT.B.5)
Multiply a whole number of up to four digits by a one-digit whole number, and multiply two two-digit numbers, using strategies based on place value and the properties of operations. Illustrate and explain the calculation by using equations, rectangular arrays, and/or area models.
- Grade 6 – Number Systems (6.NS.B.4)
Find the greatest common factor of two whole numbers less than or equal to 100 and the least common multiple of two whole numbers less than or equal to 12. Use the distributive property to express a sum of two whole numbers 1–100 with a common factor as a multiple of a sum of two whole numbers with no common factor. For example, express 36 + 8 as 4 \, (9 + 2).
How to use natural numbers
In order to classify natural numbers:
- Recall the definition of the type of number needed.
- Show whether the number fits or does not fit the definition.
In order to apply a property of natural numbers:
- Recall the property.
- Use the property to get an answer.
![[FREE] Types of Number Check for Understanding Quiz (Grade 2, 4 and 6)](https://thirdspacelearning.com/wp-content/uploads/2023/06/Types-of-number-check-for-understanding-listing-image.jpg)
[FREE] Types of Number Check for Understanding Quiz (Grade 2, 4 and 6)
![[FREE] Types of Number Check for Understanding Quiz (Grade 2, 4 and 6)](https://thirdspacelearning.com/wp-content/uploads/2023/06/Types-of-number-check-for-understanding-listing-image.jpg)
Use this quiz to check your grade 6 students’ understanding of types of numbers. 10+ questions with answers covering a range of 2nd, 4th and 6th grade types of numbers topics to identify areas of strength and support!
DOWNLOAD FREE![[FREE] Types of Number Check for Understanding Quiz (Grade 2, 4 and 6)](https://thirdspacelearning.com/wp-content/uploads/2023/06/Types-of-number-check-for-understanding-listing-image.jpg)
[FREE] Types of Number Check for Understanding Quiz (Grade 2, 4 and 6)
![[FREE] Types of Number Check for Understanding Quiz (Grade 2, 4 and 6)](https://thirdspacelearning.com/wp-content/uploads/2023/06/Types-of-number-check-for-understanding-listing-image.jpg)
Use this quiz to check your grade 6 students’ understanding of types of numbers. 10+ questions with answers covering a range of 2nd, 4th and 6th grade types of numbers topics to identify areas of strength and support!
DOWNLOAD FREEIdentifying natural numbers examples
Example 1: identifying natural numbers
Is the number identified on the number line a natural number?

- Recall the definition of the type of number needed.
Natural numbers are whole positive numbers beginning with 1.
2Show whether the number fits or does not fit the definition.
The number identified on the number line is \, \cfrac{2}{5} \, which is a fraction.
So, the number identified on the number line is not a natural number.
Example 2: identifying types of natural numbers
Is 13 an odd natural number?
Recall the definition of the type of number needed.
An odd number is not divisible by 2 without a remainder. Odd numbers end in 1, 3, 5, 7, 9.
Show whether the number fits or does not fit the definition.
13 is not divisible by 2 without a remainder and ends in a 3.
So, 13 is an odd number.
Example 3: identifying types of natural numbers
Is 19 a prime number?
Recall the definition of the type of number needed.
A prime number is a number with exactly two factors: itself and 1.
Show whether the number fits or does not fit the definition.
The factors of 19 are 1 and 19.
So, 19 is a prime number.
Example 4: apply a property of natural numbers
Find the missing number using the associative property of addition.
(5 + 2) + \, \rule{0.5cm}{0.15mm} \, = 5 + (2 + 9)
Recall the property.
The associative property of addition is (a + b) + c = a + (b + c)
Use the property to get an answer.
(5 + 2) + {\color{blue} 9} = 5 + (2 + 9)
9 is the missing number because (5 + 2) + 9 = 5 + (2 + 9) = 16
Example 5: apply a property of natural numbers
Find the missing number using the commutative property of multiplication.
19 \times 12 = 12 \times \, \rule{0.5cm}{0.15mm}
Recall the property.
The commutative property of multiplication is a \times b = b \times c
Use the property to get an answer.
19 \times 12 = 12 \times {\color{blue} 19}
19 is the missing number because 19 \times 12 = 228 and 12 \times 19 = 228
Example 6: properties of natural numbers
Find the missing number in the distributive property equation.
8 \times (5 + 3) = \, \rule{0.5cm}{0.15mm} \, + 24
Recall the property.
The distributive property is a \, (b + c) = ab + ac
Use the property to get an answer.
8 \times (5 + 3) = {\color{blue} 40} + 24
\color{blue} 40 is the missing number.
Teaching tips for natural numbers lessons
- Natural numbers are students’ first experience with numbers because they are the counting numbers. When first teaching the concept of numbers to young mathematicians, associate the actual numeral with the correct number of dots so that students can associate the numeral with a quantity.
- Use a number line so students can visually see a representation of the numbers.
- To build number sense, expose students to number patterns.
- Use a Venn diagram when teaching students in middle school the real number system. Using the diagram will help students visualize how whole numbers, integers, and rational numbers (all the number sets) build upon the natural numbers.
Easy mistakes to make
- Thinking \bf{0} is a natural number
Natural numbers are counting numbers and begin with the number 1.
0 is not part of the natural number set.
- Thinking all integers are natural numbers
Only the non-negative integers are natural numbers not including 0.
- Thinking that natural numbers are not part of integers
Natural numbers are a subset of the integers because they represent the positive integers.
Related types of numbers lessons
This natural numbers topic guide is part of our series on types of numbers. You may find it helpful to start with the main types of numbers topic guide for a summary of what to expect or use the step-by-step guides below for further detail on individual topics. Other topic guides in this series include:
Practice natural numbers
1. Which of the following numbers is a natural number?




Natural numbers are the set of whole positive numbers that start at 1.
15 is a positive whole number so it is a natural number.
2. Which group of numbers are natural numbers?




Natural numbers are the set of whole positive numbers that start at 1.
So, 1, 2, 3 are natural numbers.
3. Which group of numbers represents prime numbers?




A prime number is a number that has exactly two factors, 1 and itself.
2, 3, 7 represent prime numbers because:
The factors of 2 are 1 and 2.
The factors of 3 are 1 and 3.
The factors of 7 are 1 and 7.
4. Find the missing number using the associative property.
(6 + 5) + 10 = 6 + ( \, \rule{0.5cm}{0.15mm} \, + 10)




The associative property is (a + b) + c = a + (b + c).
So, (6 + 5) + 10 = 6 + (5 + 10)
(6 + 5) + 10 = 21
6 + (5 + 10) = 21
5. Find the missing number using the commutative property.
12 \times \, \rule{0.5cm}{0.15mm} \, = 8 \times 12




The commutative property is a \times b = b \times a.
So, 12 \times 8 = 8 \times 12.
12 \times 8 = 96
8 \times 12 = 96
6. Find the missing number using the distributive property.
4 \times (2 + 9) = 8 + \, \rule{0.5cm}{0.15mm}




The distributive property is a \times (b + c) = a \times b + a \times c.
So, 4 \times (2 + 9) = 8 + 36 = 44
Natural numbers FAQs
No, natural numbers are positive whole numbers that start with 1.
No, only positive whole numbers are natural numbers. Positive fractions and decimals are not natural numbers.
No, only the non-negative integers starting with 1 are natural numbers.
Cardinal numbers are natural numbers used for counting. They are countable numbers.
Ordinal numbers are natural numbers used for ordering objects such as 1 st, 2 nd, 3 rd, etc…
Only the positive integers are rational numbers, not including 0. Negative numbers are not natural numbers, and fractions and decimals are not natural numbers. Natural numbers are a subset of rational numbers.
Set theory serves as a foundation for everything that is done in mathematics because it builds concepts of numbers.
The next lessons are
Still stuck?
At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.
Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.

Find out how we can help your students achieve success with our math tutoring programs.
[FREE] Common Core Practice Tests (3rd to 8th Grade)
Prepare for math tests in your state with these 3rd Grade to 8th Grade practice assessments for Common Core and state equivalents.
Get your 6 multiple choice practice tests with detailed answers to support test prep, created by US math teachers for US math teachers!