[FREE] Fun Math Games & Activities Packs
Always on the lookout for fun math games and activities in the classroom? Try our ready-to-go printable packs for students to complete independently or with a partner!
Odd numbers
Here you will learn about odd numbers, including examples of odd numbers, odd numbers on a number line and a number chart, and properties of odd numbers.
Students will first learn about odd numbers as part of operations and algebraic thinking in 2nd grade. They expand upon their knowledge of odd numbers in 3rd grade when they identify arithmetic patterns and properties of numbers.
What are odd numbers?
Odd numbers are whole numbers that are not divisible by 2 without remainders.
The last digit of an odd number is 1, 3, 5, 7, or 9.
Odd numbers are the opposite of even numbers, which are divisible by 2. An even number’s last digit is 0, 2, 4, 6, or 8.
For example


To identify an odd number, you can look at the last digit, use a number line, or use a number chart.
Last digit
| The last digit of a number, or the digit in the ones place, will tell 2,631,903,42\underline{3}
|
Number line
| Start with a number whose last digit is 1, 3, 5, 7, or 9 and jump 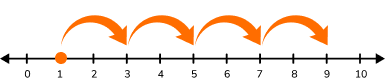 |
Number chart
| On a number chart each column that begins with 1, 3, 5, 7, or 9 This chart shows a list of odd numbers between 1 and 100. 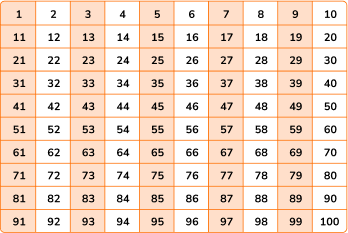 |
Properties of even numbers and odd numbers
- Property of addition
- If you add an even number to an even number, the sum will always be an even number. For example, 8 + 4 = 12 .
- If you add an even number to an odd number, the sum will always be an odd number. For example, 8 + 3 = 11 .
- If you add an odd number to an odd number, the sum will always be an even number. For example, 5 + 3 = 8 .
- Property of subtraction
- If you subtract an even number from an even number, the difference will always be an even number. For example, 16-10 = 6 .
- If you subtract an even number from an odd number or an odd number from an even number, the difference will always be an odd number. For example, 16-9 = 7; 17-10 = 7 .
- If you subtract an odd number from an odd number, the difference will always be an even number. For example, 9-5 = 4 .
- Property of multiplication
- If you multiply an even number by an even number, the product will always be an even number. For example, 4 \times 2 = 8.
- If you multiply an even number by an odd number, the product will always be an even number. For example, 4 \times 5 = 20 .
- If you multiply an odd number by an odd number, the product will always be an odd number. For example, 3 \times 5 = 15 .
Groups of objects
- To determine if a group of objects has an even number of objects or an odd number of objects, group the objects into pairs, or equal groups of 2. If each object can be grouped into a pair, there is an even number of objects. If there is one object left over after pairing, there is an odd number of objects.
For example,
Since all of the objects in this group can be  | After grouping the objects into pairs, there is  |
What are odd numbers?

Common Core State Standards
How does this relate to 2nd grade math?
- Grade 2 – Operations and Algebraic Thinking (2.OA.3)
Determine whether a group of objects (up to 20 ) has an odd or even number of members, for example, by pairing objects or counting them by 2 s; write an equation to express an even number as a sum of two equal addends.
How to identify odd numbers
In order to identify odd numbers:
- Look at the last digit, or the digit in the ones place. If the digit is \bf{1, 3, 5, 7,} or \bf{9,} the number is odd.
- Use this strategy to answer the question.
In order to determine if the answer to an equation will be an odd number:
- Recall the properties of addition, subtraction, or multiplication for odd numbers.
- Apply the correct property.
In order to determine if there is an odd number of objects in a group:
- Group the objects into pairs.
- If all objects can be grouped into pairs, there is an even number of objects. If there is one left over, there is an odd number of objects.
![[FREE] Types of Number Check for Understanding Quiz (Grade 2, 4 and 6)](https://thirdspacelearning.com/wp-content/uploads/2023/06/Types-of-number-check-for-understanding-listing-image.jpg)
[FREE] Types of Number Check for Understanding Quiz (Grade 2, 4 and 6)
![[FREE] Types of Number Check for Understanding Quiz (Grade 2, 4 and 6)](https://thirdspacelearning.com/wp-content/uploads/2023/06/Types-of-number-check-for-understanding-listing-image.jpg)
Use this quiz to check your grade 6 students’ understanding of types of numbers. 10+ questions with answers covering a range of 2nd, 4th and 6th grade types of numbers topics to identify areas of strength and support!
DOWNLOAD FREE![[FREE] Types of Number Check for Understanding Quiz (Grade 2, 4 and 6)](https://thirdspacelearning.com/wp-content/uploads/2023/06/Types-of-number-check-for-understanding-listing-image.jpg)
[FREE] Types of Number Check for Understanding Quiz (Grade 2, 4 and 6)
![[FREE] Types of Number Check for Understanding Quiz (Grade 2, 4 and 6)](https://thirdspacelearning.com/wp-content/uploads/2023/06/Types-of-number-check-for-understanding-listing-image.jpg)
Use this quiz to check your grade 6 students’ understanding of types of numbers. 10+ questions with answers covering a range of 2nd, 4th and 6th grade types of numbers topics to identify areas of strength and support!
DOWNLOAD FREEOdd numbers examples
Example 1: identifying odd numbers
True or false: 823 is an odd number.
- Look at the last digit, or the digit in the ones place. If the digit is \bf{1, 3, 5, 7,} or \bf{9,} the number is odd.
The last digit, or the digit in the ones place, is 3.
2Use this strategy to answer the question.
Since the last digit in 823 is 3, it is an odd number, so the statement is true.
Example 2: identifying odd numbers
List all consecutive odd numbers between 61 and 71.
Look at the last digit, or the digit in the ones place. If the digit is \bf{1, 3, 5, 7,} or \bf{9,} the number is odd.
All numbers between 61 and 71 are:
61, 62, 63, 64, 65, 66, 67, 68, 69, 70, 71
Find the numbers that end in 1, 3, 5, 7, or 9 :
6\underline{1}, 62, 6\underline{3}, 64, 6\underline{5}, 66, 6\underline{7}, 68, 6\underline{9}, 70, 7\underline{1}
Use this strategy to answer the question.
The odd numbers between 61 and 71 are 61, 63, 65, 67, 69, 71 .
Example 3: identifying odd numbers
Look at the list of numbers. Which numbers are odd?
17, 438, 282, 500, 901, 744, 355, 483, 809, 620
Look at the last digit, or the digit in the ones place. If the digit is \bf{1, 3, 5, 7,} or \bf{9,} the number is odd.
1\underline{7}, 43\underline{8}, 28\underline{2}, 50\underline{0}, 90\underline{1}, 74\underline{4}, 35\underline{5}, 48\underline{3}, 80\underline{9}, 62\underline{0}

Use this strategy to answer the question.
The odd numbers are 17, 901, 355, 483, and 809 .
Example 4: apply properties of odd numbers
Joe is subtracting an odd number from an odd number. He thinks the difference will be an odd number, but his friend Samira says it will be even. Who is correct?
Recall the properties of addition, subtraction, or multiplication for odd numbers.
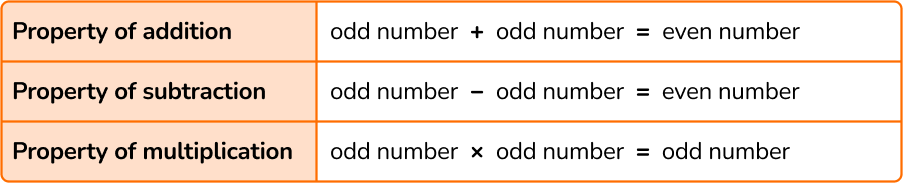
Apply the correct property.
Since Joe is subtracting, he will use the property of subtraction which says an odd number subtracted from an odd number will always result in an even number. Therefore, Samira is correct.
Example 5: apply properties of odd numbers
Anna solves the following equation:
105,915 + 27,863 = 133,775
Her friend glances at the equation and tells her it’s incorrect. How does her friend know this is incorrect?
Recall the properties of addition, subtraction, or multiplication for even numbers.
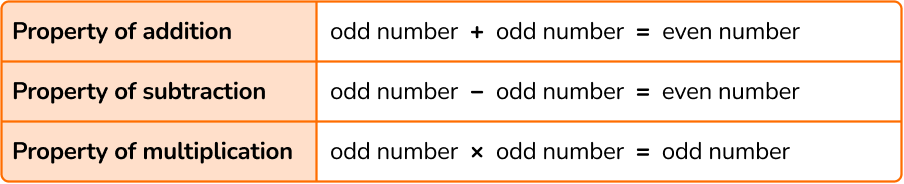
Apply the correct property.
The two numbers being added together end in a 5 and a 3, respectively. That means they are both odd numbers.
105,91\underline{5} + 27,86\underline{3} = 133,77\underline{5}
The property of addition of odd numbers says an odd number plus an odd number will always result in an even number.
The last digit of Anna’s answer is a 5, which means it is an odd number, so Anna’s answer can’t be correct.
Example 6: determine if a group of objects is odd
Look at the objects in the square. Is there an odd number of objects?

Group the objects into pairs.
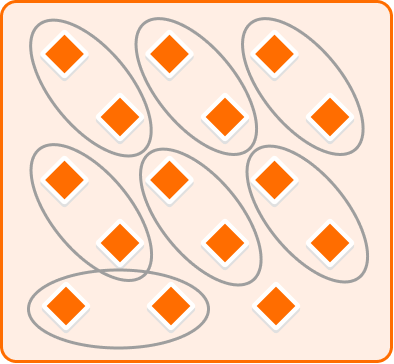
If all objects can be grouped into pairs, there is an even number of objects. If there is one left over, there is an odd number of objects.
All of the objects have been grouped into pairs, but there is one left over. Therefore, there is an odd number of objects.
(The total number of objects is 15 .)
Teaching tips for odd numbers
- Hang a number chart, or hundreds chart, in your classroom with odd numbers highlighted.
- Provide worksheets with practice questions that require students to find odd numbers between any given numbers. For example, instead of always starting at 0, give them a starting number of 63 and ask them to find the odd numbers through 100.
- Provide worksheets with practice questions that ask students to find the next odd numbers and find consecutive odd numbers to build on their understanding of odd numbers. Allow students to use a number line if needed.
Easy mistakes to make
- Thinking you can’t count by \bf{2} s using odd numbers
Students may think that you can only count by 2 s using even numbers since odd numbers are not multiples of 2. However, if you start at an odd digit and count by 2 s, each number will be odd.
- Thinking that fractions and decimals can be odd numbers
Only integers (whole numbers and their corresponding negative numbers) can be odd numbers. Students may think that a number such as 2.43 is an odd number because its last digit is a 3. However, this is not the case as fractions and decimals can not be even numbers or odd numbers.
Related types of numbers lessons
Practice odd numbers questions
1. Which of the following is an odd number?




The last digit of an odd number is 1, 3, 5, 7, or 9.
Therefore, 21 is an odd number.
2. What is the smallest odd number?




One is the smallest odd number because it is the smallest positive whole number that is not divisible by 2.
3. What are the odd numbers between 195 and 204?




The last digit of an odd number is always 1, 3, 5, 7, or 9.
195, 197, 199, 201, and 203 are the only set of numbers that all end in one of those digits.
4. When you add an odd number and an odd number, the answer will…
always be an even number.

sometimes be an even number.

never be an even number.

always be an odd number

The property of addition of odd numbers says that when you add an odd number to an odd number, the sum will always be an even number.
5. True or false: When you subtract an odd number from an odd number, you will get an odd number.
True because the property of subtraction of odd numbers says \text{odd number } – \text{ odd number } = \text{ odd number}

False because the property of subtraction of odd numbers says \text{odd number } – \text{ odd number } = \text{ even number}

True because the property of subtraction of odd numbers says \text{odd number } – \text{ odd number } = \text{ even number}

False because the property of subtraction of odd numbers says \text{odd number } – \text{ odd number } = \text{ odd number}

The property of subtraction of odd numbers says when you subtract an odd number from an odd number, the difference will always be an even number.
6. Look at the group of shapes inside the circle. Is there an odd number of shapes?

Yes because if you group the shapes into pairs, there is one left over.

No because if you group the shapes into pairs, there is one left over.

No because if you group the shapes into pairs, there are none left over.

Yes because if you group the shapes into pairs, there are none left over.

If you group the shapes into pairs, you will see there are none left over.
This means there is an even number of shapes. (The total number of shapes is 14. )
Odd numbers FAQs
An odd number is a whole number that is not a multiple of 2. This means that odd numbers are not divisible by 2 with no remainders.
An even number is divisible by 2 with no remainders and an odd number is not. The last digit of an even number is 0, 2, 4, 6, or 8, while the last digit of an odd number is 1, 3, 5, 7, or 9.
Even numbers and odd numbers are all positive integers and negative integers. Therefore, fractions and decimals are neither even nor odd.
The next lessons are
Still stuck?
At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.
Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.

Find out how we can help your students achieve success with our math tutoring programs.
[FREE] Common Core Practice Tests (Grades 3 to 6)
Prepare for math tests in your state with these Grade 3 to Grade 6 practice assessments for Common Core and state equivalents.
40 multiple choice questions and detailed answers to support test prep, created by US math experts covering a range of topics!
