[FREE] Fun Math Games & Activities Packs

Always on the lookout for fun math games and activities in the classroom? Try our ready-to-go printable packs for students to complete independently or with a partner!

DOWNLOAD FREE

In order to access this I need to be confident with:

Addition and subtraction Skip counting Multiplication and division

Math resources Number and quantity Types of numbers

Composite number

Prime and composite numbers

Here you will learn about prime and composite numbers, including what prime and composite numbers are and how to determine whether a number is prime or composite.

Students will first learn about prime and composite numbers as a part of operations and algebraic thinking in $4$ th grade.

What are prime and composite numbers?

Prime numbers are natural numbers (whole numbers) that are greater than $1$ and cannot be divided by any other whole number other than itself and $1.$

The number $1$ is not a prime number since it only has one factor, $1.$

For example, the number $7$ is prime because it has $2$ divisors, $1$ and itself, $7.$

Composite numbers are positive integers that have more than two factors.

For example, the number $12$ is composite because it has $6$ divisors, $1, 2, 3, 4, 6,$ and $12.$

There are two types of composite numbers, even composite numbers and odd composite numbers. To determine whether a number is composite, you can use the following properties of composite numbers:

A composite number has more than two factors.
The smallest composite number is $4.$
All even numbers are composite, except for the number $2.$
The number has at least two prime factors.

Identifying prime and composite numbers

To determine if a number is a prime number or composite number, you can use the divisibility test to find the factors of a number. If the given number has only $2$ factors $(1$ and itself $)$ the number is prime. If the given number has more than $2$ factors, it’s composite.

To perform a divisibility test, you can use the following divisibility rules:

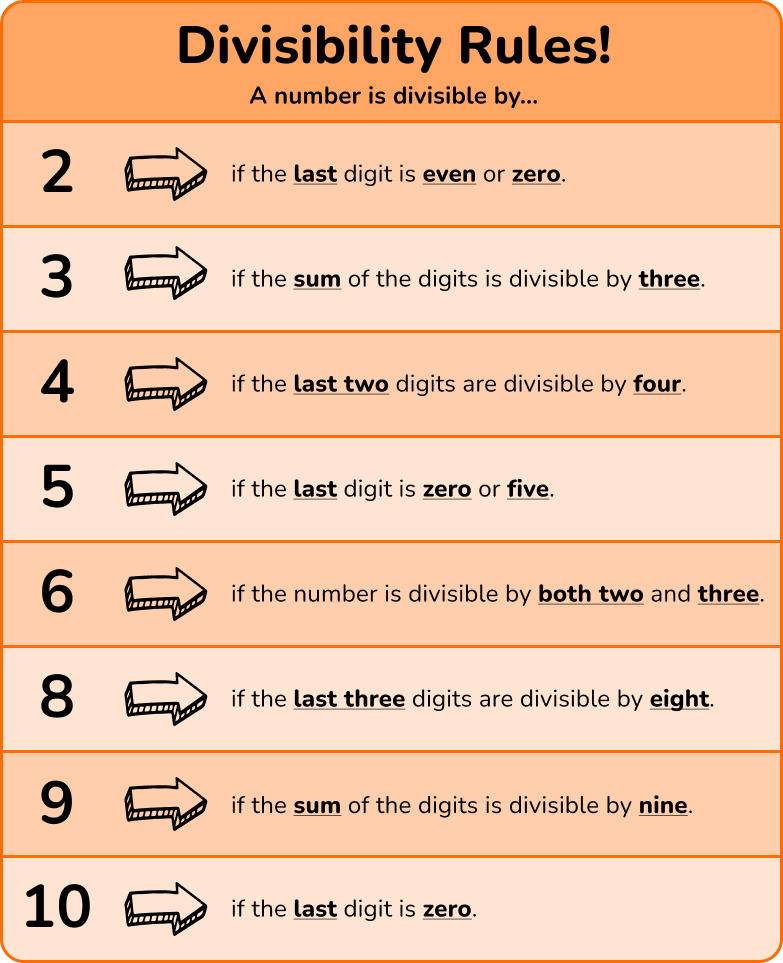
What are prime and composite numbers?

Common Core State Standards

How does this relate to $4$ th grade math?

Grade 4: Operations and Algebraic Thinking (4.OA.B.4)
Find all factor pairs for a whole number in the range $1-100.$ Recognize that a whole number is a multiple of each of its factors. Determine whether a given whole number in the range $1-100$ is a multiple of a given one-digit number. Determine whether a given whole number in the range $1-100$ is prime or composite.

[FREE] Types of Number Check for Understanding Quiz (Grade 2, 4 and 6)

Use this quiz to check your grade 6 students’ understanding of types of numbers. 10+ questions with answers covering a range of 2nd, 4th and 6th grade types of numbers topics to identify areas of strength and support!

DOWNLOAD FREE

[FREE] Types of Number Check for Understanding Quiz (Grade 2, 4 and 6)

DOWNLOAD FREE

How to identify prime and composite numbers

In order to determine whether a number is a prime number or composite number:

Use the divisibility rules to see whether $\bf{2, 3}$ or $\bf{5}$ is a factor.
If they are not factors, test for divisibility by $\bf{7}$ and $\bf{8}.$
State whether the number is prime or composite.

Prime and composite numbers examples

Example 1: determine if a given number is prime or composite

Is $17$ prime or composite?

Use the divisibility rules to see whether $\bf{2, 3}$ or $\bf{5}$ is a factor.

The last digit is not a $2, 4, 6, 8,$ or $0$ so it is not a multiple of $2.$

Adding the digits together, we have $1+7=8,$ so it is not a multiple of $3.$

The last digit is not a $5$ or a $0,$ and so it is not a multiple of $5.$

2If they are not factors, test for divisibility by $\bf{7}$ and $\bf{8}.$

Start by dividing by $7\text{:}$

As $17 \div 7=2 \; r 3, \, 7$ is not a factor of $17.$

Next divide by $8\text{:}$

As $17 \div 8=2 \; r 1, \, 8$ is not a factor of $17.$

The number $17$ is not divisible by $7$ or $8,$ so there are no more whole numbers that you need to try.

3State whether the number is prime or composite.

$17$ is a prime number as it only has two factors, $1$ and $17.$

Example 2: determine if a given number is prime or composite

Is $63$ prime or composite?

Use the divisibility rules to see whether $\bf{2, 3}$ or $\bf{5}$ is a factor.

The last digit is not a $2, 4, 6, 8,$ or $0,$ so it is not a multiple of $2.$

Adding the digits together you have $6+3=9$ , so it is a multiple of $3.$

The number $63$ is divisible by $3,$ so there are no more whole numbers that we need to try.

If they are not factors, test for divisibility by $\bf{7}$ and $\bf{8}.$

The number $63$ is divisible by $3,$ so there are no more whole numbers that you need to try.

State whether the number is prime or composite.

$63$ is a composite number.

Example 3: determine if the given numbers are prime numbers or composite numbers.

Use the divisibility rules to see whether $\bf{2, 3}$ or $\bf{5}$ is a factor.

The last digit of $16$ is a $6,$ so $16$ is a multiple of $2.$

If you add the digits of $27$ together, you get $2+7=9,$ which is a multiple of $3.$ $27$ is a multiple of $3.$

The number $5$ has a $5$ as a factor, but it’s the only factor other than $1.$ $5$ is prime.

The last digit of $92$ is $2,$ so $92$ is also a multiple of $2.$

If they are not factors, test for divisibility by $\bf{7}$ and $\bf{8}.$

Divide $77$ by $7$ and $8$ until you reach the first number that gives a quotient that is a whole number.

Start by dividing by $7\text{:}$

$77 \div 7=11,$ which is a factor of $7.$

State whether the number is prime or composite.

The numbers $16, 27, 77$ and $92$ are composite and the number $5$ is prime.

Example 4: determine if the given numbers are prime numbers or composite numbers.

Use the divisibility rules to see whether $\bf{2, 3}$ or $\bf{5}$ is a factor.

The last digit of $24$ and $54$ are even, so both numbers have a factor of $2.$

The number $5$ ends in a $0$ or $5,$ so it has a factor of $5.$

If they are not factors, test for divisibility by $\bf{7}$ and $\bf{8}.$

Divide $17$ and $89$ by $7$ and $8,$ using long division, until you reach the first number that gives a quotient that is a whole number.

Start by dividing $17$ by $7\text{:}$

As $17 \div 7=2 \; r 3, \, 7$ is not a factor of $17.$

Next, divide $17$ by $8\text{:}$

As $17 \div 8=2 \; r 1, \, 7$ is not a factor of $17.$

Next, divide $89$ by $7\text{:}$

As $89 \div 7=12 \; r 5, \, 7$ is not a factor of $89.$

Next, divide $89$ by $8\text{:}$

As $89 \div 8=11 \; r 1, \, 8$ is not a factor of $89.$

The numbers $17$ and $89$ are not divisible by $7$ or $8,$ so there are no more whole numbers that need to be tried.

State whether the number is prime or composite.

The numbers $24, 35$ and $54$ are composite, and the numbers $17$ and $89$ are prime.

Example 5: list the composite numbers between 90 and 99.

Use the divisibility rules to see whether $\bf{2, 3}$ or $\bf{5}$ is a factor.

Determine which of the following numbers are composite:

$91, 92, 93, 94, 95, 96, 97,$ and $98.$

$92, 94, 96$ and $98$ end with even numbers, meaning that $2$ is a factor.

$93$ has $3$ as a factor because when you add the digits, $9+3=12, 12$ is divisible by $3.$

$95$ ends in a $5$ or $0,$ so $5$ is a factor of $95.$

If they are not factors, test for divisibility by $\bf{7}$ and $\bf{8}.$

Divide $91$ and $97$ by $7$ and $8,$ using long division, until you reach the first number that gives a quotient that is a whole number.

Start by dividing $91$ by $7\text{:}$

As $91 \div 7=13, \, 7$ is a factor of $97.$

Next, divide $97$ by $7\text{:}$

As $97 \div 7=13 \; r 6, \, 7$ is not a factor of $97.$

Next, divide $97$ by $8\text{:}$

As $97 \div 8=12 \; r 1, \, 8$ is not a factor of $97.$

The number $97$ is not divisible by $7$ or $8,$ so there are no more whole numbers that need to be tried.

State whether the number is prime or composite.

The composite numbers between $90$ and $99$ are: $91, 92, 93, 94, 95, 96$ and $98.$

Example 6: list the prime numbers between 60 and 70.

Use the divisibility rules to see whether $\bf{2, 3}$ or $\bf{5}$ is a factor.

Determine which of the following numbers are prime:

$61, 62, 63, 64, 65, 66, 67, 68, 69.$

$62, 64, 66$ and $68$ end with even numbers, meaning that $2$ is a factor.

$63$ has $3$ as a factor because when you add the digits, $6+3=9, 9$ is divisible by $3.$

$65$ ends in a $5$ or $0,$ so $5$ is a factor of $65.$

$69$ has $3$ as a factor because when you add the digits, $6+9=15, 15$ is divisible by $3.$

If they are not factors, test for divisibility by $\bf{7}$ and $\bf{8}.$

Divide $61$ and $67$ by $7$ and $8,$ using long division, until you reach the first number that gives a quotient that is a whole number.

Start by dividing $61$ by $7\text{:}$

As $61 \div 7=8 \; r 5, \, 7$ is not a factor of $61.$

Next, divide $61$ by $8\text{:}$

As $61 \div 8=7 \; r 5, \, 8$ is not a factor of $61.$

Next, divide $67$ by $7\text{:}$

As $67 \div 7=9 \; r 4, \, 7$ is not a factor of $67.$

Next, divide $67$ by $8\text{:}$

As $67 \div 8=8 \; r 3, \, 8$ is not a factor of $67.$

The numbers $61$ and $67$ are not divisible by $7$ or $8,$ so there are no more whole numbers that need to be tried.

State whether the number is prime or composite.

The prime numbers between $60$ and $70$ are $61$ and $67.$

Teaching tips for prime and composite numbers

Have students in your math classes find examples of composite numbers using divisibility rules to compile in a class list. This list can be printed and given as a list of composite numbers and a list of prime numbers to refer back to when needed.

Instead of using worksheets where students have to identify whether a number is prime or composite, use manipulative and hands-on activities for students to sort numbers.

Easy mistakes to make

$\bf{1}$ is not a prime or composite number
$1$ is not a prime or composite number. This is because it only has one factor, rather than the $2$ or more factors needed to be prime or composite.

All even numbers are composite
$2$ is the only even prime number, because it only has two factors, $1$ and itself. Every other even number is divisible by $2. \, 2$ is a special case when discussing prime numbers.

All prime numbers are odd
All but one of the prime numbers are odd, it can be assumed that all odd numbers are prime. However, not all odd numbers are prime, and not all prime numbers are odd. For example, the number $15$ is an odd number. The number $15$ is a multiple of $3$ and $5$ and is composite.

Practice prime and composite numbers questions

Neither

Not enough information is given

Prime

Composite

Use divisibility rules to determine whether $49$ is prime or composite.

$49$ is not a multiple of $2, 3$ or $5,$ so test divisibility for $7$ or $8.$

$49 \div 7=7,$ so $7$ is a factor of $49.$

$49$ is composite.

Prime

Composite

Neither

Not enough information is given

Use divisibility rules to determine whether $73$ is prime or composite.

$73$ is not a multiple of $2, 3$ or $5,$ so test divisibility for $7$ or $8.$

$73 \div 7=10 \; r3,$ so $7$ is not a factor of $73.$

$73 \div 8=9 \; r1,$ so $8$ is not a factor of $73.$

$73$ is prime.

54

82

87

97

Use divisibility rules to determine which number is prime. Prime numbers will only have $2$ factors, $1$ and itself.

$54$ and $82$ are not prime because the last digits of the numbers are even, meaning $2$ is a factor.

$87$ is not prime because when you add the digits, $8+7=15, \, 15$ is divisible by $3,$ making $3$ a factor of $87.$

$97$ is prime.

23

33

59

83

Use divisibility rules to determine which number is composite. Composite numbers have more than $2$ factors.

$33$ is not prime, because when you add the digits, $3+3=6, 6$ is divisible by $3,$ making $3$ a factor of $33.$

$23, 59,$ and $83$ only have $2$ factors, $1$ and itself.

$33$ is composite.

21, 22, 24, 25, 26, 27, 28

21, 22, 23, 25, 26, 27, 28

21, 22, 24, 25, 26, 27, 29

21, 22, 24, 26, 27, 28

Determine which of the following numbers are composite:

21, 22, 23, 24, 25, 26, 27, 28, 29.

$22, 24, 26$ and $28$ end with even numbers, meaning that $2$ is a factor.

$21$ has $3$ as a factor because when you add the digits, $2+1=3, \, 3$ is divisible by $3.$

$25$ ends in a $5$ or $0,$ so $5$ is a factor of $25.$

$27$ has $3$ as a factor because when you add the digits, $2+7=9, \, 9$ is divisible by $3.$

Divide $23$ and $29$ by $7$ and $8,$ using long division, until you reach the first number that gives a quotient that is a whole number.

The numbers $23$ and $29$ are not divisible by $7$ or $8,$ so there are no more whole numbers that need to be tried.

The numbers $21, 22, 24, 25, 26, 27, 28$ are composite numbers.

$73$ and $79$

$72, 74,$ and $78$

$71, 73$ and $79$

71, 73, 75

Determine which of the following numbers are composite:

71, 72, 73, 74, 75, 76, 77, 78, 79.

$72, 74, 76$ and $78$ end with even numbers, meaning that $2$ is a factor.

$75$ ends in a $5$ or $0,$ so $5$ is a factor of $75.$

$77$ has $7$ as a factor because $7 \times 11=77.$

Divide $71, 73$ and $79$ by $7$ and $8,$ using long division, until you reach the first number that gives a quotient that is a whole number.

The numbers $71, 73$ and $79$ are not divisible by $7$ or $8,$ so there are no more whole numbers that need to be tried.

The numbers $71, 73$ and $79$ are prime numbers.

Prime and composite numbers FAQs

What is a primality test?

A primality test is a mathematical algorithm or procedure designed to determine whether a given number is a prime number or not. The goal of such a test is to identify prime numbers without having to factorize the number completely.

What is a highly composite number?

A highly composite number is a positive integer that has more divisors than any positive integer smaller than itself. Examples of highly composite numbers include $2, 4, 6, 12, 24, 48, 60, 120$ and $180.$

The next lessons are

Still stuck?

At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.

Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.