Types Of Numbers - Math Steps, Examples & Questions

High Impact Tutoring Built By Math Experts

Personalized standards-aligned one-on-one math tutoring for schools and districts

Request a demo

In order to access this I need to be confident with:

Reciprocal math

Square numbers

Repeating decimals

Cube numbers

Math resources Number and quantity

Types of numbers

Here you will learn about different types of numbers and how they are related and classified.

Students begin to learn about types of numbers beginning in kindergarten and develop that knowledge from elementary school through high school.

What are types of numbers?

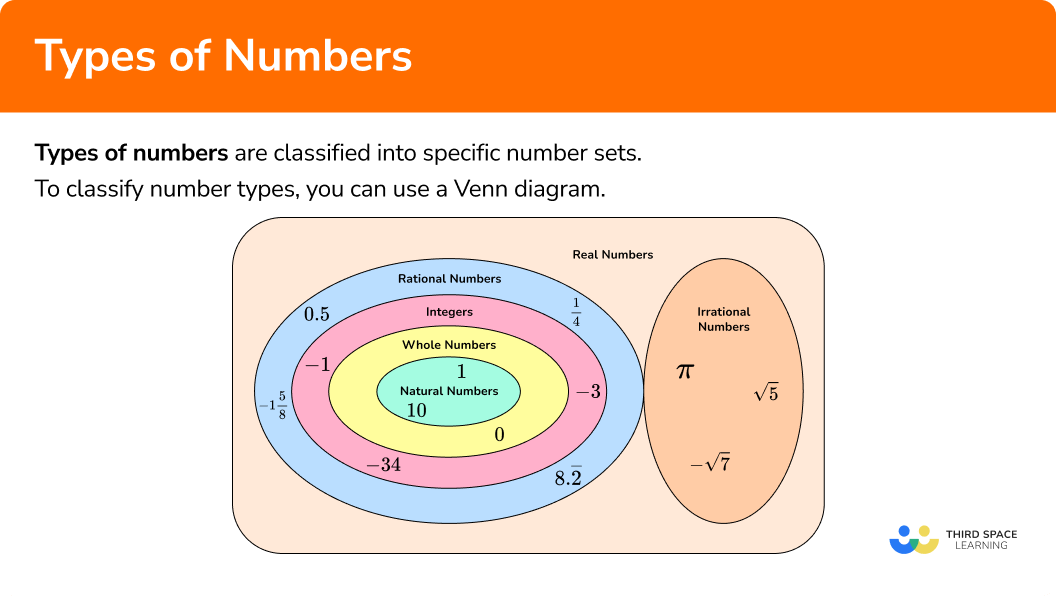
Types of numbers are classified into specific number sets. In elementary school, you will work with the set of rational numbers.

Let’s look at the different types of numbers and how they are classified.

Number Sets	Description	Samples
Natural Numbers	Positive whole numbers also known as the counting numbers.	$1, 2, 3, 4, 5, 6, ...$
Whole Numbers	Positive whole number plus $0.$	$0, 1, 2, 3, 4, 5, 6 ...$
Integers	Positive and negative whole numbers, plus $0.$	$\dots-3, -2, -2, 0, 1, 2, 3...$
Rational Numbers	Any number that can be expressed as a fraction where the numerator and denominator are integers. This includes positive and negative whole numbers, terminating decimals, and repeating decimals.	$-5, 0, 1, \cfrac{4}{5} \, , 1\cfrac{3}{4} \, , -1.\overline{2}, 9.5, 0.\overline{3}$
Irrational Numbers	A number that cannot be expressed as a fraction. This includes positive and negative non-repeating, non-terminating decimals.	$\sqrt{5}, -\sqrt{11}, \sqrt{2}, \pi$
Real Numbers	All of the rational numbers plus the irrational numbers.	$1, \cfrac{4}{5} \, , \sqrt{12}, 0.\overline{53}, 0.\overline{12}, -7, 0, 34$

Step-by-step guide: Natural numbers

Step-by-step guide: Whole numbers

Step-by-step guide: Integers

Step-by-step guide: Rational numbers

Step-by-step guide: Irrational numbers

A Venn diagram can also help you see the number sets.

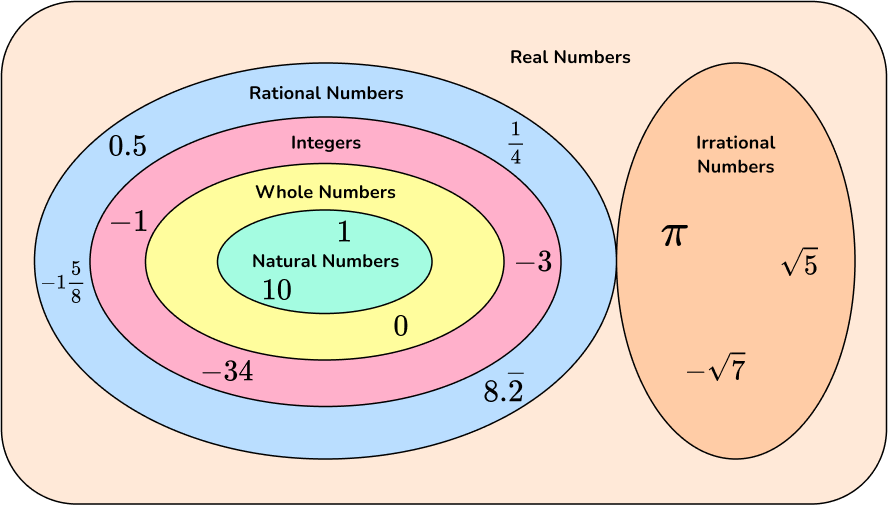
Step-by-step guide: Number sets

Special classifications

Prime and composite numbers


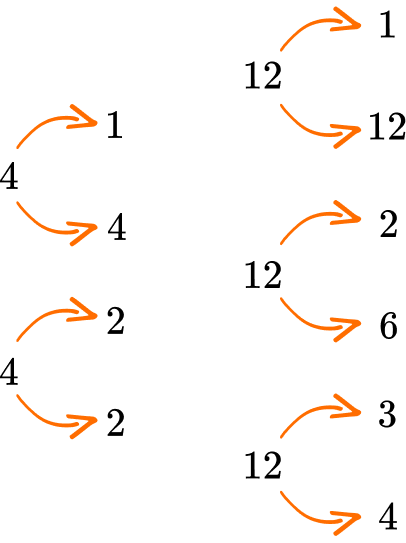
A prime number is a number with exactly two factors: itself and $1.$ $2$ and $7$ are examples of prime numbers. $2$ has $2$ factors: $7$ has $2$ factors: $1, 2 \hspace{2.5cm} 1, 7$ $1 \times 2 = 2 \hspace{2cm} 1 \times 7 = 7$	A composite number is a number with more than two factors. $4$ and $12$ are examples of composite numbers $4$ has $3$ factors: $12$ has $6$ factors: $\hspace{.4cm}1, 2, 4 \hspace{1.9cm} 1, 2, 3, 4, 6, 12$ $\hspace{.2cm}1 \times 4 = 4 \hspace{1.7cm} 1 \times 12 = 12$ $2 \times 2 = 4 \hspace{1.7cm} 2 \times 6 = 12$ $\hspace{3cm} 3 \times 4 = 12$

Step-by-step guide: Prime and composite numbers

Even and Odd Numbers


Even numbers are divisible by $2$ without remainders; they end in $0, 2, 4, 6,$ or $8.$	Odd numbers are not divisible by $2$ without remainders and end in $1, 3, 5, 7,$ or $9.$

Step-by-step guide: Even numbers

Step-by-step guide: Odd numbers

Positive and negative numbers


Positive numbers are numbers that are greater than $0.$ On the number line, they are to the right of $0.$ Positive numbers can be whole numbers, fractions, or decimals.
Negative numbers are numbers that are less than $0.$ On the number line, they are to the left of $0.$ Negative numbers can be whole numbers, fractions, or decimals.

[FREE] Types of Number Worksheet (Grade 2, 4 and 6)

Use this quiz to check your grade 2, 4 and 6 students’ understanding of types of numbers. 10+ questions with answers covering 2nd, 4th, and 6th grade topics to identify learning gaps.

DOWNLOAD FREE

[FREE] Types of Number Worksheet (Grade 2, 4 and 6)

Use this quiz to check your grade 2, 4 and 6 students’ understanding of types of numbers. 10+ questions with answers covering 2nd, 4th, and 6th grade topics to identify learning gaps.

DOWNLOAD FREE

Fractions


Fractions are numbers that are equal parts of a whole. They have a numerator and a denominator separated by a fraction bar. 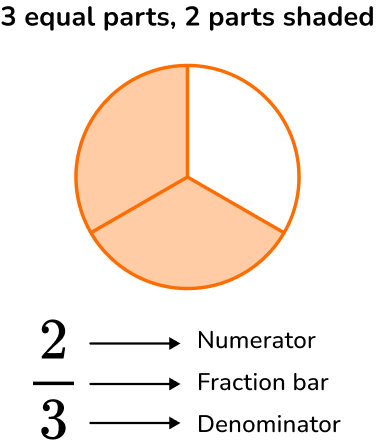Fractions can also be interpreted as division. Numerator → dividend Denominator → divisor Fraction bar → division bar Types of fractions: Proper fractions are fractions where the numerator is less than the denominator. For example, $\, \cfrac{2}{3} \,$ is a proper fraction. Improper fractions are fractions where the numerator is greater than the denominator. For example, $\, \cfrac{4}{3} \,$ is an improper fraction. Mixed numbers (mixed fractions) are an integer with a proper fraction. For example, $\, 1\cfrac{1}{3} \,$ is mixed number.

Fractions are numbers that are equal parts of a whole. They have a numerator and a denominator separated by a fraction bar.

Fractions can also be interpreted as division.

Numerator → dividend

Denominator → divisor

Fraction bar → division bar

Types of fractions:

Proper fractions are fractions where the numerator is less than the denominator.
For example,

\, \cfrac{2}{3} \,

is a proper fraction.

Improper fractions are fractions where the numerator is greater than the denominator.
For example,

\, \cfrac{4}{3} \,

is an improper fraction.

Mixed numbers (mixed fractions) are an integer with a proper fraction.
For example,

\, 1\cfrac{1}{3} \,

is mixed number.

Decimals


Decimals are numbers that are similar to fractions. They have a whole part and a fractional part that are separated by a decimal point. Our decimal system splits whole numbers into tenths, hundredths, thousandths, and so on. For example, $1.21$ is a number in decimal form. It can be represented on a place value chart. 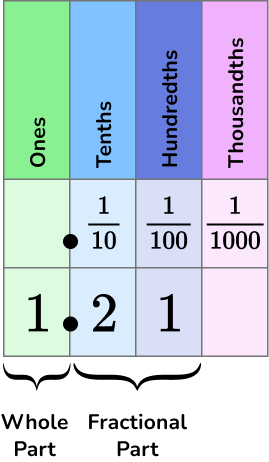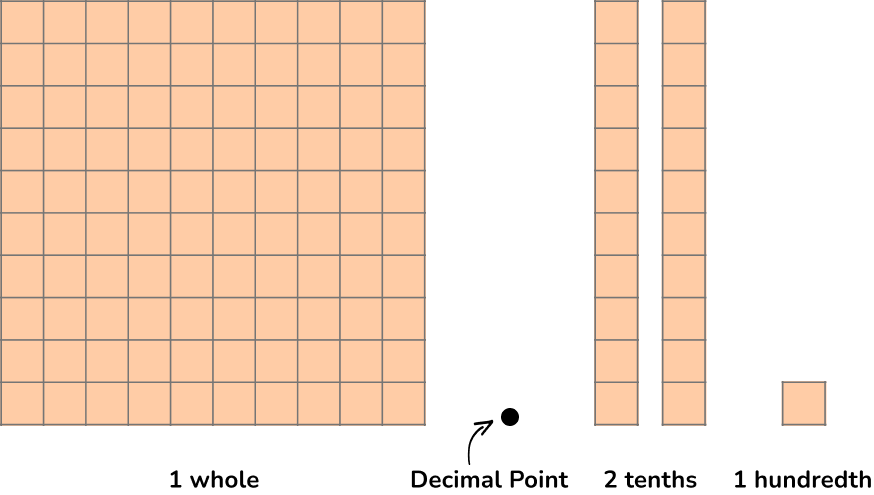$1.21$ can also be represented with place value blocks. Types of Decimals Terminating decimals are decimal numbers with a finite number of decimal places, $1.21$ is a terminating decimal. Terminating decimals can be represented as a fraction. $1.21$ is the same as $1\cfrac{21}{100} = \cfrac{121}{100}$ Repeating decimals are decimal numbers where the a decimal place repeats indefinitely, $0.33333\dots$ or $0.\overline{3}$ is a repeating decimal. The bar above the digit $3$ means that $3$ is repeating. Repeating decimals can be represented as a fraction. $0.\overline{3}$ is the same as $\cfrac{1}{3}$ Non-repeating, non-terminating decimals are decimal numbers that cannot be represented as a fraction. $\pi ,$ (pi) is a non-repeating, non-terminating decimal. $\sqrt{5}$ ( square root of $5$ ) is a non-repeating, non-terminating decimal.

Decimals are numbers that are similar to fractions. They have a whole part and a fractional part that are separated by a decimal point.

Our decimal system splits whole numbers into tenths, hundredths, thousandths, and so on.

For example,

1.21

is a number in decimal form. It can be represented on a place value chart.

1.21

can also be represented with place value blocks.

Types of Decimals

Terminating decimals are decimal numbers with a finite number of decimal places,

1.21

is a terminating decimal. Terminating decimals can be represented as a fraction.

1.21

is the same as

1\cfrac{21}{100} = \cfrac{121}{100}

Repeating decimals are decimal numbers where the a decimal place repeats indefinitely,

0.33333\dots

0.\overline{3}

is a repeating decimal.
The bar above the digit

3

means that

3

is repeating.
Repeating decimals can be represented as a fraction.

0.\overline{3}

is the same as

\cfrac{1}{3}

Non-repeating, non-terminating decimals are decimal numbers that
cannot be represented as a fraction.

\pi ,

(pi) is a non-repeating, non-terminating decimal.

\sqrt{5}

( square root of

5

) is a non-repeating, non-terminating decimal.

Square and Cube Numbers


A square number is the result of multiplying a number by itself. For example: $1 \times 1 = 1 → 1$ is a square number $2 \times 2 = 4 → 4$ is a square number $3 \times 3 = 9 → 9$ is a square number $1 \times 1$ can be written in a shorter way, using an exponent. $1^2$ $2 \times 2$ can be written in a shorter way, using an exponent $2^2$ $3 \times 3$ can be written is a shorter way, using an exponent $3^2$	A cube number is the result of multiplying an integer by itself three times. For example: $1 \times 1 \times 1 = 1 → 1$ is a cube number $2 \times 2 \times 2 = 8 → 8$ is a cube number $3 \times 3 \times 3 = 27 → 27$ is a cube number $1 \times 1 \times 1$ can be written in a shorter way, using an exponent. $1^3$ $2 \times 2 \times 2$ can be written in a shorter way, using an exponent $2^3$ $3 \times 3 \times 3$ can be written is a shorter way, using an exponent $3^3$

A square number is the result of multiplying a number by itself.

For example:

1 \times 1 = 1 → 1

is a square number

2 \times 2 = 4 → 4

is a square number

3 \times 3 = 9 → 9

is a square number

1 \times 1

can be written in a shorter way, using an exponent.

1^2

2 \times 2

can be written in a shorter way, using an exponent

2^2

3 \times 3

can be written is a shorter way, using an exponent

3^2

A cube number is the result of multiplying an integer by itself three times.

For example:

1 \times 1 \times 1 = 1 → 1

is a cube number

2 \times 2 \times 2 = 8 → 8

is a cube number

3 \times 3 \times 3 = 27 → 27

is a cube number

1 \times 1 \times 1

can be written in a shorter way, using an exponent.

1^3

2 \times 2 \times 2

can be written in a shorter way, using an exponent

2^3

3 \times 3 \times 3

can be written is a shorter way, using an exponent

3^3

Reciprocals


The reciprocal of a number is the multiplicative inverse of a number. Meaning that when the reciprocal of a number (multiplicative inverse) is multiplied to the given number, the result is $1.$ For example, the reciprocal of $5$ is $\, \cfrac{1}{5}.$ $5$ can be written as $\, \cfrac{5}{1} \,$ to find the reciprocal, flip the numerator and the denominator. So, $\, \cfrac{5}{1} \,$ will become $\, \cfrac{1}{5}.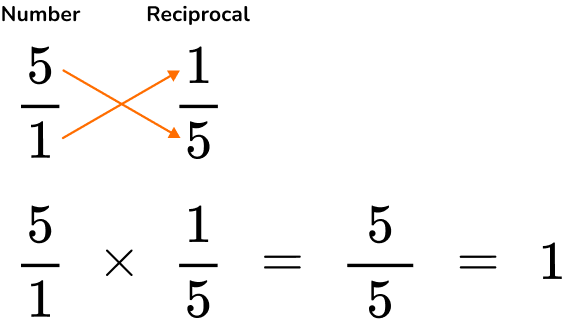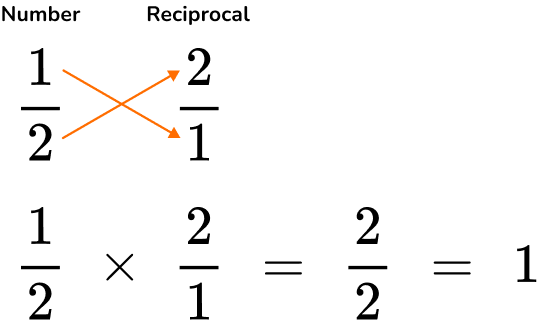$ The reciprocal of $\, \cfrac{1}{2} \,$ is $\, \cfrac{2}{1}.$

The reciprocal of a number is the multiplicative inverse of a number. Meaning that when the reciprocal of a number (multiplicative inverse) is multiplied to the given number, the result is

1.

For example, the reciprocal of

5

\, \cfrac{1}{5}.

5

can be written as

\, \cfrac{5}{1} \,

to find the reciprocal, flip the numerator and the denominator.
So,

\, \cfrac{5}{1} \,

will become

\, \cfrac{1}{5}.

The reciprocal of

\, \cfrac{1}{2} \,

\, \cfrac{2}{1}.

What are types of numbers?

Common Core State Standards

How does this relate to Kindergarten through 6th grade?

Kindergarten – Counting and Cardinality (K.CC.B.4.c)
Understand that each successive number name refers to a quantity that is one larger

Grade 1 – Number and Operations Base Ten (1.NBT.A.1)
Count to $120,$ starting at any number less than $120.$ In this range, read and write numerals and represent a number of objects with a written numeral.

Grade 2 – Number and Operations Base Ten (2.NBT.A.1)
Understand that the three digits of a three-digit number represent amounts of hundreds, tens, and ones; e.g., $706$ equals $7$ hundreds, $0$ tens, and $6$ ones.

Grade 3 – Number and Operation – Fractions (3.NF.A.1)
Understand a fraction $\cfrac{1}{b}$ as the quantity formed by $1$ part when a whole is partitioned into $b$ equal parts; understand a fraction $\cfrac{a}{b}$ as the quantity formed by a parts of size $\cfrac{1}{b}.$

Grade 4 – Number and Operations Base Ten (4.NBT.A.2)
Read and write multi-digit whole numbers using base-ten numerals, number names, and expanded form. Compare two multi-digit numbers based on meanings of the digits in each place, using $>, =,$ and $<$ symbols to record the results of comparisons.

Grade 5 – Number and Operations Base Ten (5.NBT.A.3)
Read, write, and compare decimals to thousandths.

Grade 6 – Number System (6.NS.C)
Apply and extend previous understandings of numbers to the system of rational numbers.

Grade 6 – Expressions and Equations (6.EE.A.1)
Write and evaluate numerical expressions involving whole-number exponents.

How to determine the type of a number

In order to classify a number:

Recall the definition of the type of number needed.
Show that the number fits or does not fit in the number set or definition.

In order to find the reciprocal of a number:

Identify the numerator and denominator of the given number.
Flip the numerator and the denominator.
Multiply the given number to the reciprocal to check that the product is $1$ .

Types of number examples

Example 1: rational numbers

Is $1\cfrac{3}{4} \,$ a rational number?

Recall the definition of the type of number needed.

By definition, a rational number is any number that can be expressed as a fraction where the numerator and denominator are integers.

2Show that the number fits or does not fit in the number set or definition.

$1\cfrac{3}{4} \,$ is a mixed number. A mixed number can be written as an improper fraction.

The model shows $1\cfrac{3}{4}.$

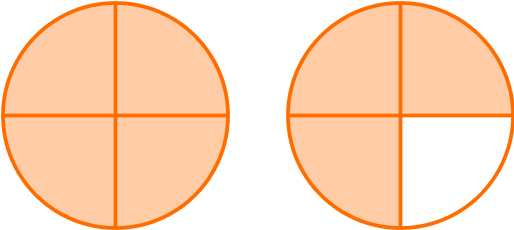
The first circle model shows $4$ shaded parts out of $4$ equal parts, which is $\, \cfrac{4}{4} \,$ or $1.$

The second model shows $3$ shaded parts out of $4$ equal parts which $\, \cfrac{3}{4}.$

$\cfrac{4}{4}+\cfrac{3}{4}=\cfrac{7}{4}$

$\cfrac{7}{4} \,$ is a rational number because the numerator and the denominator are both whole numbers

$\cfrac{7}{4} \,$ is the same as $1\cfrac{3}{4} \, →$ is in the rational number set

Also, rational numbers include all positive and negative mixed numbers.

Example 2: prime numbers

Determine whether the number $23$ is a prime number.

Recall the definition of the type of number needed.

The definition of a prime number is any positive whole number that has only two factors, $1$ and itself.

Show that the number fits or does not fit in the number set or definition.

The factors of $23$ are $1$ and $23.$ $23$ is a prime number.

Step-by-step guide: Prime numbers

Example 3: odd numbers

Is $15$ an odd number?

Recall the definition of the type of number needed.

Odd numbers are not divisible by $2$ without remainders and end in $1, 3, 5, 7,$ or $9.$

Show that the number fits or does not fit in the number set or definition.

$15$ ends in a $5,$ it is an odd number.

Example 4: reciprocals

Find the reciprocal of $14.$

Identify the numerator and denominator of the given number.

$14$ can be written a the fraction $\, \cfrac{14}{1} \,$ because all whole numbers can be written in this form.

The numerator is $14$ and the denominator is $1.$

Flip the numerator and the denominator.

$\cfrac{14}{1} \,$ will become $\, \cfrac{1}{14}.$

The numerator becomes the denominator and the denominator becomes the numerator.

Multiply the given number by the reciprocal to check that the product is $1$ .

$\cfrac{14}{1}\times \cfrac{1}{14} = \cfrac{14}{14}=1$

The product of a number and its reciprocal is always $1.$

Example 5: square numbers

Determine if $16$ is a square number.

Recall the definition of the type of number needed.

A square number is the result of multiplying an integer by itself.

Let’s start with $1.$

$\begin{aligned} &1 \times 1 = 1 \\ &2 \times 2 = 4 \\ &3 \times 3 = 9 \\ &4 \times 4 = 16 \end{aligned}$

Show that the number fits or does not fit in the number set or definition.

$16 = 4\times 4$ . $16$ is a square number.

Example 6: repeating decimal

Show that $\cfrac{2}{9}$ is a repeating decimal.

Recall the definition of the type of number needed.

The definition of a repeating decimal is any decimal where the decimal places repeat indefinitely.

Show that the number fits or does not fit in the number set or definition.

A fraction can be seen as division where the numerator is the dividend, the denominator is the divisor, and the fraction bar is the division bar.

$\cfrac{2}{9} \,$ is the same as $2 \div 9.$ Long division is used to divide the numbers.

You can see the repeating pattern in the division and in the answer.

This means that $\cfrac{2}{9}=0.22…=0.\overline{2}.$

Teaching tips for types of numbers

Use the Venn Diagram to help students make connections between the different types of number sets.

The number sets build upon themselves from the very first set of numbers they work with which is natural numbers. This will help students understand that natural numbers, whole numbers and integers are all considered to be rational numbers too.

Using a calculator is helpful when showing elementary students repeating decimals.

Reinforce to students that the cardinal numbers and positive integers are the same as the set of natural numbers.

Easy mistakes to make

Mixing up the definitions
It is common to mix up definitions. For example, assuming that whole numbers are natural numbers and vice versa
Example: Whole numbers include $0$ and natural numbers do not.

Thinking zero is a natural number
Zero is not a natural number. The natural numbers are considered to be the counting the numbers and starting with $1.$

Thinking whole numbers are not rational numbers
Rational numbers are numbers that can be expressed as a fraction where the numerator and the denominator are integers. The number $3$ is rational because we can express $3$ as the fraction $\, \cfrac{3}{1}.$

Thinking that $2$ is not a prime number
Students often think that prime numbers have to be odd numbers. $2$ is a prime number and an even number.

Practice types of numbers questions

Natural numbers, whole numbers, integers, rational numbers

Only natural numbers

Only whole numbers

Only even numbers

Natural numbers are the positive whole numbers.

$22$ is a natural number.

Whole numbers are the natural numbers plus $0.$

$22$ is a whole number.

Integers are positive and negative whole numbers.

$22$ is an integer.

Rational numbers are numbers that can be written as a fraction where the numerator and denominator are whole numbers.

$22$ can be written as $\, \cfrac{22}{1}$ so, $22$ is also a rational number.

Composite Number

Whole number

Rational number

Even number

$1\cfrac{1}{5} \,$ is a mixed number. A mixed number can be written as an improper fraction.

The model shows $1\cfrac{1}{5}$

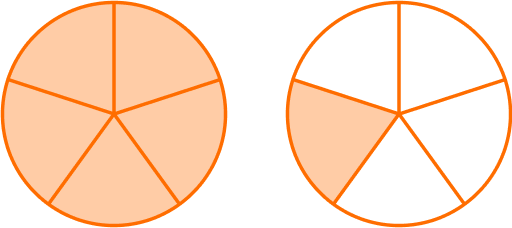
Types Of Numbers practice question 2

The first model shows $5$ shaded parts out of $5$ equal parts.

The second model shows $1$ shaded part out of $5$ equal parts.

\cfrac{5}{5}+ \cfrac{1}{5}= \cfrac{6}{5}

$\cfrac{6}{5} \,$ is a rational number because the numerator and the denominator are both whole numbers.

$\cfrac{6}{5} \,$ is the same as $1\cfrac{1}{5} \,$ is a rational number.

Also, rational numbers include all positive and negative mixed numbers.

By definition, a rational number is any number that can be expressed as a fraction where the numerator and denominator are integers.

The rational number set includes all positive and negative fractions, decimals, repeating decimals, and integers.

Improper fraction

Prime number

Composite number

Odd number

$2$ is a prime number because it only has two factors $1$ and $2.$

1 \times 2 = 2

\cfrac{2}{3}

\cfrac{1}{3}

\cfrac{3}{2}

\cfrac{1}{2}

$\cfrac{2}{3} \,$ has a numerator of $2$ and the denominator of $3.$

To find the reciprocal flip the numerator and the denominator where the numerator becomes the denominator and the denominator becomes the numerator.

So, the reciprocal of $\, \cfrac{2}{3} \,$ is $\, \cfrac{3}{2}$

\cfrac{2}{3}\times \cfrac{3}{2}= \cfrac{6}{6}=1

Terminating decimal

Non-terminating decimal

Composite number

Repeating decimal

$0.\overline{4}$ means $0.\4444444…$

The bar above the number $4$ in this decimal means repeating.

So, $0.\overline{4}$ is a repeating decimal.

Prime number

Square number

Even Number

Proper fraction

A square number is a number multiplied to itself.

$5 \times 5 = 25,$ so $25$ is a square number.

Types of numbers FAQs

Is $0$ a natural number?

$0$ is not a natural number. $0$ is a whole number. The natural numbers are considered the counting numbers, which begin with $1.$

Are there any even prime numbers?

Yes, $2$ is the only even prime number. $2$ has exactly two factors, itself and $1.$

Are all decimals considered rational numbers?

Not all decimals are rational numbers. Only the decimals that can be written as a fraction are considered rational numbers.

Is there another way to figure out perfect square numbers and perfect cube numbers?

Yes, in middle school you will learn how to take the square root and the cube root of numbers.

Are there any other classification of numbers besides rational and irrational numbers?

Yes, in algebra $1$ and algebra $2,$ you will learn about complex numbers, which are real numbers and imaginary numbers. Complex numbers are made up of a real part and an imaginary part.

The next lessons are

Still stuck?

At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.

Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.