Factors

[FREE] Fun Math Games & Activities Packs

Always on the lookout for fun math games and activities in the classroom? Try our ready-to-go printable packs for students to complete independently or with a partner!

DOWNLOAD FREE

In order to access this I need to be confident with:

Commutative property

Understanding multiplication

Whole numbers Prime numbers

Math resources Number and quantity Factors and multiples

Factors

Here you’ll learn about factors, including recognizing factors, the commutative property, how to find all factor pairs of a given number, and solving problems using factors.

Students will first learn about factors as part of operations and algebraic thinking in elementary school.

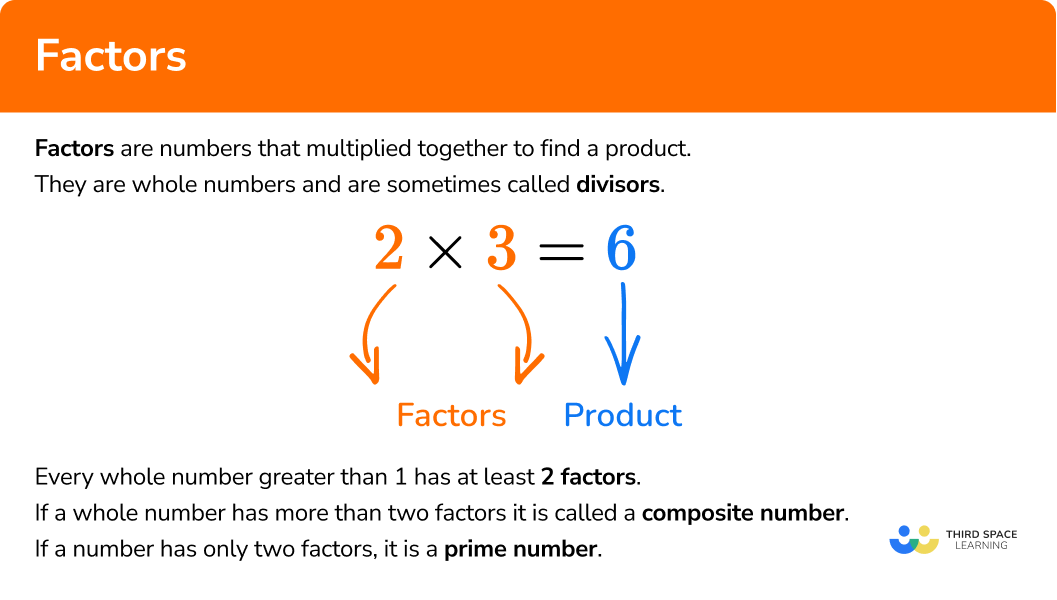
What are factors?

Factors are numbers that multiplied together to find a product. They are whole numbers and can sometimes be called divisors.

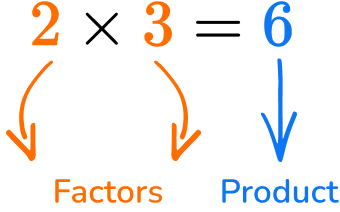
Every whole number greater than $\bf{1}$ has at least $\bf{2}$ factors.

If a whole number has more than two factors it is called a composite number.

If a number has only two factors, it is a prime number.

Step-by-step guide: Prime & composite numbers

A factor pair is two numbers that are multiplied to create a product.

For example, here are the factor pairs of $12.$

Factor Pair	Array (row × columns)	Product
$1\times{12}$		$12$
$2\times{6}$		$12$
$3\times{4}$		$12$

Factor pairs have a commutative property which means you can switch the order and the product is the same.

For example,

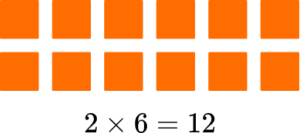
Prime factors are factors of a number that are also prime numbers

For example, the prime factors of $30=2\times{3}\times{5}.$

Step-by-step guide: Prime factors

Factors are very useful. You can use them to find common denominators, calculating areas and simplify algebraic expressions in upper grades!

What are factors?

Common Core State Standards

How does this relate to 3rd grade math and 4th grade math?

Grade 3: Operations & Algebraic Thinking (3.OA.B.5)
Apply properties of operations as strategies to multiply and divide.

Grade 4: Operations & Algebraic Thinking (4.OA.B.4)
Find all factor pairs for a whole number in the range $1-100.$ Recognize that a whole number is a multiple of each of its factors. Determine whether a given whole number in the range $1-100$ is a multiple of a given one-digit number. Determine whether a given whole number in the range $1-100$ is prime or composite.

How to list factors

In order to list all of the factor pairs of a given number:

State the pair $\bf{1} \, \textbf{×} \,$ the number.
Write the next smallest factor of the number and calculate its factor pair.
Repeat until the next factor pair is the same as the previous pair.
Write out the list of factors for a number.

[FREE] Factors Worksheet (Grades 4 & 5)

Use this worksheet to check your grade 4 and 5 students’ understanding of factors. 15 questions with answers to identify areas of strength and support!

DOWNLOAD FREE

[FREE] Factors Worksheet (Grades 4 & 5)

Use this worksheet to check your grade 4 and 5 students’ understanding of factors. 15 questions with answers to identify areas of strength and support!

DOWNLOAD FREE

Factors examples

Example 1: listing factors (even number)

List the factors of $24.$

State the pair $\bf{1} \, \textbf{×} \,$ the number.

The factor pair is $1\times{24}.$

2Write the next smallest factor of the number and calculate its factor pair.

As $24$ is an even number, $2$ is a factor of $24.$

24\div{2}=12

so the next factor pair is

2\times{12}.

3Repeat until the next factor pair is the same as the previous pair.

So far there is:

\begin{aligned} 1\times{24}\\ 2\times{12} \end{aligned}

24\div{3}=8

and so the next factor pair is

3\times{8}

24\div{4}=6

and so the next factor pair is

4\times{6}

24\div{5}=4.8

which is a decimal so $5$ is not a factor of $24$

The next factor to try is $6.$ As factors are commutative,

6\times{4}=4\times{6}

which is the same as the previous factor pair.

Now all of the factor pairs have been found:

\begin{aligned} &1\times{24}\\ &2\times{12}\\ &3\times{8}\\ &4\times{6} \end{aligned}

4Write out the list of factors for the given number.

Reading down the first column of factors, and up the second column, the factors of $24$ are: $1, 2, 3, 4, 6, 8, 12, 24.$

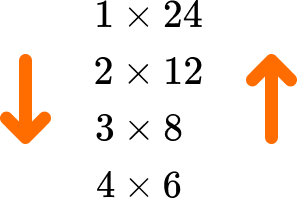
Example 2: listing factors (odd number)

List the factors of $27.$

State the pair $\bf{1} \, \textbf{×} \,$ the number.

The number $= \, 27$ we have the first factor pair

$1\times{27}.$

Write the next smallest factor of the number and calculate its factor pair.

As $27$ is an odd number, $2$ is not a factor of $27.$

However, $27\div{3}=9$

and so the next factor pair is

$3\times{9}.$

Repeat until the next factor pair is the same as the previous pair.

So far we have:

$\begin{aligned} &1\times{27}\\ &3\times{9} \end{aligned}$

$27$ has a remainder when it is divided by $4, 5, 6, 7,$ or $8.$

The next factor to try is $9,$ but we already know that $3\times{9}$ is a factor pair and this is the same as $9\times{3}.$

We have now found all of the factor pairs:

$\begin{aligned} &1\times{27}\\ &3\times{9} \end{aligned}$

Write out the list of factors for the given number.

Reading down the first column of factors, and up the second column, the factors of $27$ are: $1, 3, 9,$ and $27.$

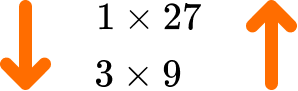
Example 3: listing factors when there is a repeated factor

List the factors of $36.$

State the pair $\bf{1} \, \textbf{×} \,$ the number.

The number $= \, 36$ we have the first factor pair

$1\times{36}.$

Write the next smallest factor of the number and calculate its factor pair.

As $36$ is an even number, $2$ is a factor of $36.$

$36\div{2}=18$

and so the next factor pair is

$2\times{18}.$

Repeat until the next factor pair is the same as the previous pair.

So far we have:

$\begin{aligned} &1\times{36}\\ &2\times{18} \end{aligned}$

$36\div{3}=12$

and so the next factor pair is

3\times{12}

$36\div{4}=9$

and so the next factor pair is

4\times{9}

$36$ has a remainder when it is divided by $5$ and so $5$ is not a factor.

$36\div{6}=6$

and so the next factor pair is

6\times{6}

We have reached a repeated factor and so we have found all of the factor pairs for $36:$

$\begin{aligned} &1\times{36}\\ &2\times{18}\\ &3\times{12}\\ &4\times{9}\\ &6\times{6} \end{aligned}$

Write out the list of factors for the given number.

Reading down the first column of factors, and up the second column, the factors of $36$ are: $1, 2, 3, 4, 6, 9, 12, 18,$ and $36.$

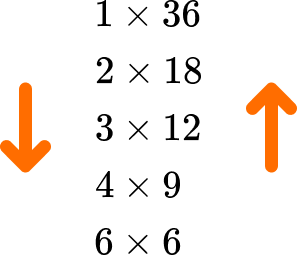
Example 4: listing factors (prime number)

List the factors of $7.$

State the pair $\bf{1} \, \textbf{×} \,$ the number.

The number $= \, 7$ we have the first factor pair

$1\times{7}.$

Write the next smallest factor of the number and calculate its factor pair.

As $7$ is an odd number, $2$ is not a factor of $7.$

$7$ has a remainder when it is divided by $2, 3, 4, 5,$ and $6.$

Repeat until the next factor pair is the same as the previous pair.

The next whole number to try is $7,$ which we have already used

$(1\times{7}=7\times{1})$

and so the only factor pair for the number $7$ is

$1\times{7}.$

Write out the list of factors for the given number.

The factors of $7$ are: $1$ and $7.$

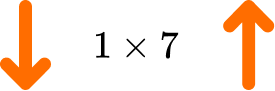
As $7$ has only two factors, $1$ and itself, $7$ is a prime number.

Example 5: listing factors of any number (3 digit number)

List the factors of $200.$

State the pair $\bf{1} \, \textbf{×} \,$ the number.

The number $= \, 200$ we have the first factor pair

$1\times{200}.$

Write the next smallest factor of the number and calculate its factor pair.

As $200$ is an even number, $2$ is a factor of $200.$

$200\div{2}=100$

and so the next factor pair is

$2\times{100}.$

Repeat until the next factor pair is the same as the previous pair.

So far we have:

$\begin{aligned} &1\times{200}\\ &2\times{100} \end{aligned}$

$200$ has a remainder when it is divided by $3$ and so $3$ is not a factor.

$200\div{4}=50$

and so the next factor pair is

4\times{50}.

$200\div{5}=40$

and so the next factor pair is

5\times{40}.

$200$ has a remainder when it is divided by $6$ and $7$ and so these are not factors of $200.$

$200\div{8}=25$

and so the next factor pair is

8\times{25}.

$200$ has a remainder when it is divided by $9$ and so $9$ is not a factor.

$200\div{10}=20$

and so the next factor pair is

10\times{20}.

$200$ has a remainder when it is divided by $11, 12, 13, 14, 15, 16, 17, 18,$ and $19$ and so these are not factors of $200.$

The next integer to try is $20$ but this appears in the previous factor pair

$(10\times{20}=20\times{10}).$

We have therefore found all of the factor pairs for $200:$

$\begin{aligned} 1&\times{200}\\ 2&\times{100}\\ 4&\times{50}\\ 5&\times{40}\\ 8&\times{25}\\ 10&\times{20} \end{aligned}$

Write out the list of factors for the given number.

Reading down the first column of factors, and up the second column, the factors of $200$ are: $1, 2, 4, 5, 8, 10, 20, 25, 40, 50, 100,$ and $200.$

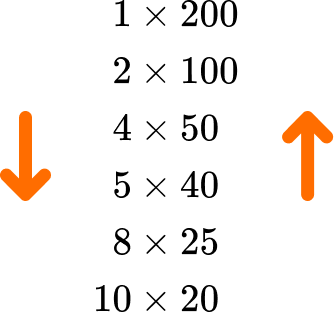
Example 6: using factors to solve word problems

A store needs $18$ boxes of crackers. The boxes need to be stacked with the same number of boxes in each row. There needs to be more than $1$ row of boxes and less than $18$ rows. How many different ways can the rows be created?

State the pair $\bf{1} \, \textbf{×} \,$ the number.

$1 \times 18$ is the first factor pair. However, this will not be used because there needs to be more than $1$ row of boxes.

Write the next smallest factor of the number and calculate its factor pair.

$18$ is an even number, $2$ is a factor of $9.$

$9\times{2}=18,$ which means there can be $9$ rows of $2$ boxes

$2\times{9}=18,$ which means there can be $2$ rows of $9$ boxes.

$9$ rows of $2$ boxes is different from $2$ rows of $9$ boxes.

Repeat until the next factor pair is the same as the previous pair.

$18$ does not have a remainder when it is divided by $3. \, 3$ is a factor of $18.$

$3 \times 6=18,$ which means there can be $3$ rows of $6$ boxes.

$6 \times 3=18,$ which means there can be $6$ rows of $3$ boxes.

Write out the list of factors for the given number.

There are 4 different ways the rows can be created.

$2$ rows $\times \; 9$ columns

$9$ rows $\times \; 2$ columns

$3$ rows $\times \; 6$ columns

$6$ rows $\times \; 3$ columns

Teaching tips for finding factors

Identifying factors is usually more difficult for students than finding multiples. Using manipulatives helps students to find positive factors, such as counters.

Visual models such as arrays help students to organize the positive factors of the original number.

Have students identify patterns when finding factors. Hundreds charts and multiplication tables are very helpful to students in identifying patterns of factors.

Our favorite mistakes

Confusing factors and multiples
Factors are two or more whole numbers multiplied, like $5 \times 4.$ Multiples are the products of factors, like the multiples of $5$ are $5, 10, 15, 20.$

Remember $\bf{1}$ and the number itself are factors
All numbers are a factor of themselves and $1$ is a factor of every number.
For example, the factors of $6$ are: $1, 2, 3, 6$ and so $6$ is a factor of itself.

Practice factors questions

12, 24, 36, 48, 60

$1$ and $12, 2$ and $6$

2\times{2}\times{3}

1, 2, 3, 4, 6, 12

The factor pairs of $12$ are:

\begin{aligned} 1&\times{12}\\ 2&\times{6}\\ 3&\times{4} \end{aligned}

So the factors of $12$ are $1, 2, 3, 4, 6$ and $12.$

1, 3, 5, 15

15, 30, 45, 60, 75, 90

$3$ and $5$

3\times{5}

The factor pairs of $15$ are:

\begin{aligned} 1&\times{15}\\ 3&\times{5} \end{aligned}

So the factors of $15$ are $1, 3, 5,$ and $15.$

$1$ and $64, 2$ and $32$

8, 64, 128, 192, 256, 320

1, 2, 4, 8, 16, 32, 64

2\times{2}\times{2}\times{2}\times{2}\times{2}

The factor pairs of $64$ are:

\begin{aligned} 1&\times{64}\\ 2&\times{32}\\ 4&\times{16}\\ 8&\times{8} \end{aligned}

So the factors of $64$ are $1, 2, 4, 8, 16, 32,$ and $64.$

17, 34, 51, 68, 85, 102

17

1

$1$ and $17$

The factor pairs of $17$ are:

1\times{17}

So the factors of $17$ are $1$ and $17.$

2\times{2}\times{2}\times{3}\times{5}

$12$ and $10, 6$ and $20, 4$ and $30.$

1, 2, 3, 4, 5, 6, 8, 10, 12, 15, 20, 24, 30, 40, 60, 120

240, 360, 480, 600

The factor pairs of $120$ are:

\begin{aligned} 1&\times{120}\\ 2&\times{60}\\ 3&\times{40}\\ 4&\times{30}\\ 5&\times{24}\\ 6&\times{20}\\ 8&\times{15}\\ 10&\times{12} \end{aligned}

So the factors of $120$ are $1, 2, 3, 4, 5, 6, 8, 10, 12, 15, 20, 24, 30, 40, 60$ and $120.$

$3$ rows $\times \; 4$ columns

$12$ rows $\times \; 1$ column

$1$ row $\times \; 12$ columns

$24$ rows $\times \; 2$ columns

The factor pairs of $12$ are:

\begin{aligned} 1&\times{12}\\ 12&\times{1}\\ 2&\times{6}\\ 6&\times{2}\\ 3&\times{4}\\ 4&\times{3} \end{aligned}

Since there has to be more than $1$ row and less than $12$ rows, the only factor pair that would work is $3$ rows $\times \; 4$ columns.

Factors FAQ

Do you have to have all divisibility rules memorized to find factors of numbers?

Knowing divisibility rules is very helpful when finding factors. However, using the steps to find factors is also a helpful tool.

Are factors and multiples the same thing?

No, factors and multiples are not the same. Factors are two or more whole numbers multiplied together that give a product. In other words, a factor divides a number and leaves no remainder. A multiple is the product when one number is multiplied by another number.

Are factors always positive?

No, factors can be negative numbers. However, in elementary school students typically work only with positive numbers.

Are factors and quotients the same thing?

No, a quotient is the number resulting from division. A factor divides another number leaving no remainder.

Do factor pairs have to be prime factors?

No, factor pairs are any two whole numbers that multiply to the given number.

The next lessons are

Still stuck?

At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.

Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.