[FREE] Fun Math Games & Activities Packs

Always on the lookout for fun math games and activities in the classroom? Try our ready-to-go printable packs for students to complete independently or with a partner!

DOWNLOAD FREE

In order to access this I need to be confident with:

Exponents Prime and composite numbers Types of numbers

Math resources Number and quantity Factors and multiples

GCF

Greatest common factor

Here you will learn about the greatest common factor, including a review of prime factorization and how to use it to find the greatest common factor.

Students will first learn about the greatest common factor as part of the number system in 6th grade.

What is the greatest common factor?

The greatest common factor (GCF) is the largest integer that two or more numbers can both be divided by. The name itself tells you what the skill is:

For example,

Find the greatest common factor of $4$ and $6.$

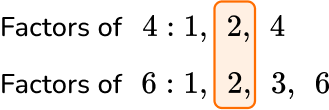
By listing the factors of $4$ and the factors of $6,$ you can see that the greatest number that occurs in each list is $2,$ so the greatest common factor of $4$ and $6$ is $2$ .

You may have noticed that $1$ occurs in both lists. This is a common factor, but not the greatest common factor.

The Prime Factorization Method

Calculating the greatest common factor becomes more complicated for larger numbers. Listing all the factors of each number can be time consuming and it is easy to forget a factor.

To make it simpler, you can use the prime factors of both numbers. You can use prime factors and a Venn diagram to calculate the Greatest Common Factor.

You need to write out the prime factorization of each number fully and then put the numbers into the Venn diagram by looking for pairs.

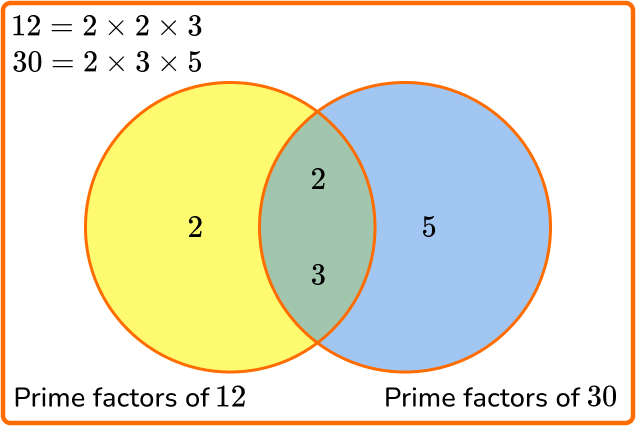
Here, you have the prime factors of $12$ and $30.$

The yellow section represents the prime factors of $12$ that are not prime factors of $30$ (which is just the value $2$ ).
The blue section represents the prime factors of $30$ that are not prime factors of $12$ (which is just the value $5$ ).
The green intersection represents the shared prime factors of $12$ and $30.$ Here, the prime factors of $2$ and $3$ occur for both $12$ and $30.$ Their product is the greatest common factor.

The greatest common factor for $12$ and $30$ is $2 \times 3 = 6.$

What is the greatest common factor?

Common Core State Standards

How does this relate to 6th grade math?

Grade 6 – The Number System (6.NS.B.4)
Find the greatest common factor of two whole numbers less than or equal to $100$ and the least common multiple of two whole numbers less than or equal to $12.$ Use the distributive property to express a sum of two whole numbers $1-100$ with a common factor as a multiple of a sum of two whole numbers with no common factor. For example, express $36 + 8$ as $4 (9 + 2).$

How to calculate the greatest common factor (GCF)

In order to calculate the greatest common factor for two or more numbers:

State the product of prime factors for each number.
Write all the prime factors into the Venn diagram for each number.
Multiply the prime factors in the intersection to find the GCF.

[FREE] Greatest Common Factor Worksheet (Grades 6 to 8)

Use this worksheet to check your grade 6 to 8 students’ understanding of greatest common factors. 15 questions with answers to identify areas of strength and support!

DOWNLOAD FREE

[FREE] Greatest Common Factor Worksheet (Grades 6 to 8)

Use this worksheet to check your grade 6 to 8 students’ understanding of greatest common factors. 15 questions with answers to identify areas of strength and support!

DOWNLOAD FREE

Greatest common factor examples

Example 1: two simple composite numbers

Calculate the greatest common factor of $18$ and $24.$

State the product of prime factors for each number.

$\begin{aligned} & 18=2 \times 3 \times 3 \\\\ & 24=2 \times 2 \times 2 \times 3 \end{aligned}$

2Write all the prime factors into the Venn diagram for each number.

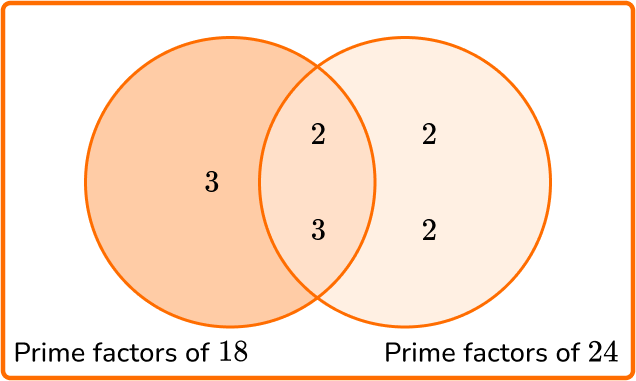
3Multiply the prime factors in the intersection to find the GCF.

GCF $= 2 \times 3=6$

Example 2: one composite number is a factor of the other

Calculate the greatest common factor of $14$ and $56.$

State the product of prime factors for each number.

$\begin{aligned} & 14=2 \times 7 \\\\ & 56=2 \times 2 \times 2 \times 7 \end{aligned}$

Write all the prime factors into the Venn diagram for each number.

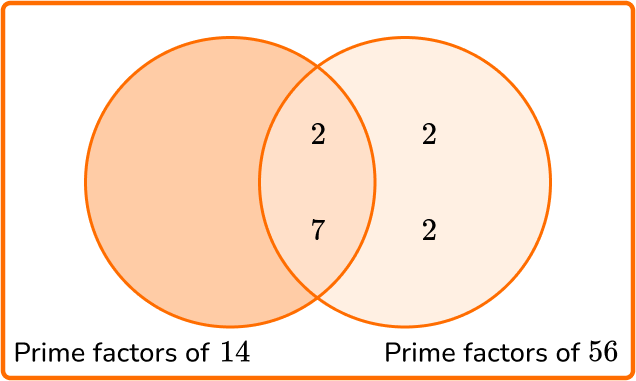
Multiply the prime factors in the intersection to find the GCF.

GCF $=2 \times 7=14$

Example 3: calculate the prime factorization first

Given that $90=2 \times 3^2 \times 5,$ calculate the greatest common factor of $54$ and $90.$

State the product of prime factors for each number.

To state the product of prime factors of $54,$ you use a factor tree:

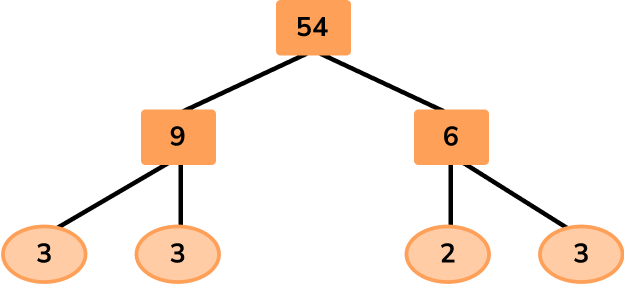
$\begin{aligned} & 54=2 \times 3 \times 3 \times 3 \\\\ & 90=2 \times 3 \times 3 \times 5 \end{aligned}$

Write all the prime factors into the Venn diagram for each number.

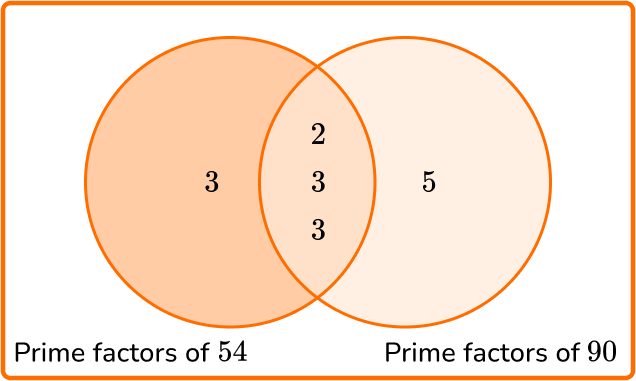
Multiply the prime factors in the intersection to find the GCF.

GCF $=2 \times 3 \times 3=18$

Example 4: three composite numbers

Calculate the greatest common factor of $12, 20,$ and $32.$

State the product of prime factors for each number.

$\begin{aligned} & 12=2 \times 2 \times 3 \\\\ & 20=2 \times 2 \times 5 \\\\ & 32=2 \times 2 \times 2 \times 2 \times 2 \end{aligned}$

Write all the prime factors into the Venn diagram for each number.

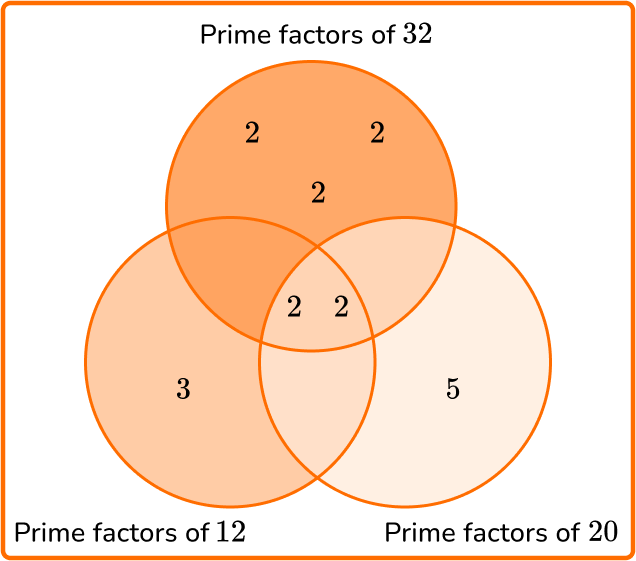
Multiply the prime factors in the intersection to find the GCF.

GCF $=2 \times 2=4$

Example 5: only common factor is 1

Calculate the greatest common factor of $35$ and $72.$

State the product of prime factors for each number.

$\begin{aligned} & 35=5 \times 7 \\\\ & 72=2 \times 2 \times 2 \times 3 \times 3 \end{aligned}$

Write all the prime factors into the Venn diagram for each number.

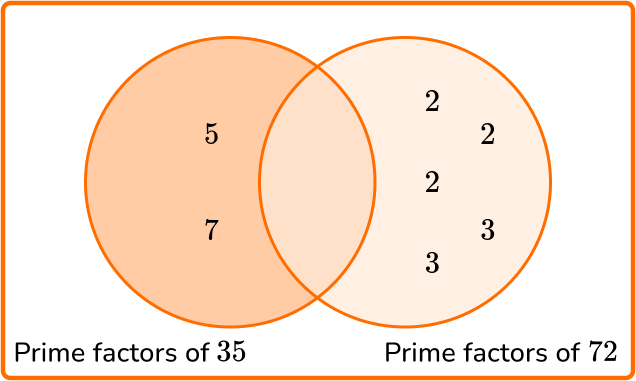
Multiply the prime factors in the intersection to find the GCF.

Here there are no prime factors in the intersection, so the greatest common factor is $1.$

Example 6: word problem

Sue sells apples in baskets. On Thursday, she expects to receive a delivery of $36$ apples in the morning and $42$ apples in the afternoon. Sue wants to divide each crate equally into smaller baskets, so she has the same number of apples in each basket.

What is the maximum number of apples she can put in each basket so that they contain the same quantity during the whole day?

State the product of prime factors for each number.

$\begin{aligned} & 36=2 \times 2 \times 3 \times 3 \\\\ & 42=2 \times 3 \times 7 \end{aligned}$

Write all the prime factors into the Venn diagram for each number.

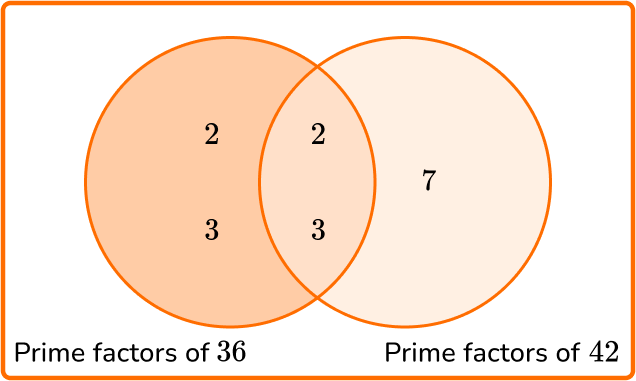
Multiply the prime factors in the intersection to find the GCF.

GCF $=2 \times 3=6$

To answer the question: She should put $6$ apples in each basket.

Teaching tips for greatest common factor

Start with small numbers, so students can focus on understanding and learning the procedure. Then, move to large numbers to challenge students’ ability to find all the prime factors of a number.

Instead of relying only on worksheets, look for opportunities for students to solve real-world problems that involve GCF.

Some students may struggle to find all the prime factors, especially for larger numbers. You may provide a calculator to assist students so that they can focus on the skill, not on the calculations.

Our favorite mistakes

Calculating the least common multiple (LCM) instead of GCF
It is common to mix up the greatest common factor with the least common multiple. To avoid this, remember the definition of factors and multiples.
Factor: the number being multiplied
Multiple: the product of two or more factors being multiplied
For example,
What is the GCF of $2$ and $10?$ What is the LCM of $2$ and $10?$
Factors of $2\text{:} \; 1, 2$ Multiples of $2\text{:} \; 2, 4, 6, 8, 10…$
Factors of $10\text{:}\; 1, 2, 5, 10$ Multiples of $10\text{:}\; 10, 20, 30…$
The GCF is $2$ The LCM is $10$

Not writing duplicate factors in the Venn diagram
It is possible to forget to include prime factors in a Venn diagram when the factors are repeated.
For example,
What is the GCF of $54$ and $81?$

Greatest common factor practice questions

1

660

11

2

\begin{aligned} &22= 2 \times 11\\\\ &60=2 \times 2 \times 3 \times 5 \end{aligned}

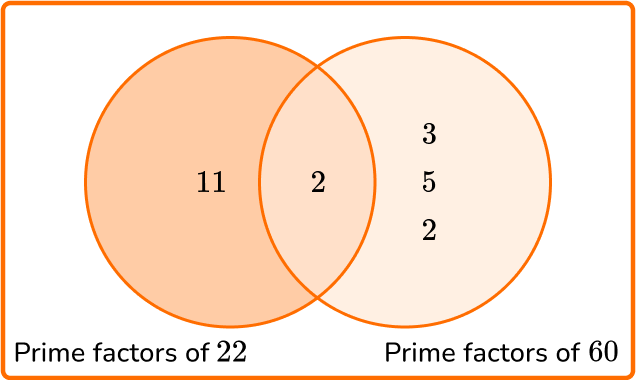
Greatest Common Factor Practice Question 1

GCF $= 2$

3

7

21

63

\begin{aligned} &21=3 \times 7\\\\ &63= 3 \times 3 \times 7 \end{aligned}

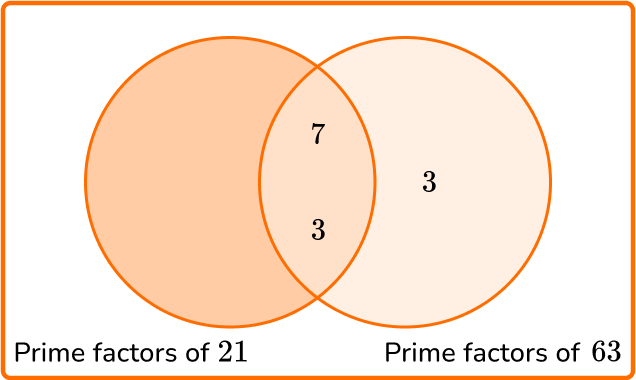
Greatest Common Factor Practice Question 2

GCF $=7 \times 3=21$

45

15

1

270

\begin{aligned} &90= 2 \times 3 \times 3 \times 5\\\\ &135=3 \times 3 \times 3 \times 5 \end{aligned}

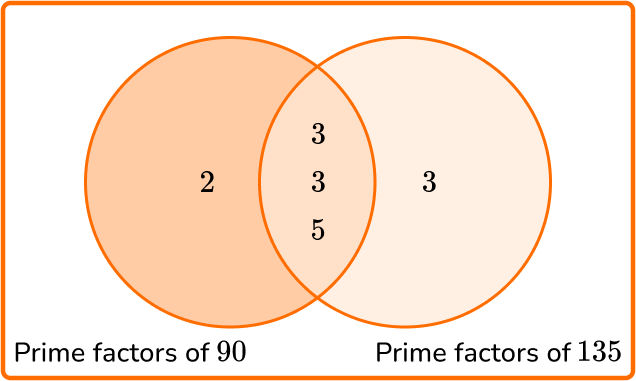
Greatest Common Factor Practice Question 3

GCF $=3\times 3 \times 5=45$

12

2

3

6

\begin{aligned} &12=2 \times 2 \times 3\\\\ &30=2 \times 3 \times 5\\\\ &48=2 \times 2 \times 2 \times 2 \times 3 \end{aligned}

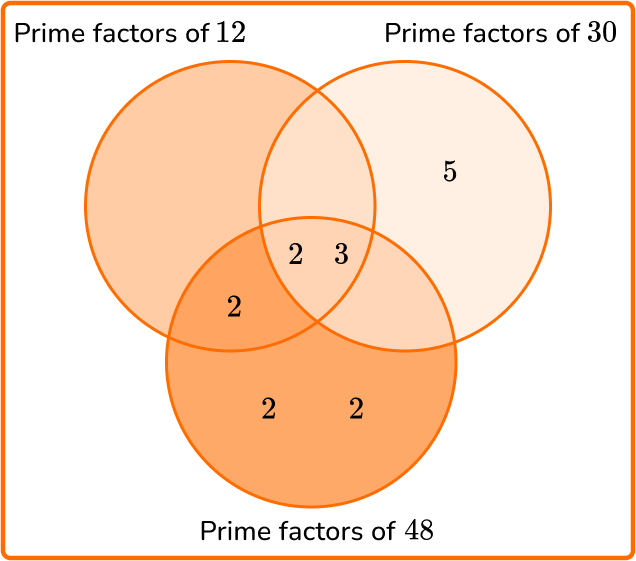
Greatest Common Factor Practice Question 4

GCF $= 2 \times 3=6$

0

1

3

1218

\begin{aligned} &21=3 \times 7\\\\ &58= 2 \times 29 \end{aligned}

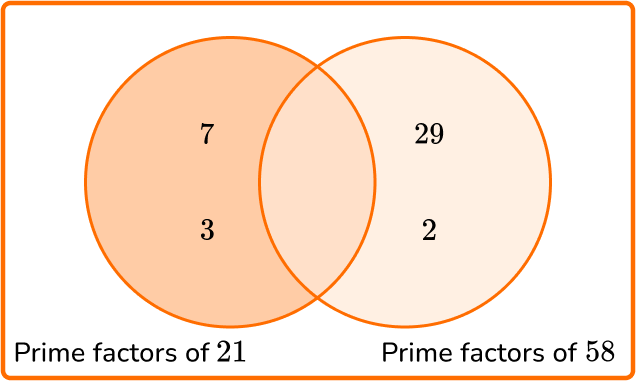
Greatest Common Factor Practice Question 5

All numbers have a factor of $1.$

GCF $= 1$

2

1

4

1,008

Calculate the GCF of $18, 16,$ and $28.$

\begin{aligned} &18=2 \times 3 \times 3\\\\ &16=2 \times 2 \times 2 \times 2\\\\ &28=2 \times 2 \times 7 \end{aligned}

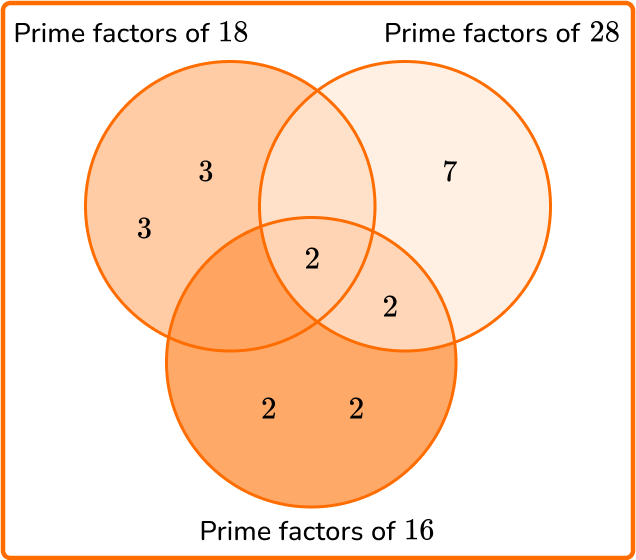
Greatest Common Factor Practice Question 6

GCF $= 2$

Therefore Josh can make $2$ groups of pens with the same number of each color in each group.

Greatest common factor FAQs

Why does the intersection of the Venn diagram contain the GCF?

The intersection contains the greatest common factor because all the shared prime factors are in the intersection. There are no other common prime factors in the set of numbers, otherwise, they would be in the intersection.

Are there other terms for Greatest Common Factor (GCF)?

Greatest Common Divisor (GCD), Greatest Common Denominator (GCD), and Highest Common Factor (HCF) are other terms that mean the same as Greatest Common Factor.

Does the largest number always have more prime factors?

No, not necessarily. For example, the number $24=2 \times 2 \times 2 \times 3$ has $4$ prime factors while $41=41 \times 1$ has only $1,$ so in this case the smallest number has more factors.

Is the greatest factor always the GCF?

No, not necessarily. In order to be the GCF, it has to be a factor of all the given numbers. If it is not a common factor of all the numbers, it is not the GCF.

The next lessons are

Still stuck?

At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.

Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.