Dividing Fractions - Math Steps, Examples & Questions

High Impact Tutoring Built By Math Experts

Personalized standards-aligned one-on-one math tutoring for schools and districts

Request a demo

In order to access this I need to be confident with:

Order of operations Mixed number to improper fraction Improper fraction to mixed number Whole numbers

Math resources Number and quantity Fractions operations

Dividing fractions

Here you’ll learn about dividing fractions including how to divide two fractions, divide fractions by whole numbers, and divide mixed numbers.

Students will first learn about dividing unit fractions in 5th grade math as part of their work in number and operations. They will build on this knowledge and divide all types of fraction in 6th grade math as a part of their work in the number system.

What is dividing fractions?

Dividing fractions occurs when the divisor and/or dividend are fractions or mixed numbers. The concept of dividing fractions is like dividing whole numbers — you are dividing the number into equal shares.

Let’s look at visual representations of dividing by fractions.


$4$ circles divided into two equal groups. Results in two circles per group. $Dividing fractions table image 1$
$2$ circles divided into two equal groups. Results in one circle per group. $Dividing fractions table image 2$
$1$ circles divided into two equal groups. Results in $\cfrac{1}{2} \,$ of circle per group. $Dividing fractions table image 3$

Do you see a pattern between dividing by $2$ and multiplying by $\cfrac{1}{2}?$ They give the same answer.

	Dividing by $\bf{2}$	Multiplying by $\bf{\frac{1}{2}}$
Example $\bf{1}$	$4 \div 2=2$	$4 \times \cfrac{1}{2} = 2$
Example $\bf{2}$	$2 \div 2=1$	$2 \times \cfrac{1}{2} = 1$
Example $\bf{3}$	$1 \div 2= \cfrac{1}{2}$	$1 \times \cfrac{1}{2} = \cfrac{1}{2}$

Let’s look at another visual model.

\cfrac{2}{3} \div \cfrac{1}{2}

in other words, how many $\cfrac{1}{2}$ ’s fit in $\cfrac{2}{3}?$

This will be easier to see if you compare the fractions by finding a common denominator by using equivalent fractions.

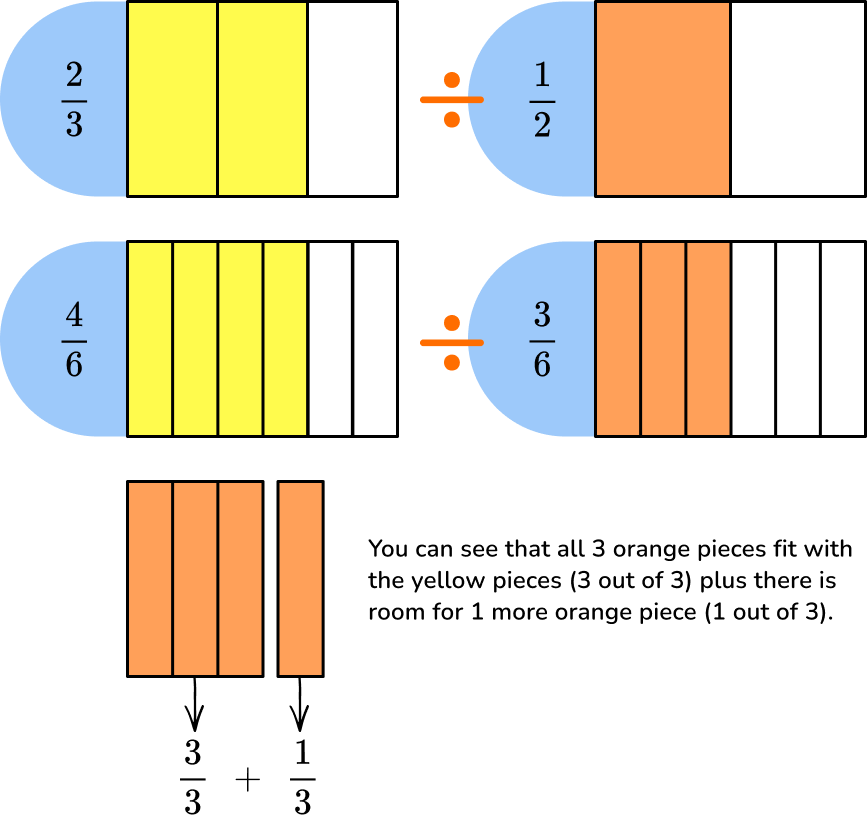
$\cfrac{3}{3}+\cfrac{1}{3}=\cfrac{4}{3}$ pieces fit into the $\cfrac{4}{6}$

So,

$\cfrac{2}{3} \div \cfrac{1}{2}= \cfrac{4}{3} \,$ or $\, 1\cfrac{1}{3}$

We can also apply the rule:

KEEP the first fraction, FLIP the second fraction, CHANGE to multiplication.

\cfrac{2}{3}\div \cfrac{1}{2}

Reciprocal (flip second fraction) $\; \cfrac{1}{2} → \cfrac{2}{1}$

Rewrite to change operation: $\; → \cfrac{2}{3}\times \cfrac{2}{1}$

Multiply: $→ \cfrac{2}{3}\times \cfrac{2}{1} =\cfrac{4}{3}$

Convert back into mixed number $→ \cfrac{4}{3} = 1\cfrac{1}{3}$

What is dividing fractions?

$What is dividing fractions?$

Common Core State Standards

How does this relate to 5th grade math and 6th grade math?

Grade 5 – Number & Operations – Fractions (5.NF.B)
Apply and extend previous understandings of multiplication and division to multiply and divide fractions.

Grade 6 – Number System (6.NS.A)
Apply and extend previous understandings of multiplication and division to divide fractions by fractions.

How to divide fractions

In order to divide fractions:

Take the reciprocal (flip) of the divisor (second fraction).
Change the division sign to a multiplication sign.
Multiply the fractions together.
If possible, simplify or convert to a mixed number.

In order to divide mixed numbers:

Change the mixed number to an improper fraction.
Take the reciprocal (flip) of the divisor (second fraction).
Change the division sign to a multiplication sign.
Multiply the fractions together.
If possible, simplify or convert to a mixed number.

In order to solve dividing fraction word problems:

Create an equation to model the problem
Change any mixed-numbers to an improper fraction.
Take the reciprocal (flip) of the divisor (second fractions).
Change the division sign to a multiplication sign.
Multiply the fractions together.
If possible, simplify or convert to a mixed number.

[FREE] Fraction Operations Check for Understanding Quiz (Grade 4 to 6)

Use this quiz to check your grade 4 to 6 students’ understanding of fraction operations. 10+ questions with answers covering a range of 4th to 6th grade fraction operations topics to identify areas of strength and support!

DOWNLOAD FREE

[FREE] Fraction Operations Check for Understanding Quiz (Grade 4 to 6)

DOWNLOAD FREE

Dividing fractions examples

Example 1: dividing a fraction by a fraction

Divide the numbers $\, \cfrac{1}{2} \div \cfrac{1}{3}.$

Take the reciprocal (flip) of the divisor (second fraction).

$\cfrac{1}{3} → \cfrac{3}{1}$

2Change the division sign to a multiplication sign.

$\cfrac{1}{2} \times \cfrac{3}{1}$

3Multiply the fractions together.

$\cfrac{1}{2} \times \cfrac{3}{1}=\cfrac{3}{2}$

4If possible, simplify or convert to a mixed number.

$\cfrac{3}{2}=1 \cfrac{1}{2}.$

The visual models show the fractions represented with a common denominator. You use equivalent fractions to get the common denominator.

You can see the amount of $\cfrac{1}{3}$ ’s that fit into $\cfrac{1}{2}.$

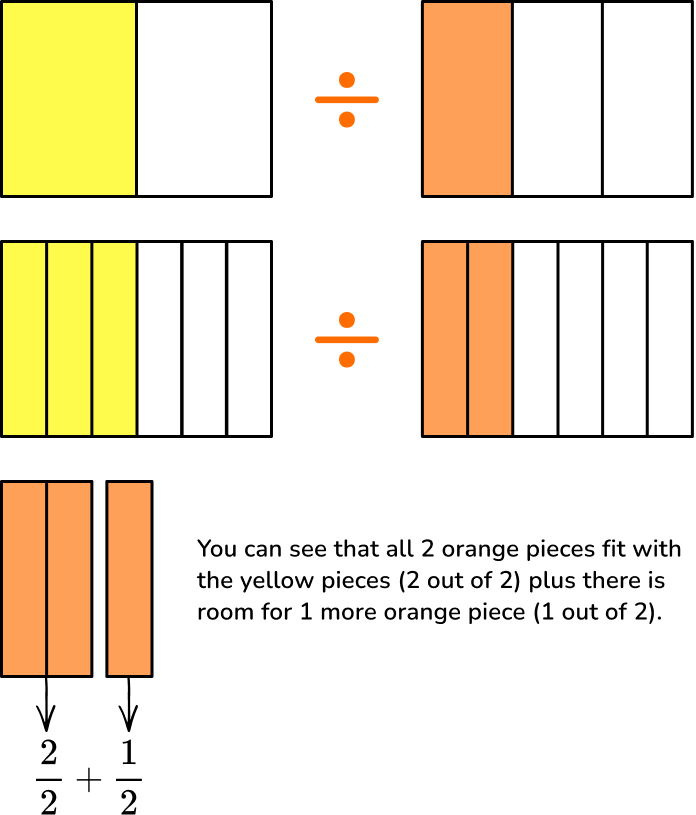
$\cfrac{2}{2} + \cfrac{1}{2}=\cfrac{3}{2} \;$ fit or $\; 1\cfrac{1}{2}$

Example 2: dividing a fraction by a whole number

Divide the numbers $\, \cfrac{1}{2} \div 4.$

Take the reciprocal (flip) of the divisor (second fraction).

$\cfrac{4}{1} → \cfrac{1}{4}$

Change the division sign to the multiplication sign.

$\cfrac{1}{2} \times \cfrac{1}{4}$

Multiply the fractions together.

$\cfrac{1}{2} \times \cfrac{1}{4}=\cfrac{1}{8}$

If possible, simplify or convert to a mixed number.

$\cfrac{1}{8}$ is in its simplest form and cannot be changed into a mixed number.

Example 3: dividing improper fractions

Divide the numbers $\, \cfrac{8}{5} \div \cfrac{4}{3}.$

Take the reciprocal (flip) of the divisor (second fraction).

$\cfrac{4}{3} → \cfrac{3}{4}$

Change the division sign to the multiplication sign.

$\cfrac{8}{5} \times \cfrac{3}{4}$

Multiply the fractions together.

$\cfrac{8}{5} \times \cfrac{3}{4}=\cfrac{24}{20}$

If possible, simplify or convert to a mixed number.

The common factor between the numerator and denominator is $4.$ Using equivalent fractions, the numerator and denominator can both be divided by $4.$

$\cfrac{24 \, \div \, 4}{20 \, \div \, 4}=\cfrac{6}{5}$

$\cfrac{6}{5}$ is in simplest form or it can changed into a mixed number $1\cfrac{1}{5}.$

Example 4: dividing a mixed number by a mixed number

Divide the numbers $\, 1 \cfrac{1}{2} \div 2 \cfrac{1}{4}.$

Change the mixed number to an improper fraction.

$1 \cfrac{1}{2} → \cfrac{3}{2} \;$ and $\; 2 \cfrac{1}{4} → \cfrac{9}{4}$

Take the reciprocal (flip) of the divisor (second fraction).

$\cfrac{9}{4} → \cfrac{4}{9}$

Change the division sign to a multiplication sign.

$\cfrac{3}{2} \times \cfrac{4}{9}$

Multiply the fractions together.

$\cfrac{3}{2} \times \cfrac{4}{9}=\cfrac{12}{18}$

If possible, simplify or convert to a mixed number (mixed fraction).

The common factor of numerator and denominator is $6.$ Using equivalent fractions, the numerator and denominator can both be divided by $6.$

$\cfrac{12 \, \div \, 6}{18 \, \div \, 6} = \cfrac{2}{3}$

$\cfrac{2}{3}$ is in lowest terms.

Example 5: word problem dividing with a whole number

There are $12$ pizzas eaten at a party. Each person ate a quarter of the pizza. How many people ate pizza?

Create an equation to model the problem

$12\div\cfrac{1}{4}= \, ? \;$

Change any mixed-numbers to an improper fraction.

No mixed numbers.

Take the reciprocal (flip) the divisor (second fractions).

$\cfrac{1}{4} → \cfrac{4}{1}$

Change the division sign to a multiplication sign.

$\cfrac{12}{1} \div \cfrac{4}{1}$

Multiply the fractions together.

$\cfrac{12}{1} \div \cfrac{4}{1}=48$

If possible, simplify or convert to a mixed number (mixed fraction).

No simplifying needed

$48$ people

Below is a visual model showing $12$ pizzas divided into quarters. There are $48$ quarters, which means $48$ people were at the party.

Example 6: word problem dividing mixed numbers

If it requires $\cfrac{1}{16}$ of a pound of beef to make a hamburger patty, how many patties can be made with $1\cfrac{1}{8}$ pounds of beef?

Create an equation to model the problem

$1\cfrac{1}{8} \div \cfrac{1}{16}= \, ?$

Change any mixed numbers to an improper fraction.

$1\cfrac{1}{8} → \cfrac{9}{8}$

Take the reciprocal (flip) the divisor (second fractions).

$\cfrac{1}{16} → \cfrac{16}{1}$

Change the division sign to a multiplication sign.

$\cfrac{9}{8} \times \cfrac{16}{1}$

Multiply the fractions together.

$\cfrac{9}{8} \times \cfrac{16}{1}=\cfrac{144}{8}$

If possible, simplify or convert to a mixed number (mixed fraction).

$\cfrac{144}{8}$ has a common factor of $8$ .

$\cfrac{144 \, \div \, 8}{8 \, \div \,8}= \cfrac{18}{1}=18$

$18$ beef patties.

Teaching tips for dividing fractions

Division of fractions is challenging for students to formulate understanding. Utilize hands-on visual models and/or digital models so that students can develop understanding.

Explore patterns so that students can make sense of the steps involved in dividing fractions

Although practicing dividing by fractions is important, do not rely on practice worksheets to develop deep understanding. Using visual models, hands-on activities, and digital games are very effective alternatives to multiplication fractions worksheets.

Although conceptual understanding is essential to learning division of fractions, the simple steps of keep – change – flip help struggling students remember.

Our favorite mistakes

Taking the reciprocal of the dividend (first fraction) instead of the divisor (second fraction)

Not changing the operation to multiplication

Taking the reciprocal of both the dividend and the divisor

After taking the reciprocal of the divisor, cross multiplying the fractions instead of multiplying the fractions

Practice dividing fractions questions

\cfrac{21}{10}

\cfrac{10}{21}

\cfrac{6}{35}

\cfrac{35}{6}

Keep the first fraction $\; \cfrac{2}{7}$

Take the reciprocal (flip) the second fraction $\; \cfrac{3}{5} → \cfrac{5}{3}$

Change division to multiplication $\; \cfrac{2}{7}\times \cfrac{5}{3}$

Multiply $\; \cfrac{2}{7}\times \cfrac{5}{3}= \cfrac{10}{21}$

$\cfrac{10}{21} \;$ is in lowest terms.

\cfrac{60}{21}

\cfrac{35}{9}

\cfrac{9}{35}

\cfrac{6}{21}

\cfrac{6}{7}\div \cfrac{10}{3}

Keep the first fraction $\; \cfrac{6}{7}$

Take the reciprocal (flip) the second fraction $\; \cfrac{10}{3} → \cfrac{3}{10}$

Change division to multiplication $\; \cfrac{6}{7}\times \cfrac{3}{10}$

Multiply the fractions $\; \cfrac{6}{7}\times \cfrac{3}{10}= \cfrac{18}{70}$

$\cfrac{18}{70} \;$ has a common factor of $2.$ Use equivalent fractions to simplify.

\cfrac{18 \, \div \, 2}{70 \, \div \, 2}= \cfrac{9}{35}

$\cfrac{9}{35} \;$ is in lowest terms.

\cfrac{32}{9}

3\cfrac{5}{9}

\cfrac{4}{17}

\cfrac{1}{18}

Keep the first dividend (first fraction) $\; \cfrac{4}{9}$

Take the reciprocal (flip) the divisor (second fraction) $\; 8 → \cfrac{1}{8}$

Change division to multiplication $\; \cfrac{4}{9}\times \cfrac{1}{8}$

Multiply the fractions $\; \cfrac{4}{9}\times \cfrac{1}{8}= \cfrac{4}{72}$

$\cfrac{4}{72} \;$ has a common factor of $4.$ Use equivalent fractions to simplify.

$\cfrac{4 \, \div \, 4}{72 \, \div \, 4}=\cfrac{1}{18} \;$ is in lowest terms.

1\cfrac{13}{20}

4\cfrac{7}{12}

\cfrac{55}{12}

2\cfrac{2}{7}

Change the mixed numbers to improper fractions

2\cfrac{3}{4} → \cfrac{11}{4}

1\cfrac{2}{3} → \cfrac{5}{3}

Keep the dividend (first fraction) $\; \cfrac{11}{4}$

Take the reciprocal (flip) the divisor (second fraction) $\; \cfrac{5}{3} → \cfrac{3}{5}$

Change to multiplication $\; \cfrac{11}{4}\times \cfrac{3}{5}$

Multiply the fractions $\; \cfrac{11}{4}\times \cfrac{3}{5}=\cfrac{33}{20}$

Change back into a mixed number $\cfrac{33}{20} → 1\cfrac{13}{20}$

$3\cfrac{3}{7}$ of the wrap

$1\cfrac{4}{7}$ of the wrap

$\cfrac{7}{11}$ of the wrap

$\cfrac{7}{24}$ of the wrap

Create the equation $\; \cfrac{7}{8}\div {3}= \, ?$

Find the reciprocal (flip) of the divisor (second fraction) $\; 3 → \cfrac{1}{3}$

Change to multiplication $\; \cfrac{7}{8}\times \cfrac{1}{3}$

Multiply the fractions $\; \cfrac{7}{8}\times \cfrac{1}{3}= \cfrac{7}{24}$

$\cfrac{7}{24}$ is in lowest terms.

$\cfrac{7}{24}$ of the gift wrap was used for each package.

$5\cfrac{1}{2}$ pieces of rope

$5\cfrac{1}{8}$ pieces of rope

$3\cfrac{1}{8}$ pieces of rope

$3$ pieces of rope

Create the equation $\; 4\cfrac{1}{8}\div \cfrac{3}{4}= \, ?$

Convert mixed number to improper fractions $\; 4\cfrac{1}{8} → \cfrac{33}{8}$

Take reciprocal (flip) of the second fraction $\; \cfrac{3}{4} → \cfrac{4}{3}$

Change to multiplication $\; \cfrac{33}{8}\times \cfrac{4}{3}$

Multiply together $\; \cfrac{33}{8}\times \cfrac{4}{3}=\cfrac{132}{24}$

Convert to a mixed number $5\cfrac{12}{24}$

The numerator and denominator have a common factor of $12.$ Using equivalent fractions,

\cfrac{12 \, \div \, 12}{24 \, \div \, 12}=\cfrac{1}{2}

5\cfrac{12}{24}=5\cfrac{1}{2}

$5\cfrac{1}{2}$ pieces of rope

Dividing fractions FAQs:

Is dividing fractions the same as multiplying fractions?

No, when you divide fractions, you multiply by the reciprocal of the divisor. When you multiply fractions, you simply multiply the fractions together and do not take the reciprocal of the second fraction.

With division of fractions, do you have to get a common denominator?

No, you do not have to get a common denominator to divide fractions. However, getting a common denominator can be useful when using visual models for the division of fractions.

What other visual models can be used for dividing fractions?

You can use a grid model to divide fractions where the number of columns is the denominator of the dividend and the number of rows is the denominator of the divisor. You shade the number of columns represented by the numerator of the dividend and circle the number of rows represented by the numerator of the divisor. The quotient is the total number of shaded squares over the total number of circled squares.

$\cfrac{1}{4} \div \cfrac{2}{3} = \cfrac{3}{8}$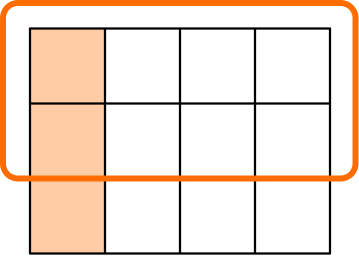

The next lessons are

Still stuck?

At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.

Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.