High Impact Tutoring Built By Math Experts
Personalized standards-aligned one-on-one math tutoring for schools and districts
In order to access this I need to be confident with:
Adding decimals Subtracting decimals Multiplying decimals Dividing decimalsDecimal to fraction
Here you will learn strategies on how to convert decimals to fractions.
Students will first learn about converting decimals to fractions in 4th grade math as part of their work in number and operations with fractions.
What is decimals to fractions?
Converting decimals to fractions is when you represent a decimal as a fraction without changing its value.
Here is a visual model representing 0.43. The hundredths grid is made up of 100 equal parts. 43 pieces are shaded out of 100 equal parts which is \cfrac{43}{100}.
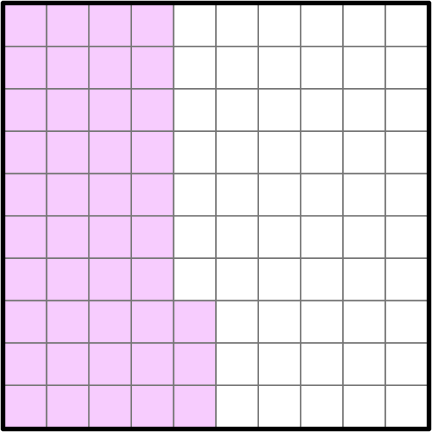
You can also use a place value chart to convert decimals to fractions.
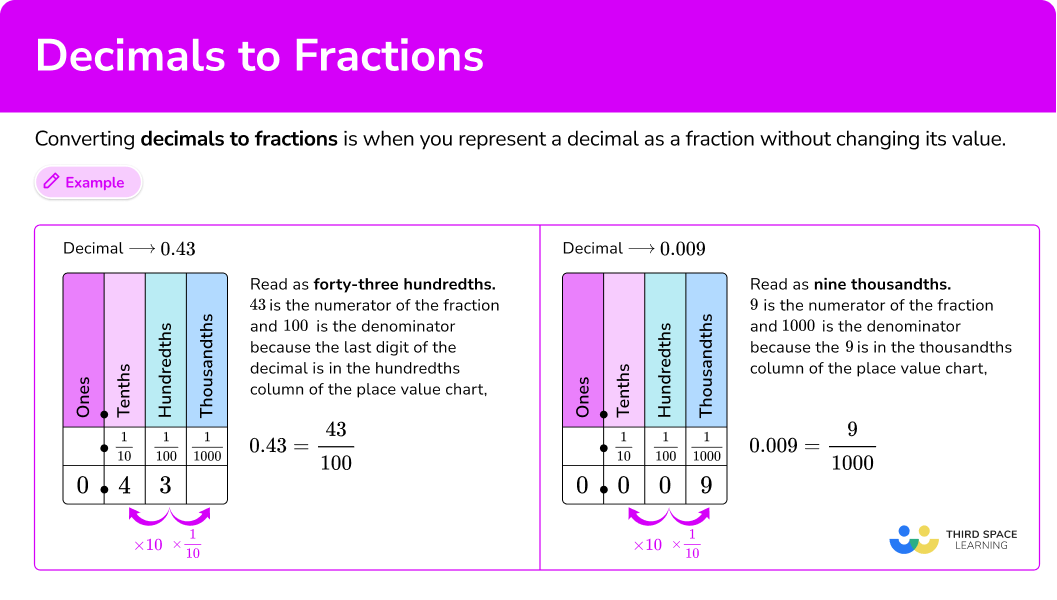
Decimals as fractions \hspace{1cm}
Decimal → 0.43
 Read as forty-three hundredths.
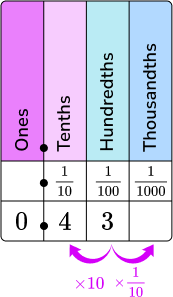
| Decimal → 0.009
 Read as nine thousandths.
|
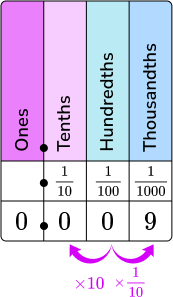
| Decimals as fractions with simplifying |
|---|
Decimal → 0.25  Read as twenty-five hundredths.
|
| Decimals bigger than \bf{1} to a mixed number |
|---|
Decimal → 1.4 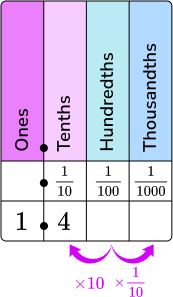 Read as one and four tenths.
|
What is decimals to fractions?
Common Core State Standards
How does this apply to 4th grade math and 5th grade math?
- Grade 4 – Number and Operations – Fractions (4.NF.C.5)
Express a fraction with denominator 10 as an equivalent fraction with denominator 100, and use this technique to add two fractions with respective denominators 10 and 100. For example, express \frac{3}{10} as \frac{30}{100}, and add \frac{3}{10} + \frac{4}{100} = \frac{34}{100}.
- Grade 5 – Number and Operations in Base 10 (5.NBT.A.3)
Read, write, and compare decimals to thousandths.
How to convert decimals to fractions
In order to write a decimal as a fraction with a hundredths chart model:
- Represent the decimal on the hundredths chart.
- The shaded part is the numerator, and the total amount of equal parts is the denominator.
- Write the fraction and simplify if possible.
In order to write a decimal as a fraction:
- Write the decimal in words.
- The numerator is the digits of the decimal, and the denominator is the column of the last digit on the place value chart.
- Write the fraction and simplify if possible.
In order to write a decimal bigger than 1 as a mixed number:
- Write the decimal in words.
- Keep the whole number.
- The numerator is the digits to the right of the decimal point, and the denominator is the column of the last digit in the place value chart.
- Write the mixed number and simplify if possible.
![[FREE] Decimal To Fraction Worksheet (Grade 4 to 5)](https://thirdspacelearning.com/wp-content/uploads/2025/01/Decimal-To-Fraction-Worksheet-listing-image.png)
[FREE] Decimal To Fraction Worksheet (Grade 4 to 5)
![[FREE] Decimal To Fraction Worksheet (Grade 4 to 5)](https://thirdspacelearning.com/wp-content/uploads/2025/01/Decimal-To-Fraction-Worksheet-listing-image.png)
Use this worksheet to check your 4th to 5th grade students’ understanding of decimal to fraction. 15 questions with answers to identify areas of strength and support!
DOWNLOAD FREE![[FREE] Decimal To Fraction Worksheet (Grade 4 to 5)](https://thirdspacelearning.com/wp-content/uploads/2025/01/Decimal-To-Fraction-Worksheet-listing-image.png)
[FREE] Decimal To Fraction Worksheet (Grade 4 to 5)
![[FREE] Decimal To Fraction Worksheet (Grade 4 to 5)](https://thirdspacelearning.com/wp-content/uploads/2025/01/Decimal-To-Fraction-Worksheet-listing-image.png)
Use this worksheet to check your 4th to 5th grade students’ understanding of decimal to fraction. 15 questions with answers to identify areas of strength and support!
DOWNLOAD FREEConvert decimals to fractions examples
Example 1: write a decimal as a fraction using a model
Represent 0.21 as a fraction using a model.
- Represent the decimal on the hundredths chart.
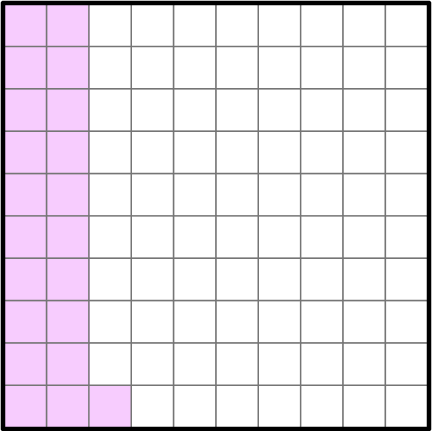
There are 21 parts shaded out of the 100 equal parts.
2The shaded part is the numerator, and the total amount of equal parts is the denominator.
Since there are 21 shaded parts and 100 equal parts. 21 will be the numerator of the fraction, and 100 is the denominator of the fraction.
3Write the fraction and simplify if possible.
0.21 → \cfrac{21}{100}\cfrac{21}{100} \, is in lowest terms.
Example 2: convert a simple decimal to a fraction (without simplifying)
Change 0.3 to a fraction.
Write the decimal in words.
0.3 in words is three-tenths.
The numerator is the digits of the decimal, and the denominator is the column of the last digit on the place value chart.
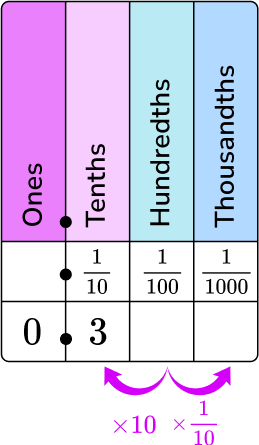
0 is in the ones column, 3 is in the tenths column.
3 will be the numerator and 10 will be the denominator.
Write the fraction and simplify if possible.
\cfrac{3}{10} \, is in lowest terms.
Example 3: convert a decimal to a fraction (with simplifying)
Convert 0.22 to a fraction.
Write the decimal in words.
0.22 in words is twenty-two hundredths.
The numerator is the digits of the decimal, and the denominator is the column of the last digit on the place value chart.
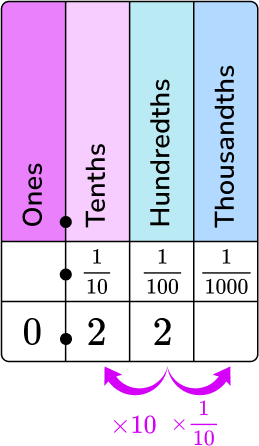
0 is in the ones column, 2 is in the tenths column, and 2 is in the hundredths column.
22 will be the numerator and 100 will be the denominator.
Write the fraction and simplify if possible.
\cfrac{22}{100} \, can be simplified. The common factor between 22 and 100 is 2.
\cfrac{22}{100}=\cfrac{22\div2}{100\div 2}=\cfrac{11}{50}
\cfrac{22}{100} \, in lowest terms is \cfrac{11}{50}.
Example 4: convert a decimal to a fraction involving thousandths
Convert 0.387 to a fraction.
Write the decimal in words.
0.387 in words is three hundred eighty-seven hundredths.
The numerator is the digits of the decimal, and the denominator is the column of the last digit on the place value chart.
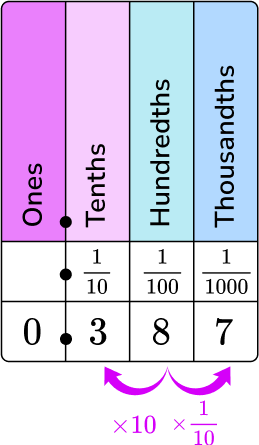
0 is in the ones column, 3 is in the tenths column, 8 is in the hundredths column, and 7 is in the thousandths column.
387 will be the numerator and 1000 will be the denominator.
Write the fraction and simplify if possible.
\cfrac{387}{1000} \, is in lowest terms.
Example 5: convert a decimal bigger than 1 to a mixed number
Convert 1.7 to a mixed number.
Write the decimal in words.
1.7 in words is one and seven tenths.
Keep the whole number.
The whole number will stay at 1.
The numerator is the digits to the right of the decimal point, and the denominator is the column of the last digit in the place value chart.
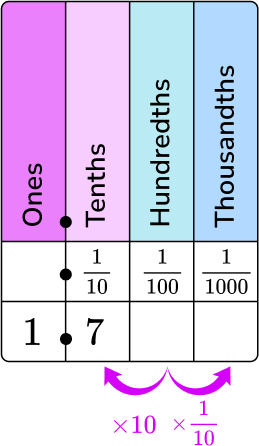
1 is in the ones column, and 7 is in the tenths column.
7 will be the numerator and 10 will be the denominator of the fraction part of the mixed fraction.
Write the mixed number and simplify if possible.
1\cfrac{7}{10} \, is in lowest terms.
Example 6: convert a decimal bigger than 1 to a mixed number (with simplifying)
Convert 2.04 to a fraction.
Write the decimal in words.
2.04 in words is two and four hundredths.
Keep the whole number.
2 will be the whole number.
The numerator is the digits to the right of the decimal point, and the denominator is the column of the last digit in the place value chart.
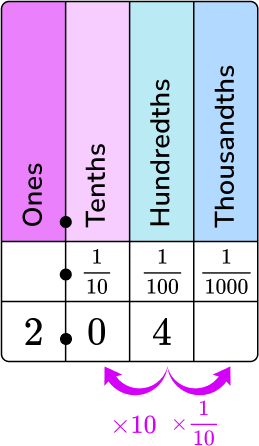
2 is in the ones column, 0 is in the tenths column, and 4 is in the hundredths column.
4 will be the numerator and 100 will be the denominator of the fraction part of the mixed fraction.
Write the mixed number and simplify if possible.
2.04 as mixed number is \, 2\cfrac{4}{100}.
2\cfrac{4}{100} \, can be simplified because 4 is the common factor between 4 and 100.
\cfrac{4 \, \div \, 4}{100 \, \div 4}=\cfrac{1}{25}
2\cfrac{4}{100} \, in lowest terms is 2\cfrac{1}{25}.
Teaching tips for converting decimals to fractions
- Use a visual model to introduce the topic since students should be familiar with how to create a fraction from a model.
- Use a number line to help students formulate number sense with decimal and fraction numbers.
- Reinforcing the decimal value will help students be able to write it in fraction form.
- When teaching the math lessons on converting fractions to decimals, have students change improper fractions to mixed numbers first before making the conversion.
Easy mistakes to make
- Placing the decimal number in the wrong columns on a place value chart
For example, placing the 3 in the decimal number 0.03 in the tenths column instead of the hundredths column.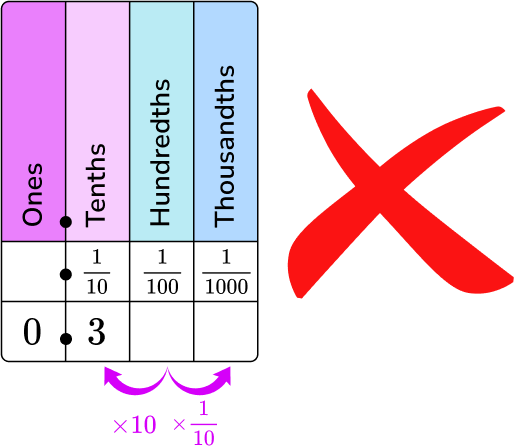
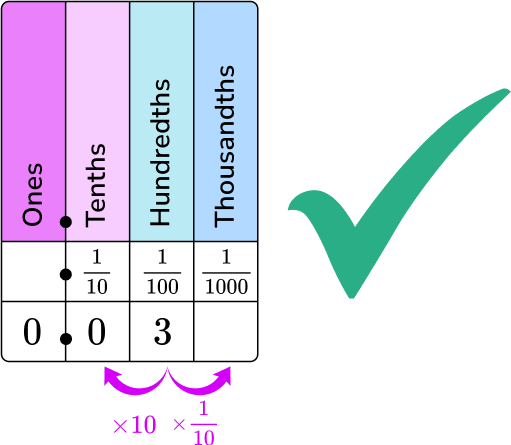
- Forgetting to write the fraction in lowest terms
Always look to see if there is a common factor between the numerator and the denominator of the fraction.
- Confusing the numerator and the denominator
The numerator is the top number, and the denominator is the bottom number.
When converting a decimal to a fraction, the digits of the decimal will be the numerator (top number) and a power of ten will be the denominator (bottom number).
Related lessons on converting fractions, decimals, and percentages
Practice converting decimals to fractions questions
1. Which fraction represents the decimal represented in the model?
0.33
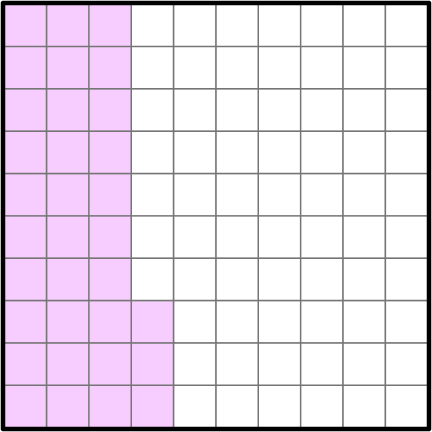




33 shaded parts out of 100 equal parts as a fraction is \, \cfrac{33}{100}.
2. What is 0.1 as a fraction in lowest terms?




0.1 in words is one tenth. Put it on a place value chart.
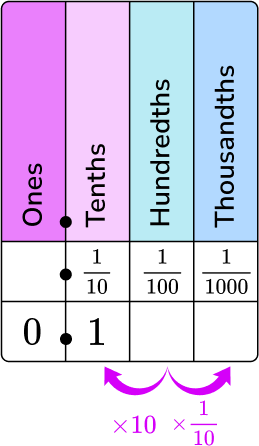
0 is in the ones column and 1 is in the tenths column.
1 will be the numerator, and 10 will be the denominator.
0.1 as a fraction is \, \cfrac{1}{10}.
\cfrac{1}{10} \, is in lowest terms.
3. What is 0.4 as a fraction in lowest terms?




0.4 in words is four tenths. Put it on the place value chart.
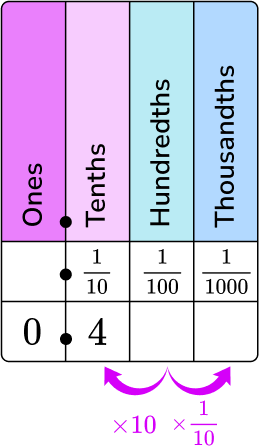
0 is in the ones column and 4 is in the tenths column.
4 will be the numerator, and 10 will be the denominator.
0.4 as a fraction is \, \cfrac{4}{10}.
\cfrac{4}{10} \, can be simplified because the common factor of 4 and 10 is 2.
\cfrac{4 \, \div \, 2}{10 \, \div \, 2}=\cfrac{2}{5}
\cfrac{4}{10} \, in lowest terms is \, \cfrac{2}{5}.
4. What is 0.016 as a fraction in lowest terms?




0.016 in words is sixteen thousandths. Put it on the place value chart.
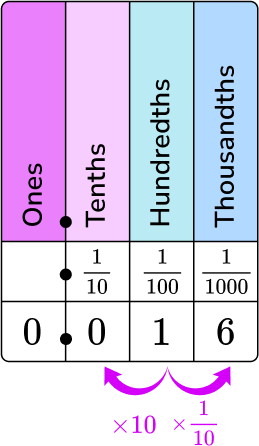
0 is in the ones column, 0 is in the tenths column, 1 is in the hundredths column, and 6 is in the thousandths column.
16 will be the numerator, and 1000 will be the denominator.
0.16 written as fraction is \, \cfrac{16}{1000}.
8 is the common factor between 16 and 1000.
\cfrac{16 \, \div \, 8}{1000 \, \div \, 8}=\cfrac{2}{125}
\cfrac{16}{1000} \, in lowest terms is \, \cfrac{2}{125}.
5. What is 1.23 as a mixed number in lowest terms?




1.23 in words is one and twenty-three hundredths. Put it on the place value chart.
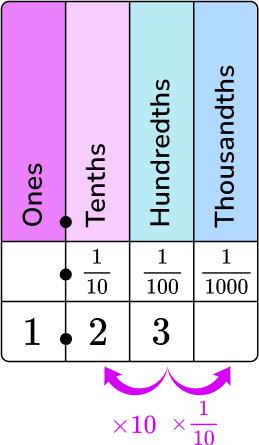
1 is in the ones column, 2 is in the tenths column, and 3 is in the hundredths column.
1 is the whole number part of the mixed number. 23 is the numerator, and 100 is the denominator of the fractional part of the mixed number.
1.23 as a fraction is \, 1\cfrac{23}{100}.
1\cfrac{23}{100} \, is in lowest terms.
6. What is 2.05 as mixed number in its simplest form?




2.05 in words is two and five hundredths. Put it on the place value chart.
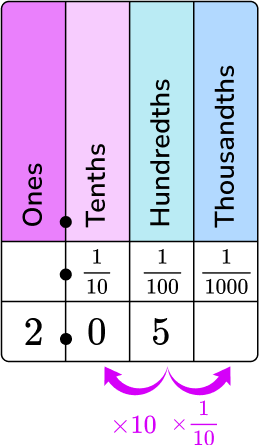
2 is in the ones column, 0 is in the tenths column, and 5 is in the hundredths column.
2 is the whole number part of the mixed number. 5 is the numerator, and 100 is the denominator of the fractional part of the mixed number.
2.05 written as a fraction is \, 2\cfrac{5}{100}.
5 is the common factor between 5 and 100.
\cfrac{5\div 5}{100\div 5}=\cfrac{1}{20}
2\cfrac{5}{100} \, in lowest terms is \, 2\cfrac{1}{20}.
Converting decimals to fractions FAQs
Yes, when converting a decimal to a fraction the denominator of the fraction will always be a power of ten. This is because our decimal system breaks apart the decimal number into tenths (\cfrac{1}{10}), hundredths (\cfrac{1}{100}), thousandths (\cfrac{1}{1000}), etc.
It’s a good practice to always write a fraction in lowest terms, but refer to your state standards for specific guidance.
Yes, you can go from decimal representation to fraction representation and vice versa. For example, to convert \cfrac{9}{10} \, to a decimal, you can put it on the place value chart.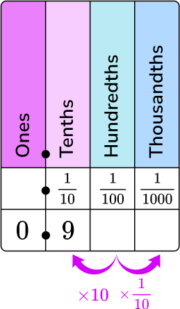
9 will go in the tenths column, so the decimal representation of \cfrac{9}{10} \, is 0.9.
No, there are other ways to convert decimals to fractions. You can use the fraction calculator converter.
A decimal fraction is when the denominator of the fraction is a power of 10. For example, \cfrac{3}{100} \, is a decimal fraction because 100 is 10^2.
Yes, repeating decimals are rational numbers. Rational numbers can be written as fractions. So, repeating decimals can be written as fractions. You will learn how to do this fraction conversion in 8th grade math.
The next lessons are
- Percent
- Compound measures
- Arithmetic
- Properties of equality
- Addition and subtraction
Still stuck?
At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.
Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.

Find out how we can help your students achieve success with our math tutoring programs.
[FREE] Common Core Practice Tests (3rd to 8th Grade)
Prepare for math tests in your state with these 3rd Grade to 8th Grade practice assessments for Common Core and state equivalents.
Get your 6 multiple choice practice tests with detailed answers to support test prep, created by US math teachers for US math teachers!