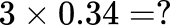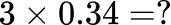[FREE] Fun Math Games & Activities Packs
Always on the lookout for fun math games and activities in the classroom? Try our ready-to-go printable packs for students to complete independently or with a partner!
In order to access this I need to be confident with:
Whole numbers Multiplying multi-digit numbers Distributive propertyMultiplying decimals
Here you will learn about multiplying decimals, including how to multiply decimals by a whole number and multiply decimals by decimals.
Students will first learn about multiplying decimals in 5th grade math as part of their work in number and operations.
What is multiplying decimals?
Multiplying decimals is when you multiply numbers involving decimals.
Let’s look at strategies for multiplying decimal numbers.
| Multiplying Decimal Number By Decimal Number |
|---|
| Modeling with a Hundredths Grid |
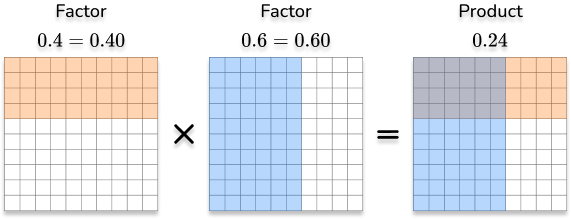   The product is the overlapped shaded area. There are 24 shaded squares in the overlapped area, so the product is \bf{0.24.} |
| Using the Algorithm |
    |
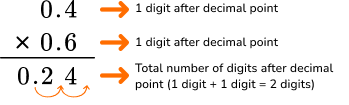| Multiplying A Whole Number By Decimal Number |
|---|
| Modeling with a Hundredths Grid |
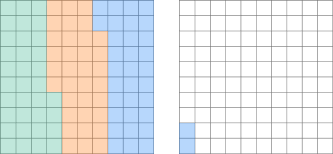    The product is the sum of all the shaded squares, which is 102. The product is \bf{1.02.} |
| Using the Algorithm |
    |
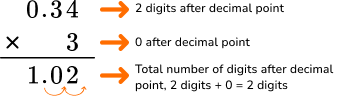What is multiplying decimals?
Common Core State Standards
How does this relate to 5th and 6th grade math?
- Grade 5: Number & Operations Base Ten (5.NBT.B.7)
Add, subtract, multiply, and divide decimals to hundredths, using concrete models or drawings and strategies based on place value, properties of operations, and/or the relationship between addition and subtraction; relate the strategy to a written method and explain the reasoning used.
- Grade 6: The Number System (6.NS.B.3)
Fluently add, subtract, multiply, and divide multi-digit decimals using the standard algorithm for each operation.
![[FREE] Multiplying Decimals Worksheet (Grade 5 to 6)](https://thirdspacelearning.com/wp-content/uploads/2023/12/Multiplying-Decimals-Worksheets-listing-image.png)
[FREE] Multiplying Decimals Worksheet (Grade 5 to 6)
Use this worksheet to check your grade 5 to 6 students’ understanding of multiplying decimals. 15 questions with answers to identify areas of strength and support!
DOWNLOAD FREE [FREE] Multiplying Decimals Worksheet (Grade 5 to 6)
Use this worksheet to check your grade 5 to 6 students’ understanding of multiplying decimals. 15 questions with answers to identify areas of strength and support!
DOWNLOAD FREEHow to multiply decimals
In order to multiply decimals using the standard algorithm.
- Stack the number with the most digits on top.
- Multiply as if the numbers were multi-digit whole numbers, regrouping when necessary.
- Count the number of digits after the decimal point for each factor.
- Put the same number of digits after the decimal point for the product.
In order to solve decimal multiplication word problems.
- Create an equation to model the problem.
- Stack the number with the most digits on top.
- Multiply as if the numbers were multi-digit whole numbers, regrouping when necessary.
- Count the number of digits after the decimal point for each factor.
- Put the same number of digits behind the decimal as the product.
- Label the product.
Multiplying decimal examples
Example 1: multiplying a decimal number by a decimal number
Find the product of 0.8 \times 0.4 .
- Stack the number with the most digits on top.
Both factors have the same number of digits, so it does not matter which one is on top.
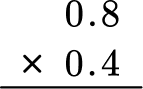
2Multiply as if the numbers were multi-digit whole numbers, regrouping when necessary.
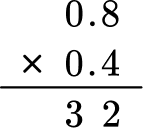
3Count the number of digits after the decimal point for each factor.
Together, there are two numbers after the decimal point.
4Put the same number of digits after the decimal point for the product.
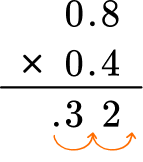
Move the decimal point two decimal places. The product will have two digits after the decimal point.
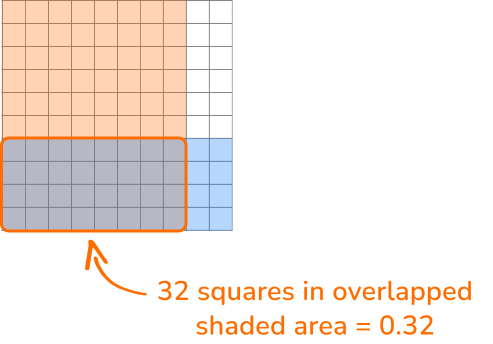
The product is 0.32.
On the hundredths grid, look at the overlapped shaded region. There are 32 squares in that area which is 32 hundredths or 0.32
Example 2: multiplying a decimal number by a whole number
Find the product of 1.21 \times 3 .
Stack the number with the most digits on top.
1.21 has more digits than 3, so 1.21 will be on top.
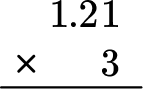
Multiply as if the numbers were multi-digit whole numbers, regrouping when necessary.
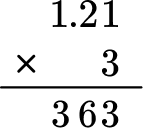
Count the number of digits after the decimal point for each factor.
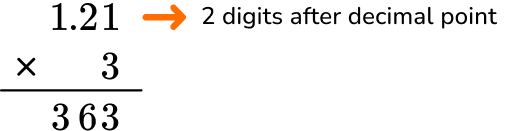
In total, there are two decimal places after the decimal point.
Put the same number of digits behind the decimal for the product.
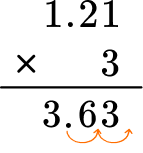
Move the decimal point two decimal places. The product will have two digits after the decimal point.
The product is 3.63
Looking at the hundredths grids, you can see there are 3 groups of 1.21 that represent 363 shade squares, 363 squares = \; 3.63
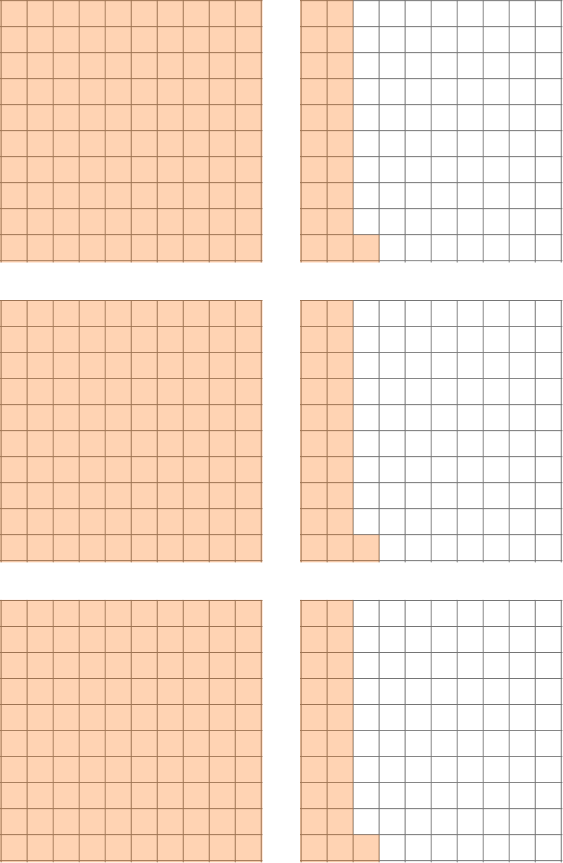
Example 3: multiplying a decimal number by a decimal number
Find the product of 3.4 \times 43.2 .
Stack the number with the most digits on top.
43.2 has more digits than 3.4, so it will go on top.
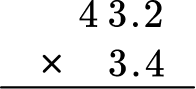
Multiply as if the numbers were multi-digit whole numbers, regrouping when necessary.
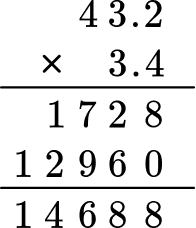
Count the number of digits after the decimal point for each factor.
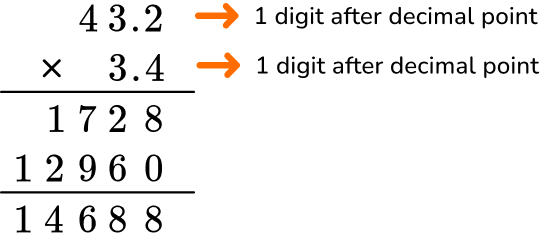
In total, there are two decimal places after the decimal point.
Put the same number of digits behind the decimal for the product.
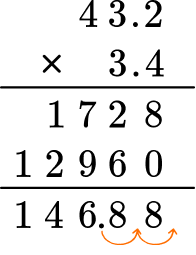
Move the decimal point two decimal places. The product will have two digits after the decimal point.
The product is 146.88
Example 4: multiplying a decimal by a decimal
Solve the multiplication problem, 1.642 \times 32.7 .
Stack the number with the most digits on top.
1.642 has more digits than 32.7, so it will go on top.
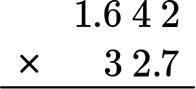
Multiply as if the numbers were multi-digit whole numbers, regrouping when necessary.
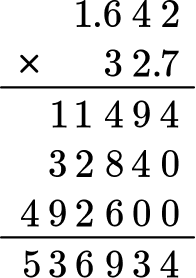
Count the number of digits after the decimal point for each factor.
In total, there are four decimal places after the decimal point.
Put the same number of digits behind the decimal for the product.
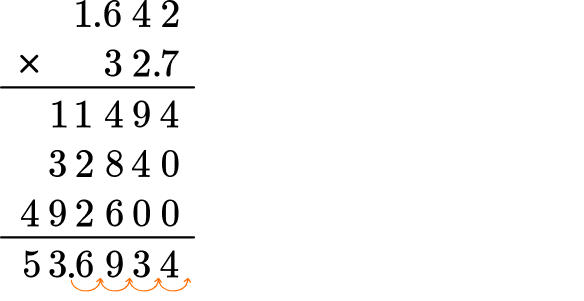
Move the decimal point four decimal places. The answer has four digits after the decimal point.
The product is 53.6934
Example 5: word problem multiplying a whole number by a decimal number
Kit claims she has 4.5 times as many songs on her playlist as Kai. If Kai has 48 songs on his playlist, how many does Kit have on hers?
Create an equation to model the problem
4.5 \times 48 = \; ?
Stack the number with the most digits on top.
48 and 4.5 have the same number of digits. It does not matter which one goes on top.
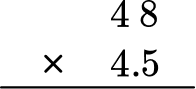
Multiply as if the numbers were multi-digit whole numbers, regrouping when necessary.
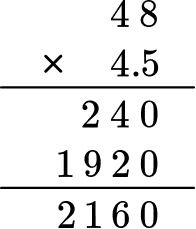
Count the number of digits after the decimal point for each factor.
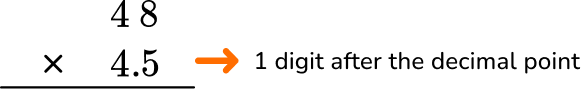
In total, there is one decimal place after the decimal point.
Put the same number of digits behind the decimal for the product.
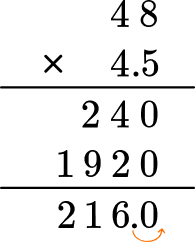
Move the decimal point one decimal place. The product will have one digit after the decimal point.
The product is 216.0 or 216
Label the product.
Kit has 216 songs on her playlist.
Example 6: word problem multiplying decimal number by a decimal number
On Jupiter, objects weigh about 2.4 times as much as they do on Earth. How much would a 9.45 -pound puppy weigh on Jupiter?
Create an equation to model the problem
9.45 \times 2.4 = \; ?
Stack the number with the most digits on top.
9.45 has more digits, so it will go on top.
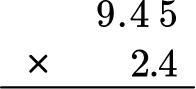
Multiply as if the numbers were multi-digit whole numbers, regrouping when necessary.
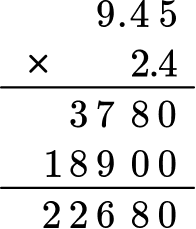
Count the number of digits after the decimal point for each factor.
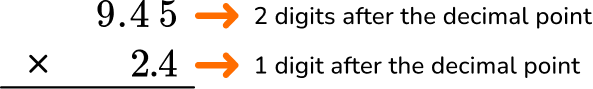
In total, there are three decimal places after the decimal point.
Put the same number of digits behind the decimal for the product.
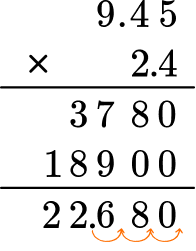
Move the decimal point three decimal places. The product will have three digits after the decimal point.
The product is 22.680 or 22.68
Label the product.
The puppy will weigh 22.68 pounds on Jupiter.
Teaching tips for multiplying decimals
- In 5th grade math, students are first taught about decimal multiplication using visual models such as hundredths grids. As they develop understanding they are able to connect the algorithm of multi-digit multiplication to the multiplication of decimals.
- Explore other strategies for decimal multiplication such as partial products, which emphasize the distributive property and may be easier for students to understand.
- Although practicing the skill of decimal multiplication is important, do not rely on practice worksheets to develop deep understanding. Using visual models, hands-on activities, and digital games are very effective alternatives to multiplication problem worksheets.
Our favorite mistakes
- Placing the decimal point in the wrong position in the answer (product)
It is important to remember to count the number of places that are in both factors. The total number of digits to the right of the decimal point is how many the answer should have to the right of the decimal point.
- Leaving the decimal point out completely
- Thinking that the decimal points of the products need to line up before multiplying like they do in addition of decimals
Practice multiplying decimals questions
1. Find the product of the numbers.
14 \times 4.37 = \; ?
4.37 has more digits than 14, so it will go on top.
In total, there are two decimal places after the decimal point. Move the decimal point two decimal places. The answer will have two digits after the decimal point.
Product = \; 61.18
2. Find the product of the two numbers.
5.21 \times 1.6 = \; ?
5.21 has more digits than 1.6, so it will go on top.
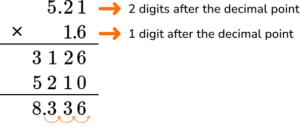
There are a total of three digits after the decimal point. Move the decimal point three decimal places
Product = \; 8.336
3. Find the product of the numbers.
0.264 \times 1.1 = \; ?
0.264 has more digits than 1.1, so it will go on top.
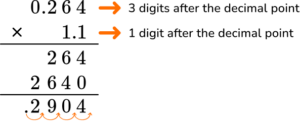
There are a total of four digits after the decimal point. Move the decimal point four decimal places.
Product = \; 0.2904
4. Kaylee went to the bookstore to buy 6 books she needed for her class. If the books cost \$17.25 each, how much did she spend on her books?
If one book costs \$17.25, then six books will cost 6 \times \$17.25.
17.25 has more digits, so it will go on top.
There are a total of two digits after the decimal point. Move the decimal point two decimal places.
Kaylee will spend \$103.25 on the 6 books.
5. The local farmer sold 13.2 pounds of tomatoes. She sold 2.5 times more apples than tomatoes. How many pounds of apples did she sell?
33.3 pounds
33 pounds
3.3 pounds
33.33 pounds
2.5 times more pounds of apples were sold than tomatoes. Multiply 2.5 times 13.2.
13.2 has more digits than 2.5, so it will go on top.
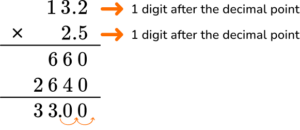
There are a total of two digits after the decimal point. Move the decimal point two decimal places.
33.00 = 33 pounds of apples were sold.
Multiplying decimals FAQs:
No, you can use the strategy that works best for you. For example, you can use partial products to multiply decimals the way you would multi-digit whole numbers.
\bf{1.2} \; \textbf{×} \; \bf{3.4} 
Yes, in 6th grade, you will become very familiar with changing decimals to fractions and fractions to decimals. However, there are certain situations where keeping the number as a decimal might be easier.
Work typically involves multiplying numbers that have values in either the tenths place, hundredths place and/or the thousandths place.
\begin{aligned} & \quad \quad \bf{1.3} \quad \quad \textbf{×} \quad \quad \bf{3.4} \quad \quad \textbf{=} \quad \quad \bf{4.08} \\ & \quad \quad \;\; \text{⇧} \quad \quad \quad \quad \quad \; \text{⇧} \quad \quad \quad \quad \quad \;\; \text{⇧}\\ & \text{multiplicand} \quad \; \text{multiplier} \quad \quad \text{product} \end{aligned}
Still stuck?
At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.
Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.
Find out how we can help your students achieve success with our math tutoring programs.
[FREE] Common Core Practice Tests (Grades 3 to 6)
Prepare for math tests in your state with these Grade 3 to Grade 6 practice assessments for Common Core and state equivalents.
40 multiple choice questions and detailed answers to support test prep, created by US math experts covering a range of topics!