[FREE] Fun Math Games & Activities Packs
Always on the lookout for fun math games and activities in the classroom? Try our ready-to-go printable packs for students to complete independently or with a partner!
Decimal number line
Here you will learn about decimal number lines, including what decimal number lines are and how to use them.
Students will first learn about decimal number lines as part of numbers and operations in base 10 in 5th grade. They will build on this knowledge as part of the number system in 6th grade.
What is a decimal number line?
A decimal number line is a number line that includes decimal increments and can help us to visualize decimal numbers.
Decimals are numbers that have parts that are not whole. They represent values in between whole numbers such as tenths, hundredths, thousandths, and so on.
For example, this number line goes up from 0 to 1 by tenths (0.1).
Below, the number 0.638 has been marked on a decimal number line. Its position has been estimated between 0.6 and 0.7, but closer to 0.6.
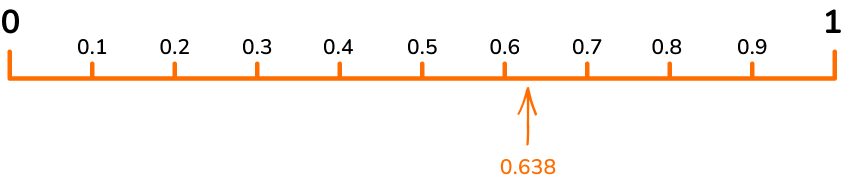
If you zoom in between 0.6 and 0.7 to a number line that goes up by hundredths (0.01), you can position the decimal 0.638 more accurately. This time the position has been estimated between 0.63 and 0.64, but closer to 0.64.
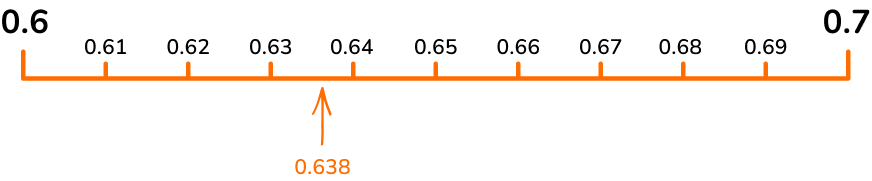
If you zoom in once again between 0.63 and 0.64 to a number line that goes up by thousandths (0.001), then you can place the decimal 0.638 in its exact position.
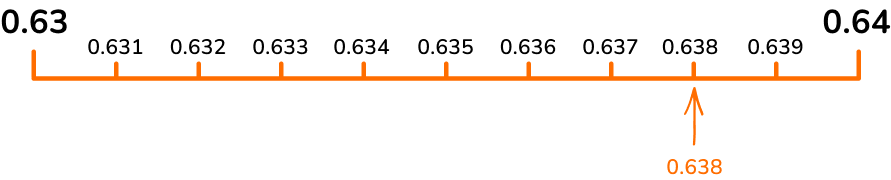
Tenths, hundredths and thousandths are common decimal scales, but they are not the only ones you can use. Decimal number lines can use any decimal scale as long as the intervals are split into equal parts.
For example, this decimal number line goes up from 0 to 1 by two-tenths (0.2).
For example, this decimal number line goes up from 0 to 5 by five-tenths (0.5).
For example, this decimal number line goes up from 0 to 2 by twenty-five hundredths (0.25).
Decimal number lines can also be used to represent negative numbers.
For example, this decimal number line goes up from -3 to 2 by five-tenths (0.5).
What is a decimal number line?
Common Core State Standards
How does this relate to 5th grade math and 6th grade math?
- Grade 5 – Numbers and Operations in Base 10 (5.NBT.A.3)
Read, write, and compare decimals to thousandths.
- Grade 6 – The Number System (6.NS.C.6.3)
Find and position integers and other rational numbers on a horizontal or vertical number line diagram.
How to fill in values on a decimal number line
In order to fill in values on a decimal number line:
- Consider the top and bottom of the scale and the number of intervals.
- Calculate the length of each interval by finding the difference in the top and bottom of the scale and dividing by the number of intervals.
- Fill in the missing values.
![[FREE] Decimal Number Lines Worksheets (Grade 4 to 8)](https://thirdspacelearning.com/wp-content/uploads/2023/12/Decimal-Number-Lines-Worksheets-listing-image.png)
[FREE] Decimal Number Lines Worksheets (Grade 4 to 8)
Use this worksheet to check your grade 4 to 8 students’ understanding of decimal number lines. 15 questions with answers to identify areas of strength and support!
DOWNLOAD FREE [FREE] Decimal Number Lines Worksheets (Grade 4 to 8)
Use this worksheet to check your grade 4 to 8 students’ understanding of decimal number lines. 15 questions with answers to identify areas of strength and support!
DOWNLOAD FREEDecimal number line examples
Example 1: fill in the scale
Fill in the scale.
- Consider the bottom and top of the scale and the number of intervals.
The bottom of the scale is 7, the top of the scale is 8 and there are 5 intervals.
2Calculate the length of each interval by finding the difference in the top and bottom of the scale and dividing by the number of intervals.
To calculate the length of an interval step you can use the formula.
(\text{Top of the scale } - \text{ Bottom of the scale}) \; \div \text{ Number of intervals}This gives,
(8-7)\div 5=0.2So the scale goes up by two-tenths (0.2).
3Fill in the missing values.
Start from 7 and go up the scale, adding 0.2 each time.
Example 2: fill in the scale
Fill in the scale.
Consider the bottom and top of the scale and the number of intervals.
The bottom of the scale is 5, the top of the scale is 9 and there are 8 intervals.
Calculate the length of each interval by finding the difference in the top and bottom of the scale and dividing by the number of intervals.
To calculate the length of an interval step you can use the formula.
(\text{Top of the scale } - \text{ Bottom of the scale}) \; \div \text{ Number of intervals}
This gives,
(9-5)\div 8=0.5
So the scale goes up by five-tenths (0.5).
Fill in the missing values.
Start from 5 and go up the scale, adding 0.5 each time.
Example 3: fill in the scale
Fill in the scale.
Consider the bottom and top of the scale and the number of intervals.
The bottom of the scale is 12, the top of the scale is 14 and there are 5 intervals.
Calculate the length of each interval by finding the difference in the top and bottom of the scale and dividing by the number of intervals.
To calculate the length of an interval step you can use the formula.
(\text{Top of the scale } - \text{ Bottom of the scale}) \; \div \text{ Number of intervals}
This gives,
(14-12)\div 5=0.4
So the scale goes up by four-tenths (0.4).
Fill in the missing values.
Start from 12 and go up the scale, adding 0.4 each time.
Example 4: finding a missing value
Find the missing value.
Consider the bottom and top of the scale and the number of intervals.
The bottom of the scale is 5.2, the top of the scale is 6.0 and there are 8 intervals.
Calculate the length of each interval by finding the difference in the top and bottom of the scale and dividing by the number of intervals.
To calculate the length of an interval step you can use the formula.
(\text{Top of the scale } - \text{ Bottom of the scale}) \; \div \text{ Number of intervals}
This gives,
(6.0-5.2)\div 8=0.1
So the scale goes up by one-tenth (0.1).
Fill in the missing values.
Start from 5.2 and go up the scale, adding 0.1 each time.
The missing value is 5.6.
Example 5: finding a missing value
Find the missing value.
Consider the bottom and top of the scale and the number of intervals.
The bottom of the scale is 14, the top of the scale is 17 and there are 6 intervals.
Calculate the length of each interval by finding the difference in the top and bottom of the scale and dividing by the number of intervals.
To calculate the length of an interval step you can use the formula.
(\text{Top of the scale } - \text{ Bottom of the scale}) \; \div \text{ Number of intervals}
This gives,
(17-14)\div 6=0.5
So the scale goes up by five-tenths (0.5).
Fill in the missing values.
Start from 14 and go up the scale, adding 0.5 each time.
The missing value is 16.5.
Example 6: finding a missing value
Find the missing value.
Consider the bottom and top of the scale and the number of intervals.
The bottom of the scale is 7.1, the top of the scale is 7.5 and there are 8 intervals.
Calculate the length of each interval by finding the difference in the top and bottom of the scale and dividing by the number of intervals.
To calculate the length of an interval step you can use the formula.
(\text{Top of the scale } - \text{ Bottom of the scale}) \; \div \text{ Number of intervals}
This gives,
(7.5-7.1)\div 8=0.05
So the scale goes up by five-hundredths (0.05).
Fill in the missing values.
Start from 7.1 and go up the scale, adding 0.05 each time.
The missing value is 7.45.
Teaching tips for decimal number lines
- Let students spend some time working with blank number lines to create their own representations from scratch. This gives them opportunities to compare and contrast strategies with others and also develop a better understanding of how decimal number lines are created. However, ensure that students understand the importance of creating equal intervals. In fact, it may be beneficial to compare two number lines (one with equal intervals and one without) and have students discuss why decimal number lines are only valid if they have equal intervals.
- Use number line worksheets when applicable, but look for worksheets that show intervals other than tenths or hundredths. Often students see these types in so many activities, that they stop paying attention to the given numbers and intervals – leading to simple mistakes.
- Use real world distance applications of decimal number lines whenever possible. Perhaps there is a rope in the school gym that needs to be measured and labeled at different lengths. Or maybe students can place a piece of masking tape on the floor to create a number line showing the distance from the classroom door to the wall. Using distance in this way allows students to make connections to measurement conversions and ratios and proportions.
- Sixth graders should spend just as much time creating negative decimal number lines as positive decimal number lines.
- To challenge students, have them create a decimal number line that also shows the equivalent fractions and mixed numbers it represents.
Our favorite mistakes
- Assuming a decimal number line goes up in tenths
It is worth double checking what the intervals in a number line are. It is easy to assume it will be tenths, but often other steps are used.
For example,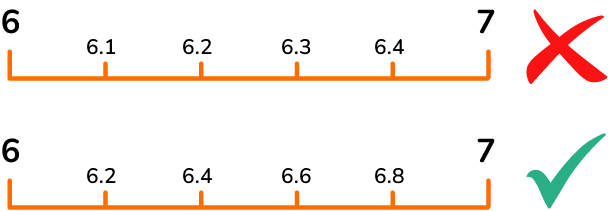
Practice decimal number line questions
1. Find the missing value.
The bottom of the scale is 6, the top of the scale is 7 and there are 5 intervals.
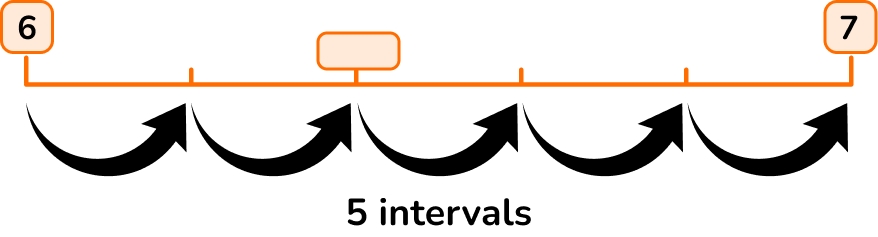
To calculate the length of an interval step you can use the formula:
(\text{Top of the scale } – \text{ Bottom of the scale}) \; \div \text{ Number of intervals}
This gives,
(7-6)\div 5=0.2
Start from 6 and go up the scale, adding 0.2 each time.
The missing value is 6.4.
2. Find the missing value.
The bottom of the scale is 2.1, the top of the scale is 2.7 and there are 6 intervals.
To calculate the length of an interval step you can use the formula:
(\text{Top of the scale } – \text{ Bottom of the scale}) \; \div \text{ Number of intervals}
This gives,
(2.7-2.1)\div 6=0.1
Start from 2.1 and go up the scale, adding 0.1 each time.
The missing value is 2.3.
3. Find the missing value.
The bottom of the scale is 5.2, the top of the scale is 5.3 and there are 10 intervals.
To calculate the length of an interval step you can use the formula:
(\text{Top of the scale } – \text{ Bottom of the scale}) \; \div \text{ Number of intervals}
This gives,
(5.3-5.2)\div 10=0.01
Start from 5.2 and go up the scale, adding 0.01 each time.
The missing value is 5.25.
4. Find the missing value.
The bottom of the scale is 16.2, the top of the scale is 18.2 and there are 5 intervals.
To calculate the length of an interval step you can use the formula:
(\text{Top of the scale } – \text{ Bottom of the scale}) \; \div \text{ Number of intervals}
This gives,
(18.2-16.2)\div 5=0.4
Start from 16.2 and go up the scale, adding 0.4 each time.
The missing value is 17.8.
5. Find the missing value.
The bottom of the scale is 6.5, the top of the scale is 9.0 and there are 10 intervals.
To calculate the length of an interval step you can use the formula:
(\text{Top of the scale } – \text{ Bottom of the scale}) \; \div \text{ Number of intervals}
This gives,
(9.0-6.5)\div 10=0.25
Start from 6.5 and go up the scale, adding 0.25 each time.
The missing value is 7.25.
6. Find the missing value.
The bottom of the scale is 5.5, the top of the scale is 7.3 and there are 6 intervals.
To calculate the length of an interval step you can use the formula:
(\text{Top of the scale } – \text{ Bottom of the scale}) \; \div \text{ Number of intervals}
This gives,
(7.3-5.5)\div 6=0.3
Start from 5.5 and go up the scale, adding 0.3 each time.
The missing value is 6.4.
Decimal number line FAQs
Decimal number lines can help students understand decimal place value and be used to order and compare decimals. They are also helpful as models for adding, subtracting, multiplying or dividing decimals. Students will also use decimal number lines when creating graphs and plotting data.
There is value in having students explore decimal number lines by drawing them themselves. However, there are drawbacks as it can be more time consuming and ensuring that all the intervals are equal can be difficult. For each activity, use discretion to decide whether providing students with premade number lines or letting them create their own is more appropriate for the learning goal.
Still stuck?
At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.
Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.
Find out how we can help your students achieve success with our math tutoring programs.
[FREE] Common Core Practice Tests (Grades 3 to 6)
Prepare for math tests in your state with these Grade 3 to Grade 6 practice assessments for Common Core and state equivalents.
40 multiple choice questions and detailed answers to support test prep, created by US math experts covering a range of topics!