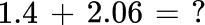High Impact Tutoring Built By Math Experts
Personalized standards-aligned one-on-one math tutoring for schools and districts
In order to access this I need to be confident with:
Addition and subtraction Rounding decimals Place valueAdding decimals
Here you will learn about adding decimals including how to add decimals with models and with the standard algorithm.
Students will first learn about adding decimals as part of numbers and operations in base 10 in 5th grade. They will build on this knowledge and use the standard algorithm to add as a part of the number system in 6th grade.
What is adding decimals?
Adding decimals is when you add numbers involving decimals.
Let’s look at the strategies for adding decimals.
| Adding a decimal number and a decimal number |
|---|
| Modeling with a Hundredths Grid |
 Just like with multi-digit whole numbers, combine each place value.    Then write the answer in standard form:  |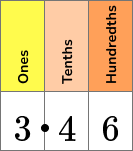
| Using the Algorithm |
 
1. Stack the numbers, lining
up the decimal |
What is adding decimals?
Common Core State Standards
How does this relate to 5th grade math and 6th grade math?
- Grade 5 – Numbers and Operations in Base 10 (5.NBT.B.7)
Add, subtract, multiply, and divide decimals to hundredths, using concrete models or drawings and strategies based on place value, properties of operations, and/or the relationship between addition and subtraction; relate the strategy to a written method and explain the reasoning used.
- Grade 6 – The Number System (6.NS.B.3)
Fluently add, subtract, multiply, and divide multi-digit decimals using the standard algorithm for each operation.
How to add decimals
In order to add decimals with models:
- Show each number using decimal models.
- Combine each place value.
- Write your final answer with the decimal point.
In order to add decimals with the algorithm:
- Stack the numbers and line up the decimal points (and place value).
- Add each column from right to left and regroup the numbers when necessary.
- Write your final answer with the decimal point and check to make sure your answer is reasonable.
![[FREE] Adding Decimals Worksheets (Grade 5 to 6)](https://thirdspacelearning.com/wp-content/uploads/2023/12/Adding-Decimals-Worksheets-listing-image.png)
[FREE] Adding Decimals Worksheets (Grade 5 to 6)
Use this worksheet to check your grade 5 to 6 students’ understanding of adding decimals. 15 questions with answers to identify areas of strength and support!
DOWNLOAD FREE [FREE] Adding Decimals Worksheets (Grade 5 to 6)
Use this worksheet to check your grade 5 to 6 students’ understanding of adding decimals. 15 questions with answers to identify areas of strength and support!
DOWNLOAD FREEAdding decimals examples
Example 1: adding decimals with models
Solve 3.5 + 4.9 = \; ?
- Show each number using decimal models.
2Combine each place value.
3 ones + \; 4 ones = 7 ones
5 tenths + \; 9 tenths = \; 14 tenths
3Write your final answer with the decimal point.
3.5 + 4.9 = 8.4
Example 2: adding decimals with models
Solve 1.12 + 2.3 = \; ?
Show each number using decimal models.
Combine each place value.
1 one + \; 2 ones = \; 3 ones
1 tenth + \; 3 tenths = \; 4 tenths
2 hundredths
Write your final answer with the decimal point.
Example 3: adding numbers with one decimal place
Solve 5.8 + 3.7 = \; ?
Stack the numbers and line up the decimal points (and place value).
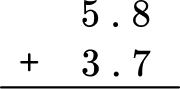
Add each column from right to left and regroup the numbers when necessary.
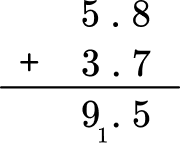
Write your final answer with the decimal point and check to make sure your answer is reasonable.
The answer is 9.5.
Is this answer reasonable? Use rounding to estimate a reasonable answer.
For smaller numbers, you can round to the nearest ones:
5.8 rounds to 6
3.7 rounds to 4
6 + 4 = 10
The sum should be close to 10. Since 9.5 is close, it is a reasonable answer.
Example 4: adding numbers with two decimal places
Solve 9.18 + 7.35 = \; ?
Stack the numbers and line up the decimal points (and place value).
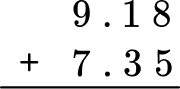
Add each column from right to left and regroup the numbers when necessary.
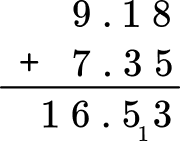
Write your final answer with the decimal point and check to make sure your answer is reasonable.
The answer is 16.53.
Is this answer reasonable? Use rounding to estimate a reasonable answer.
For smaller numbers, you can round to the nearest ones:
9.18 rounds to 9
7.35 rounds to 7
9 + 7 = 16
The sum should be close to 16. Since 16.53 is close, it is a reasonable answer.
Example 5: adding more than two decimal numbers
Solve 3.79 + 2.18 + 14.6 = \; ?
Stack the numbers and line up the decimal points (and place value).
A zero can be added to 14.6 as a placeholder. It does not change the value because 14.6 = 14.60.
Add each column from right to left and regroup the numbers when necessary.
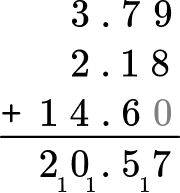
Write your final answer with the decimal point and check to make sure your answer is reasonable.
The answer is 20.57.
Is this answer reasonable? Use rounding to estimate a reasonable answer.
For smaller numbers, you can round to the nearest ones:
3.79 rounds to 4
2.18 rounds to 2
14.6 rounds to 15
4 + 2 + 15 = 21
The sum should be close to 21. Since 20.57 is close, it is a reasonable answer.
Example 6: adding more than two decimal numbers
Solve 34.3 + 22.91 + 56.07 = \; ?
Stack the numbers and line up the decimal points (and place value).
A zero can be added to 34.3 as a placeholder. It does not change the value because 34.3 = 34.30.
Add each column from right to left and regroup the numbers when necessary.
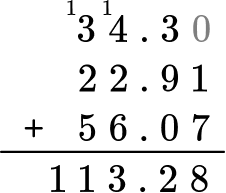
Write your final answer with the decimal point and check to make sure your answer is reasonable.
The answer is 113.28.
Is this answer reasonable? Use rounding to estimate a reasonable answer.
For larger numbers, you can round to the nearest tens:
34.3 rounds to 30
22.91 rounds to 20
56.07 rounds to 60
30 + 20 + 60 = 110
The sum should be close to 110. Since 113.28 is close, it is a reasonable answer.
Teaching tips for adding decimals
- Decimal work in 4th grade centers around understanding through models, particularly area models, number lines and connections to fractions with the denominators 10 and 100. To build on this in 5th grade and 6th grade, always have physical or digital models available for students to use when necessary.
- To introduce this topic, give students a decimal addition problem and give them time to solve in a way that makes sense to them. Then go over the different solving strategies as a whole group.
- In the beginning, you may want to stick to smaller decimals or problems that do not involve regrouping. However, at some point it is important to transition to showing students all kinds of decimal addition problems mixed together. This gives them an opportunity to identify which solving strategy to use.
- Math worksheets may have their place when students are still developing understanding around decimal addition, but once students have a successful strategy and can flexibly operate, incorporate math games or real-life projects that involve addition of decimals.
Our favorite mistakes
- Not lining up the decimal point
A common error when adding decimals occurs when the decimal points are not lined up but instead the last digits are lined up.
For example,
- Forgetting to include the number regrouped
Always add in any numbers that are regrouped. Forgetting to include these values will cause your sum to be incorrect.
Practice adding decimals questions
1. Solve 3.7 + 5.6 = \; ?
Show each number using decimal models.
Then, combine each place value.
3 ones + \; 5 ones = \; 8 ones
7 tenths + \; 6 tenths = \; 13 tenths
Write your final answer with a decimal point.
3.7 + 5.6 = 9.3
You can also solve with the algorithm by lining up the decimal points and adding each column.
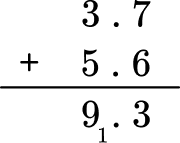
2. Solve 2.84 + 6.19 = \; ?
Show each number using decimal models.
Then, combine each place value.
2 ones + \; 6 ones = \; 8 ones
84 hundredths + \; 19 hundredths = \; 103 hundredths
Write your final answer with the decimal point.
2.84 + 6.19 = 9.03
You can also solve with the algorithm by lining up the decimal points and adding each column.
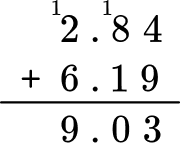
3. Solve 0.069 + 5.987 = \; ?
You can solve with the algorithm by lining up the decimal points and adding each column. Regroup the numbers when necessary.
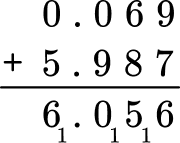
Is this answer reasonable? Use rounding to estimate a reasonable answer. For smaller numbers, you can round to the nearest tenths:
0.069 rounds to 0.1
5.987 rounds to 6
6 + 0.1 = 6.1
The sum should be close to 6.1. Since 6.056 is close, it is a reasonable answer.
4. Solve 2.1 + 3.87 = \; ?
You can solve with the algorithm by lining up the decimal points and adding each column.
A zero can be added to 2.1 as a placeholder. It does not change the value because 2.1 = 2.10.
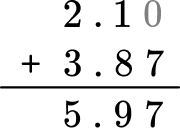
Is this answer reasonable? Use rounding to estimate a reasonable answer. For smaller numbers, you can round to the nearest ones:
2.1 rounds to 2
3.87 rounds to 4
2 + 4 = 6
The sum should be close to 6. Since 5.97 is close, it is a reasonable answer.
5. Solve 9.04 + 17.381 = \; ?
You can solve with the algorithm by lining up the decimal points and adding each column. Regroup the numbers when necessary.
A zero can be added to 9.04 as a placeholder. It does not change the value because 9.04 = 9.040.
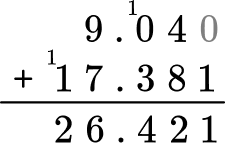
Is this answer reasonable? Use rounding to estimate a reasonable answer. For smaller numbers, you can round to the nearest ones:
9.04 rounds to 9
17.381 rounds to 17
9 + 17 = 26
The sum should be close to 26. Since 26.421 is close, it is a reasonable answer.
6. Solve 20.3 + 13.67 + 0.998 = \; ?
You can solve with the algorithm by lining up the decimal points and adding each column. Regroup the numbers when necessary.
Zeros can be added to 20.3 and 13.67 as placeholders. It does not change the value because 20.3 = 20.300 and 13.67 = 13.670.
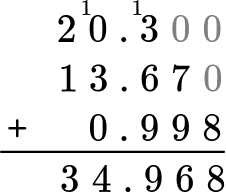
Is this answer reasonable? Use rounding to estimate a reasonable answer. For smaller numbers, you can round to the nearest ones:
20.3 rounds to 20
13.67 rounds to 14
0.998 rounds to 1
20 + 14 + 1 = 35
The sum should be close to 35. Since 34.968 is close, it is a reasonable answer.
Adding decimals FAQs
Yes, you follow the same steps to subtract decimals. The only difference is that you subtract each place value position instead of adding.
No, these strategies will also work when adding whole numbers and numbers with decimals.
Following the Common Core recommendations, in 5th grade, students should work with tenths place, hundredths place and thousandths place. In 6th grade this is expanded to smaller numbers. Check your state’s specific standards for further clarification.
The next lessons are
Still stuck?
At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.
Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.
Find out how we can help your students achieve success with our math tutoring programs.
[FREE] Common Core Practice Tests (3rd to 8th Grade)
Prepare for math tests in your state with these 3rd Grade to 8th Grade practice assessments for Common Core and state equivalents.
Get your 6 multiple choice practice tests with detailed answers to support test prep, created by US math teachers for US math teachers!