Rounding decimals

Here you will learn about rounding decimals, including how to round to the nearest whole number, tenth, and hundredth.

Students will first learn about rounding decimals as part of number and operations in base 10 in 5th grade.

What is rounding decimals?

Rounding decimals involves making a decimal simpler by shortening it to a given number of decimal places. Rounding decimals is a type of estimation used to make calculations easier.

To round decimals, you can use a number line or you can apply a rule.

The rule says that if the digit to the right of the rounding digit is greater than or equal to 5 (such as, 5, 6, 7, 8, 9 ), round up by adding one to the rounding digit. However, when the digit to the right of the rounding digit is less than 5 , leave the rounding digit alone.

For example,

Round \bf{7\underline{8}.6} to the nearest whole number with a number line
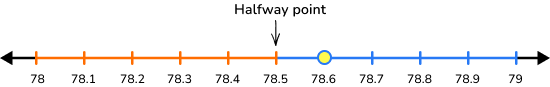78.6 is 0.6 from 78 and 0.4 from 79. It is closer to 79, so it rounds to 79.
Round \bf{7\underline{8}.6} to the nearest whole number with the rule
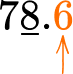8 is in the rounding place, and 6 is to the right of the rounding digit. The rule says that if the number to the right of the rounding digit is greater than or equal to 5 \, (5, 6, 7, 8, 9), round up by adding one to the rounding digit. 6 is greater than 5 , so add 1 to 8, and 8 becomes 9. 7\underline{8}.6 → the nearest whole number is 79

Round \bf{1.\underline{6}1} to the nearest tenth with a number line
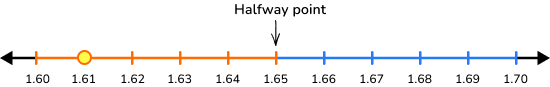1.61 is 0.1 from 1.60 and 0.9 from 1.70. It is closer to 1.60, so it rounds to 1.6 .
Round \bf{1.\underline{6}1} to the nearest whole number with the rule
6 is in the rounding place, and 1 is to the right of the rounding digit. The rule says that if the number to the right of the rounding digit is greater than or equal to 5 \, (5, 6, 7, 8, 9), round up by adding one to the rounding digit. 1 is less than 5 , so leave the rounding digit the same. 1.\underline{6}1 → Rounded to the nearest tenth is 1.6

What is rounding decimals?

Common Core State Standards

How does this relate to 5th grade math?

• Grade 5 – Number and Operations in Base 10 (5.NBT.A.4)
  Use place value understanding to round decimals to any place.

How to round decimals

In order to round decimals with a number line:

1. Create a number line with a scale one position smaller than the rounding number.
2. Count to see if the number being rounded is closer to the number rounded down or up.

In order to round decimals with the rule:

1. Find the rounding place and look at the digit immediately to the right of the rounding place.
2. When that digit is 5 or greater, add 1 to the rounding digit. When it is less than 5, leave the rounding digit alone.
3. Drop all the digits to the right of the rounded digit.
4. Write the rounded number.

Rounding decimals examples

Example 1: rounding to the nearest whole number with a number line

Round 2,340.81 to the nearest whole number.

1. Create a number line with a scale one position smaller than the rounding number.

2,340.81 is being rounded to the nearest whole number, so the number line shows tenths.

Since 2,340.81 is 0.01 larger than 0.8, it is a little to the right of 2,304.8.

2Count to see if the number being rounded is closer to the number rounded down or up.

2,340.81 is a little less than 0.2 from 2,341.0.

2,340.81 rounded to the nearest whole number is 2,341.

**Note: Rounding decimal numbers does not mean that the answer will always have a decimal point. Notice, when rounding to the nearest whole number, a decimal point is not required.

Example 2: rounding to the nearest tenth with a number line

Round 3.47 to the nearest tenth.

Create a number line with a scale one position smaller than the rounding number.

3.47 is being rounded to the nearest tenth, so the number line shows hundredths.

Count to see if the number being rounded is closer to the number rounded down or up.

3.47 is 0.3 away from 3.50.

3.47 rounded to the nearest tenth is 3.5.

Example 3: rounding to the nearest hundredth with a number line

Round 0.176 to the nearest hundredth.

Create a number line with a scale one position smaller than the rounding number.

0.176 is being rounded to the nearest hundredth, so the number line shows thousandths.

Count to see if the number being rounded is closer to the number rounded down or up.

0.176 is 0.04 away from 0.180.

0.176 rounded to the nearest hundredth is 0.18.

Example 4: rounding to the nearest whole number with the rule

Round 33.91 to the nearest whole number.

Example 5: rounding to the nearest tenth with the rule

Round 2.22 to the nearest tenth.

Example 6: rounding to the nearest hundredth with the rule

Round 0.075 to the nearest hundredth.

Teaching tips for rounding decimals

• When teaching students how to round decimals, start with number lines and do not rush through this phase to get to the rule. The rule begins to make sense naturally, once students spend time seeing it play out on a number line. Rushing to the rule too quickly can lead to misconceptions and mistakes later because students will not understand why the rule works.

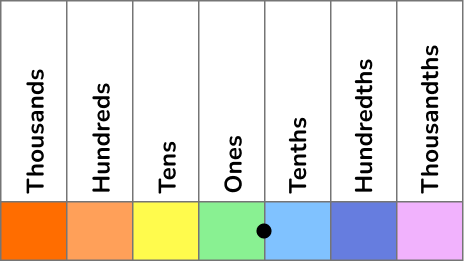
• In order for students to round successfully, they must be proficient in decimal place value. It may be helpful to provide a place value chart as a visual support.
  

Our favorite mistakes

• Decreasing the value of the rounding digit when rounding down
  When rounding down, the value of the rounding digit stays the same, it doesn’t decrease.
  For example, Round 4.62 to the nearest tenth. The 2 tells us to round down, so the rounding number stays the same – it does not go down.
  
  

  

• Getting confused with the place value
  In order to round correctly, students must understand decimal place value or they will confuse the positions when rounding.
  For example, Round 4.51 to the nearest tenth.
  
  

  

• Incorrectly rounding when 9 is in the rounding digit
  When 9 is the rounding digit and it is rounded up, two place value positions change, instead of just one.
  For example, Round 3.497 to the nearest hundredth.
  
  

  

Related rounding numbers lessons

• Rounding numbers
• Place value
• Significant figures
• Estimation

The next lessons are

• Factors and multiples
• Fractions
• Fractions operations

Still stuck?

At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.

Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.

Find out how we can help your students achieve success with our math tutoring programs.