High Impact Tutoring Built By Math Experts
Personalized standards-aligned one-on-one math tutoring for schools and districts
In order to access this I need to be confident with:
Arithmetic Properties of equality Multiplication and divisionMultiplicative comparison
Here you will learn about what multiplicative comparisons are and how to use them to solve word problems.
Students will first learn about multiplicative comparisons in 4th grade and expand that knowledge through 5th grade when working with comparison statements and in 6th grade when learning about ratios.
What is multiplicative comparison?
A multiplicative comparison is a way of comparing two quantities by asking how many times larger or smaller one quantity is than the other quantity.
For example, Mary has twice as many cookies as Tim. Tim has 4 cookies. Mary has twice as many balloons as Tim so the number of cookies Mary has = 2 × 4 = 8.
Multiplicative comparisons involve the operations of multiplication and division to solve problems.
A model can help solve multiplicative comparison problems because it helps you to visualize the amounts that need to be compared and to find the unknown quantity.
Let’s look at a few more examples.
Example 1:
Lucas and Ryan are working on a construction project for school. Lucas’s wood board is 5 times the length of Ryan’s board. If Ryan’s wooden board is 3 feet, how long is Lucas’s wooden board?
Draw a bar model to help visualize the situation.

Ryan has a 3 foot board.
From the model, you can see that Lucas’s board is 5 times the length of Ryan’s board. There are 5 groups of 3 feet.
So the equation is 5 \times 3=\text{ length of Lucas's board}
5 \times 3=15
Lucas’s board is 15 feet.
Example 2:
Mike has 3 lollipops. Michelle has 4 times as many lollipops as Mike. How many lollipops does Michelle have?
Draw a picture to model this situation.
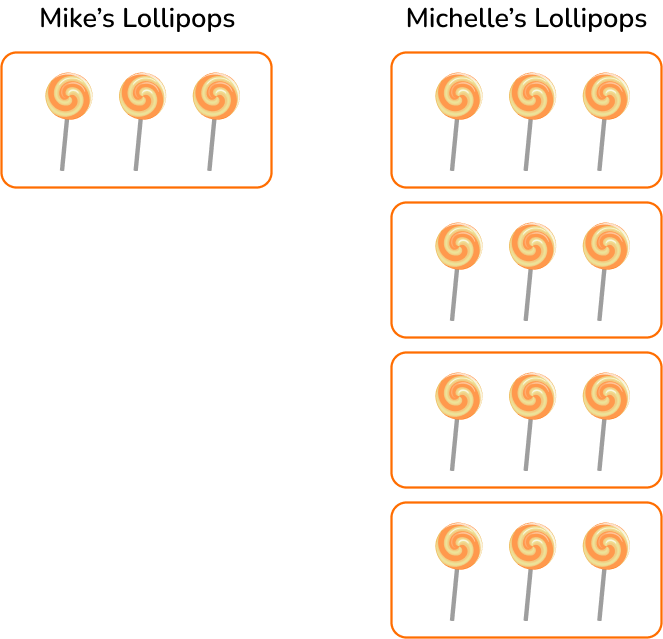
Michelle has four times as many lollipops as Mike. So she has 4 groups of 3 lollipops.
The equation is 4 \times 3=\text { amount of lollipops}
4 \times 3=12
Michelle has 12 lollipops.
Example 3:
Jillian has 12 inches of hair ribbon. Suzanne has half that length. How long is Suzanne’s hair ribbon?
Draw a bar model.

The equation is, \cfrac{1}{2} \, \times 12=\text { length of Suzanne's ribbon}
OR
12 \div 2 = \text { length of Suzanne's ribbon}
12 \div 2=6
Suzanne’s ribbon is 6 inches long.
What is multiplicative comparison?

Common Core State Standards
How does this apply to 4th grade math and 5th grade math?
- Grade 4 – Operations and Algebraic Thinking (4.OA.A.1)
Interpret a multiplication equation as a comparison, for example, interpret 35 = 5 \times 7 as a statement that 35 is 5 times as many as 7 and 7 times as many as 5. Represent verbal statements of multiplicative comparisons as multiplication equations.
- Grade 4 – Operations and Algebraic Thinking (4.OA.A.2)
Multiply or divide to solve word problems involving multiplicative comparison, for example, by using drawings and equations with a symbol for the unknown number to represent the problem, distinguishing multiplicative comparison from additive comparison.
- Grade 5 – Number and Operations Base Ten – (5.NBT.B.7)
Add, subtract, multiply, and divide decimals to hundredths, using concrete models or drawings and strategies based on place value, properties of operations, and/or the relationship between addition and subtraction; relate the strategy to a written method and explain the reasoning used.
![[FREE] Multiplicative Comparison Worksheet (Grade 4)](https://thirdspacelearning.com/wp-content/uploads/2024/04/Multiplicative-Comparison-Worksheet-listing-image.png)
[FREE] Multiplicative Comparison Worksheet (Grade 4)
![[FREE] Multiplicative Comparison Worksheet (Grade 4)](https://thirdspacelearning.com/wp-content/uploads/2024/04/Multiplicative-Comparison-Worksheet-listing-image.png)
Use this worksheet to check your 4th grade students’ understanding of multiplicative comparisons. 15 questions with answers to identify areas of strength and support!
DOWNLOAD FREE![[FREE] Multiplicative Comparison Worksheet (Grade 4)](https://thirdspacelearning.com/wp-content/uploads/2024/04/Multiplicative-Comparison-Worksheet-listing-image.png)
[FREE] Multiplicative Comparison Worksheet (Grade 4)
![[FREE] Multiplicative Comparison Worksheet (Grade 4)](https://thirdspacelearning.com/wp-content/uploads/2024/04/Multiplicative-Comparison-Worksheet-listing-image.png)
Use this worksheet to check your 4th grade students’ understanding of multiplicative comparisons. 15 questions with answers to identify areas of strength and support!
DOWNLOAD FREEHow to solve multiplicative comparison problems
In order to solve multiplicative comparison problems:
- Draw a model.
- Use multiplication or division to write an equation.
- Solve the equation.
Multiplicative comparison examples
Example 1: multiplicative comparison using a bar model with whole numbers
Maddie has collected 21 stickers. Her friend, Anna, has collected 3 times that amount. How many stickers does Anna have in her collection?
- Draw a model.
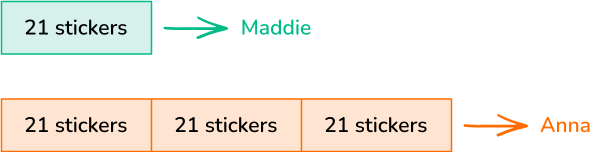
Anna has 3 times the amount of stickers as Maddie. So she has 3 groups of 21.
2Use multiplication or division to write an equation.
The equation is 3 \times 21= \; ?
3State the answer.
3 \times 21=63
Anna has 63 stickers.
Example 2: multiplicative comparison using a bar model with whole numbers
Aderonke owns an animal shelter. She has 24 dogs in her shelter and twice as many cats. How many cats are in the shelter?
Draw a model.
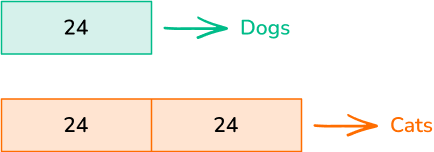
There are twice as many cats as dogs which means there are two groups of 24.
Use multiplication or division to write an equation.
The equation is 2 \times 24= \; ?
Solve the equation.
2 \times 24=48
Aderonke has 48 cats in her animal shelter.
Example 3: multiplicative comparison using a bar model
Amani has 18 yards of wire. Austin has a third of that length of wire. How much wire does Austin have?
Draw a model.

Austin’s wire is a third of the length of Amani’s wire. So, 18 yards is divided into three equal groups.
Use multiplication or division to write an equation.
The equation is 18 \div 3=\text{ length of Austin's wire}
OR
\cfrac{1}{3} \times 18=\text { length of Austin's wire}
Solve the equation.
\begin{aligned} & 18 \div 3=6 \\\\ & \cfrac{1}{3} \, \times 18=\cfrac{18}{3} \, =6 \end{aligned}
Austin’s wire is 6 yards long.
Example 4: multiplicative comparison using a bar model
Billy saved \$122 dollars. His sister, Nikki, has saved 4 times that amount. How much money has Nikki saved?
Draw a model.

Nikki has 4 times the amount of money saved than Billy, which means she has 4 groups of \$122.
Use multiplication or division to write an equation.
The equation is 4 \times 122=\text{ amount of money Nikki saved}
Solve the equation.
4 \times 122=488
Nikki saved \$488.
Example 5: multiplicative comparison with decimals
Jerome’s neighbor has 92 yards of fencing. Jerome has a fourth of that amount of fencing. How much fencing does Jerome have?
Draw a model.

Jerome’s neighbor has 92.4 feet of fencing. He has a fourth of that amount, which means 92.4 is divided into 4 equal groups.
Use multiplication or division to write an equation.
The equation is 92.4 \div 4=\text { length of Jerome's fence}
Solve the equation.
92.4 \div 4=23.1
Jerome has 23.1 yards of fencing.
Example 6: multiplicative comparison with fractions
Carl has 5 \, \cfrac{1}{2} \, gallons of paint. Lucy has three times that amount.
How many gallons of paint does Lucy have?
Draw a model.
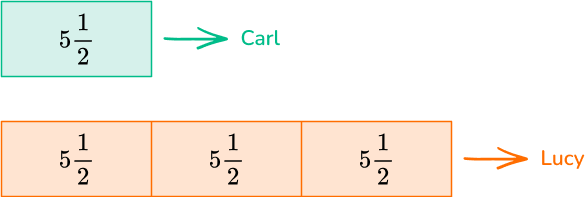
Lucy has three times the amount of gallons of paint than Carl which means there are 3 groups of 5 \, \cfrac{1}{2} .
Use multiplication or division to write an equation.
The equation is 3 \times 5 \cfrac{1}{2}=\text { gallons of paint for Lucy}
Solve the equation.
\begin{aligned} & 3 \times 5 \, \cfrac{1}{2} \, =3 \times \cfrac{11}{2} \\\\ & 3 \times \cfrac{11}{2} \, =\cfrac{33}{2} \, =16 \cfrac{1}{2} \end{aligned}
Lucy has 16 \, \cfrac{1}{2} \, gallons of paint.
Teaching tips for multiplicative comparison
- Connect visual models to the equations so students can see the visual representation of the abstract equation.
- Math worksheets have their place in a math lesson, but providing students with alternative opportunities to practice such as math games or digital platforms are more engaging.
- Another visual representation that can be used when doing multiplicative comparison word problems is the number line.
- Incorporate projects such as having students create their own multiplicative comparison word problems with answer keys and share them on the Google Classroom.
Easy mistakes to make
- Confusing when to use multiplication versus when to use division
For example, when you are given an amount such as 18 and are asked to find 3 times that amount, use multiplication. However, if you are given the amount of 18 and are asked to find a third of that amount, use division.
Related multiplication and division lessons
Practice multiplicative comparison problems
1. Doug has 16 pieces of candy. Dhalia has 3 times that amount. How many pieces of candy does Dhalia have?




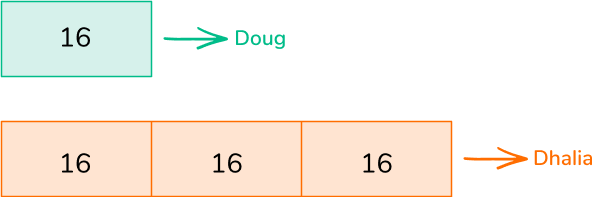
Dhalia has 3 times the amount of candy as Doug which means she has 3 groups of 16.
3 \times 16=48
Dhalia has 48 pieces of candy.
2. Danni has 35 pens in her classroom. Jo has 5 times that amount. How many pens does Jo have in her classroom?




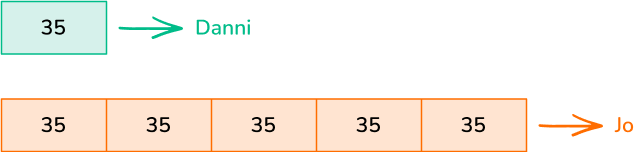
Jo has 5 times as many pens as Danni which means she has 5 groups of 35.
5\times 35=175
Jo has 175 pens in her classroom.
3. Coach Tony has 82 students trying out for his volleyball team. Coach Luke has half that amount trying out for his soccer team. Which equation represents the amount of students trying out for Coach Luke’s soccer team?





Coach Luke has half the number of students trying out for his soccer team than Coach Tony which means 82 is divided into 2 equal groups.
82 \div 2=41
4. Devin has \$243.30 in her savings account. Debra has a third of that amount in her savings account. How much money does Debra have?





Debra has a third of the amount of money as Devin. So \$243.30 has to be divided into 3 equal groups.
243.30 \div 3=81.10
Debra has \$81.10 .
5. Julie has 4 \, \cfrac{2}{3} \, feet of yarn. Dylan has 6 times that amount. How much yarn does Dylan have?




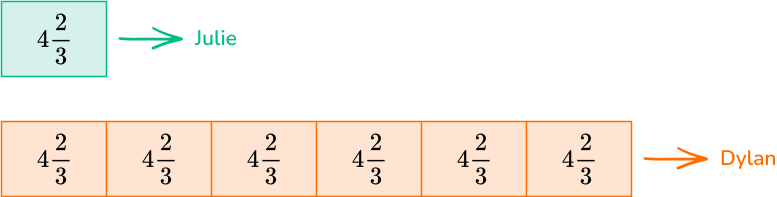
Dylan has 6 times the amount of yarn as Julie, which means 6 groups of 4 \, \cfrac{2}{3} \, .
\begin{aligned} & 6 \times 4 \, \cfrac{2}{3} \, = \\\\ & 6 \times \cfrac{14}{3} \, = \cfrac{84}{3}=28 \end{aligned}
Dylan has 28 feet of yarn.
6. Rory planted a vegetable garden. He planted 51 tomato plants and a third the amount of zucchini plants. How many zucchini plants did he plant?
16 zucchini plants

17 zucchini plants

18 zucchini plants

19 zucchini plants


Rory planted a third of the number of tomato plants which means 51 is divided into 3 equal groups.
51 \div 3=17
OR
\cfrac{1}{3} \, \times 51=17
Multiplicative comparison FAQs
No, you do not always have to write an equation. However, writing equations is a skill necessary for secondary mathematics.
The next lessons are
Still stuck?
At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.
Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.

Find out how we can help your students achieve success with our math tutoring programs.
[FREE] Common Core Practice Tests (3rd to 8th Grade)
Prepare for math tests in your state with these 3rd Grade to 8th Grade practice assessments for Common Core and state equivalents.
Get your 6 multiple choice practice tests with detailed answers to support test prep, created by US math teachers for US math teachers!