[FREE] Fun Math Games & Activities Packs
Always on the lookout for fun math games and activities in the classroom? Try our ready-to-go printable packs for students to complete independently or with a partner!
In order to access this I need to be confident with:
Addition and subtraction
Multiplying and dividing
FractionsMath formulas
Here you will learn about math formulas, including what math formulas are and how to use them.
Students will first learn about math formulas as part of measurement and data in 4th grade and 5th grade, and expand on that knowledge in geometry in 6th, 7th, and 8th grade.
What are math formulas?
Math formulas are rules that connect two or more variables. They are used to work out the values of unknown variables by substituting in other known values.
For example, here is a rectangle with base b and height h.

The formula for the perimeter P of a rectangle is:
P=2 \, (b+h)
We can use this formula to find the value of the perimeter by substituting in the values for the length and width of the rectangle.
List of math formulas
These are some of the measurement and geometry formulas you are most likely to encounter in grades 4-8.
Area \hspace{1.9cm}
Area of a rectangle | A=b \times h |  Where A is area, b is the base and h is the height. |
Area of a square | A=s \times s |  Where A is area and s is side. |
Area of a triangle | A=\cfrac{1}{2} \, b h | 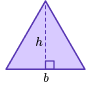 Where A is area, b is base and h is height. |
Area of a parallelogram | A=b \times h | 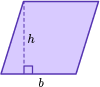 Where A is area, b is base and h is height. |
Area of a circle | A=\pi \times r^2 | 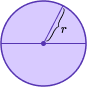 Where A is area and r is radius. |
Area of a trapezoid | A=\cfrac{1}{2} \, \left(b_1+b_2\right) h | 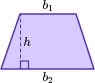 Where A is area, b_1 is base 1, b_2 is base 2 and h is height. |
Circumference \hspace{1.9cm}
Circumference of a circle | C=\pi d \;\;
C=2 \pi r |  Where C is circumference, d is diameter, r is radius. |
Perimeter \hspace{1.9cm}
Perimeter of a rectangle | P=2(b+h) |  Where P is perimeter, b is the base and h is the height. |
Perimeter of a square | P=4 s \hspace{1.35cm}
P=s+s+s+s |  Where P is perimeter and s is a side. |
Pythagorean Theorem \hspace{1.8cm}
Pythagorean Theorem | c^2=a^2+b^2 | 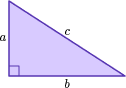 Where a is a side, b is a side and c is the hypotenuse. |
Surface Area \hspace{1.9cm}
Surface area of a cube | A=6 s^2 |  Where A is area, the variable s is the side and the 6 represents the number of faces of the cube. |
Volume \hspace{1.9cm}
Volume of a
| V=b \times h \times d |  Where V is the volume, b is the base, h is the height and d is the depth. |
Volume of a cube | v=s \times s \times s |  Where V is volume and s is side. |
Volume of a cylinder | V=\pi r^2 h | 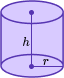 Where V is volume, r is radius of the circle and h is the height. |
Volume of a cone | V=\cfrac{1}{3} \, \pi r^2 h | 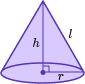 Where V is volume, r is radius of the circle and h is the height. |
Volume of a sphere | V=\cfrac{4}{3} \, \pi r^3 | 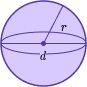 Where V is volume, and r is radius. |
What are math formulas?

![[FREE] Math Worksheets](https://thirdspacelearning.com/wp-content/uploads/2023/07/Algebra-check-for-understanding-quiz-listing-image-.png)
[FREE] Math Worksheets
![[FREE] Math Worksheets](https://thirdspacelearning.com/wp-content/uploads/2023/07/Algebra-check-for-understanding-quiz-listing-image-.png)
Use these quizzes to check your students’ understanding of math. Contains series of worksheets designed by math experts to identify areas of strength and support!
DOWNLOAD FREE![[FREE] Math Worksheets](https://thirdspacelearning.com/wp-content/uploads/2023/07/Algebra-check-for-understanding-quiz-listing-image-.png)
[FREE] Math Worksheets
![[FREE] Math Worksheets](https://thirdspacelearning.com/wp-content/uploads/2023/07/Algebra-check-for-understanding-quiz-listing-image-.png)
Use these quizzes to check your students’ understanding of math. Contains series of worksheets designed by math experts to identify areas of strength and support!
DOWNLOAD FREECommon Core State Standards
How does this relate to 4th grade math, 5th grade math, 6th grade math, 7th grade math, and 8th grade math?
- Grade 4: Measurement and Data (4.MD.A.3)
Apply the area and perimeter formulas for rectangles in real world and mathematical problems.
- Grade 5: Measurement and Data (5.MD.C.5b)
Apply the formulas V = l \times w \times h and V = b \times h for rectangular prisms to find volumes of right rectangular prisms with whole number edge lengths in the context of solving real world and mathematical problems.
- Grade 6: Geometry (6.G.A.2)
Find the volume of a right rectangular prism with fractional edge lengths by packing it with unit cubes of the appropriate unit fraction edge lengths, and show that the volume is the same as would be found by multiplying the edge lengths of the prism.
Apply the formulas V = l \times w \times h and V = b \times h to find volumes of right rectangular prisms with fractional edge lengths in the context of solving real-world and mathematical problems.
- Grade 7: Geometry (7.G.B.4)
Know the formulas for the area and circumference of a circle and use them to solve problems; give an informal derivation of the relationship between the circumference and area of a circle.
- Grade 8: Geometry (8.G.B.7)
Apply the Pythagorean Theorem to determine unknown side lengths in right triangles in real-world and mathematical problems in two and three dimensions.
- Grade 8: Geometry (8.G.C.9)
Know the formulas for the volumes of cones, cylinders, and spheres and use them to solve real-world and mathematical problems.
How to use math formulas
In order to solve with math formulas:
- Use the formula given in the question.
- Work carefully to answer the question, one step at a time.
- Write the final answer clearly.
Math formulas examples
Example 1: perimeter of a rectangle
Find the perimeter of the given rectangle using the formula, P=2 \, (b+h).

- Use the formula given in the question.
You will use the formula P=2 \, (b+h) to find the perimeter of the rectangle.
The length of the rectangle is 13 \, cm and the width is 5 \, cm, so substitute the measurements into the formula.
P=2 \, (13+5)
2Work carefully to answer the question, one step at a time.
P=2 \, (13+5)
Solve the operation within the parenthesis first. Adding 13 and 5 gives you 18.
P=2 \times 18
You will then multiply 2 \times 18.
This can also be solved as 18 + 18 to give the answer of 36.
P=36
3Write the final answer clearly.
The final answer is P = 36 \, cm.
The perimeter of the rectangle is 36 centimeters.
Example 2: area of a rectangle
Find the area of the rectangle given, using the formula A = b \times h.

Use the formula given in the question.
You will use the formula A = b \times h to find the area of the rectangle.
The length of the rectangle is 32 feet and the height is 17 feet.
Substitute the measurements into the formula.
A=32 \times 17
Work carefully to answer the question, one step at a time.
A=32 \times 17
You will multiply 32 by 17.
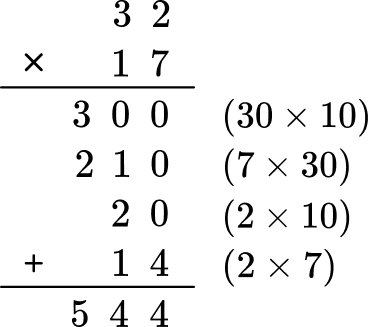
A = 544
Write the final answer clearly.
The final answer is A = 544 \, ft^2 .
The area of the rectangle is 544 square feet.
Example 3: area of a square
Find the area of the square given, using the formula A=s \times s.

Use the formula given in the question.
You will use the formula A=s \times s to find the area of the square.
The side of the square is 17 centimeters. Substitute the measurement into the formula.
A=17 \times 17
Work carefully to answer the question, one step at a time.
A=17 \times 17
You will multiply 17 by 17.
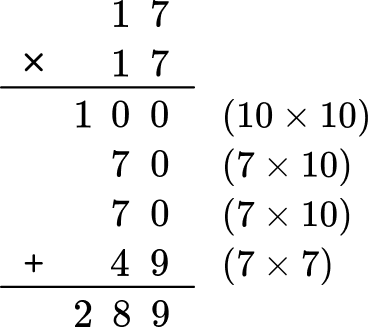
A = 289
Write the final answer clearly.
The final answer is A=289 \mathrm{~cm}^2 .
The area of the square is 289 square centimeters.
Example 4: volume of a rectangular prism
Find the volume of the rectangular prism using the formula, V = b \times h \times d.
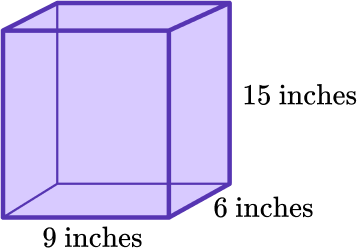
Use the formula given in the question.
You will use the formula V = b \times h \times d to find the volume of the rectangular prism.
The length of the prism is 9 inches, the width is 6 inches and the height is 15 inches. Substitute the measurements into the given formula.
V = 9 \times 6 \times 15
Work carefully to answer the question, one step at a time.
V=9 \times 6 \times 15
First, multiply the first two numbers using the knowledge of your multiplication facts, 9 \times 6 = 54.
Multiply 54 by 15 to calculate the volume of the rectangular prism.
V=54 \times 15
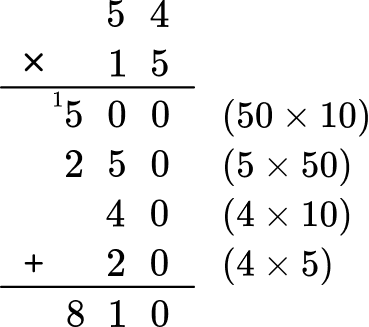
V=810 \text { inches }
Write the final answer clearly.
The final answer is V = 810 \text{ inches}^3.
The volume of the rectangular prism is 810 cubic inches.
Example 5: area of a triangle
Find the area of the triangle given, using the formula A=\cfrac{1}{2} \, b h.
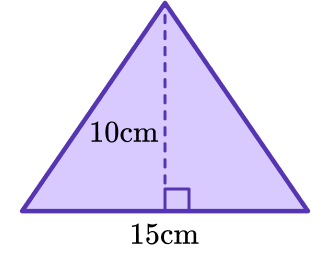
Use the formula given in the question.
You will use the formula A=\cfrac{1}{2} \, b h to find the area of the triangle.
The base of the triangle is 15 \, cm and the height of the triangle is 10 \, cm.
Substitute the measurement into the formula.
A=\cfrac{1}{2}\,(10 \times 15)
Work carefully to answer the question, one step at a time.
A=\cfrac{1}{2} \, (10 \times 15)
Following the order of operations, you will multiply 10 by 15 first.
10 \times 15=150
A=\cfrac{1}{2} \, (150)
Finally you will multiply 150 by \, \cfrac{1}{2} \, , or divide 150 by 2.
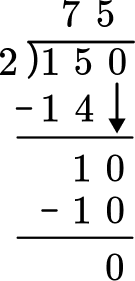
A = 75
Write the final answer clearly.
The final answer is A=75 \mathrm{~cm}.^2
The area of the triangle is 75 square centimeters.
Example 6: area of a parallelogram
Find the area of the parallelogram given, using the formula A = b \times h.
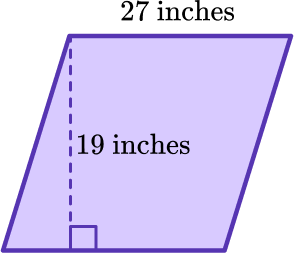
Use the formula given in the question.
You will use the formula A =b \times h to find the area of the parallelogram.
The base of the parallelogram is 27 inches and the height is 19 inches. Substitute the measurement into the formula.
A=27 \times 19
Work carefully to answer the question, one step at a time.
A=27 \times 19
To find the area, you will multiply 27 by 19.
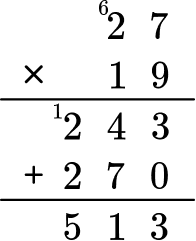
A = 513
Write the final answer clearly.
The final answer is A=513 \mathrm{~in}^2 .
The area of the parallelogram is 513 square inches.
Teaching tips for math formulas
- Formulas can be difficult for students to memorize. Always have a way for students to refer back to the formula, such as an anchor chart or a reference sheet, until they get familiar and comfortable with each formula.
- These basic math formulas will prepare students for work in high school with more complex numbers and formulas, including linear equations, the quadratic formula, and other algebra formulas, such as the slope-intercept formula.
- While using quizzes to assess a student’s knowledge of the different equations is important, consider making the assessments real-life, and have students measure items within the classroom or school, and use the formulas to calculate the area of the classroom or playground.
Easy mistakes to make
- Substituting in the wrong number in the equation
Learning the equation is important, but learning what each variable in an equation is equally important. In some basic math formulas, flipping the base and the height would still give students the same answer. However, as students move to more complex formulas, flipping of variables could result in incorrect answers.
For example, when finding the area of a trapezoid, flipping of a side versus the height would result in the wrong answer because the sides are added together and divided by 2, and the height is not.
- Take care with writing variables clearly
Neat writing is important. For example, the variables v and u can easily be muddled as they look similar and they both represent velocity in kinematic formulas.
Related math equations lessons
- Math equations
- One step equations
- One step equations with variables
- Solve equations with fractions
- Substitution
- Square root
Practice math formulas questions
1. Find the perimeter of the rectangle using the appropriate formula.

83 feet

166 feet

163 feet

85 feet

You will use the formula P=2 \, (b+h) to find the perimeter.
Substitute the values within the formula.
P=2 \, (32+51)
Add the values within the parenthesis first.
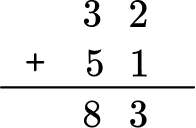
P=2 \, (83)
Then multiply 83 by 2.
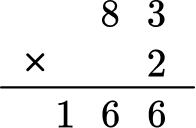
The final answer is P = 166 \, ft.
The perimeter of the rectangle is 166 feet.
2. Find the area of the rectangle using the appropriate formula.

2,747 feet^2

216 feet^2

2,647 feet^2

225 feet^2

You will use the formula A = b \times h to find the area of the rectangle.
Substitute in the values within the formula.
A=41 \times 67
Multiply 41 by 67.
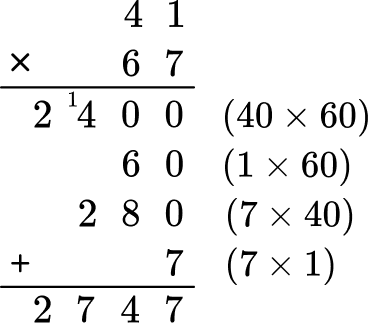
The final answer is A = 2,747 \, ft^2 .
The area of the rectangle is 2,747 feet^2.
3. Find the area of the square given, using the appropriate formula.

180 inches^2

1,825 inches^2

2,025 inches^2

225 inches^2

You will use the formula for finding the area of a square A=s \times s.
Substitute the value into the formula.
A=45 \times 45
You will multiply 45 by 45.
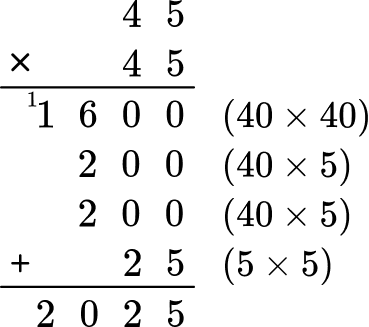
The final answer is A = 2,025 \, in^2 .
The area of the square is 2,025 inches^2.
4. Find the volume of the rectangular prism using the appropriate formula.
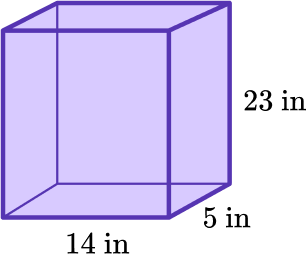
322 inches^3

1,510 inches^3

525 inches^3

1,610 inches^3

You will use the formula to find volume of the rectangular prism V=l \times w \times h.
Substitute the measurements into the given formula.
V=14 \times 5 \times 23
Multiply 14 \times 5, first.
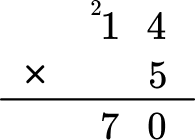
Then multiply the product of 14 and 5 by 23.
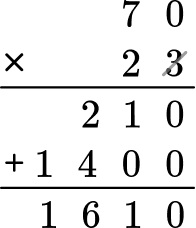
The final answer is V= 1,610 \, in^3 .
The volume of the rectangular prism is 1,610 inches^3.
5. Find the area of the triangle using the appropriate formula.
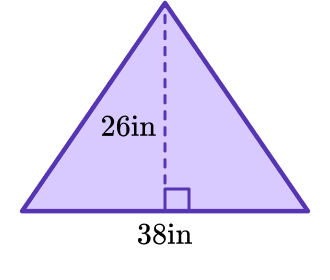
988 inches^2

114 inches^2

494 inches^2

524 inches^2

You will use the formula A=\cfrac{1}{2} \, b h to find the area of the triangle.
Substitute the measurements into the formula.
A=\cfrac{1}{2} \, (38 \times 26)
Following the order of operations, multiply 38 by 26 first.
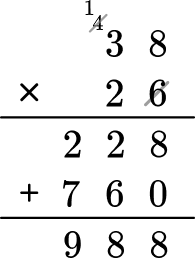
A=\cfrac{1}{2} \, (988)
Then multiply 988 by \,\cfrac{1}{2} \, , or divide 988 by 2.
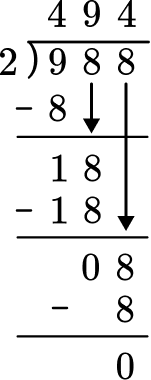
The final answer is A= 494 \, in^2 .
The area of the triangle is 494 inches^2.
6. Find the area of the parallelogram using the appropriate formula.
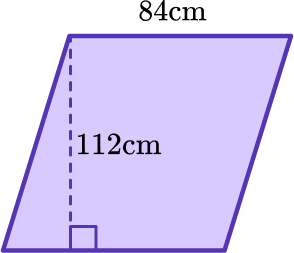




You will use the formula A=b \times h to find the area of the triangle.
Substitute the measurements into the formula.
A=84 \times 112
You will multiply 112 and 84 together to find the area of the quadrilateral.
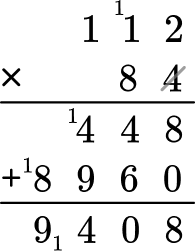
The final answer is A= 9,408 \, cm^2 .
The area of the parallelogram is 9,408 centimeters ^2.
Math formulas FAQs
The Pythagorean Theorem states that in any right triangle, the sum of the squares of the legs equals the square of the hypotenuse. If you know the lengths of any two sides of a right triangle, you can use the Pythagorean Theorem to find the third length.
The six functions of an angle, used in trigonometry, are sine, cosine, tangent, cotangent, secant, and cosecant.
The distance formula is a formula used to measure how far apart two objects or points are.
The next lessons are
Beyond elementary
You can use formulas in lots of different areas of math. One of the most famous formulas is the quadratic formula which we can use to solve quadratic equations.
x=\cfrac{-b \pm \sqrt{b^2-4 a c}}{2 a}
Quadratics are a type of polynomial and using coordinate geometry you can use them to produce a parabola shaped quadratic graph. We can use the graph to work out the solutions to the equation and the y-intercept of the graph.
Still stuck?
At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.
Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.

Find out how we can help your students achieve success with our math tutoring programs.
[FREE] Common Core Practice Tests (Grades 3 to 6)
Prepare for math tests in your state with these Grade 3 to Grade 6 practice assessments for Common Core and state equivalents.
40 multiple choice questions and detailed answers to support test prep, created by US math experts covering a range of topics!