Exponential Notation- Math Steps, Examples & Questions

[FREE] Fun Math Games & Activities Packs

Always on the lookout for fun math games and activities in the classroom? Try our ready-to-go printable packs for students to complete independently or with a partner!

DOWNLOAD FREE

In order to access this I need to be confident with:

Exponents Simplifying expressions Order of operations

Math resources Algebra Laws of exponents

Exponential notation

Here you will learn about exponential notation, including how to write an expression using exponential notation, simplify an expression written in exponent form, simplify expressions involving variables and exponential notations, and calculate the value of a term to the power of zero.

Students will first learn about exponential notation as a part of expressions and equations in $8$ th grade math, and will continue to expand on the knowledge throughout high school.

What is exponential notation?

Exponential notation, also known as scientific notation or exponential form, is a way of representing numbers (constants) and variables $(x$ and $y)$ that have been multiplied by themselves a number of times.

Examples of expressions involving exponential notation:

3^{4} \hspace{1cm} a^{5} \hspace{1cm} 2 x^{7} \hspace{1cm} \cfrac{1}{2}^{2 x} \hspace{1cm} \left(4 y^{2} x^{4}\right)^{7} \hspace{1cm} z^{-\frac{5}{2}}

Exponential notation is a simple way to express very large numbers or very small numbers. We use exponential notation, or exponents, to simplify expressions or solve equations involving powers, and is a simplified way to represent repeated multiplication and division.

For example,

Simplify $\bf{6 \times 6 \times 6 \times 6}$ .

$6$ is being multiplied by itself $4$ times (repeated multiplication).

Therefore write this as,

6^4

You would say this as $“6$ to the power of $4”$ .

For example,

Simplify $\bf{\textbf{x} \times \textbf{x} \times \textbf{x} \times \textbf{x} \times \textbf{x}}$ .

$x$ is being multiplied by itself $5$ times (repeated multiplication).

Therefore write this as,

x^5

You would say this as $“x$ to the power of $5”$ .

For example,

Simplify $\bf{2 \textbf{y} \times 2 \textbf{y} \times 2 \textbf{y} \times 2 \textbf{y}}$ .

In this question the term $2y$ is being multiplied by itself $4$ times (repeated multiplication).

Therefore write this as,

(2 y)^4

Decimal numbers can also be expressed using exponential notation. The standard form for a decimal number is $\text { a. } b \times 10^n.$

For example,

The number $0.0032$ can be written in exponential notation as $3.2 \times 10^{-3}.$

What are significant figures?

Significant figures are each of the digits of a number that are used to express it to the required degree of accuracy, starting from the first nonzero digit.

Mathematicians use significant figures to ensure that measurements and calculations are presented with precision and accuracy.

Some of the key rules for determining significant figures include:

All non-zero numbers are considered significant. For example, in the number $123,$ all three digits are significant $(1, 2, 3).$
Leading zeros are not considered significant. For example, in the number $0.0091,$ only the digits $9$ and $1$ are considered significant.
Trailing zeros in a whole number without a decimal point.

What is exponential notation?

Common Core State Standards

How does this relate to $8$ th grade math?

Grade 8: Expressions and Equations (8.EE.A.1)
Know and apply the properties of integer exponents to generate equivalent numerical expressions. For example, $32 \times 3–5 = 3–3 = \cfrac{1}{33} = \cfrac{1}{27}.$

[FREE] Exponential Notation Worksheet (Grade 6 to 8)

Use this worksheet to check your grade 6 to 8 students’ understanding of exponential notation. 15 questions with answers to identify areas of strength and support!

DOWNLOAD FREE

[FREE] Exponential Notation Worksheet (Grade 6 to 8)

Use this worksheet to check your grade 6 to 8 students’ understanding of exponential notation. 15 questions with answers to identify areas of strength and support!

DOWNLOAD FREE

How to simplify exponential notation

In order to simplify expressions involving exponential notation, you will:

Identify whether the base numbers for each term are the same.
Identify the operation(s) being used.
Simplify the expression, using the rules of exponential notation.

Simplifying exponential notations examples

Example 1: finding the value of an expression involving exponential notation and multiplication

Simplify $3^2 \times 3^3$ .

Identify whether the base numbers for each term are the same.

The base number is $3$ and is the same in each term.

2Identify the operation(s) being used.

The terms are being multiplied.

3Simplify the expression, using the rules of exponential notation.

$3^2$ is equivalent to $3 \times 3.$

$3^3$ is equivalent to $3 \times 3 \times 3.$

Therefore:

\begin{aligned}3^{2} \times 3^{3} &=3 \times 3 \times 3 \times 3 \times 3 \\\\ &=3^{5} \end{aligned}

Example 2: simplifying an expression involving unknowns and multiplication

Simplify $3 x^{2} \times 4 x^{3}$ .

Identify whether the base numbers for each term are the same.

The base number is $x$ and is the same in each term.

$3$ and $4$ are the coefficients of the $x$ terms.

Identify the operation(s) being used.

The terms are being multiplied.

Simplify the expression, using the rules of exponential notation.

$3 x^2$ is equivalent to $3 \times x \times x$ .

$4 x^3$ is equivalent to $4 \times x \times x \times x$ .

Therefore:

$\begin{aligned}3x^{2} \times 4x^{3} &= 3 \times x \times x \times 4 \times x \times x \times x \\\\ &= 3 \times 4 \times x \times x \times x \times x \times x \\\\ &= 12 \times x^{5} \\\\ &= 12x^{5}\end{aligned}$

Example 3: finding the value of an expression involving exponential notation and division

Simplify $6^5 \div 6^2$ .

Identify whether the base numbers for each term are the same.

The base number is $6$ and is the same in each term.

Identify the operation(s) being used.

The terms are being divided.

Simplify the expression, using the rules of exponential notation.

$6{ }^5$ is equivalent to $6 \times 6 \times 6 \times 6 \times 6$ .

$6{ }^2$ is equivalent $6 \times 6$ .

You can write $6{ }^5 \div 6{ }^2$ in the form,

$\cfrac{6^{5}}{6^{2}}$

Therefore:

$\begin{aligned}6^{5} \div 6^{2} &= \cfrac{6^{5}}{6^{2}} \\\\ &=\cfrac{6 \times 6 \times 6 \times 6 \times 6}{6 \times 6}\end{aligned}$

$6 \div 6=1,$ so keep canceling a $6$ on the top with a $6$ on the bottom until you are left with,

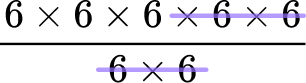
which is just $6 \times 6 \times 6=6^3.$

Example 4: simplifying an expression involving unknowns and division

Simplify $10 y^6 \div 5 y^4$ .

Identify whether the base numbers for each term are the same.

The base number is $y$ and is the same in each term.

Identify the operation(s) being used.

The terms are being divided.

Simplify the expression, using the rules of exponential notation.

$10 y^6$ is equivalent to $10 \times y \times y \times y \times y \times y \times y$ .

$5 y^4$ is equivalent to $5 \times y \times y \times y \times y$ .

Therefore:

$10y^{6} \div 5y^{4} = \cfrac{10 \times y \times y \times y \times y \times y \times y}{5 \times y \times y \times y \times y}$

Since $10 \div 5=2,$ and canceling the $y$ terms, we are left with

$\begin{aligned}\frac{10 \times y \times y \times y \times y \times y \times y}{5 \times y \times y\times y \times y} &= 2 \times y \times y \\\\\ &=2y^{2}\end{aligned}$

Example 5: simplifying an expression involving index notation and brackets

Simplify $\left(3^2\right)^3$ .

Identify whether the base numbers for each term are the same.

The base number is $3$ for the term inside the bracket.

Identify the operation(s) being used.

The term $3^2$ is “to the power of $3$ ”. $\left(3^2\right)^3$ is equivalent to $3^2 \times 3^2 \times 3^2.$

Simplify the expression, using the rules of exponential notation.

\begin{aligned}(3^{2})^{3} &= 3^{2} \times 3^{2} \times3^{2} \\\\ &= 3 \times 3 \times 3 \times 3 \times 3 \times 3 \\\\ &=3^{6}\end{aligned}

Example 6: simplifying an expression involving unknowns and brackets

Simplify $\left(2 z^3\right)^5$ .

Identify whether the base numbers for each term are the same.

The base number inside the brackets is $z.$

Identify the operation(s) being used.

The term $2 z^3$ is all “to the power of $5$ ”.

$\left(2 z^3\right)^5$ is equivalent to $2 z^3 \times 2 z^3 \times 2 z^3 \times 2 z^3 \times 2 z^3.$

Simplify the expression, using the rules of exponential notation.

\begin{aligned}(2z^{3})^{5} &= 2z^{3} \times 2z^{3} \times 2z^{3} \times 2z^{3} \times 2z^{3} \\\\ &= 2 \times z \times z \times z \times 2 \times z \times z \times z \times 2 \times z \times z \times z \times 2 \times z \times z \times z \times 2 \times z \times z \times z \\\\ &=32z^{15}\end{aligned}

Teaching tips for exponential notation

Use language that students can comprehend easily when discussing exponential notation. For example, emphasize that it’s a way to write very large or very small numbers easily, relate it to money or population growth so students can connect easily.

Compare exponential notation with standard notation with students and allow them to discuss the advantages and disadvantages of both.

Allow students to use technology, such as calculators and online resources, that allow them to practice and engage with exponential notation.

Easy mistakes to make

Shifting a decimal place in the wrong direction
The exponent indicates which way the number of places a decimal point should be shifted in the original number. Positive exponents shift the decimal place to the left, and negative exponents shift the decimal place to the right.
For example,
- $6 \times 10^4$ is equivalent to $6,000$ because you will shift the decimal place $4$ places to the left of the decimal.
- $1.4 \times 10^{-4}$ is equivalent to $0.00014$ because the decimal point will shift $4$ places.

Identifying the incorrect exponent power
If no exponent power is shown, remember it is being multiplied by itself ‘one time.
For example,
$2=2^{1}$

Not including coefficients and brackets when expanding brackets
For example,
$(2 x)^{3}$ ≠ $2 x^{3}$
This should be $(2x)^{3}=2x\times 2x\times 2x=8x^{3}$

Only using exponential notation with whole numbers
You can write fractions and decimals using exponential notation.
For example,
$\begin{array}{l}0.5^{3}=0.5 \times 0.5 \times 0.5=0.125=\cfrac{1}{8} \\\\ \left(\cfrac {1}{2}\right)^3=\cfrac{1}{2} \times \cfrac{1}{2} \times \cfrac{1}{2}=\cfrac{1}{8}\end{array}$

Exponential notation practice questions

8^{4}

32

32^{4}

4096^{4}

We are multiplying $8$ by itself $4$ times which can be written as $8^{4}.$

3a^{4}

(3a)^{4}

12a

12a^{4}

We are multiplying $3a$ by itself $4$ times which can be written as $(3a)^{4}.$

8x^{11}

15x^{30}

8x^{11}

15x^{11}

$3$ and $5$ are the coefficients being multiplied in this expression.

\begin{aligned} 5 x^5&=5 \times x \times x \times x \times x \times x \\\\ 3 x^6&=3 \times x \times x \times x \times x \times x \times x  \\\\ 5 x^5 \times 3 x^6&=5 \times x \times x \times x \times x \times x \times 3 \times x \times x \times x \times x \times x \times x \\\\ \quad&=15 x^{11} \end{aligned}

z^{\frac{5}{3}}

z^{2}

z^{-2}

2

The base $z$ is being divided in this expression.

$z^5$ is equivalent to $z \times z \times z \times z \times z.$

$z^3$ is equivalent to $z \times z \times z.$

Therefore,

\begin{aligned}z^{5} \div z^{3} &= \cfrac{z \times z \times z \times z \times z}{z \times z \times z} \\\\ &=z^{2}\end{aligned}

3c^{8}

6c^{8}

9c^{8}

6c^{6}

The term $3c^{4}$ is “to the power of $2$ ”.

$(3c^{4})^{2}$ is equivalent to $(3c^{4})^{2} = 3c^{4} \times 3c^{4}.$

\begin{aligned}(3c^{4})^{2} &= 3c^{4} \times 3c^{4} \\\\ &=3 \times c \times c \times c \times c \times 3 \times c \times c \times c \times c \\\\ &=9c^{8}\end{aligned}

6 a^3

9 a^6

9 a^3

6 a^6

The term $3 a^3$ is all “to the power of $2$ ”.

$\left(3 a^3\right)^2$ is equivalent to $\left(3 a^3\right)^2=3 a^3 \times 3 a^3.$

\begin{aligned} 3 a^3 \times 3 a^3&=3 \times a \times a \times a \times 3 \times a \times a \times a \\\\ & =9 a^6\end{aligned}

Exponential notation FAQS

What are significant figures?

Significant figures are each of the digits of a number that are used to express it to the required degree of accuracy, starting from the first nonzero digit.

What is the difference between exponential notation and engineering notation?

Exponential notation is a general concept that is used across various fields, while engineering notation is a more specific form of exponential notation that is commonly used within the engineering field.

The next lessons are

Radical functions
Math formulas
Quadratic graphs
Straight line graphs

Still stuck?

At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.

Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.