Laws of exponents

Here you will learn about the laws of exponents, including what the laws of exponents are and how you can use them. You’ll also learn how to write an expression using exponential notation and how to find the cube root of an integer.

Students will first learn about the laws of exponents in 8 th grade and will continue to expand on that knowledge throughout high school.

What are the laws of exponents?

Laws of exponents provide us with rules for simplifying calculations or expressions involving powers of the same base. This means that the larger number or letter must be the same.

For example,

This is because 2^{5} \times 2^{3} means (2 \times 2 \times 2 \times 2 \times 2) \times (2 \times 2 \times 2). If you count up all the 2 ’s, you can see that there are eight of them or 2^{8}.

This is because x^{10} \div x^{4} means \cfrac{x \times x \times x \times x \times x \times x \times x \times x \times x \times x} {x \times x \times x \times x} , the four x ’s on bottom cancel with four x ’s on the top, leaving you with six x ’s on top or x^{6}.

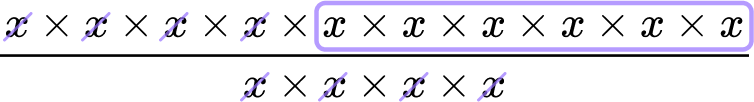
You cannot use laws of exponents to evaluate calculations when the bases are different.

For example,

There are several laws of exponents (sometimes called exponent laws or rules of exponents), but this page will cover product rule, quotient rule, and negative exponent rule.

1. Power of a product rule: multiplying exponents

When multiplying exponents with the same base, add the powers.

Step by step guide: Multiplying exponents

2Power of a quotient rule: dividing exponents.

When dividing exponents with the same base, use subtraction to subtract the powers.

Step by step guide: Dividing exponents

When the exponent is a negative number, put it over 1 and flip (write its reciprocal) to make it positive.

Step by step guide: Negative exponents

Exponential notation

Exponential notation is a way of representing numbers (constants) and variables (x and y) that have been multiplied by themselves a number of times.

Examples of expressions involving exponential notation:

Exponential notation is a simple way to express very large numbers or very small numbers.

For example,

Simplify \bf{6 \times 6 \times 6 \times 6}

6 is being multiplied by itself 4 times (repeated multiplication).

Therefore, write this as

You would say this as “6 to the power of 4”

Step by step guide: Exponential notation

Cube root

The cube root is the number that is multiplied to itself three times to get a number.

Similarly, square root is a number multiplied to itself two times to get a number.

The table shows some square roots and cube roots.

Roots can be expressed as exponents. For example, \sqrt{4} can be rewritten as (4)^{\frac{1}{2}}.

The same is true for cube root, the \sqrt[3]{8} can be rewritten as (8)^{\frac{1}{3}}. Notice, how the denominator of the exponent is the same as the index of the root.

The way you simplify cube roots is similar to the way you simplify square roots.

(9)^{\frac{1}{2}}=3 because 9 is a perfect square and 3 \times 3 = 9.

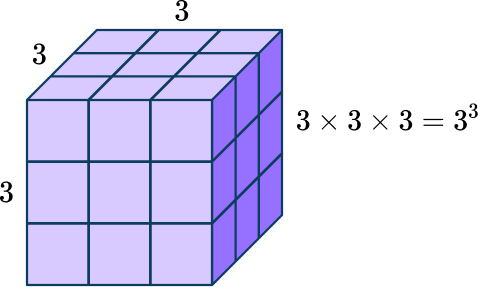
(27)^{\frac{1}{3}}=3 because 27 is a perfect cube and 3 \times 3 \times 3=27.

You can visualize a perfect cube as,

What if you have to evaluate a cube root of a number that is not a perfect cube?

For example, \sqrt[3]{16} which is the same as (16)^{\frac{1}{3}}. There is no integer multiplied to itself three times that is equal to 16. So, think about which perfect cube numbers are a factor of 16.

8 is a factor of 16 and a perfect cube, so you can break up 16 to be, \sqrt[3]{8 \times 2}=\sqrt[3]{8} \times \sqrt[3]{2}

\sqrt[3]{8}=2 so, the expression can be rewritten to be 2 \sqrt[3]{2} or 2(2)^{\frac{1}{3}}.

Let’s look at cube roots of algebraic expressions.

\sqrt[3]{x^3} can be rewritten as \left(x^3\right)^{\frac{1}{3}} .

Using laws of exponents, you can multiply the exponents together.

x^3 is a perfect cube because x \times x \times x is x^3.

Let’s look at another example.

If you notice, the expression is simplified by the exponent being divided by 3 or multiplied by \frac{1}{3}.

Let’s look at an example when the exponent is not divisible by 3.

You can rewrite the expression so that part of it has an exponent that is divisible by 3.

A number or variable that is ‘cubed’ is multiplied by itself three times.

Step by step guide: Square root

Step by step guide: Cube root

What are the laws of exponents?

Common Core State Standards

How does this relate to 8 th grade and high school math?

• Grade 8: Expressions and Equations (8.EE.A.1)
  Know and apply the properties of integer exponents to generate equivalent numerical expressions. For example, 32 \times 3-5 = 3-3 = \cfrac{1}{33} = \cfrac{1}{27} \, .

• High School – The Real Number System (HSN-RN.A.1)
  Explain how the definition of the meaning of rational exponents follows from extending the properties of integer exponents to those values, allowing for a notation for radicals in terms of rational exponents.
  
  For example, we define \cfrac{51}{3} to be the cube root of 5 because we want \left(\cfrac{51}{3}\right)3=5 \left(\cfrac{1}{3}\right)3 to hold, so \left(\cfrac{51}{3}\right)3 must equal 5.

How to use the laws of exponents

There are a lot of ways to use the laws of exponents to solve equations. For more specific step-by-step guides, check out the laws of exponents pages linked in the “What are the laws of exponents?” section above or read through the examples below.

Laws of exponents examples

Example 1: multiplying exponents

Simplify,

1. Add the exponents.

Add together the exponents 3 and 2.

2Multiply any coefficients.

Multiply 4 and 7 together.

So,

This can also be written as

Example 2: dividing exponents

Simplify

Example 3: negative exponents

Simplify and leave your answer in index form.

Example 4: negative exponents

Simplify

Notice how the index affects the entire bracket

Example 5: simplifying an expression involving unknowns and multiplication

Simplify

Example 6: cube root

Simplify the expression \sqrt[3]{24}.

Teaching tips for laws of exponents

• Start with reviewing what exponents are and make sure students are comfortable with working with exponents before introducing the different laws of exponents.

• While worksheets have their place in the classroom, consider using interactive activities that allow students to actively apply the different laws. This can include class discussions with an online platform to increase participation.

• The use of mnemonic devices can help students remember the laws. Allow students to be creative and come up with their own.

Easy mistakes to make

• Using the multiplication and division laws with terms with different bases
  The multiplication and division laws of exponents can only be used with terms with the same base. For example, you cannot simplify a^{4} \times b^{3} as the bases are different.

• Not raising all terms inside the parenthesis to the power that is outside the parentheses.
  When you simplify, remember to square both the 4 and the a. It is common to forget to square the 4.
  For example,
  (4a)^{2}
  (4 a)^{2}=4 a \times 4 a=4^{2} a^{2}=16 a^{2}
  The brackets mean the entire term is squared.

• Confusing laws of exponents with properties of exponents
  The two concepts are closely related, however, the properties of exponents refer to the specific behaviors and characteristics of expressions involving exponents. The laws of exponents are general rules that encompass several properties of exponents.

• Confusing positive and negative powers
  You can have decimal, fractional, negative or positive integers (exponents).

The next lessons are

• Math formulas
• Scientific notation
• Quadratic graphs
• Factoring
• Radicals
• Exponent rules
• Anything to the power of  0
• Distributing exponents

Still stuck?

At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.

Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.

Find out how we can help your students achieve success with our math tutoring programs.