Radicals

Here we will learn about radicals, including simplifying radicals, adding and subtracting radicals, multiplying radicals, dividing radicals and rationalizing radicals.

Students are first exposed to a radical, or square root in 8 th grade when taking the square root of numbers. However, they greatly expand that knowledge in algebra class.

What are radicals?

Radicals (or sometimes referred to as surds) are represented by \sqrt{\;\;} and are used to calculate the square root or the nth root of numbers and expressions. Expressions with \sqrt{\;\;} are called radical expressions.

For example, \sqrt{16}=4 because 16 is a perfect square number. Perfect square numbers have whole number roots.

However, \sqrt{5} \approx 2.23606 \ldots is an irrational number because it’s a non-terminating, non-repeating decimal that cannot be expressed as a fraction.

Simplifying radicals and exact calculations

You can simplify the number under the radical to an exact calculation. For example, let’s apply the Pythagorean Theorem to find the missing length of the triangle.

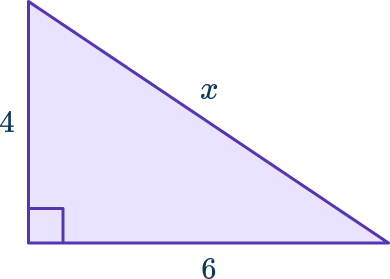
Notice how 52 is not a perfect square number. One way to find the answer is to type \sqrt{52} into a calculator.

Another strategy is to simplify the number under the radical. That means to find the largest square root factor of 52.

Here are some perfect square numbers: 4, 9, 16, 25, 36, 49, 64, 81, 100, 121, 144, 169, …

4 is the largest perfect square factor of 52.

\sqrt{52}=2 \sqrt{13} \rightarrow simplified radical expression or exact form

You can also simplify radical expressions that contain variables.

For example, let’s simplify the expression, \sqrt{4 x^3}

4 is a perfect square number so that is simple enough to do. However, how do you simplify x^3? Variables raised to even exponents are considered perfect square expressions.

If you notice, x^3 does not have an even exponent. However, you can break it apart so that it does.

\sqrt{4 x^3} simplified is 2 x \sqrt{x}

Step-by-step guide: How to simplify radicals

Adding and subtracting radical expressions

In order to add and subtract radical expressions, the number or expression under the radical symbol must be the same.

For example, 14 \sqrt{6}-6 \sqrt{6} can be subtracted because both radicals are identical.

So, 14 \sqrt{6}-6 \sqrt{6}=8 \sqrt{6}

Do not add or subtract the number under the radical. It remains the same.

If the number or expression under the radical is not the same, you must use strategies for simplifying the radical in order to add or subtract them.

For example, 5 \sqrt{12}+2 \sqrt{27} cannot be added the way it is written because the radicals do not match.

In this case, the radicals simplify to be the same. So, they can now be added.

Step-by-step guide: Adding radicals

Step-by-step guide: Subtracting radical

Multiplying and dividing radicals

Unlike addition and subtraction, the radicals do not have to match when multiplying or dividing. You can also multiply and divide the numbers under the radicals.

For example, 6 \sqrt{7} \cdot 9 \sqrt{2}=54 \sqrt{14} \rightarrow The numbers outside the radicals multiply together and the numbers under the radicals multiply together.

Always remember to look at the final product to see if it can be simplified. In this case, the product cannot be simplified any further because there is not a perfect square factor of 14.

Let’s look at another example. \cfrac{16 \sqrt{24}}{4 \sqrt{2}}=4 \sqrt{12}

When dividing, the numbers outside of the radicals can divide one another and the numbers inside the radicals can divide one another. In this case, notice how the quotient can be simplified.

Step-by-step guide: Multiplying radicals

Step-by-step guide: Dividing radicals

Rationalizing the denominator

Expressions that have radicals in the denominator must be rationalized. This means that an equivalent expression has to be created so that it does not have a radical in the denominator.

Let’s look at the expression \cfrac{\sqrt{15}}{\sqrt{6}}, notice how 6 does not divide evenly into 15.

So, division does not work in this case. The radical cannot remain in the denominator so there is another strategy you can use to rationalize the expression.

Multiply the numerator and denominator by the radical in the denominator, which is \sqrt{6}. The goal is to find an equivalent expression that does not have a radical in the denominator.

Multiplying the numerator and denominator by \sqrt{6} is like multiplying the expression by \cfrac{\sqrt{6}}{\sqrt{6}} which is 1.

\cfrac{\sqrt{15}}{\sqrt{6}}=\cfrac{3 \sqrt{10}}{6} \rightarrow the radical is no longer in the denominator

However, the expression \cfrac{3 \sqrt{10}}{6} can be simplified further. Notice how the 3 in the numerator and the 6 in the denominator can be simplified.

So, \cfrac{\sqrt{15}}{\sqrt{6}}=\cfrac{3 \sqrt{10}}{6}=\cfrac{\sqrt{10}}{2}

Step-by-step guide: Rationalize the denominator

What are radicals?

Common Core State Standards

How does this relate to high school math?

• Number and Quantity – High School: (HSN-RN.B.3)
  Explain why the sum or product of two rational numbers is rational; that the sum of a rational number and an irrational number is irrational; and that the product of a nonzero rational number and an irrational number is irrational.

How to use radicals

There are lots of different ways we can calculate with radicals. We can:

• Simplify radicals and use them in exact calculations
• Add and subtract radical expressions
• Multiply and divide radicals
• Rationalize the denominator of radicals

Let’s have a look at each one in more detail.

Simplifying radical examples

Example 1: simplifying square roots

Simplify the expression: \sqrt{60}

1. Find the largest square factor(s) of the term under the root.

Square numbers are 1, 4, 9, 16, 25, …

The largest square factor of 60 is 4 because 4 \times 15=60

2Rewrite the radical as a product of the square factor(s) and the other factors.

\begin{aligned}\sqrt{60} & =\sqrt{4 \times 15} \\\\ & =\sqrt{4} \times \sqrt{15}\end{aligned}

3Simplify the radical expression.

\sqrt{60} =\sqrt{4} \times \sqrt{15} \;\; (4 is a perfect square so take the square root of 4 to simplify )

\hspace{0.8cm} =2 \sqrt{15}

\sqrt{60} simplifies to be 2 \sqrt{15}

Example 2: simplifying algebraic expression

Simplify the expression: \sqrt{16 x^5}

Adding and subtracting radicals examples

Example 3: add with unlike radicals

Add the expressions: 2\sqrt{5}+\sqrt{45}

Example 4: subtract with unlike radicals

Subtract the expressions: \sqrt{18}-10 \sqrt{2}

Multiplying and dividing radicals examples

Example 5: dividing radicals

Divide the radical expression.

Example 6: multiplying radicals expanding brackets

Multiply the radical expression.

Rationalizing radical expressions examples

Example 7: rationalize the denominator

Simplify the radical expression.

Example 8: rationalize the denominator using the conjugate

Simplify the expression by rationalizing the denominator.

Teaching tips for radicals

• Reinforce perfect square numbers with students.
• Review with students how to break numbers down into their factors.
• Use digital platforms such as Desmos to help students develop conceptual understanding.
• Have students practice problems by using interactive digital platforms such as Khan Academy.

Easy mistakes to make

• Thinking that the square root is dividing a number by \bf{2}
  For example, \sqrt{16} ≠ 8
  \sqrt{16}=4 because 4 \times 4=16

• Rewriting the number under the square root sign (the radicand) as a product of any two factors
  In order to simplify a radical, it has to be a perfect square or has to have a perfect square factor. So, one of these factors must be a square number.
  
  To simplify \sqrt{40} , break 40 so that one of the factors is a perfect square. The largest square factor of 40 is 4.
  
  \begin{aligned}\sqrt{40} & =\sqrt{4} \times \sqrt{10} \\\\ & =2 \times \sqrt{10} \\\\ & =2 \sqrt{10}\end{aligned}

• Not simplifying fully
  Always check that there are no square factors of the number under the root.
  For example,
  
  \begin{aligned}\sqrt{32} & =\sqrt{4} \times \sqrt{8} \\\\ & =2 \times \sqrt{8} \\\\ & =2 \sqrt{8}\end{aligned}
  
  This expression is not fully simplified because the number under the radical, 8, can be simplified further. 4 is a perfect square factor of 8.
  
  So, 2 \sqrt{8}=2 \times \sqrt{4} \times \sqrt{2}=2 \times 2 \times \sqrt{2}=4 \sqrt{2}

• Remembering that a radical or root with no integer coefficient is ‘ \bf{1} lot’ of that surd
  As in algebra, we understand that a actually means 1a. So, \sqrt{2} means 1 \times \sqrt{2}

• Mixing up addition and multiplication laws
  With addition, the radicals have to match and only the numbers in front of the radicals can be added \rightarrow \sqrt{3}+\sqrt{3}=2 \sqrt{3}
  
  With multiplication, both the numbers inside and outside the radicals are multiplied together \rightarrow \sqrt{3} \times \sqrt{3}=\sqrt{9}=3
  
  Refer back to knowledge of algebra to help: a+a=2 a and a \times a=a^2 \text {.}

• Trying to combine unlike radicals
  For example, \sqrt{3}+\sqrt{5} ≠ \sqrt{8} , just leave the expression as \sqrt{3}+\sqrt{5}

The next lessons are

• Rational functions
• Vectors
• Quadratic equations
• Trigonometry

Still stuck?

At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.

Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.

Find out how we can help your students achieve success with our math tutoring programs.