High Impact Tutoring Built By Math Experts
Personalized standards-aligned one-on-one math tutoring for schools and districts
In order to access this I need to be confident with:
Exponents Negative exponents Multiplication and divisionExponent rules
Here you will learn about exponent rules, including what each exponent rule is and how to apply an exponent rule to an exponential expression.
Students will first learn about exponent rules as part of expressions and equations in grade 8.
What are exponent rules?
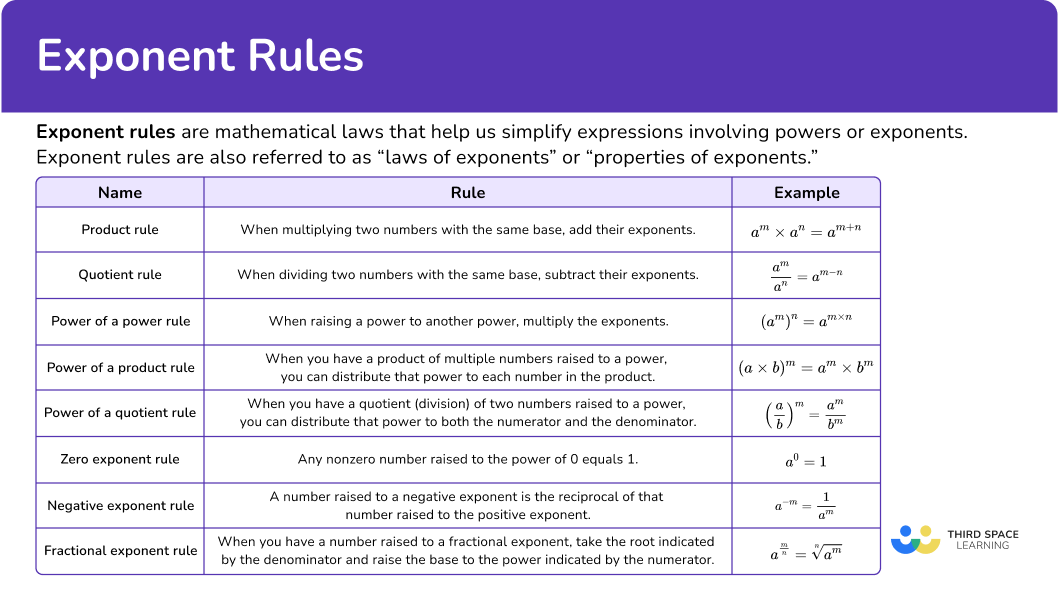
Exponent rules are mathematical laws that help us simplify expressions involving powers or exponents. Exponent rules are also referred to as “laws of exponents” or “properties of exponents.”
There are many different rules of exponents; these involve properties such as multiplication, division, raising to a power, and dealing with zero and negative exponents. These rules help us work with exponents in a more organized way, making math easier and letting us solve all sorts of problems efficiently.
What are exponent rules?
Common Core State Standards
How does this relate to 8 th grade math?
- Grade 8 – Expressions and Equations (8.EE.A.1)
Know and apply the properties of integer exponents to generate equivalent numerical expressions. For example, 32 \times 3-5=3-3= \cfrac{1}{33}=\cfrac{1}{27}.
![[FREE] Exponents Worksheet (Grade 4 to 6)](https://thirdspacelearning.com/wp-content/uploads/2023/07/Exponents-check-for-understanding-quiz-listing-image.png)
[FREE] Exponents Worksheet (Grade 4 to 6)
Use this quiz to check your grade 4 to 6 students’ understanding of exponents. 15+ questions with answers covering a range of 4th and 6th grade exponents topics to identify areas of strength and support!
DOWNLOAD FREE [FREE] Exponents Worksheet (Grade 4 to 6)
Use this quiz to check your grade 4 to 6 students’ understanding of exponents. 15+ questions with answers covering a range of 4th and 6th grade exponents topics to identify areas of strength and support!
DOWNLOAD FREEHow to use exponent rules
In order to simplify an expression using exponent rules:
- Identify the base and the exponent.
- Apply the appropriate exponent rule(s) according to the operation.
- Perform the arithmetic operations indicated by the exponent rules to simplify the expression.
Exponent rules examples
Example 1: product rule
Evaluate the expression.
3^3 \times 3^2- Identify the base and the exponent.
Base (first term): 3
Base (second term): 3
Exponent: (first term): 3
Exponent: (second term): 2
2Apply the appropriate exponent rule(s) according to the operation.
Since you are multiplying two terms with the same base, you can use the product rule which says to add the two exponents: a^m \times a^n=a^{m+n}
3Perform the arithmetic operations indicated by the exponent rules to simplify the expression.
\begin{aligned}&3^3 \times 3^2=3^{3+2}=3^5 \\\\ &3^5=3 \times 3 \times 3 \times 3 \times 3=243\end{aligned}Example 2: quotient rule
Evaluate the expression.
6^5 \div 6^3Identify the base and the exponent.
Base (first term): 6
Base (second term): 6
Exponent: (first term): 5
Exponent: (second term): 3
Apply the appropriate exponent rule(s) according to the operation.
Since you are dividing two numbers with the same base, you can use the quotient rule which says to subtract the exponents: a^m \div a^n=a^{m-n}
Perform the arithmetic operations indicated by the exponent rules to simplify the expression.
Example 3: power of a power rule
Evaluate the expression.
\left(10^2\right)^3Identify the base and the exponent.
Base: 10^2
Exponent: 3
Apply the appropriate exponent rule(s) according to the operation.
Since you are raising a power to another power, you can use the power of a power rule, which says to multiply the exponents: \left(a^m\right)^n=a^{m \times n}
Perform the arithmetic operations indicated by the exponent rules to simplify the expression.
Example 4: power of a product rule
Evaluate the expression.
(4 \times 3)^2Identify the base and the exponent.
Base: 4 \times 3
Exponent: 2
Apply the appropriate exponent rule(s) according to the operation.
Since there is a product of multiple numbers raised to a power, you can use the power of a product rule which says you can distribute that power to each number in the product: (a \times b)^m=a^m \times b^m
Perform the arithmetic operations indicated by the exponent rules to simplify the expression.
Example 5: power of a quotient rule
Evaluate the expression.
(12 \div 4)^6Identify the base and the exponent.
Base: 12 \div 4
Exponent: 6
Apply the appropriate exponent rule(s) according to the operation.
Since you have a quotient (division) of two numbers raised to a power, you can use the power of a quotient rule which says you can distribute that power to both the numerator and the denominator: \left(\cfrac{a}{b}\right)^m=\cfrac{a^m}{b^m}
Perform the arithmetic operations indicated by the exponent rules to simplify the expression.
Example 6: zero exponent rule
Evaluate the expression.
18^0Identify the base and the exponent.
Base: 18
Exponent: 0
Apply the appropriate exponent rule(s) according to the operation.
Since you have a number raised to the power of 0, you can use the zero exponent rule, which says it equals 1: a^0=1
Perform the arithmetic operations indicated by the exponent rules to simplify the expression.
Example 7: negative exponent rule
Evaluate the expression.
5^{-4}Identify the base and the exponent.
Base: 5
Exponent: –4
Apply the appropriate exponent rule(s) according to the operation.
Since you have a number raised to a negative exponent, you can use the negative exponent rule, which says the answer is the reciprocal of that number raised to the positive exponent: a^{-m}=\cfrac{1}{a^m}
Perform the arithmetic operations indicated by the exponent rules to simplify the expression.
Example 8: fractional exponent rule
Evaluate the expression.
9^{3 / 2}Identify the base and the exponent.
Base: 9
Exponent: \cfrac{3}{2}
Apply the appropriate exponent rule(s) according to the operation.
Since you have a number raised to a fractional exponent, you can use the fractional exponent rule, which says to take the root indicated by the denominator and raise the base to the power indicated by the numerator: a^{m / n}=\sqrt[n]{a^m}
Perform the arithmetic operations indicated by the exponent rules to simplify the expression.
Teaching tips for exponent rules
- Begin by ensuring students understand what exponents represent. Reinforce the idea that exponents indicate repeated multiplication.
- Start with small numbers (bases and exponents) and gradually progress to larger numbers and more complex expressions.
- Print out an anchor chart listing each exponent rule for students to refer to when completing worksheets.
Easy mistakes to make
- Ignoring the order of operations
When simplifying exponential expressions, it is important to keep note of the order of operations, especially keeping an eye out for parentheses in which anything inside should be performed first.
- Forgetting the zero exponent rule
Students commonly forget that a non-zero base raised to the zero power equals 1, which can lead to calculation errors.
- Confusing product and power rules.
Confusing the product rule (adding exponents when multiplying powers with the same base) with the power rule (multiplying exponents when raising a power to another power).
Related laws of exponents lessons
Practice exponent rules questions
1. Which expression is equivalent to (4 \times 8)^2 ?
The power of a product rule states that when you have a product of multiple numbers raised to a power, you can distribute that power to each number in the product.
Therefore, (4 \times 8)^2=4^2 \times 8^2
2. Solve the equation.
15+12^0= \; ?
The zero rule says that any number raised to the power of zero equals one. Therefore, 12^0=1
When you add 1 to 15, you get 16.
3. Which expression is equivalent to 5^2 \times 5^9?
The product rule says that when multiplying two numbers with the same base, add their exponents.
Therefore, 5^2 \times 5^9=5^{(2+9)}=5^{11}
4. Which expression is equivalent to (9 \div 3)^3?
The power of a quotient rule states that when you have a quotient (division) of two numbers raised to a power, you can distribute that power to both the numerator and the denominator (the dividend and the divisor).
That means that since the entire division expression of 9 \div 3 is being cubed, or raised to the third power, we can distribute the power to the 9 and the 3.
Then we can solve:
(9 \div 3)^3=9^3 \div 3^3=729 \div 27=27
5. Which exponent is equivalent to \left(6^3\right)^5?
The power of a power rule states that when raising a power to another power, you multiply the exponents.
Therefore, \left(6^3\right)^5=6^{3 \times 5}=6^{15}
6. How would you use the quotient rule to solve 8^9 \div 8^7?
Add the exponents to make it 8^{16}.
Subtract the exponents to make it 8^{2}.
Turn the exponents into a fraction to make it 8^{\frac{9}{7}}.
Turn the exponents into a negative exponent to make it 8^{-2}.
The quotient rule states that when dividing two numbers with the same base, subtract their exponents.
Therefore, 8^9 \div 8^7=8^{9-7}=8^2
7. Which is equivalent to 10^{-5}?
The negative exponent rule states that a number raised to a negative exponent is the reciprocal of that number raised to the positive exponent.
Therefore, 10^{-5}=\cfrac{1}{10^5}
8. Which is equivalent to 6^{\frac{4}{5}}?
The fractional exponent rule states that when you have a number raised to a fractional exponent, you take the root indicated by the denominator and raise the base to the power indicated by the numerator.
Therefore, 6^{\frac{4}{5}}=\sqrt[5]{6^4}
Exponent rules FAQs
Exponent rules are mathematical laws that help us simplify expressions involving powers or exponents. Exponent rules are also referred to as “laws of exponents” or “properties of exponents.”
The negative exponent rule states that any number raised to a negative power can be rewritten as the reciprocal of the same number raised to the corresponding positive power.
No, exponent rules apply to various types of numbers, including real numbers, complex numbers, rational numbers, and more.
Exponent rules and logarithms are closely related because they are inverse operations of each other. Logarithms allow us to solve for exponents, and exponent rules help simplify expressions involving logarithms.
The next lessons are
Still stuck?
At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.
Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.
Find out how we can help your students achieve success with our math tutoring programs.
[FREE] Common Core Practice Tests (3rd to 8th Grade)
Prepare for math tests in your state with these 3rd Grade to 8th Grade practice assessments for Common Core and state equivalents.
Get your 6 multiple choice practice tests with detailed answers to support test prep, created by US math teachers for US math teachers!