[FREE] Fun Math Games & Activities Packs
Always on the lookout for fun math games and activities in the classroom? Try our ready-to-go printable packs for students to complete independently or with a partner!
In order to access this I need to be confident with:
Right triangles Substitution ExponentsPowers and roots
Rounding decimalsPythagorean Theorem
Here you will learn about the Pythagorean Theorem, including how to find side measurements of a right triangle and using Pythagoras’ theorem to check and see if a triangle has a right angle or not.
Students will first learn about Pythagorean Theorem as part of geometry in 8 th grade and continue to use it in high school.
What is the Pythagorean Theorem?
The Pythagorean Theorem states that the square of the longest side of a right triangle (called the hypotenuse) is equal to the sum of the squares of the other two sides.
Pythagorean Theorem formula shown with triangle ABC is:
a^2+b^2=c^2

Side c is known as the hypotenuse. The hypotenuse is the longest side of a right triangle. Side a and side b are known as the adjacent sides. They are adjacent, or next to, the right angle.
You can only use the Pythagorean Theorem with right triangles.
For example,
Let’s look at this right triangle:
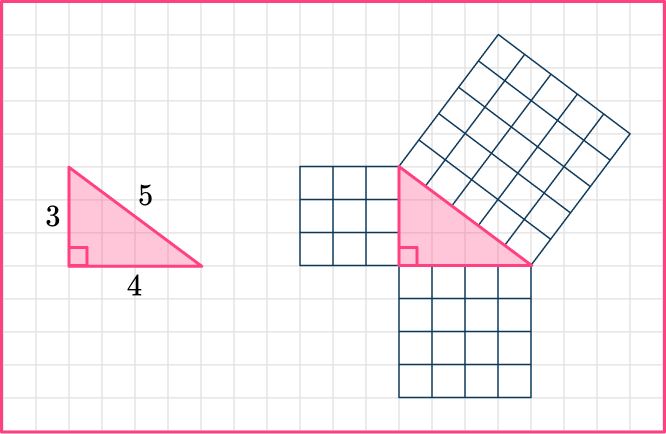
Above, three square grids have been drawn next to each of the sides of the triangle.
The area of the side of length 3=3 \times 3=3^2=9
The area of the side of length 4=4 \times 4=4^2=16
The area of the side of length 5=5 \times 5=5^2=25
The sum of the areas of the squares on the two shorter sides is equal to the area of the square on the longest side.
9+16=25
When you square the sides of the two shorter sides of a right triangle and add them together, you get the square of the longest side.
3^2+4^2=5^2
3, 4, 5 is known as a Pythagorean triple.
There are other Pythagorean triples such as 5, 12, 13 and 8, 15, 17.
If you know two lengths of a right triangle, you can use Pythagorean Theorem to work out the length of the third side.
Pythagorean Theorem Proof
Use the drawing of a square with a smaller square shown inside with the proof below.

The area of each triangle is \cfrac{1}{2} \, a b and the area of the smaller square is c^2.
There are two ways to find the area of the larger square.
- Combine the area of the four congruent triangles and the smaller square:
\begin{aligned}& =\cfrac{1}{2} \, a b+\cfrac{1}{2} \, a b+\cfrac{1}{2} \, a b+\cfrac{1}{2} \, a b+c^2 \\\\ & =2 a b+c^2\end{aligned} - Multiply the side lengths of the larger square together:
\begin{aligned}& =(a+b)(a+b) \\\\ & =a^2+2 a b+b^2\end{aligned}
Now set the two expressions equal to each other to prove a^2+b^2=c^2 \text{:}
\begin{aligned}a^2 +2 a b+b^2 &=2 a b+c^2 \\\\ -2 a b \hspace{0.3cm} & \hspace{0.3cm} -2 a b \\\\ a^2+b^2&=c^2\end{aligned}
Since the triangles formed by the vertices of a square will also be right triangles, the proof above shows that a^2+b^2=c^2 will always be true for the sides of a right triangle.
![[FREE] Pythagorean Theorem Worksheet (Grades 8)](https://thirdspacelearning.com/wp-content/uploads/2023/10/common-core-practice-tests.png)
[FREE] Pythagorean Theorem Worksheet (Grades 8)
![[FREE] Pythagorean Theorem Worksheet (Grades 8)](https://thirdspacelearning.com/wp-content/uploads/2023/10/common-core-practice-tests.png)
Use this quiz to check your grade 8 students’ understanding of pythagorean theorem. 15+ questions with answers covering a range of 8th grade topics on pythagorean theorem to identify areas of strength and support!
DOWNLOAD FREE![[FREE] Pythagorean Theorem Worksheet (Grades 8)](https://thirdspacelearning.com/wp-content/uploads/2023/10/common-core-practice-tests.png)
[FREE] Pythagorean Theorem Worksheet (Grades 8)
![[FREE] Pythagorean Theorem Worksheet (Grades 8)](https://thirdspacelearning.com/wp-content/uploads/2023/10/common-core-practice-tests.png)
Use this quiz to check your grade 8 students’ understanding of pythagorean theorem. 15+ questions with answers covering a range of 8th grade topics on pythagorean theorem to identify areas of strength and support!
DOWNLOAD FREE3D Pythagorean Theorem
You can find the length AG in the cuboid ABCDEFGH using the Pythagorean Theorem.
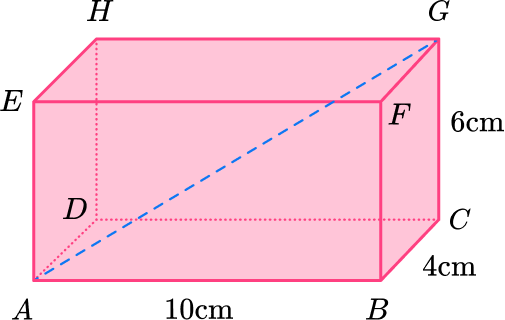
You can make a right triangle ACG which you can use to calculate AG.
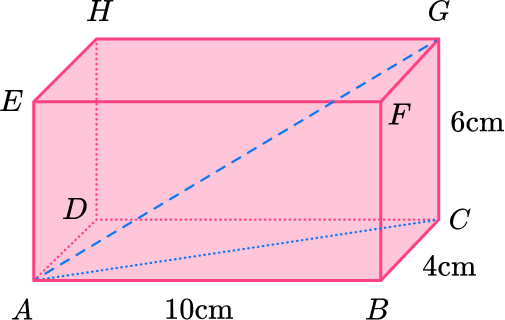
In order to use Pythagoras’ Theorem, you need to know two sides of the triangle. So in order to figure out the longest side AG, you first need to figure out one of the shorter sides AC.
Let’s call this side x and redraw this triangle.

You can see that the side labeled x forms the diagonal line of the base of the rectangular prism.

Triangle ABC is a right triangle, so we can use the Pythagorean Theorem to calculate x.
x=\sqrt{10^2 + 4^2} = 2\sqrt{29} = 10.7703…
So,
AG=\sqrt{10.7703…^2 + 6^2} = \sqrt{152}=2\sqrt{38} = 12.328…
So the required length is 12.4 \, cm (rounded to the nearest tenth).
Step-by-step guide: 3D Pythagorean Theorem
What is the Pythagorean Theorem?

Common Core State Standards
How does this relate to 8 th grade math?
- Grade 8 – Geometry (8.G.B.6)
Explain a proof of the Pythagorean Theorem and its converse.
- Grade 8 – Geometry (8.G.B.7)
Apply the Pythagorean Theorem to determine unknown side lengths in right triangles in real-world and mathematical problems in two and three dimensions.
How to use Pythagorean Theorem
In order to use Pythagorean Theorem:
- Label the sides of the triangle.
- Write down the formula and apply the numbers.
- Record the answer.
Pythagorean Theorem examples
Example 1: missing length of the hypotenuse c
Find x and answer to the nearest hundredth.
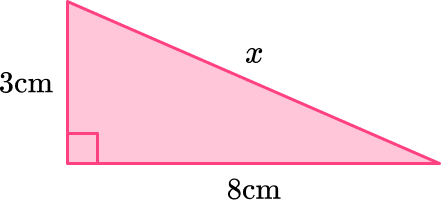
- Label the sides of the triangle.
Label the hypotenuse (the longest side) with c. The adjacent sides, next to the right angle can be labeled a and b (either way – they are interchangeable).
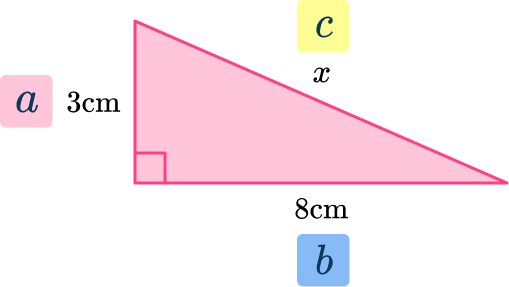
2Write down the formula and apply the numbers.
\begin{aligned}& a^2+b^2=c^2 \\\\ & 3^2+8^2=x^2 \\\\ & 9+64=x^2 \\\\ & 73=x^2 \\\\ & \sqrt{73}=x\end{aligned}
An alternative method of rearranging the formula and to put one calculation into a calculator will also work.
\begin{aligned}& a^2+b^2=c^2 \\\\ & c^2=a^2+b^2 \\\\ & c=\sqrt{a^2+b^2} \\\\ & x=\sqrt{3^2+8^2}\end{aligned}
3Record the answer.
Make sure you give your final answer in the correct form by calculating the square root value, including units where appropriate.
x=\sqrt{73}=8.5440037…
The final answer to the nearest hundredth is:
x=8.54 \mathrm{~cm}
Example 2: missing length c
Find x and answer to the nearest tenth.
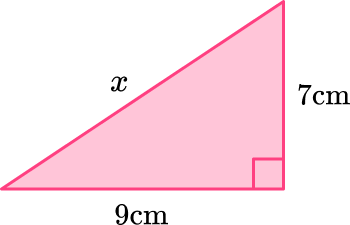
Label the sides of the triangle.
Label the hypotenuse (the longest side) with c. The adjacent sides, next to the right angle can be labeled a and b (either way – they are interchangeable).
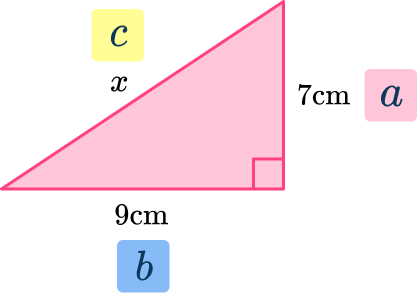
Write down the formula and apply the numbers.
\begin{aligned}& a^2 + b^2 = c^2 \\\\ & 7^2 + 9^2 = x^2 \\\\ & x^2 = 7^2 + 9^2 \\\\ & x^2 = 49+81 \\\\ & x^2 = 130 \\\\ & x = \sqrt{130}\end{aligned}
An alternative method is to rearrange the formula and put one calculation into a calculator.
\begin{aligned}& a^2+b^2=c^2 \\\\
& c^2=a^2+b^2 \\\\
& c=\sqrt{a^2+b^2} \\\\
& x=\sqrt{7^2+9^2}\end{aligned}
Record the answer.
Make sure you give your final answer in the correct form; including units where appropriate.
x=\sqrt{130}=11.40175.…
The final answer to the nearest tenth is:
x=11.4 \mathrm{~cm}
Example 3: finding an adjacent side (a short side)
Find x and write your answer to the nearest hundredth.
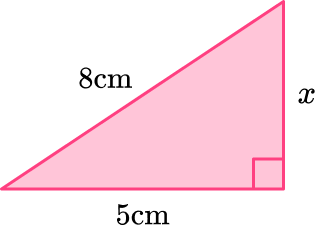
Label the sides of the triangle.
Label the hypotenuse (the longest side) with c. The adjacent sides, next to the right angle can be labeled a and b (either way – they are interchangeable).
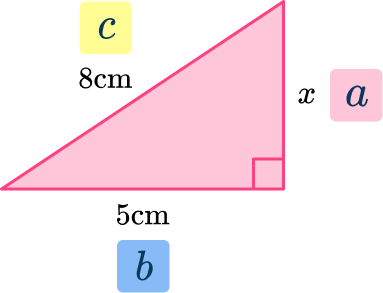
Write down the formula and apply the numbers.
\begin{aligned} & a^2 + b^2 = c^2 \\\\ & x^2 + 5^2 = 8^2 \\\\ & x^2+25 = 64 \\\\ & x^2 = 64 - 25 \\\\ & x^2 = 39 \\\\ & x =\sqrt{39}\ \end{aligned}
An alternative method is to rearrange the formula and put one calculation into a calculator.
\begin{aligned}& a^2+b^2=c^2 \\\\
& a^2=c^2-b^2 \\\\
& a=\sqrt{c^2-b^2} \\\\
& x=\sqrt{8^2-5^2}\end{aligned}
Record the answer.
Make sure you give your final answer in the correct form, including units where appropriate.
x=\sqrt{39}=6.244997.…
The final answer to the nearest hundredth is:
x=6.24 \mathrm{~cm}
Example 4: finding an adjacent side (a short side)
Find x and write your answer to the nearest tenth.

Label the sides of the triangle.
Label the hypotenuse (the longest side) with c. The adjacent sides, next to the right angle can be labeled a and b (either way – they are interchangeable).
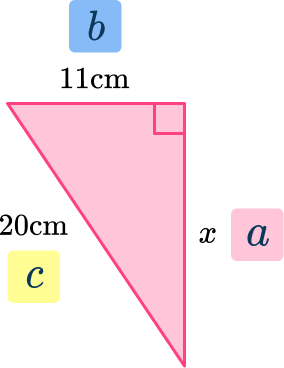
Write down the formula and apply the numbers.
\begin{aligned} & a^2 + b^2 = c^2 \\\\ & x^2 + 11^2 = 20^2\\\\ & x^2+121 = 400 \\\\ & x^2= 400 - 121 \\\\ & x^2 = 279\\\\ & x =\sqrt{279}\end{aligned}
An alternative method is to rearrange the formula and put one calculation into a calculator.
\begin{aligned}& a^2+b^2=c^2 \\\\
& a^2=c^2-b^2 \\\\
& a=\sqrt{c^2-b^2} \\\\
& x=\sqrt{20^2-11^2}\end{aligned}
Record the answer.
Make sure you give your final answer in the correct form; including units where appropriate.
x=\sqrt{279}=16.70329.…
The final answer rounded to the nearest tenth is:
x=16.7 \mathrm{~cm}
Example 5: checking if a triangle has a right angle
Is the triangle below a right triangle?
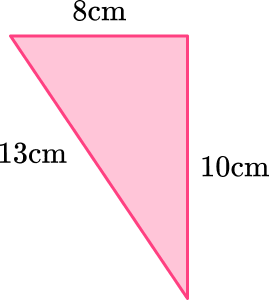
Label the sides of the triangle.
Label the longest side with c. The adjacent sides, next to the right angle can be labeled a and b (either way – they are interchangeable).
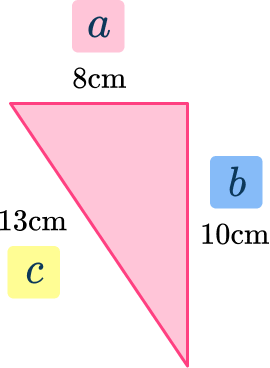
Write down the formula and apply the numbers.
\begin{aligned} & a^2 + b^2 = c^2 \\\\ & 8^2 + 10^2 = 13^2 \\\\ & 64+100 = 169 \\\\ & 164 = 169\end{aligned}
But this is NOT correct. Pythagorean Theorem only works with right triangles.
Record the answer.
Because 8^2 + 10^2
Example 6: checking if a triangle has a right angle
Is the triangle below a right triangle?

Label the sides of the triangle.
Label the longest side with c. The adjacent sides, next to the right angle can be labeled a and b (either way – they are interchangeable).
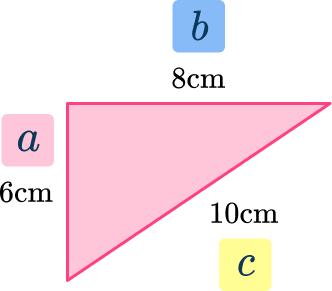
Write down the formula and apply the numbers.
\begin{aligned}& a^2 + b^2 = c^2 \\\\ & 6^2 + 8^2 = 10^2 \\\\ & 36+64 = 100 \\\\ & 100 = 100\end{aligned}
This is correct. Pythagorean Theorem only works with right triangles.
Record the answer.
Because 6^2 + 8^2 = 10^2 , the sides of the triangles fit with Pythagorean Theorem. Therefore, the triangle is a right triangle and c is a hypotenuse.
Teaching tips for Pythagorean Theorem
- In the beginning, give examples that are on grids and have the sides of the right triangle as positive integers. This allows students to draw the corresponding square for each side of the triangle and test to see that a^2+b^2=c^2.
- Give students a chance to try and prove the Pythagorean Theorem on their own. Then give students examples of a few different theorems and challenge them to find the one that makes the most sense for them.
- The Pythagorean Theorem has connections outside of math classes. If time allows, students can explore the history of this theorem.
Easy mistakes to make
- Not correctly identifying the hypotenuse
It is very important to make sure that the hypotenuse, the long side, is correctly identified and labeled c.
- Forgetting that right triangles may be in different orientations
The triangles can be drawn in different orientations.
For example,
These are examples of the same right triangle ADB in different orientations.
- Thinking the lengths of sides can only be whole numbers
Lengths can be decimals, fractions or even irrational numbers such as, \sqrt{2}.
- Not knowing the Pythagorean theorem can also be applied to other shapes
An application of Pythagorean theorem is to extend it to work on other shapes such as a trapezoid.
- Rounding too early
If you need to use Pythagorean Theorem in a question with multiple steps, do not round until the very end of the question or you will lose accuracy. For example, you may need to find the height of a triangle, and then use that height to find its area.
Practice Pythagorean Theorem questions
1. Find side x. Give your answer to the nearest hundredth:





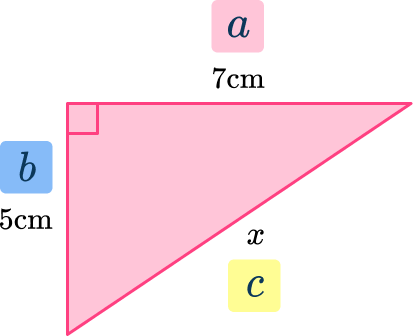
\begin{aligned}& a^2 + b^2 = c^2 \\\\ & 7^2 + 5^2 = x^2 \\\\ & x^2 = 7^2 + 5^2\\\\ & x^2 = 49+25 \\\\ & x^2 = 74 \\\\& x = \sqrt{74}\\\\ &x = 8.602325…\end{aligned}
x=8.60 \mathrm{~cm}
2. Find side x. Give your answer to the nearest hundredth:





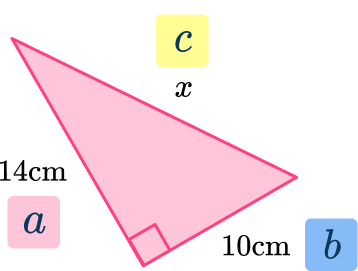
\begin{aligned}&a^2 + b^2 = c^2 \\\\ & 14^2 + 10^2 = x^2 \\\\ & x^2 = 14^2 + 10^2 \\\\ & x^2 = 196+10 \\\\ & x^2 = 296 \\\\ & x = \sqrt{296} \\\\ & x = 17.20465… \end{aligned}
x=17.20 \mathrm{~cm}
3. Find side x. Give your answer to the nearest hundredth:





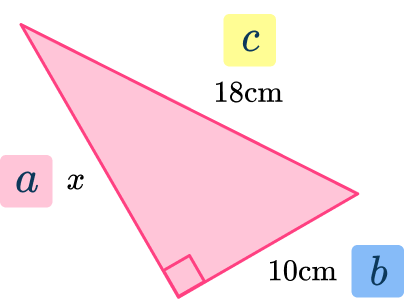
\begin{aligned}& a^2 + b^2 = c^2 \\\\ & x^2 + 10^2 = 18^2\\\\ & x^2+100 = 324 \\\\ & x^2 = 324 – 100 \\\\ & x^2 = 224 \\\\ & x =\sqrt{224} \\\\ & x = 14.96662…\end{aligned}
x=14.97 \mathrm{~cm}
4. Find side x. Give your answer to the nearest hundredth:





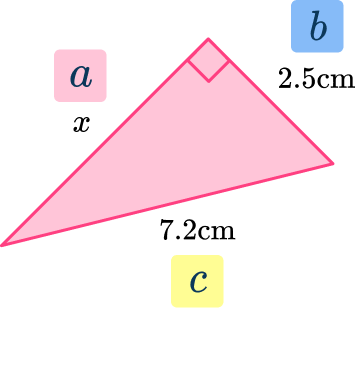
\begin{aligned}& a^2 + b^2 = c^2 \\\\ & x^2 + 2.5^2 = 7.2^2 \\\\ & x^2+6.25 = 51.84 \\\\ & x^2 = 51.84-6.25 \\\\ & x^2 = 45.59 \\\\ & x =\sqrt{45.59} \\\\ & x = 6.75203…\end{aligned}
x=6.75 \mathrm{~cm}
5. Is this a right triangle? Justify your answer with the Pythagorean Theorem.
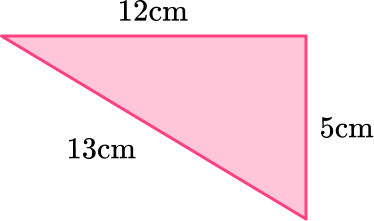
No, because 12^2+5^2 ≠ 13^2

Yes, because I measured the angle and it was 90^{\circ}

Yes, because 12^2+5^2=13^2

No, because I measured the angle and it was not 90^{\circ}

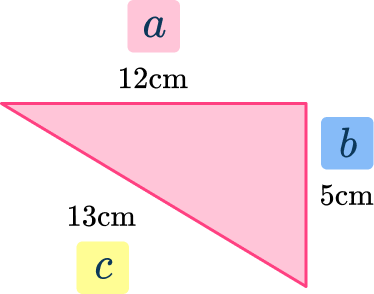
\begin{aligned}& a^2 + b^2 = c^2 \\\\ & 12^2 + 5^2 = 13^2 \\\\ & 144+25 = 169 \\\\ & 169 = 169 \end{aligned}
This is correct. Pythagorean Theorem only works with right triangles.
Therefore the triangle is a right triangle.
6. Is this a right triangle? Justify your answer with the Pythagorean Theorem.
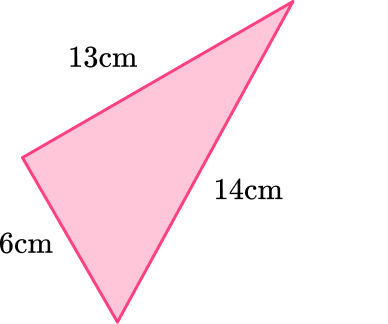
Yes, because 6^2+13^2=14^2

Yes, because I measured the angle and it was 90^{\circ}

No, because 6^2+13^2 ≠ 14^2

No, because I measured the angle and it was not 90^{\circ}

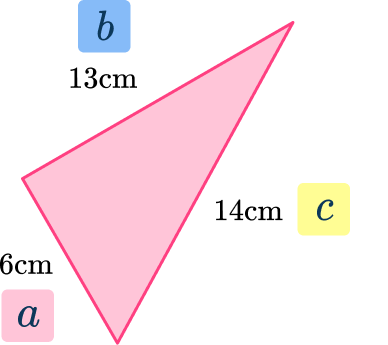
\begin{aligned}& a^2 + b^2 = c^2 \\\\ & 6^2 + 13^2 = 14^2 \\\\ & 36+169 = 196 \\\\ & 205 = 196\end{aligned}
This is NOT correct. Pythagorean Theorem only works with right triangles.
Therefore the triangle is NOT a right-angled triangle.
Pythagorean Theorem FAQs
Pythagorean Theorem is named after a Greek mathematician who lived about 2,500 years ago, however, the ancient Babylonians used this rule about 4 thousand years ago! At the same time, the Egyptians were using the theorem to help them with right angles when building structures.
No, this is only true for the sides of a right triangle. The sum of the squares of the lengths for a and b will only be equal to the square of side c if the triangle is right.
However, you can use this relationship to decide if a triangle is acute or obtuse. For an acute triangle, the square of the hypotenuse will be less than the sum of the squares of a and b. For an obtuse triangle, the square of the hypotenuse will be more than the sum of the squares of a and b.
Yes, there are many algebraic proofs and geometric proofs that address the Pythagorean Theorem. The proof shown at the top of this page is one of the simplest ways to prove the Pythagorean Theorem.
No, though they all follow the Pythagorean Theorem this does not mean they are similar. They are only similar if there is a multiplicative relationship between each corresponding side of the triangle.
The next lessons are
- Trigonometry
- Circle math
- Sectors, arcs and segments
Still stuck?
At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.
Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.

Find out how we can help your students achieve success with our math tutoring programs.
[FREE] Common Core Practice Tests (Grades 3 to 6)
Prepare for math tests in your state with these Grade 3 to Grade 6 practice assessments for Common Core and state equivalents.
40 multiple choice questions and detailed answers to support test prep, created by US math experts covering a range of topics!