High Impact Tutoring Built By Math Experts
Personalized standards-aligned one-on-one math tutoring for schools and districts
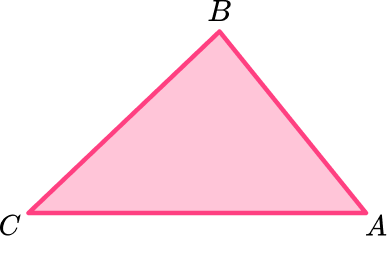
Right triangle
Here you will learn about right triangles, including what a right triangle is and how to solve problems with right triangles.
Students first learn about right triangles in the 4th grade with their work in geometry.
What is a right triangle?
A right triangle is a type of triangle that has one right angle ( 90^{\circ} angle).
The two sides of the triangle that meet at the right angle are perpendicular. In this case, side AB is perpendicular to side BC so angle B is 90^{\circ}.
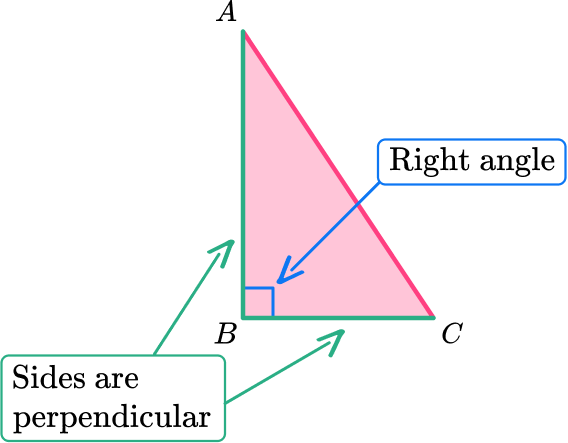
A right angle is 90^{\circ} and it is symbolized using a small square inside the angle at the vertex.
The longest side of the right triangle is called the hypotenuse. It is the side opposite to the right angle.

As you move into secondary school and study geometry, triangles are one of the most common shapes to recognize for angles in parallel lines, circle theorems, interior angles, trigonometry, Pythagoras’ theorem and many more.
![[FREE] Triangles Worksheet (Grade 4 to 5)](https://thirdspacelearning.com/wp-content/uploads/2023/07/Triangles-check-for-understanding-quiz-listing-image.png)
[FREE] Triangles Worksheet (Grade 4 to 5)
![[FREE] Triangles Worksheet (Grade 4 to 5)](https://thirdspacelearning.com/wp-content/uploads/2023/07/Triangles-check-for-understanding-quiz-listing-image.png)
Use this quiz to check your grade 4 to 5 students’ understanding of triangles. 10+ questions with answers covering a range of 4th and 5th grade triangle topics to identify areas of strength and support!
DOWNLOAD FREE![[FREE] Triangles Worksheet (Grade 4 to 5)](https://thirdspacelearning.com/wp-content/uploads/2023/07/Triangles-check-for-understanding-quiz-listing-image.png)
[FREE] Triangles Worksheet (Grade 4 to 5)
![[FREE] Triangles Worksheet (Grade 4 to 5)](https://thirdspacelearning.com/wp-content/uploads/2023/07/Triangles-check-for-understanding-quiz-listing-image.png)
Use this quiz to check your grade 4 to 5 students’ understanding of triangles. 10+ questions with answers covering a range of 4th and 5th grade triangle topics to identify areas of strength and support!
DOWNLOAD FREETypes of right triangles
There are two types of right triangles.
| Right isosceles triangle: | Scalene right triangle: |
|---|---|
● Two equal (congruent) sides  The equal angles are equal to 45^{\circ} each | ● No equal sides  |
What is a right triangle?
Common Core State Standards
How does this apply to 4th and 5th grade math?
- Grade 4 – Geometry (4.G.A.1)
Draw points, lines, line segments, rays, angles (right, acute, obtuse), and perpendicular and parallel lines. Identify these in two-dimensional figures.
- Grade 4 – Geometry (4.G.A.2)
Classify two-dimensional figures based on the presence or absence of parallel or perpendicular lines, or the presence or absence of angles of a specified size. Recognize right triangles as a category, and identify right triangles.
- Grade 5 – Geometry (5.G.B.3)
Understand that attributes belonging to a category of two-dimensional figures also belong to all subcategories of that category.
How to solve problems involving right angle triangles
In order to identify right triangles:
- Recall the definition.
- Explain how the triangle fits or does not fit the definition.
Right triangle examples
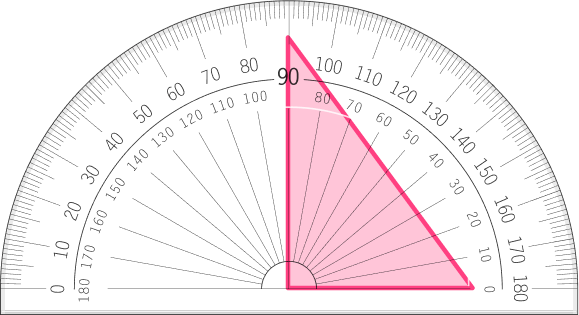
Example 1: identifying right triangles
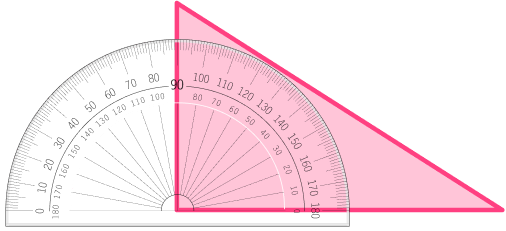
Is the triangle a right triangle?

- Recall the definition.
A right triangle has one right angle (90^{\circ}).
2Explain how the triangle fits or does not fit the definition.
There is one angle that appears to be 90^{\circ}. Measuring the angle on the protractor, it measures to be 90^{\circ}. So, the triangle is a right triangle.
Example 2: identifying right triangles
Is the triangle a right triangle?

Recall the definition.
A right triangle has one right angle (90^{\circ}).
Explain how the triangle fits or does not fit the definition.
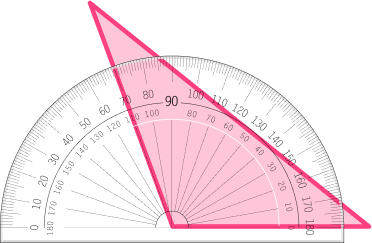
There does not appear to be any angle that looks 90^{\circ}. The angle looks obtuse and measures to be 110^{\circ}. The other two angles are acute. So the triangle is not a right triangle.
Example 3: identifying right triangles
Is triangle ABC a right triangle if side AB is perpendicular to side BC?
Recall the definition.
A right triangle has one right angle (90^{\circ}).
Perpendicular lines intersect (meet) to form a right angle.
Explain how the triangle fits or does not fit the definition.
Since AB and BC are perpendicular, a right angle (90^{\circ}) is formed at B.
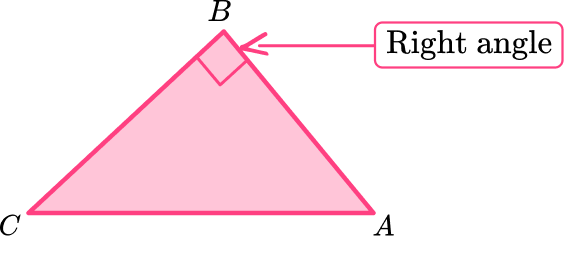
Triangle ABC is a right triangle.
Example 4: identifying right triangles
Ana drew a triangle where two of the sides of the triangle are perpendicular. Is the triangle Ana drew a right triangle?
Recall the definition.
A right triangle has one right angle (90^{\circ}).
Perpendicular lines intersect (meet) to form a right angle.
Explain how the triangle fits or does not fit the definition.
The triangle Ana drew is a right triangle because there is a right angle (90^{\circ}).
Example 5: identifying right triangles
Is the triangle below a right scalene triangle or a right isosceles triangle?
Recall the definition.
A scalene right triangle is a right triangle where the sides of a triangle have no equal sides and no equal angles.
Explain how the triangle fits or does not fit the definition.
The triangle has one right angle and three sides that have different measures. So, the right triangle is a right scalene triangle.
Example 6: identifying right triangles
Is the triangle below a right scalene triangle or a right isosceles triangle?

Recall the definition.
A right isosceles triangle is a right triangle with two equal sides and two equal angles.
Explain how the triangle fits or does not fit the definition.
The triangle has a right angle with two sides that are marked as equal and two angles that are marked as equal, so the triangle is a right isosceles triangle.
Teaching tips for right triangles
- Have students use manipulatives to investigate triangle properties.
- Facilitate learning opportunities like projects where students can see how right triangles are used in the real world.
- Integrate drawing activities where students can use rulers and protractors.
Easy mistakes to make
- Confusing angle facts
Make sure to recall that an acute angle is an angle greater than 0^{\circ} and less than 90^{\circ}; obtuse angle is an angle 90^{\circ} and less than 180^{\circ}; and a right angle is equal to 90^{\circ}.
- Thinking that if an angle looks like it’s \bf{90°} then it is a right angle
In geometry, the angle has to be marked as 90^{\circ} or you have to measure it to be 90^{\circ} to be certain that it is a right angle.
Related triangles lessons
Practice right triangle questions
1. Select the right triangle.








A right triangle is a triangle with a right angle. This triangle appears to have a right angle.
Measuring the angle with a protractor, you can see that it is 90^{\circ} which means the triangle is a right triangle.
2. Select the right isosceles triangle.
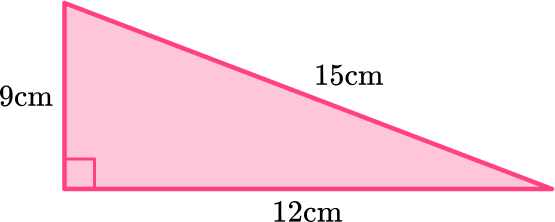







Right isosceles triangles have one right angle, two equal sides, and 2 equal angles.
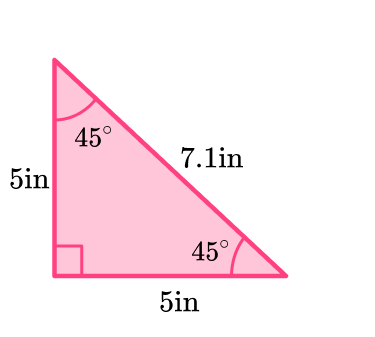
This triangle has a right angle, two angles that measure 45^{\circ} and two sides that measure 5 inches.
3. Which triangle has a set of perpendicular sides?








Perpendicular lines are lines that intersect (meet) at a right angle (90^{\circ}).
This triangle has two sides that are perpendicular because there is a square symbol that means 90^{\circ} at the vertex.

4. Which photo is a right triangle?






A right triangle has 1 right angle.
This triangle has three angles that are all acute, less than 90^{\circ}.
This triangle has three angles that are all acute, less than 90^{\circ}.
This triangle has an angle that is obtuse, greater than 90^{\circ} but less than 180^{\circ}.

This triangle is the right triangle because it has one 90^{\circ} angle.

5. Nora drew a triangle that has a pair of perpendicular sides. Which triangle could be the one Nora drew?








This is the triangle that Nora could have drawn because it’s the only triangle that has a right angle.
Perpendicular lines intersect to form right angles.

6. Which triangle represents a right scalene triangle?








A right scalene triangle is a triangle with no equal sides, no equal angles, and 1 right angle.
This triangle is a right triangle but there are two sides of the triangle marked as equal.

This triangle is the right scalene triangle because the sides have different measurements and there is one right angle.

Right triangle FAQs
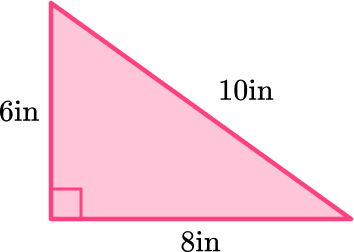
The Pythagorean theorem is a formula that shows the relationship of the side lengths of right triangles, a^2+b^2=c^2 where the sum of (side a ) ^2 and (side b ) ^2 is equal to (hypotenuse c ) ^2. (The sum of the squares of the sides is equal to the square of the hypotenuse.) You will learn how to use the Pythagorean theorem in 8th grade.
See also: Pythagorean Theorem
Trigonometry is the study of triangles. In trigonometry, you learn more about right triangles and the ratio of the sides of a right triangle – sine, cosine, and tangent. You will also learn about trigonometric functions.
A Pythagorean triple is composed of three positive integers that work in the Pythagorean theorem. For example, the numbers 3, 4, 5 are considered a Pythagorean triple because the sum of the squares of the sides is equal to the square of the 3^2+4^2=5^2 → 9+16 =25.
Special right triangles will be a topic you explore in high school. There are two special right triangles. The first one is an isosceles right triangle or 45-45-90 triangle. The other one is a scalene right triangle, or 30-60-90 triangle.
The way you find the area of a right triangle is the same way you find the area of oblique triangles. You can use the formula for the area of the triangle, A=\cfrac{1}{2} \, \cdot b \cdot h.
Angles can be measured in two different units, degrees or radians. You will learn how to measure angles in radians in high school.
You find the perimeter of a right triangle by adding up the length of the sides and the length of the hypotenuse, which is the largest side of the triangle.
Only right triangles have a side called the hypotenuse. The hypotenuse of a right triangle is the longest side of the triangle.
The next lessons are
Still stuck?
At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.
Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.

Find out how we can help your students achieve success with our math tutoring programs.
[FREE] Common Core Practice Tests (3rd to 8th Grade)
Prepare for math tests in your state with these 3rd Grade to 8th Grade practice assessments for Common Core and state equivalents.
Get your 6 multiple choice practice tests with detailed answers to support test prep, created by US math teachers for US math teachers!